2024-2025学年北师大版七年级数学下册课件 1.1幂的乘除(第4课时)同底数幂的除法(30张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册课件 1.1幂的乘除(第4课时)同底数幂的除法(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 722.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 00:00:00 | ||
图片预览









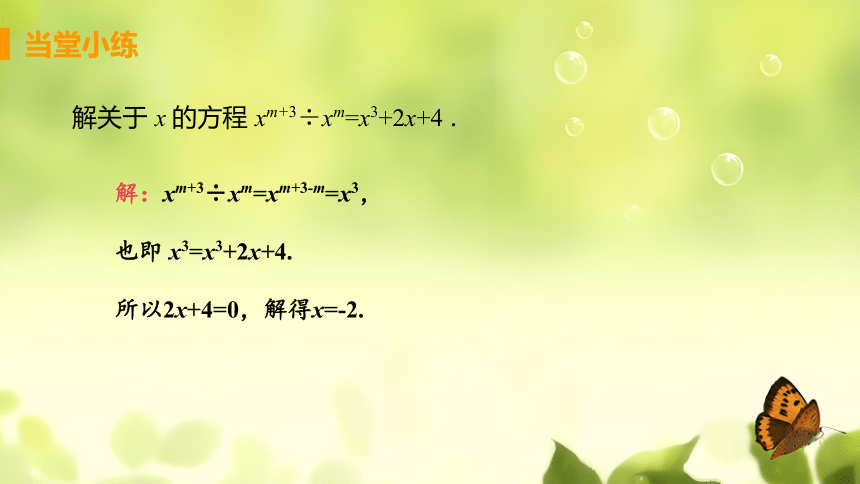
文档简介
(共30张PPT)
北师大版七年级数学下册课件
第一章 整式的乘除
1.1幂的乘除
课时4 同底数幂的除法
1.了解并掌握同底数幂的除法的运算法则.(重点)
2.掌握同底数幂的除法的运算法则的推导以及零指数幂 的意义(难点)
学习目标
新课讲解
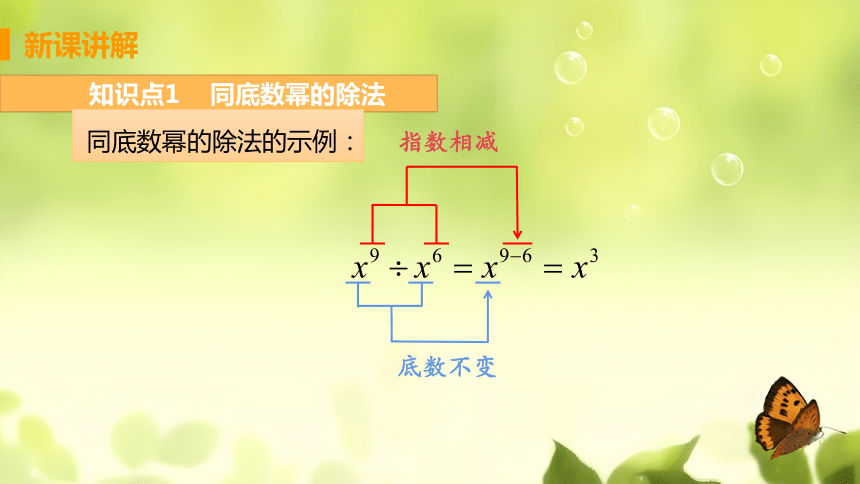
知识点1 同底数幂的除法
性质:同底数幂相除,底数不变,指数相减.
符号表示:am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
(1) 底数 a 可以是单项式,也可以是多项式,但不可以是 0;
(2) 同底数幂相除,底数不变,指数是相减而不是相除.
新课讲解
知识点1 同底数幂的除法
同底数幂的除法的示例:
底数不变
指数相减
新课讲解
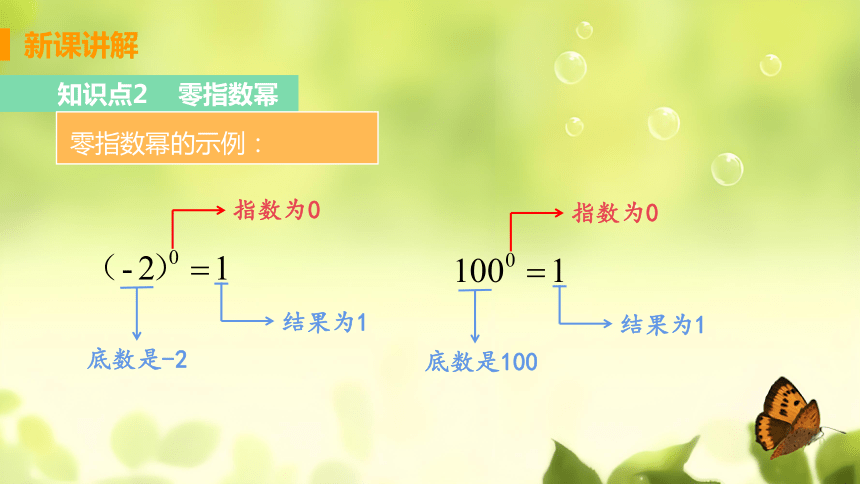
知识点2 零指数幂
性质:任何不等于0的数的零次幂都等于1.
符号表示:a0=1(a≠0).
(1) 零指数幂中的底数可以是单项式,也可以是多项式,但不可以是0;
(2) 因为 a=0 时,a0 无意义,所以 a0 有意义的条件是 a≠0,常据此确定底数中所含字母的取值范围.
新课讲解
知识点2 零指数幂
零指数幂的示例:
底数是-2
指数为0
结果为1
底数是100
指数为0
结果为1
新课讲解
知识点2 零指数幂
a0 =1 (a≠0)的推导过程:
当 m=n 时,am ÷an=am-n =a0 ,
因为 m=n ,
所以am ÷an =1 .
则 a0 =1 .
拓 展
新课讲解
3
B
解析:(-a)3÷a=-a3÷a=-a3-1=-a2 .
要注意a的指数为1,计算的时候不要遗漏.
计算:(-a)3÷a 结果正确的是( )
A. a2 B. -a2 C. -a3 D. -a4
课堂小结
同底数幂的除法
同底数幂的除法的运算法则
零指数幂的意义
当堂小练
2.计算16m÷4n÷2等于( )
A.2m-n-1
B.22m-n-1
C.23m-2n-1
D.24m-2n-1
D
分析:因为16=24,所以16m=24m,
因为4=22,所以4n=22n
所以原式=24m÷22n÷21=24m-2n-1
当堂小练
解关于 x 的方程 xm+3÷xm=x3+2x+4 .
解:xm+3÷xm=xm+3-m=x3,
也即 x3=x3+2x+4.
所以2x+4=0,解得x=-2.
拓展与延伸
若 (1-x)1-3x=1,则 x 的取值有( )
A.0个 B.1个 C.2个 D.3个
C
解析:根据零指数幂的意义可知:当1-3x=0且1-x≠0时,
(1-x)1-3x=1,此时 .
根据1的任意次幂仍然为1可知:当1-x=1时, (1-x)1-3x=1.此时x=0.
则满足条件的 x 的值有2个.
(1)探究:用你熟悉的方法计算,从这些计算结果中你能发现什么规律?
①25÷22= ;②107÷103= ;
③a7÷a3= (a≠0).
同底数幂相除,底数 ,指数 .
知识点 1
同底数幂的除法法则
23
104
a4
不变
相减
(2)同底数幂的除法:
am÷an===a( ).
其中a≠0,m,n都是正整数,且m>n.
m-n
1.计算:
(1)a8÷a3= ;
(2)(-a)10÷(-a)3= ;
(3)x11÷x6= ;
(4)x3n+1÷xn+1= ;
(5)(2x)5÷(2x)2= ;
(6)(2a)7÷(2a)4.
解:原式=(2a)7-4=(2a)3=8a3.
a5
-a7
x5
x2n
8x3
思考:当m=n或m(1)因为am ÷ am=1,am ÷ am=a( )=a( ),
所以可以得到a0= (其中a 0).
规定1:当a≠0时,a0= ,即:任何不等于0的数的0次幂都等于
.
(2)规定2:任何不等于0的数的-p次幂,等于这个数的p次幂的倒数.用公式表示为a-p= (a≠0,p是正整数).
知识点 2
零指数幂和负整数指数幂
m-m
0
1
≠
1
1
2.计算:
(1)= ;
(2)(-3)0= ;
(3)π0= ;
(4)100= ;
(5)3-2= ;
(6)70×(-2)-3= .
1
1
1
1
-
(1)一般地,一个小于1的正数可以表示为 ,其中1≤a<10,n是 ,且n的绝对值等于原数的左边第一个非零数字前零的个数(包括小数点前面的零).
归纳:用科学记数法表示一个数,先确定a的值,再确定n的值.例如:0.000 001=1×10-6;
(2)还原科学记数法表示的数:把a×10n形式的数(n为负整数)写成小数的形式时,a的小数点应向左移动|n|位.例如:3×10-6=0.000 003.
知识点 3
用科学记数法表示小于1的正数
a×10n
负整数
3.(1)计算:①10-3= ;
②0.000 1==10( ).
(2)用科学记数法表示下列各数:
①0.006 358= ;
②0.000 033 4= ;
③0.000 000 063 2= .
4.将6.18×10-3化为小数是( )
A.0.000 618 B.0.006 18 C.0.061 8 D.0.618
0.001
-4
6.358×10-3
3.34×10-5
6.32×10-8
B
10.(人教8上P104改编)计算:
(1)(ab)5÷(ab)2= ;
(2)(-x)5÷(-x)= ;
(3)72m+1÷7m= ;
(4)(xy2)5÷(xy2)4= ;
(5)(a-1)0= (其中a≠1).
a3b3
x4
7m+1
xy2
1
6.【例2】计算:
(1)(-4)-2÷(-4)5;
(2)÷.
解: (1)原式=(-4)-2-5=(-4)-7= .
解: (2)原式=.
11.计算:2-1+(3.14-π)0-23+.
解:原式= .
12.计算:(a-b)3÷(a-b)-2·(a-b)4.
解:原式=(a-b)3-(-2)·(a-b)4
=(a-b)3+2+4=(a-b)9.
8.(跨学科融合)(2024大庆)人体内一种细胞的直径约为1.56微米,相当于0.000 001 56米,数字0.000 001 56用科学记数法表示为( )
A.1.56×10-5 B.0.156×10-5
C.1.56×10-6 D.15.6×10-7
C
13.下列是用科学记数法表示的数,用小数把它们表示出来:
(1)3.35×10-5= ;
(2)8.2×10-4= ;
(3)空气的密度是1.293×10-3 g/cm3,1.293×10-3= (用小数表示).
0.000 033 5
0.000 82
0.001 293
9.【例5】已知am=3,an=5,求am-n的值.
解:am-n=am ÷ an=3÷5= .
★14. (应用意识)已知10x=20,10y=5-1,求9x÷32y的值.
0.50
解:因为10x=20,10y=5-1= ,
所以10x÷10y=10x-y=20÷=100=102.
所以x-y=2.
所以9x÷32y=9x÷9y=9x-y=92=81.
布置作业
请完成课后对应习题
THANKS
北师大版七年级数学下册课件
第一章 整式的乘除
1.1幂的乘除
课时4 同底数幂的除法
1.了解并掌握同底数幂的除法的运算法则.(重点)
2.掌握同底数幂的除法的运算法则的推导以及零指数幂 的意义(难点)
学习目标
新课讲解
知识点1 同底数幂的除法
性质:同底数幂相除,底数不变,指数相减.
符号表示:am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
(1) 底数 a 可以是单项式,也可以是多项式,但不可以是 0;
(2) 同底数幂相除,底数不变,指数是相减而不是相除.
新课讲解
知识点1 同底数幂的除法
同底数幂的除法的示例:
底数不变
指数相减
新课讲解
知识点2 零指数幂
性质:任何不等于0的数的零次幂都等于1.
符号表示:a0=1(a≠0).
(1) 零指数幂中的底数可以是单项式,也可以是多项式,但不可以是0;
(2) 因为 a=0 时,a0 无意义,所以 a0 有意义的条件是 a≠0,常据此确定底数中所含字母的取值范围.
新课讲解
知识点2 零指数幂
零指数幂的示例:
底数是-2
指数为0
结果为1
底数是100
指数为0
结果为1
新课讲解
知识点2 零指数幂
a0 =1 (a≠0)的推导过程:
当 m=n 时,am ÷an=am-n =a0 ,
因为 m=n ,
所以am ÷an =1 .
则 a0 =1 .
拓 展
新课讲解
3
B
解析:(-a)3÷a=-a3÷a=-a3-1=-a2 .
要注意a的指数为1,计算的时候不要遗漏.
计算:(-a)3÷a 结果正确的是( )
A. a2 B. -a2 C. -a3 D. -a4
课堂小结
同底数幂的除法
同底数幂的除法的运算法则
零指数幂的意义
当堂小练
2.计算16m÷4n÷2等于( )
A.2m-n-1
B.22m-n-1
C.23m-2n-1
D.24m-2n-1
D
分析:因为16=24,所以16m=24m,
因为4=22,所以4n=22n
所以原式=24m÷22n÷21=24m-2n-1
当堂小练
解关于 x 的方程 xm+3÷xm=x3+2x+4 .
解:xm+3÷xm=xm+3-m=x3,
也即 x3=x3+2x+4.
所以2x+4=0,解得x=-2.
拓展与延伸
若 (1-x)1-3x=1,则 x 的取值有( )
A.0个 B.1个 C.2个 D.3个
C
解析:根据零指数幂的意义可知:当1-3x=0且1-x≠0时,
(1-x)1-3x=1,此时 .
根据1的任意次幂仍然为1可知:当1-x=1时, (1-x)1-3x=1.此时x=0.
则满足条件的 x 的值有2个.
(1)探究:用你熟悉的方法计算,从这些计算结果中你能发现什么规律?
①25÷22= ;②107÷103= ;
③a7÷a3= (a≠0).
同底数幂相除,底数 ,指数 .
知识点 1
同底数幂的除法法则
23
104
a4
不变
相减
(2)同底数幂的除法:
am÷an===a( ).
其中a≠0,m,n都是正整数,且m>n.
m-n
1.计算:
(1)a8÷a3= ;
(2)(-a)10÷(-a)3= ;
(3)x11÷x6= ;
(4)x3n+1÷xn+1= ;
(5)(2x)5÷(2x)2= ;
(6)(2a)7÷(2a)4.
解:原式=(2a)7-4=(2a)3=8a3.
a5
-a7
x5
x2n
8x3
思考:当m=n或m
所以可以得到a0= (其中a 0).
规定1:当a≠0时,a0= ,即:任何不等于0的数的0次幂都等于
.
(2)规定2:任何不等于0的数的-p次幂,等于这个数的p次幂的倒数.用公式表示为a-p= (a≠0,p是正整数).
知识点 2
零指数幂和负整数指数幂
m-m
0
1
≠
1
1
2.计算:
(1)= ;
(2)(-3)0= ;
(3)π0= ;
(4)100= ;
(5)3-2= ;
(6)70×(-2)-3= .
1
1
1
1
-
(1)一般地,一个小于1的正数可以表示为 ,其中1≤a<10,n是 ,且n的绝对值等于原数的左边第一个非零数字前零的个数(包括小数点前面的零).
归纳:用科学记数法表示一个数,先确定a的值,再确定n的值.例如:0.000 001=1×10-6;
(2)还原科学记数法表示的数:把a×10n形式的数(n为负整数)写成小数的形式时,a的小数点应向左移动|n|位.例如:3×10-6=0.000 003.
知识点 3
用科学记数法表示小于1的正数
a×10n
负整数
3.(1)计算:①10-3= ;
②0.000 1==10( ).
(2)用科学记数法表示下列各数:
①0.006 358= ;
②0.000 033 4= ;
③0.000 000 063 2= .
4.将6.18×10-3化为小数是( )
A.0.000 618 B.0.006 18 C.0.061 8 D.0.618
0.001
-4
6.358×10-3
3.34×10-5
6.32×10-8
B
10.(人教8上P104改编)计算:
(1)(ab)5÷(ab)2= ;
(2)(-x)5÷(-x)= ;
(3)72m+1÷7m= ;
(4)(xy2)5÷(xy2)4= ;
(5)(a-1)0= (其中a≠1).
a3b3
x4
7m+1
xy2
1
6.【例2】计算:
(1)(-4)-2÷(-4)5;
(2)÷.
解: (1)原式=(-4)-2-5=(-4)-7= .
解: (2)原式=.
11.计算:2-1+(3.14-π)0-23+.
解:原式= .
12.计算:(a-b)3÷(a-b)-2·(a-b)4.
解:原式=(a-b)3-(-2)·(a-b)4
=(a-b)3+2+4=(a-b)9.
8.(跨学科融合)(2024大庆)人体内一种细胞的直径约为1.56微米,相当于0.000 001 56米,数字0.000 001 56用科学记数法表示为( )
A.1.56×10-5 B.0.156×10-5
C.1.56×10-6 D.15.6×10-7
C
13.下列是用科学记数法表示的数,用小数把它们表示出来:
(1)3.35×10-5= ;
(2)8.2×10-4= ;
(3)空气的密度是1.293×10-3 g/cm3,1.293×10-3= (用小数表示).
0.000 033 5
0.000 82
0.001 293
9.【例5】已知am=3,an=5,求am-n的值.
解:am-n=am ÷ an=3÷5= .
★14. (应用意识)已知10x=20,10y=5-1,求9x÷32y的值.
0.50
解:因为10x=20,10y=5-1= ,
所以10x÷10y=10x-y=20÷=100=102.
所以x-y=2.
所以9x÷32y=9x÷9y=9x-y=92=81.
布置作业
请完成课后对应习题
THANKS
同课章节目录
