初中数学华师大版九年级下册 27.1.2 圆的对称性—弦、弧、圆心角 课件(第一课时)(23张PPT)
文档属性
| 名称 | 初中数学华师大版九年级下册 27.1.2 圆的对称性—弦、弧、圆心角 课件(第一课时)(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 18:13:06 | ||
图片预览






文档简介
(共23张PPT)
(第一课时)弦、弧、圆心角
27.1.2:圆的对称性
学习目标
1.理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.(难点)
复习回顾
连接圆上任意两点间的线段叫做弦。
直径是最长的弦
连接圆上任意两点间的部分叫做弧。
同圆或等圆中,能够完全重合的弧。
大于半圆的弧。
小于半圆的弧。
弦:
弧:
等弧:
特殊弦:
优弧:
劣弧:
知识精讲:
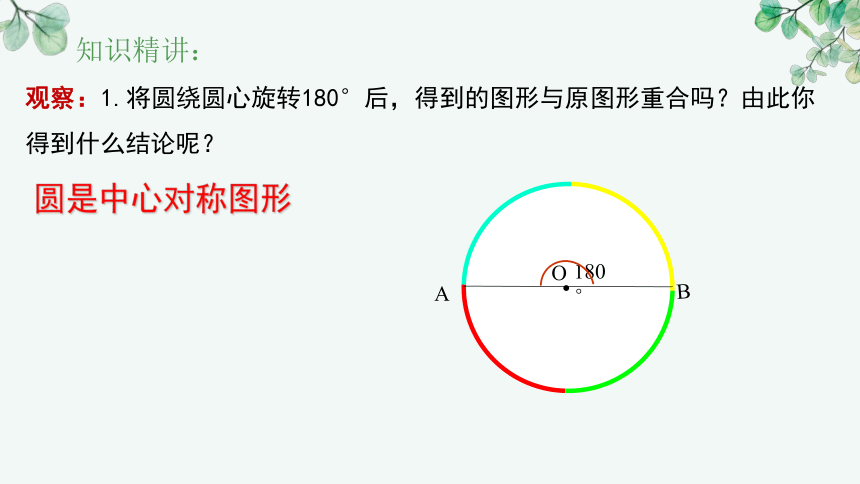
观察:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
圆是中心对称图形
知识精讲:
2.把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
·
O
α
圆是旋转对称图形,具有旋转不变性
圆的旋转不变性总结:
1.圆是中心对称图形,圆心就
是它的对称中心.
2.圆具有旋转不变性,把圆
绕圆心旋转任意一个角度,
所得的图形都与原图形重合.
O
α
·
O
B
A
·
O
B
A
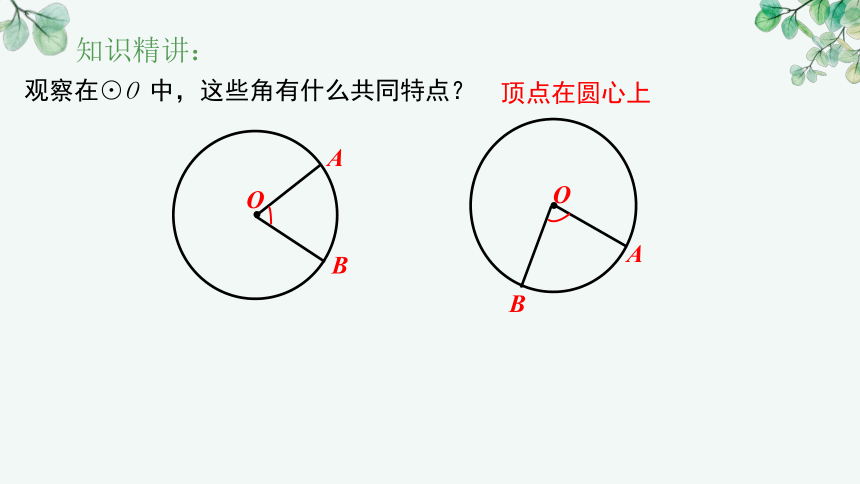
观察在⊙O 中,这些角有什么共同特点?
顶点在圆心上
知识精讲:
O
A
B
M
1.圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
2.圆心角 ∠AOB 所对的弧为 AB.
⌒
弦
圆心角及相关概念总结:
知识精讲:
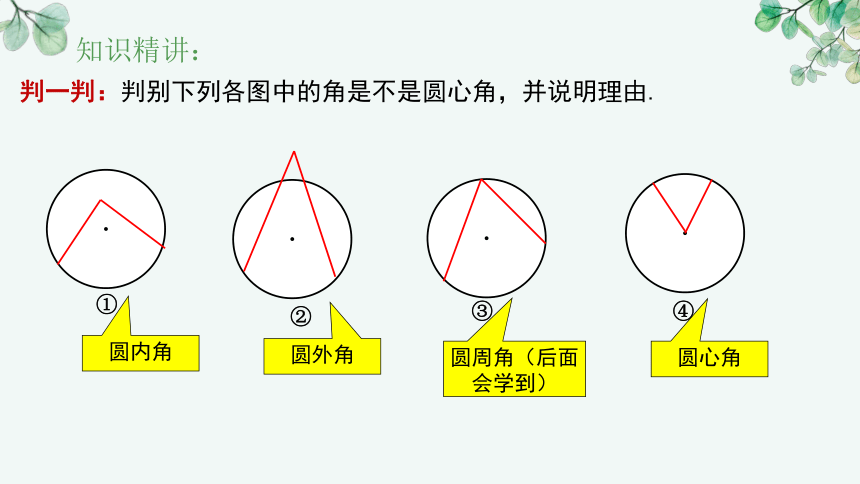
判一判:判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
圆内角
圆外角
圆周角(后面会学到)
圆心角
知识精讲:
在同圆中探究
C
·
O
A
B
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB = 弦CD
在⊙O中,如果∠AOB = ∠COD,那么, 与 ,弦 AB 与弦 CD 有怎样的数量关系?
知识精讲:
在同一个圆中,如果圆心角相等,那么它们所对弧相等,所对的弦相等.
①∠AOB = ∠COD
③AB = CD
要点归纳
弧、弦与圆心角的关系定理
A
B
O
D
C
②
思考 定理“在同圆或等圆中,如果圆心角相等,那么它们所对弧相等,所对的弦相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
在同圆或等圆中
题设
结论
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
要点归纳
关系结构图
温馨提示:一条弦对应两条弧,由弦相等得到弧相等时需要区分优弧和劣弧.
在同圆或等圆中
弧、弦、圆心角之间关系定理的推论
在同一个圆中,如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同一个圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
(3) 圆心角相等,所对的弦相等. ( )
(2) 等弧所对的弦相等. ( )
(1) 等弦所对的弧相等. ( )
×
×
√
判断正误:
辨一辨
1.【中考 枣庄】下列图形,可以看成中心对称图形的是( )
B
针对性练习
2.下列关于圆的轴对称性的说法:
①每条直径所在的直线都是圆的对称轴;
②每条半径所在的直线都是圆的对称轴;
③过圆心的每条直线都是圆的对称轴;
④过直径上任意一点的直线都是圆的对称轴.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
C
3.如图,下列各角是圆心角的是( )
A.∠ABC
B.∠AOB
C.∠OAB
D.∠OCB
B
4.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD的度数为( )
A.25°
B.30°
C.50°
D.65°
C
︵
B
5.在同圆或等圆中,不一定成立的是( )
A.相等的圆心角所对的弧相等
B.相等的弦所对的弧相等
C.相等的弧所对的弦相等
D.相等的弧所对的圆心角相等
证明:
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
6. 如图,在⊙O中, AB=AC ,∠ACB=60°,求证:∠AOB=∠BOC=
∠AOC.
·
A
B
C
O
⌒ ⌒
∵AB=CD,
⌒ ⌒
谢谢学习!
(第一课时)弦、弧、圆心角
27.1.2:圆的对称性
学习目标
1.理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.(难点)
复习回顾
连接圆上任意两点间的线段叫做弦。
直径是最长的弦
连接圆上任意两点间的部分叫做弧。
同圆或等圆中,能够完全重合的弧。
大于半圆的弧。
小于半圆的弧。
弦:
弧:
等弧:
特殊弦:
优弧:
劣弧:
知识精讲:
观察:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
圆是中心对称图形
知识精讲:
2.把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
·
O
α
圆是旋转对称图形,具有旋转不变性
圆的旋转不变性总结:
1.圆是中心对称图形,圆心就
是它的对称中心.
2.圆具有旋转不变性,把圆
绕圆心旋转任意一个角度,
所得的图形都与原图形重合.
O
α
·
O
B
A
·
O
B
A
观察在⊙O 中,这些角有什么共同特点?
顶点在圆心上
知识精讲:
O
A
B
M
1.圆心角:顶点在圆心的角,叫圆心角,如∠AOB .
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角,对应出现三个量:
圆心角
弧
2.圆心角 ∠AOB 所对的弧为 AB.
⌒
弦
圆心角及相关概念总结:
知识精讲:
判一判:判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
圆内角
圆外角
圆周角(后面会学到)
圆心角
知识精讲:
在同圆中探究
C
·
O
A
B
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB = 弦CD
在⊙O中,如果∠AOB = ∠COD,那么, 与 ,弦 AB 与弦 CD 有怎样的数量关系?
知识精讲:
在同一个圆中,如果圆心角相等,那么它们所对弧相等,所对的弦相等.
①∠AOB = ∠COD
③AB = CD
要点归纳
弧、弦与圆心角的关系定理
A
B
O
D
C
②
思考 定理“在同圆或等圆中,如果圆心角相等,那么它们所对弧相等,所对的弦相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
在同圆或等圆中
题设
结论
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
要点归纳
关系结构图
温馨提示:一条弦对应两条弧,由弦相等得到弧相等时需要区分优弧和劣弧.
在同圆或等圆中
弧、弦、圆心角之间关系定理的推论
在同一个圆中,如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同一个圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
(3) 圆心角相等,所对的弦相等. ( )
(2) 等弧所对的弦相等. ( )
(1) 等弦所对的弧相等. ( )
×
×
√
判断正误:
辨一辨
1.【中考 枣庄】下列图形,可以看成中心对称图形的是( )
B
针对性练习
2.下列关于圆的轴对称性的说法:
①每条直径所在的直线都是圆的对称轴;
②每条半径所在的直线都是圆的对称轴;
③过圆心的每条直线都是圆的对称轴;
④过直径上任意一点的直线都是圆的对称轴.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
C
3.如图,下列各角是圆心角的是( )
A.∠ABC
B.∠AOB
C.∠OAB
D.∠OCB
B
4.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD的度数为( )
A.25°
B.30°
C.50°
D.65°
C
︵
B
5.在同圆或等圆中,不一定成立的是( )
A.相等的圆心角所对的弧相等
B.相等的弦所对的弧相等
C.相等的弧所对的弦相等
D.相等的弧所对的圆心角相等
证明:
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
6. 如图,在⊙O中, AB=AC ,∠ACB=60°,求证:∠AOB=∠BOC=
∠AOC.
·
A
B
C
O
⌒ ⌒
∵AB=CD,
⌒ ⌒
谢谢学习!
