沪科版七下(2024版)第7章 小结与复习 课件
文档属性
| 名称 | 沪科版七下(2024版)第7章 小结与复习 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-25 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
第7章 一元一次不等式与不等式组
小结与复习
01
教学目标
02
知识体系
03
回顾与思考
04
自评与互评
05
课堂练习
06
作业布置
01
教学目标
复习巩固不等式的概念及不等式的基本性质。
01
复习巩固一元一次不等式及其不等式组的解法,能够准确求解并正确表示解集。
02
能够正确分析实际问题中的不等关系,建立相应的不等式模型,能够准确列出不等式并求解。
03
02
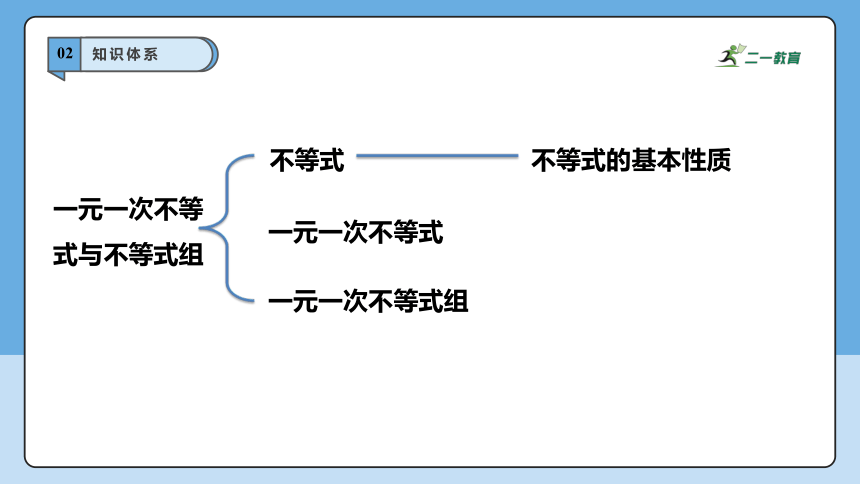
知识体系
一元一次不等式与不等式组
不等式
一元一次不等式组
一元一次不等式
不等式的基本性质
03
回顾与思考
1.不等式的基本性质:
(1)_______________________________________________;
(2)_______________________________________________;
(3)_______________________________________________;
(4)_______________________________________________;
(5)_______________________________________________.
如果,那么,.
如果,,那么,.
如果,,那么,.
如果,那么.
如果,,那么.
03
回顾与思考
2.解一元一次不等式,就是根据不等式的基本性质和运算律,通过________________、______________、_________________、 ___________________、___________________等步骤,将原不等式变形为不等式ax>b(a≠0)的形式,再在不等式两边同除以未知数的系数a,从而得到不等式的解集x_____________________(当a>0时)[或x__________________(当a<0时)].
去分母
去括号
移项
合并同类项
x系数化为1
>
<
03
回顾与思考
3.解不等式组是求不等式组_________________的过程。
假设a>b,
(1)不等式组的解集为_______________;
(2)不等式组的解集为_______________;
(3)不等式组的解集为_______________;
(4)不等式组的解集为_______________。
解集
无解
03
回顾与思考
4.不等式(组)是反映现实世界数量之间不等关系的一个数学模型,建立不等式(组)模型解决实际问题的关键是:
(1)分析问题中有哪些数量;
(2)分析这些数量间的关系;
(3)建立不等式(组)模型.
04
自评与互评
1.解一元一次不等式(组)过程中,有哪些需要注意的问题 与同学们分享.
去分母:需要两边同时乘以分母的最小公倍数。但此时要注意,如果乘以的数是负数,不等号的方向需要改变。
去括号:在去除括号时,要特别注意括号前的符号。如果括号前是负号,那么括号内的每一项都要变号。移项:移项要变号。
系数化为1:如果除以的数是负数,不等号的方向需要改变。
04
自评与互评
1.解一元一次不等式(组)过程中,有哪些需要注意的问题 与同学们分享.
解集:不等式组的解集是满足所有不等式的x的集合。因此,需要找出所有不等式的交集。
在实际问题中:不等式的解往往需要符合实际情况,因此需要对解进行检验,确保其满足问题的实际背景。
04
自评与互评
2.方程和不等式都是描述现实生活中数量关系的重要模型,你能说说两者的相同点与不同点吗
相同点
1.基础概念:方程和不等式都基于数学中的等式和不等式关系,用于表示变量之间的数量关系。
2.未知数:在方程和不等式中,都包含未知数(通常用字母表示),这些未知数需要通过求解过程来确定。
3.求解方法:方程和不等式的求解都涉及一系列的数学运算和推理过程,如移项、合并同类项、求解等。
04
自评与互评
2.方程和不等式都是描述现实生活中数量关系的重要模型,你能说说两者的相同点与不同点吗
不同点
1.定义:方程是一个等式,表示两个数学表达式相等;而不等式则是一个关系式,表示两个数学表达式之间的大小关系(大于、小于、大于等于、小于等于)。
2.解的个数:对于方程,通常有一个或多个解(在某些情况下可能无解),这些解满足等式关系;而对于不等式,解通常是一个解集,表示满足不等式关系的所有可能值。
04
自评与互评
2.方程和不等式都是描述现实生活中数量关系的重要模型,你能说说两者的相同点与不同点吗
不同点
3.求解过程:
在求解方程时,目标是找到使等式成立的未知数的值;而在求解不等式时,目标是找到满足不等式关系的未知数的取值范围。
05
课堂练习
【知识技能类作业】必做题:
1.下列说法中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.若关于的不等式组有且只有三个整数解,则的最大值是( )
A.3 B.4 C.5 D.6
C
C
05
课堂练习
【知识技能类作业】必做题:
3.解不等式的过程如下:①去分母,得;②去括号,得;③移项,合并同类项,得;④系数化为1,得.其中错误的一步是( )
A.① B.② C.③ D.④
D
05
课堂练习
【知识技能类作业】选做题:
4.若不等式x>y和(a-3)x<(a-3)y成立,则a的取值范围是 .
5.若是关于的一元一次不等式,则的值为 .
6.若关于的不等式组无解,则的取值范围是 .
2
05
课堂练习
7.已知,;,;都是关于x,y的二元一次方程的解.
(1)求a,b的值;
(2)当x为何值时,y的值小于0.
(1)解:∵,;,;都是关于x,y的二元一次方程的解,
故将,;,代入二元一次方程得: ,
解得: .
【综合拓展类作业】
05
课堂练习
(2)解:由(1)可知,
所以,
若要是y的值小于0,即 ,
解得:,
∴当时,y的值小于0.
【综合拓展类作业】
06
作业布置
【知识技能类作业】
1.现有下列各式:①-3<0;②x+3y≥0;③x=3;④x2+xy+y2.其中不等式有( )
A.1个 B.2个 C.3个 D.4个
2.关于的不等式组的最小整数解为1,则的取值范围是( )
A. B.
C. D.或
3.已知不等式的正整数解恰好是1、2、3,则的取值范围是______________.
B
B
06
作业布置
【综合拓展类作业】
4.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克m元,售价每千克16元;乙种蔬菜进价每千克n元,售价每千克18元.
(1)该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元.求m,n的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克,求有哪几种购买方案.
06
作业布置
【综合拓展类作业】
(1)解:由题意得
,
解得: ;
答:m、n的值分别为10和14.
06
作业布置
【综合拓展类作业】
(2)解:根据题意 ,
解得: ,
因为x是整数
所以x为58、59、60 ;
∴共3种方案,分别为:
方案一购甲种蔬菜58千克,乙种蔬菜42千克;
方案二购甲种蔬菜59千克,乙种蔬菜41千克;
方案三购甲种蔬菜60千克,乙种蔬菜40千克.
07
板书设计
不等式的基本性质:
解一元一次不等式:
解一元一次不等式组:
第7章 小结与复习
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第7章 一元一次不等式与不等式组
小结与复习
01
教学目标
02
知识体系
03
回顾与思考
04
自评与互评
05
课堂练习
06
作业布置
01
教学目标
复习巩固不等式的概念及不等式的基本性质。
01
复习巩固一元一次不等式及其不等式组的解法,能够准确求解并正确表示解集。
02
能够正确分析实际问题中的不等关系,建立相应的不等式模型,能够准确列出不等式并求解。
03
02
知识体系
一元一次不等式与不等式组
不等式
一元一次不等式组
一元一次不等式
不等式的基本性质
03
回顾与思考
1.不等式的基本性质:
(1)_______________________________________________;
(2)_______________________________________________;
(3)_______________________________________________;
(4)_______________________________________________;
(5)_______________________________________________.
如果,那么,.
如果,,那么,.
如果,,那么,.
如果,那么.
如果,,那么.
03
回顾与思考
2.解一元一次不等式,就是根据不等式的基本性质和运算律,通过________________、______________、_________________、 ___________________、___________________等步骤,将原不等式变形为不等式ax>b(a≠0)的形式,再在不等式两边同除以未知数的系数a,从而得到不等式的解集x_____________________(当a>0时)[或x__________________(当a<0时)].
去分母
去括号
移项
合并同类项
x系数化为1
>
<
03
回顾与思考
3.解不等式组是求不等式组_________________的过程。
假设a>b,
(1)不等式组的解集为_______________;
(2)不等式组的解集为_______________;
(3)不等式组的解集为_______________;
(4)不等式组的解集为_______________。
解集
无解
03
回顾与思考
4.不等式(组)是反映现实世界数量之间不等关系的一个数学模型,建立不等式(组)模型解决实际问题的关键是:
(1)分析问题中有哪些数量;
(2)分析这些数量间的关系;
(3)建立不等式(组)模型.
04
自评与互评
1.解一元一次不等式(组)过程中,有哪些需要注意的问题 与同学们分享.
去分母:需要两边同时乘以分母的最小公倍数。但此时要注意,如果乘以的数是负数,不等号的方向需要改变。
去括号:在去除括号时,要特别注意括号前的符号。如果括号前是负号,那么括号内的每一项都要变号。移项:移项要变号。
系数化为1:如果除以的数是负数,不等号的方向需要改变。
04
自评与互评
1.解一元一次不等式(组)过程中,有哪些需要注意的问题 与同学们分享.
解集:不等式组的解集是满足所有不等式的x的集合。因此,需要找出所有不等式的交集。
在实际问题中:不等式的解往往需要符合实际情况,因此需要对解进行检验,确保其满足问题的实际背景。
04
自评与互评
2.方程和不等式都是描述现实生活中数量关系的重要模型,你能说说两者的相同点与不同点吗
相同点
1.基础概念:方程和不等式都基于数学中的等式和不等式关系,用于表示变量之间的数量关系。
2.未知数:在方程和不等式中,都包含未知数(通常用字母表示),这些未知数需要通过求解过程来确定。
3.求解方法:方程和不等式的求解都涉及一系列的数学运算和推理过程,如移项、合并同类项、求解等。
04
自评与互评
2.方程和不等式都是描述现实生活中数量关系的重要模型,你能说说两者的相同点与不同点吗
不同点
1.定义:方程是一个等式,表示两个数学表达式相等;而不等式则是一个关系式,表示两个数学表达式之间的大小关系(大于、小于、大于等于、小于等于)。
2.解的个数:对于方程,通常有一个或多个解(在某些情况下可能无解),这些解满足等式关系;而对于不等式,解通常是一个解集,表示满足不等式关系的所有可能值。
04
自评与互评
2.方程和不等式都是描述现实生活中数量关系的重要模型,你能说说两者的相同点与不同点吗
不同点
3.求解过程:
在求解方程时,目标是找到使等式成立的未知数的值;而在求解不等式时,目标是找到满足不等式关系的未知数的取值范围。
05
课堂练习
【知识技能类作业】必做题:
1.下列说法中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.若关于的不等式组有且只有三个整数解,则的最大值是( )
A.3 B.4 C.5 D.6
C
C
05
课堂练习
【知识技能类作业】必做题:
3.解不等式的过程如下:①去分母,得;②去括号,得;③移项,合并同类项,得;④系数化为1,得.其中错误的一步是( )
A.① B.② C.③ D.④
D
05
课堂练习
【知识技能类作业】选做题:
4.若不等式x>y和(a-3)x<(a-3)y成立,则a的取值范围是 .
5.若是关于的一元一次不等式,则的值为 .
6.若关于的不等式组无解,则的取值范围是 .
2
05
课堂练习
7.已知,;,;都是关于x,y的二元一次方程的解.
(1)求a,b的值;
(2)当x为何值时,y的值小于0.
(1)解:∵,;,;都是关于x,y的二元一次方程的解,
故将,;,代入二元一次方程得: ,
解得: .
【综合拓展类作业】
05
课堂练习
(2)解:由(1)可知,
所以,
若要是y的值小于0,即 ,
解得:,
∴当时,y的值小于0.
【综合拓展类作业】
06
作业布置
【知识技能类作业】
1.现有下列各式:①-3<0;②x+3y≥0;③x=3;④x2+xy+y2.其中不等式有( )
A.1个 B.2个 C.3个 D.4个
2.关于的不等式组的最小整数解为1,则的取值范围是( )
A. B.
C. D.或
3.已知不等式的正整数解恰好是1、2、3,则的取值范围是______________.
B
B
06
作业布置
【综合拓展类作业】
4.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克m元,售价每千克16元;乙种蔬菜进价每千克n元,售价每千克18元.
(1)该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元.求m,n的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克,求有哪几种购买方案.
06
作业布置
【综合拓展类作业】
(1)解:由题意得
,
解得: ;
答:m、n的值分别为10和14.
06
作业布置
【综合拓展类作业】
(2)解:根据题意 ,
解得: ,
因为x是整数
所以x为58、59、60 ;
∴共3种方案,分别为:
方案一购甲种蔬菜58千克,乙种蔬菜42千克;
方案二购甲种蔬菜59千克,乙种蔬菜41千克;
方案三购甲种蔬菜60千克,乙种蔬菜40千克.
07
板书设计
不等式的基本性质:
解一元一次不等式:
解一元一次不等式组:
第7章 小结与复习
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
