第五单元鸽巢问题课件(共13张PPT)人教版六年级下册数学
文档属性
| 名称 | 第五单元鸽巢问题课件(共13张PPT)人教版六年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 48.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 18:59:53 | ||
图片预览





文档简介
(共13张PPT)
鸽巢问题
总有
至少
情景导入
鸽巢问题是组合数学中一个重要的原理。在数学中有重要的作用,运用抽屉原理可以论证许多关于“存在”“总有”“至少有”的存在性问题
把4个苹果放进3个抽屉中,不论怎么放,一定会有什么现象存在呢?
探究新知
活动要求:
1、独立在平板上操作,摆一摆、填一填。
2、小组汇总小组内同学的摆法,并用“把4个苹果任意放进3个抽屉,不论怎么放,总有
的存在性。”这样的语句说一说你们得到的结论并记录在学习单上?
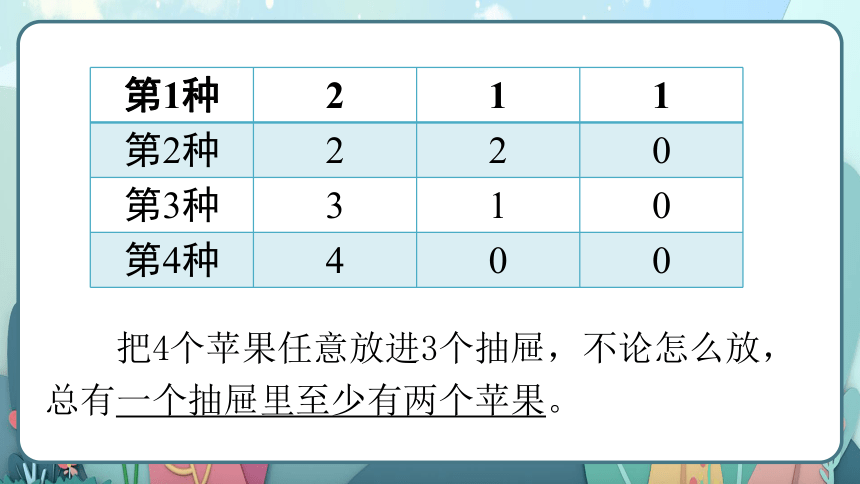
第1种 2 1 1
第2种 2 2 0
第3种 3 1 0
第4种 4 0 0
把4个苹果任意放进3个抽屉,不论怎么放,总有一个抽屉里至少有两个苹果。
一副扑克牌去掉大小王,还剩 52 张,请 5 位学生抽牌
如果有n+1个苹果放入n个抽屉,你能得出什么结论?
如果有n+1个苹果放入n个抽屉,一定有一个抽屉里至少有2个苹果。
如果有mn+1个苹果放入n个抽屉,你能得出什么结论?
如果有mn+1个苹果放入n个抽屉,一定有一个抽屉里至少有mn+1个苹果。
3、一天晚上,小红正要从自已放袜子的抽屉里取袜子,突然灯熄了。她知道自己的抽屉里放有白色、黄色2种颜色的袜子各6只。小红至少要摸出( )只袜子,才能保证拿出一双相同颜色的袜子。
2、把红、黄、蓝3种颜色的球各10个放到1个袋子里。至少取( )个球,可以保证取到两个颜色相同的球?
1、在一副扑克牌(去掉大王和小王)中抽牌,要想抽出的牌中一定有2张同种花色的,至少抽( )张;要想抽出的牌中一定有2张同样点数的,至少抽( )张
4、一个布袋中有40块相同的木块,木块上的号码是1、2、3、4 的各有10块。一次至少取出( )块木块,才能保证其中至少有3块木块上的号码相同。
组合作要求。
1.小组合作讨论,选取两个素材进行构建抽屉和物品。
2.可以试着画一画,算一算,连一连。
3.最后选取其中问题一个进行分享汇报。
同学们,通过本节课的学习,你有哪些收获?说一说解决“鸽巢问题”要注意什么?
课堂小结
谢谢观看
鸽巢问题
总有
至少
情景导入
鸽巢问题是组合数学中一个重要的原理。在数学中有重要的作用,运用抽屉原理可以论证许多关于“存在”“总有”“至少有”的存在性问题
把4个苹果放进3个抽屉中,不论怎么放,一定会有什么现象存在呢?
探究新知
活动要求:
1、独立在平板上操作,摆一摆、填一填。
2、小组汇总小组内同学的摆法,并用“把4个苹果任意放进3个抽屉,不论怎么放,总有
的存在性。”这样的语句说一说你们得到的结论并记录在学习单上?
第1种 2 1 1
第2种 2 2 0
第3种 3 1 0
第4种 4 0 0
把4个苹果任意放进3个抽屉,不论怎么放,总有一个抽屉里至少有两个苹果。
一副扑克牌去掉大小王,还剩 52 张,请 5 位学生抽牌
如果有n+1个苹果放入n个抽屉,你能得出什么结论?
如果有n+1个苹果放入n个抽屉,一定有一个抽屉里至少有2个苹果。
如果有mn+1个苹果放入n个抽屉,你能得出什么结论?
如果有mn+1个苹果放入n个抽屉,一定有一个抽屉里至少有mn+1个苹果。
3、一天晚上,小红正要从自已放袜子的抽屉里取袜子,突然灯熄了。她知道自己的抽屉里放有白色、黄色2种颜色的袜子各6只。小红至少要摸出( )只袜子,才能保证拿出一双相同颜色的袜子。
2、把红、黄、蓝3种颜色的球各10个放到1个袋子里。至少取( )个球,可以保证取到两个颜色相同的球?
1、在一副扑克牌(去掉大王和小王)中抽牌,要想抽出的牌中一定有2张同种花色的,至少抽( )张;要想抽出的牌中一定有2张同样点数的,至少抽( )张
4、一个布袋中有40块相同的木块,木块上的号码是1、2、3、4 的各有10块。一次至少取出( )块木块,才能保证其中至少有3块木块上的号码相同。
组合作要求。
1.小组合作讨论,选取两个素材进行构建抽屉和物品。
2.可以试着画一画,算一算,连一连。
3.最后选取其中问题一个进行分享汇报。
同学们,通过本节课的学习,你有哪些收获?说一说解决“鸽巢问题”要注意什么?
课堂小结
谢谢观看
