8.1.1 课时2 三角形的中线、角平分线和高 (共16张PPT) 2024-2025学年华东师大版(2024)数学七年级下册
文档属性
| 名称 | 8.1.1 课时2 三角形的中线、角平分线和高 (共16张PPT) 2024-2025学年华东师大版(2024)数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 20:46:17 | ||
图片预览





文档简介
(共16张PPT)
8.1.1.认识三角形
课时2 三角形的中线、角平分线和高
1.掌握三角形的高,中线及角平分线的概念
2.会画三角形的高,中线及角平分线.
3.会画钝角三角形的两短边上的高.
回顾:前面我们学了三角形的概念,三角形有哪些组成元素?
三条边、三个角、三个顶点
三角形除了三边,还有哪些线段呢?
三角形的中线
问题1 如图,如果点C是线段AB的中点,你能得到什么结论?
A
C
B
AC=BC=AB
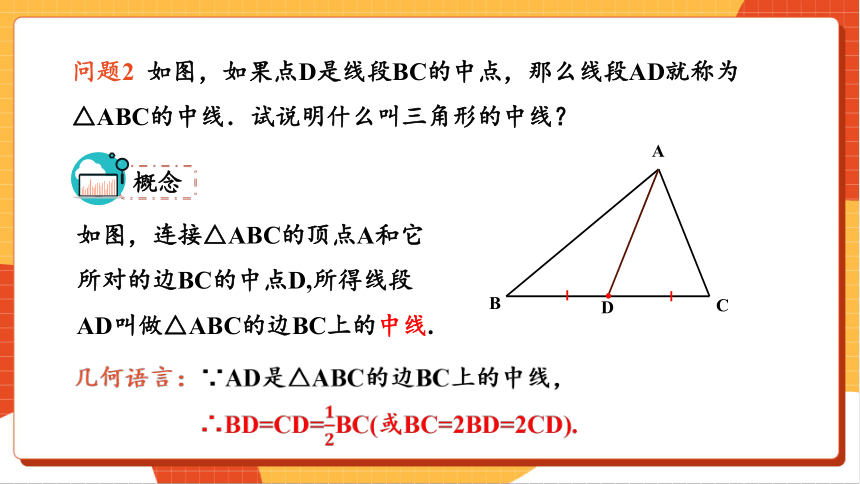
问题2 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.试说明什么叫三角形的中线?
A
B
C
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
几何语言:∵AD是△ABC的边BC上的中线,
∴BD=CD=BC(或BC=2BD=2CD).
D
概念
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
规律:三角形的三条中线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
画一画
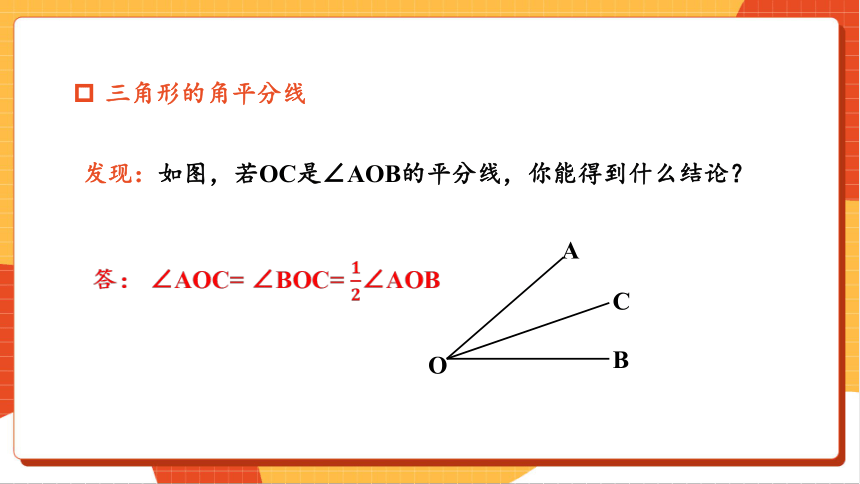
发现:如图,若OC是∠AOB的平分线,你能得到什么结论?
A
C
B
O
答: ∠AOC= ∠BOC= ∠AOB
三角形的角平分线
如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.
B
C
D
A
(
(
几何语言:
∵AD是△ABC的角平分线,
∴∠BAD= ∠CAD= ∠BAC
(或∠BAC=2∠BAD=2∠CAD).
答:相同点是:∠BAD= ∠CAD;
不同点是:前者是线段,后者是射线.
发现:三角形的角平分线与角的角平分线有何相同点和不同点?
概念
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,并观察它们的交点有什么规律?
规律:三角形的三条角平分线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
画一画
三角形的高
问题1 什么是三角形的高?
问题2 怎样画三角形的高?
如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
A
B
C
D
垂直符号
垂足
几何语言:∵AD是△ABC的边BC上的高,
∴AD⊥BC(或∠ADB= ∠ADC=90°).
概念
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
规律:三角形的三条高所在的直线交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
O
(E,F)
O
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条高,并观察高的交点有什么规律?
画一画
由前面的操作,我们可以发现,
三角形的三条中线、三条角平分线和三条高(或所在的直线)分别____________;
直角三角形三条高的交点就是____________;
钝角三角形有两条高位于三角形的外部.
交于一点
直角顶点
归纳
例1 如图,在△ABC中,请作图:
(1)画出△ABC的∠C的平分线;
(2)画出△ABC的边AC上的中线;
(3)画出△ABC的边BC上的高.
A
B
C
D
E
F
答:如图,CF是∠ACB的角平分线;BE是AC边上的中线;AD是边BC上的高.
注意 :画高要标明垂直符号.三角形的角平分线,
中线及高都要画成线段.
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
1.下列各组图形中,哪一组图形中AD是△ABC的BC边上的高( )
2.如图是一张三角形纸片,请你动手画出它的BC边上的中线,BC边上的高,∠A的平分线.
A
B
C
D
AD为中线(BD=DC)
E
AE为高(AE⊥BC)
)
)
AF 为∠A的平分线(∠BAF=∠CAF)
F
答:如图,AD为所求中线,AE为所求高,AF为所求角平分线.
中线
三角形的重要线段
角平分线
高
注意:钝角三角形两短边的
高的画法
8.1.1.认识三角形
课时2 三角形的中线、角平分线和高
1.掌握三角形的高,中线及角平分线的概念
2.会画三角形的高,中线及角平分线.
3.会画钝角三角形的两短边上的高.
回顾:前面我们学了三角形的概念,三角形有哪些组成元素?
三条边、三个角、三个顶点
三角形除了三边,还有哪些线段呢?
三角形的中线
问题1 如图,如果点C是线段AB的中点,你能得到什么结论?
A
C
B
AC=BC=AB
问题2 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.试说明什么叫三角形的中线?
A
B
C
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
几何语言:∵AD是△ABC的边BC上的中线,
∴BD=CD=BC(或BC=2BD=2CD).
D
概念
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
规律:三角形的三条中线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
画一画
发现:如图,若OC是∠AOB的平分线,你能得到什么结论?
A
C
B
O
答: ∠AOC= ∠BOC= ∠AOB
三角形的角平分线
如图,在△ABC中,如果∠BAC的平分线AD交BC边于点D,我们就称AD是△ABC的角平分线.
B
C
D
A
(
(
几何语言:
∵AD是△ABC的角平分线,
∴∠BAD= ∠CAD= ∠BAC
(或∠BAC=2∠BAD=2∠CAD).
答:相同点是:∠BAD= ∠CAD;
不同点是:前者是线段,后者是射线.
发现:三角形的角平分线与角的角平分线有何相同点和不同点?
概念
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,并观察它们的交点有什么规律?
规律:三角形的三条角平分线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
画一画
三角形的高
问题1 什么是三角形的高?
问题2 怎样画三角形的高?
如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
A
B
C
D
垂直符号
垂足
几何语言:∵AD是△ABC的边BC上的高,
∴AD⊥BC(或∠ADB= ∠ADC=90°).
概念
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
规律:三角形的三条高所在的直线交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
O
(E,F)
O
如图,分别画出锐角三角形、直角三角形、钝角三角形的三条高,并观察高的交点有什么规律?
画一画
由前面的操作,我们可以发现,
三角形的三条中线、三条角平分线和三条高(或所在的直线)分别____________;
直角三角形三条高的交点就是____________;
钝角三角形有两条高位于三角形的外部.
交于一点
直角顶点
归纳
例1 如图,在△ABC中,请作图:
(1)画出△ABC的∠C的平分线;
(2)画出△ABC的边AC上的中线;
(3)画出△ABC的边BC上的高.
A
B
C
D
E
F
答:如图,CF是∠ACB的角平分线;BE是AC边上的中线;AD是边BC上的高.
注意 :画高要标明垂直符号.三角形的角平分线,
中线及高都要画成线段.
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
1.下列各组图形中,哪一组图形中AD是△ABC的BC边上的高( )
2.如图是一张三角形纸片,请你动手画出它的BC边上的中线,BC边上的高,∠A的平分线.
A
B
C
D
AD为中线(BD=DC)
E
AE为高(AE⊥BC)
)
)
AF 为∠A的平分线(∠BAF=∠CAF)
F
答:如图,AD为所求中线,AE为所求高,AF为所求角平分线.
中线
三角形的重要线段
角平分线
高
注意:钝角三角形两短边的
高的画法
