1.1.5 多项式的乘法——单项式乘多项式 课件(共22张PPT)
文档属性
| 名称 | 1.1.5 多项式的乘法——单项式乘多项式 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 08:44:07 | ||
图片预览








文档简介
(共22张PPT)
单项式乘多项式
七年级下册 第一章 1.1.5
学习目标
1.理解单项式乘多项式的运算法则,能用数学语言表述“单项式分别乘以多项式的每一项,再将所得的积相加”。
2.能熟练运用法则进行单项式乘多项式的计算。
3.会利用单项式乘多项式解决简单的实际问题。
问题导入
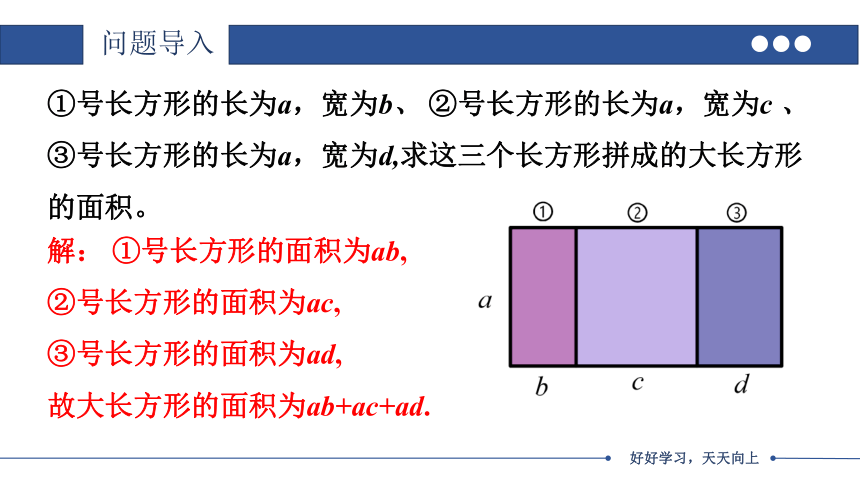
①号长方形的长为a,宽为b、 ②号长方形的长为a,宽为c 、 ③号长方形的长为a,宽为d,求这三个长方形拼成的大长方形的面积。
解: ①号长方形的面积为ab,
②号长方形的面积为ac,
③号长方形的面积为ad,
故大长方形的面积为ab+ac+ad.
问题导入
①号长方形的长为a,宽为b、 ②号长方形的长为a,宽为c 、 ③号长方形的长为a,宽为d,求这三个长方形拼成的大长方形的面积。
解: 大长方形的宽为a,
大长方形的长为b+c+d,
故大长方形的面积为
a(b+c+d)=ab+ac+ad.
问题导入
乘法对加法的分配律:
(a+b)×c=a×c+b×c
a×(b+c)=a×b+a×c
回顾
规定:单项式与多项式相乘的法则的目标是使整式的乘法满足乘法对加法的分配律.
新知探究
思考
怎样计算单项式2x与多项式3x2-x-5的乘积?
要将3x2-x-5看作各项的代数和。
解:2x·(3x2-x-5)
=2x·3x2+2x·(-x)+2x ·(-5)
=6x3-2x2-10x
新知探究
归纳
法则:
单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.
m·(a+b+…+p)=ma+mb+…+mp (m,a,b,…,p都是单项式)
(a+b+…+p)·m=am+bm+…+pm (m,a,b,…,p都是单项式)
新知探究
一般步骤:
1.利用分配律,转化为单项式乘单项式
2.将单项式与单项式相乘的结果相加
例题探究
例11 计算:(1) 2x2 ;
(2) (15xy) .
解:(1) 原式=2x2
=8x3y-x3+2x2.
(2) 原式=(-3x2) (-15xy)+ (-15xy)
=45x3y-3xy3.
例题探究
议一议
下列计算对不对 如果不对,应怎样改正
(1) (3x2y-xy2) x=3x2y-xy2;
(2) (-2x) (x2+3x-1)=-2x3-6x2-2;
(3) =.
例题探究
解:(1)错误, (3x2y-xy2) x
(2)错误,(-2x) (x2+3x-1)
=3x2y x+(-xy2) x
=3x3y-x2y2;
= (-2x) x2+(-2x) 3x+(-2x) (-1)
=-2x3-6x2+2x
(3)正确.
例12 (1) 计算: (4xy-6y2)-4x2(-xy)
(2) 当 x 取 2,y 取 -1 时,求 (1) 中多项式的值.
例题探究
解:(1)原式= 4xy+(-6y2)+4x3y
=-2x3y+3x2y2+4x3y
=2x3y+3x2y2.
(2) 将x用2代入,y用-1代入,(1)中多项式的值为
2×23×(-1)+3×22×(-1)2=-16+12=-4.
1.计算-2x·(5x+2)的结果是( )
A.-10x2-2
B. 10x2+4x
C. 10x2-4x
D. -10x2-4x
课堂练习
D
2.计算:a(a+2)-2a= ( )
A.2
B.a2
C.a2+2a
D.a2-2a
课堂练习
B
3.一个长方体的长、宽、高分别为3a-4,2a,a,它的体积等于 ( )
A.3a3-4a2
B. a2
C. 6a3-8a2
D. 6a3-8a
课堂练习
C
4.如果计算(-4x2)·(2-nx+3x2+mx3)的结果中不含x5项,那么m的值为 ( )
A.0
B.1
C.-1
D.-
课堂练习
A
5.计算:
(1)(-2a2b)3·(3b2-4a+6). (2)-2x3[x3-x2(4x+1)].
课堂练习
解: (1)原式=-8a6b3·(3b2-4a+6)=-24a6b5+32a7b3-48a6b3.
(2)原式=-2x3(x3-4x3-x2)=-2x3(-3x3-x2)=6x6+2x5.
6.某同学计算一个多项式乘-3x2时,因抄错符号,写成了加上-3x2,得到的答案是x2-2x+1.
(1)求这个多项式.
(2)正确的计算结果应该是多少
课堂探究
解: (1)多项式是x2-2x+1-(-3x2)=x2-2x+1+3x2=4x2-2x+1.
(2)(4x2-2x+1)·(-3x2)=-12x4+6x3-3x2,
即正确的计算结果为-12x4+6x3-3x2.
7.先化简,再求值:x(x2-6x-9)-x(x2-8x-15)+2x(3-x),其中x=.
课堂探究
解:x(x2-6x-9)-x(x2-8x-15)+2x(3-x)
=x3-6x2-9x-x3+8x2+15x+6x-2x2
=12x.
当x=时,原式的值为12×()=-2
课堂小结
法则:
单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.
m·(a+b+…+p)=ma+mb+…+mp (m,a,b,…,p都是单项式)
(a+b+…+p)·m=am+bm+…+pm (m,a,b,…,p都是单项式)
一般步骤:
1.利用分配律,转化为单项式乘单项式
2.将单项式与单项式相乘的结果相加
课后作业
课堂作业:P14 T6
单项式乘多项式
七年级下册 第一章 1.1.5
学习目标
1.理解单项式乘多项式的运算法则,能用数学语言表述“单项式分别乘以多项式的每一项,再将所得的积相加”。
2.能熟练运用法则进行单项式乘多项式的计算。
3.会利用单项式乘多项式解决简单的实际问题。
问题导入
①号长方形的长为a,宽为b、 ②号长方形的长为a,宽为c 、 ③号长方形的长为a,宽为d,求这三个长方形拼成的大长方形的面积。
解: ①号长方形的面积为ab,
②号长方形的面积为ac,
③号长方形的面积为ad,
故大长方形的面积为ab+ac+ad.
问题导入
①号长方形的长为a,宽为b、 ②号长方形的长为a,宽为c 、 ③号长方形的长为a,宽为d,求这三个长方形拼成的大长方形的面积。
解: 大长方形的宽为a,
大长方形的长为b+c+d,
故大长方形的面积为
a(b+c+d)=ab+ac+ad.
问题导入
乘法对加法的分配律:
(a+b)×c=a×c+b×c
a×(b+c)=a×b+a×c
回顾
规定:单项式与多项式相乘的法则的目标是使整式的乘法满足乘法对加法的分配律.
新知探究
思考
怎样计算单项式2x与多项式3x2-x-5的乘积?
要将3x2-x-5看作各项的代数和。
解:2x·(3x2-x-5)
=2x·3x2+2x·(-x)+2x ·(-5)
=6x3-2x2-10x
新知探究
归纳
法则:
单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.
m·(a+b+…+p)=ma+mb+…+mp (m,a,b,…,p都是单项式)
(a+b+…+p)·m=am+bm+…+pm (m,a,b,…,p都是单项式)
新知探究
一般步骤:
1.利用分配律,转化为单项式乘单项式
2.将单项式与单项式相乘的结果相加
例题探究
例11 计算:(1) 2x2 ;
(2) (15xy) .
解:(1) 原式=2x2
=8x3y-x3+2x2.
(2) 原式=(-3x2) (-15xy)+ (-15xy)
=45x3y-3xy3.
例题探究
议一议
下列计算对不对 如果不对,应怎样改正
(1) (3x2y-xy2) x=3x2y-xy2;
(2) (-2x) (x2+3x-1)=-2x3-6x2-2;
(3) =.
例题探究
解:(1)错误, (3x2y-xy2) x
(2)错误,(-2x) (x2+3x-1)
=3x2y x+(-xy2) x
=3x3y-x2y2;
= (-2x) x2+(-2x) 3x+(-2x) (-1)
=-2x3-6x2+2x
(3)正确.
例12 (1) 计算: (4xy-6y2)-4x2(-xy)
(2) 当 x 取 2,y 取 -1 时,求 (1) 中多项式的值.
例题探究
解:(1)原式= 4xy+(-6y2)+4x3y
=-2x3y+3x2y2+4x3y
=2x3y+3x2y2.
(2) 将x用2代入,y用-1代入,(1)中多项式的值为
2×23×(-1)+3×22×(-1)2=-16+12=-4.
1.计算-2x·(5x+2)的结果是( )
A.-10x2-2
B. 10x2+4x
C. 10x2-4x
D. -10x2-4x
课堂练习
D
2.计算:a(a+2)-2a= ( )
A.2
B.a2
C.a2+2a
D.a2-2a
课堂练习
B
3.一个长方体的长、宽、高分别为3a-4,2a,a,它的体积等于 ( )
A.3a3-4a2
B. a2
C. 6a3-8a2
D. 6a3-8a
课堂练习
C
4.如果计算(-4x2)·(2-nx+3x2+mx3)的结果中不含x5项,那么m的值为 ( )
A.0
B.1
C.-1
D.-
课堂练习
A
5.计算:
(1)(-2a2b)3·(3b2-4a+6). (2)-2x3[x3-x2(4x+1)].
课堂练习
解: (1)原式=-8a6b3·(3b2-4a+6)=-24a6b5+32a7b3-48a6b3.
(2)原式=-2x3(x3-4x3-x2)=-2x3(-3x3-x2)=6x6+2x5.
6.某同学计算一个多项式乘-3x2时,因抄错符号,写成了加上-3x2,得到的答案是x2-2x+1.
(1)求这个多项式.
(2)正确的计算结果应该是多少
课堂探究
解: (1)多项式是x2-2x+1-(-3x2)=x2-2x+1+3x2=4x2-2x+1.
(2)(4x2-2x+1)·(-3x2)=-12x4+6x3-3x2,
即正确的计算结果为-12x4+6x3-3x2.
7.先化简,再求值:x(x2-6x-9)-x(x2-8x-15)+2x(3-x),其中x=.
课堂探究
解:x(x2-6x-9)-x(x2-8x-15)+2x(3-x)
=x3-6x2-9x-x3+8x2+15x+6x-2x2
=12x.
当x=时,原式的值为12×()=-2
课堂小结
法则:
单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.
m·(a+b+…+p)=ma+mb+…+mp (m,a,b,…,p都是单项式)
(a+b+…+p)·m=am+bm+…+pm (m,a,b,…,p都是单项式)
一般步骤:
1.利用分配律,转化为单项式乘单项式
2.将单项式与单项式相乘的结果相加
课后作业
课堂作业:P14 T6
同课章节目录
