沪教版九年级数学上册 24.4 平面向量的线性运算 练习(含详解)
文档属性
| 名称 | 沪教版九年级数学上册 24.4 平面向量的线性运算 练习(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 08:34:50 | ||
图片预览



文档简介
第二十四章第四节 平面向量的线性运算
一、单选题
1.已知、为非零向量,下列判断错误的是( )
A.如果,那么 B.如果,那么
C.如果,那么或 D.如果为单位向量,且,那么
2.矩形的对角线与相交于点,如果,,那么( )
A. B.
C. D.
3.如图,在中,点D是在边上一点,且,,,那么等于( )
A. B. C. D.
4.下列命题正确的个数是( )
①设是一个实数,是向量,那么与相乘的积是一个向量;
②如果,,那么的模是;
③如果,或,那么;
④如果,的方向与的方向相反.
A.1个 B.2个 C.3个 D.4个
5.如图,平行四边形中,E是边的中点,联结,设,那么下列向量中,可表示为的是( )
A. B. C. D.
6.已知、是两个单位向量,向量,,那么下列结论正确的是( )
A. B. C. D.
7.下列说法不正确的是( )
A.设为单位向量,那么
B.已知、、都是非零向量,如果,,那么
C.四边形中,如果满足,,那么这个四边形一定是平行四边形
D.平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解
8.下列判断错误的是( )
A.0
B.如果+=2,-=3,其中,那么∥
C.设为单位向量,那么||=1
D.如果||=2||,那么=2或=-2
9.如图,在△ABC中,点D、E分别是边BC、AC的中点,AD和BE交于点G,设,,那么向量用向量、表示为( )
A. B. C. D.
10.已知单位向量与非零向量、,下列四个选项中,正确的是( )
A. B. C. D.
二、填空题
11.化简: .
12.已知向量和方向相反,长度为7,则用来表示为: (为单位向量).
13.如图,在 ABC中,点D是的中点,设,,那么可以用含、的式子表示为 .
14.如图,已知点M、N分别在 ABC的边、上,,且,设,用表示,则 .
15.已知点G是 ABC的重心,设,,那么用、可表示为 .
16.如图,在平行四边形中,点是边中点,点是边上的点,且设,,那么可用、表示为 .
17.已知,分别是,相同方向上的单位向量, .
18.如图,在中,点E和点F分别在和上,,将沿直线翻折,点D落在边上的点G处,若则= (用表示)
三、解答题
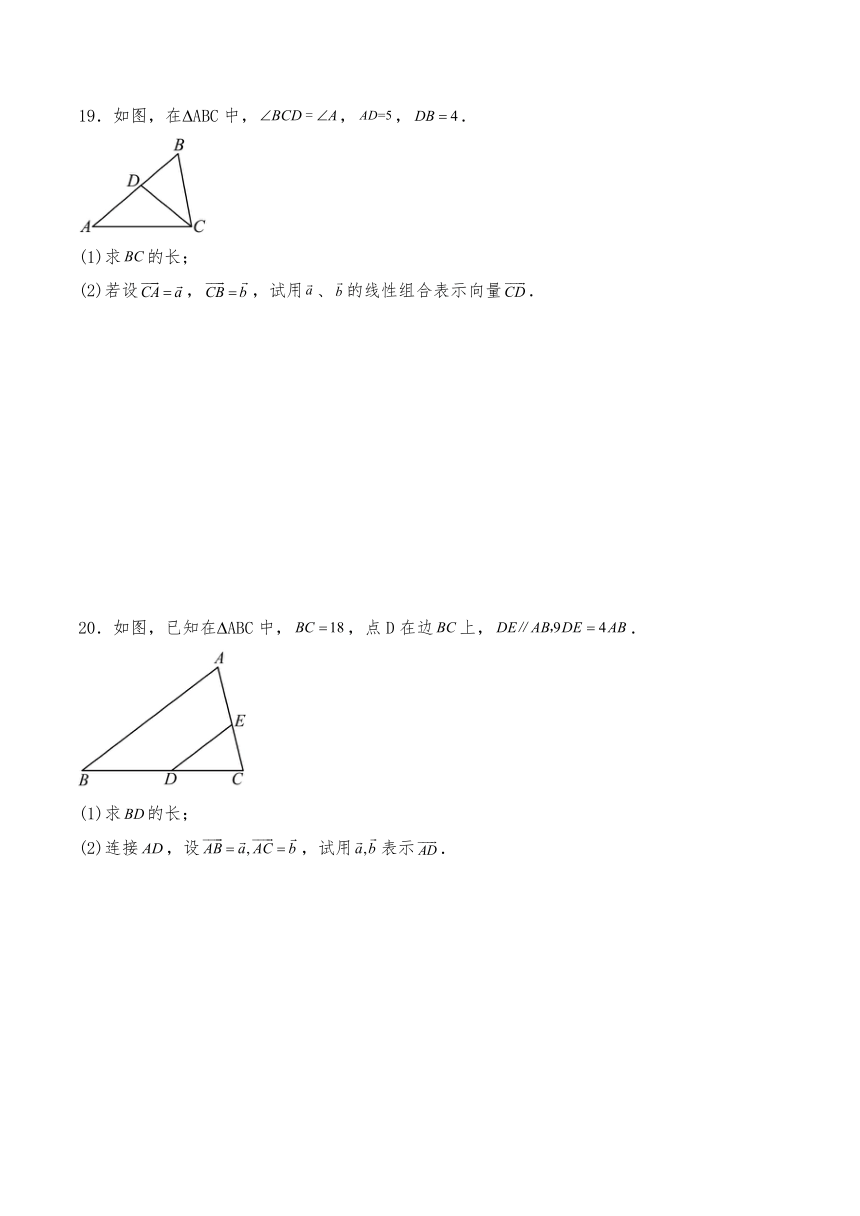
19.如图,在 ABC中,,,.
(1)求的长;
(2)若设,,试用、的线性组合表示向量.
20.如图,已知在 ABC中,,点D在边上,.
(1)求的长;
(2)连接,设,试用表示.
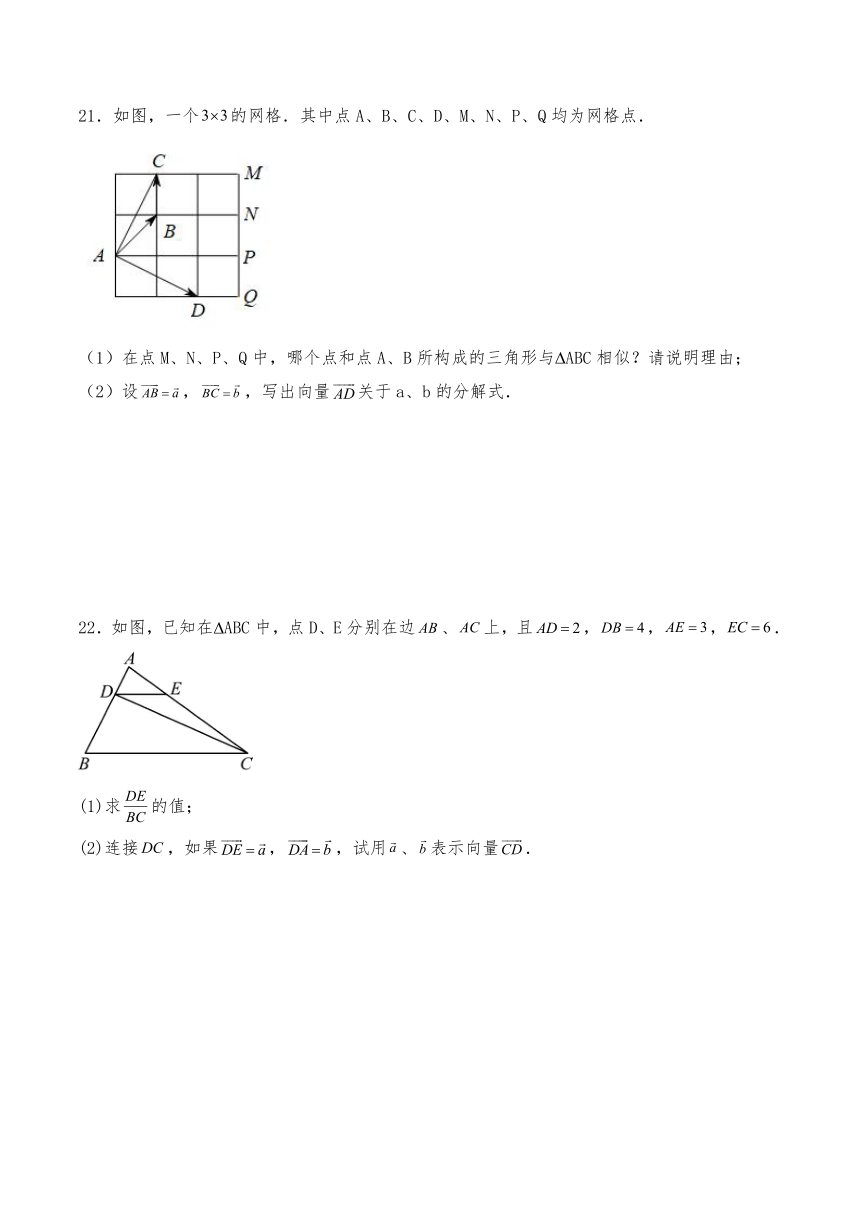
21.如图,一个的网格.其中点A、B、C、D、M、N、P、Q均为网格点.
(1)在点M、N、P、Q中,哪个点和点A、B所构成的三角形与 ABC相似?请说明理由;
(2)设,,写出向量关于a、b的分解式.
22.如图,已知在 ABC中,点D、E分别在边、上,且,,,.
(1)求的值;
(2)连接,如果,,试用、表示向量.
23.如图,在平行四边形中,点为上的一点,,与相交于点,如果,,
(1)用向量、分别表示下列向量; ; ;
(2)在图中求作分别在、方向上的分向量.(不要求写作法,但要保留作图痕迹,并写明结论)
24.如图,已知相交于点,过作交于点,.
(1)求的值;
(2)设,用向量表示.
25.如图,在中,是的重心,联结并延长交于点.
(1)如果,,那么=________________(用向量、表示);
(2)已知,,点在边上,且,求的长.
26.如图,在 ABC中,点是 ABC的重心,联结,联结并延长交边于点,过点作交边于点.
(1)如果,,用、表示向量;
(2)当,,时,求的长.
答案
一、单选题
1.C
【分析】根据单位向量、平行向量以及模的定义进行判断即可.
【解析】解:A、如果,那么,故本选正确;
B、如果,那么,故本选正确;
C、如果,没法判断与之间的关系,故本选项错误
D、如果为单位向量,且,那么,故本选正确;
故选:C.
2.B
【解析】解:如图所示:
∵
∴,
故选:B.
3.D
【分析】由,求得的值,然后结合平面向量的三角形法则求得的值.
【解析】解:∵,
∴.
∵,
∴.
又,
∴.
故选:D.
4.B
【分析】根据实数与向量的乘积结合向量的定义,逐项分析判断即可求解.
【解析】解:①设是一个实数,是向量,那么与相乘的积是一个向量,故①正确;
②如果,,那么的模是,故②正确;
③如果,或,那么,故③错误;
④如果,的方向与的方向相反,故④错误,
故选:B.
5.A
【分析】根据平行四边形的性质得到AD=BC;然后利用三角形法则解答即可.
【解析】解:在平行四边形中,,.
∵,
∴.
∵E是边的中点,,
∴.
∴.
故选:A.
6.C
7.C
【分析】根据单位向量的定义(模等于1的向量),向量平行的定义(指方向相同或相反的非零向量)以及平行四边形的判定进行判断.
【解析】解:A、设为单位向量,那么,故本选项说法正确.
B、已知、、都是非零向量,如果,,那么、方向相反,则,故本选项说法正确.
C、四边形中,如果满足,即,不能判定这个四边形一定是平行四边形,故本选项说法错误.
D、由平面向量的平行四边形法则可以推知,平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解,故本选项说法正确.
故选:C.
8.下D
【分析】根据平面向量的定义、向量的模以及平行向量的定义解答.
【解析】A、0 ,故本选项不符合题意.
B、由+=2,-=3得到:=,=﹣,故两向量方向相反,∥,故本选项不符合题意.
C、为单位向量,那么||=1,故本选项不符合题意.
D、由||=2||只能得到两向量模间的数量关系,不能判断其方向,判断错误,故本选项符合题意.
故选D.
9.A
【分析】利用三角形法则求出,再根据三角形中心的性质解决问题即可.
【解析】解:∵,,
∴,
∵AD,BE是△ABC的中线,
∴G是△ABC的重心,
∴BG=BE,
∴=,
故选A.
10.B
【分析】根据平面向量的定义,平面向量模的定义以及共线向量的定义进行判断即可.
【解析】A.当单位概率与非零向量的方向相同时才成立,故该选项不正确,不符合题意;
B. ,故该选项正确,符合题意;
C.当非零向量,的方向相同时才成立,故该选项不正确,不符合题意;
D. 当单位概率与非零向量的方向相同时才成立,故该选项不正确,不符合题意;
故选B
二、填空题
11.
【分析】本题考查向量的加减运算,根据向量加减运算法则求解即可
【解析】解:
,
故答案为:.
12.
【分析】本题考查了平面向量的线性表示法,熟练掌握平面向量的性质是解题的关键.根据平面向量与单位向量方向相反,长度为7,即可得出结论.
【解析】解:∵向量和方向相反,长度为7,
∴.
故答案为: .
13.
【分析】本题主要考查了平面向量,先求出,再利用三角形法则求得答案.
【解析】解:∵,点D是的中点,
∴,
又∵,
∴,
故答案为:.
14.
【分析】本题考查了相似三角形的判定和性质,向量的定义.先根据,得,再根据相似三角形的性质及向量的定义即可,本题的关键是熟练掌握相似三角形的判定和性质.
【解析】解:,
,
,
,
,
,
故答案为:.
15.
【分析】如图,先根据向量的减法法则求出,根据D点是边的中点求出,再由向量的加法法则求出,然后根据G是 ABC的重心即可求出.
【解析】如图,D点是边的中点,G是 ABC的重心,
∵,,
∴
∵D点是边的中点,
∴,
∴,
∵G是的重心,
∴.
故答案为:.
16.
【分析】本题考查的知识点是向量的线性运算、平行四边形的性质,解题关键是熟练掌握向量的线性运算.
首先由四边形是平行四边形,求得,又由点是边中点,点是边上的点,且,求得与,再利用三角形法则求解即可.
【解析】解:四边形是平行四边形,
,
点是边中点,点是边上的点,且,
,,
.
故答案为:.
17.
【分析】本题考查了向量的运算,根据向量的相关运算法则计算即可.
【解析】解:,
故答案为:.
18.
【分析】根据翻折的性质、相似三角形的性质、相似三角形是判定及比例的性质求解.本题考查了翻折变换,掌握翻折的性质、相似三角形的性质、相似三角形是判定及比例的性质是解题的关键.
【解析】解:连接交于,交于点,
将沿直线翻折,点落在边上的点处,
,,
,
,
,
,
,
在中,,
,
,
,
∴
故答案为:.
三、解答题
19.(1)∵,
,
∴,
∴,即,
∴或(不符合题意,舍去),
∴的长为6;
(2)∵,
∴,
∴=,
∴.
20.(1)解:∵,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴
21.解:(1)点N和点A、B所构成的三角形与 ABC相似,理由如下:
设网格中小正方形的边长为a,
则BC=a,AB=, AC=,其中BC<AB<AC
如下图所示,连接BM、AM
则BM=,AM=,其中AB<BM<AM
∴,
∴≠
∴和 ABC不相似;
如下图所示,连接AN
则BN=2a,AN=,其中AB<BN<AN
∴,,,
∴==
∴∽ ABC;
如下图所示,连接BP
则BP=,AP=3,其中AB<BP<AP
∴,
∴≠
∴和 ABC不相似;
如下图所示,连接BQ、AQ
则BQ=,AQ=,其中AB<BQ<AQ
∴,
∴≠
∴和 ABC不相似;
综上:点N和点A、B所构成的三角形与 ABC相似;
(2)延长AB至E,使BE=AB,根据正方形的性质可知,点E正好落在格点上,如下图所示
∴,
∴=+
=.
22.(1)解: ,,,,
,
,
,
.
(2)解:由(1)中可知,
,
,
∴.
23.(1)解:∵四边形是平行四边形
∴,,
∴,,
∵
∴
∵
∴;
∵
∴
∴
∴,
∵
∴;
(2)如图,即为分别在、方向上的分向量.
24.(1)解:∵,
∴,,
∴ ABE∽ DCE,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
(2)由(1)得,则,
∵,
∴,
由(1)得,
∴,
则.
25.(1)解:,,
是的重心,联结并延长交于点,
为的边上的中线,
即点为的中点,
,
故答案为:.
(2)是的重心,
.
,,
,
26.解:(1)∵,
∵点G是Rt△ABC的重心,
∴AD=AC,
∵,,
∴,
∴
∴,
.
(2)∵G是三角形的重心,
∴BG=2GD,AD=DC,
∵BG=6,
∴GD=3,
∵,,
∴AG=GD=3,
∴,
∵,
∴,
∴DE=,
∴AE=AD+DE=
一、单选题
1.已知、为非零向量,下列判断错误的是( )
A.如果,那么 B.如果,那么
C.如果,那么或 D.如果为单位向量,且,那么
2.矩形的对角线与相交于点,如果,,那么( )
A. B.
C. D.
3.如图,在中,点D是在边上一点,且,,,那么等于( )
A. B. C. D.
4.下列命题正确的个数是( )
①设是一个实数,是向量,那么与相乘的积是一个向量;
②如果,,那么的模是;
③如果,或,那么;
④如果,的方向与的方向相反.
A.1个 B.2个 C.3个 D.4个
5.如图,平行四边形中,E是边的中点,联结,设,那么下列向量中,可表示为的是( )
A. B. C. D.
6.已知、是两个单位向量,向量,,那么下列结论正确的是( )
A. B. C. D.
7.下列说法不正确的是( )
A.设为单位向量,那么
B.已知、、都是非零向量,如果,,那么
C.四边形中,如果满足,,那么这个四边形一定是平行四边形
D.平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解
8.下列判断错误的是( )
A.0
B.如果+=2,-=3,其中,那么∥
C.设为单位向量,那么||=1
D.如果||=2||,那么=2或=-2
9.如图,在△ABC中,点D、E分别是边BC、AC的中点,AD和BE交于点G,设,,那么向量用向量、表示为( )
A. B. C. D.
10.已知单位向量与非零向量、,下列四个选项中,正确的是( )
A. B. C. D.
二、填空题
11.化简: .
12.已知向量和方向相反,长度为7,则用来表示为: (为单位向量).
13.如图,在 ABC中,点D是的中点,设,,那么可以用含、的式子表示为 .
14.如图,已知点M、N分别在 ABC的边、上,,且,设,用表示,则 .
15.已知点G是 ABC的重心,设,,那么用、可表示为 .
16.如图,在平行四边形中,点是边中点,点是边上的点,且设,,那么可用、表示为 .
17.已知,分别是,相同方向上的单位向量, .
18.如图,在中,点E和点F分别在和上,,将沿直线翻折,点D落在边上的点G处,若则= (用表示)
三、解答题
19.如图,在 ABC中,,,.
(1)求的长;
(2)若设,,试用、的线性组合表示向量.
20.如图,已知在 ABC中,,点D在边上,.
(1)求的长;
(2)连接,设,试用表示.
21.如图,一个的网格.其中点A、B、C、D、M、N、P、Q均为网格点.
(1)在点M、N、P、Q中,哪个点和点A、B所构成的三角形与 ABC相似?请说明理由;
(2)设,,写出向量关于a、b的分解式.
22.如图,已知在 ABC中,点D、E分别在边、上,且,,,.
(1)求的值;
(2)连接,如果,,试用、表示向量.
23.如图,在平行四边形中,点为上的一点,,与相交于点,如果,,
(1)用向量、分别表示下列向量; ; ;
(2)在图中求作分别在、方向上的分向量.(不要求写作法,但要保留作图痕迹,并写明结论)
24.如图,已知相交于点,过作交于点,.
(1)求的值;
(2)设,用向量表示.
25.如图,在中,是的重心,联结并延长交于点.
(1)如果,,那么=________________(用向量、表示);
(2)已知,,点在边上,且,求的长.
26.如图,在 ABC中,点是 ABC的重心,联结,联结并延长交边于点,过点作交边于点.
(1)如果,,用、表示向量;
(2)当,,时,求的长.
答案
一、单选题
1.C
【分析】根据单位向量、平行向量以及模的定义进行判断即可.
【解析】解:A、如果,那么,故本选正确;
B、如果,那么,故本选正确;
C、如果,没法判断与之间的关系,故本选项错误
D、如果为单位向量,且,那么,故本选正确;
故选:C.
2.B
【解析】解:如图所示:
∵
∴,
故选:B.
3.D
【分析】由,求得的值,然后结合平面向量的三角形法则求得的值.
【解析】解:∵,
∴.
∵,
∴.
又,
∴.
故选:D.
4.B
【分析】根据实数与向量的乘积结合向量的定义,逐项分析判断即可求解.
【解析】解:①设是一个实数,是向量,那么与相乘的积是一个向量,故①正确;
②如果,,那么的模是,故②正确;
③如果,或,那么,故③错误;
④如果,的方向与的方向相反,故④错误,
故选:B.
5.A
【分析】根据平行四边形的性质得到AD=BC;然后利用三角形法则解答即可.
【解析】解:在平行四边形中,,.
∵,
∴.
∵E是边的中点,,
∴.
∴.
故选:A.
6.C
7.C
【分析】根据单位向量的定义(模等于1的向量),向量平行的定义(指方向相同或相反的非零向量)以及平行四边形的判定进行判断.
【解析】解:A、设为单位向量,那么,故本选项说法正确.
B、已知、、都是非零向量,如果,,那么、方向相反,则,故本选项说法正确.
C、四边形中,如果满足,即,不能判定这个四边形一定是平行四边形,故本选项说法错误.
D、由平面向量的平行四边形法则可以推知,平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解,故本选项说法正确.
故选:C.
8.下D
【分析】根据平面向量的定义、向量的模以及平行向量的定义解答.
【解析】A、0 ,故本选项不符合题意.
B、由+=2,-=3得到:=,=﹣,故两向量方向相反,∥,故本选项不符合题意.
C、为单位向量,那么||=1,故本选项不符合题意.
D、由||=2||只能得到两向量模间的数量关系,不能判断其方向,判断错误,故本选项符合题意.
故选D.
9.A
【分析】利用三角形法则求出,再根据三角形中心的性质解决问题即可.
【解析】解:∵,,
∴,
∵AD,BE是△ABC的中线,
∴G是△ABC的重心,
∴BG=BE,
∴=,
故选A.
10.B
【分析】根据平面向量的定义,平面向量模的定义以及共线向量的定义进行判断即可.
【解析】A.当单位概率与非零向量的方向相同时才成立,故该选项不正确,不符合题意;
B. ,故该选项正确,符合题意;
C.当非零向量,的方向相同时才成立,故该选项不正确,不符合题意;
D. 当单位概率与非零向量的方向相同时才成立,故该选项不正确,不符合题意;
故选B
二、填空题
11.
【分析】本题考查向量的加减运算,根据向量加减运算法则求解即可
【解析】解:
,
故答案为:.
12.
【分析】本题考查了平面向量的线性表示法,熟练掌握平面向量的性质是解题的关键.根据平面向量与单位向量方向相反,长度为7,即可得出结论.
【解析】解:∵向量和方向相反,长度为7,
∴.
故答案为: .
13.
【分析】本题主要考查了平面向量,先求出,再利用三角形法则求得答案.
【解析】解:∵,点D是的中点,
∴,
又∵,
∴,
故答案为:.
14.
【分析】本题考查了相似三角形的判定和性质,向量的定义.先根据,得,再根据相似三角形的性质及向量的定义即可,本题的关键是熟练掌握相似三角形的判定和性质.
【解析】解:,
,
,
,
,
,
故答案为:.
15.
【分析】如图,先根据向量的减法法则求出,根据D点是边的中点求出,再由向量的加法法则求出,然后根据G是 ABC的重心即可求出.
【解析】如图,D点是边的中点,G是 ABC的重心,
∵,,
∴
∵D点是边的中点,
∴,
∴,
∵G是的重心,
∴.
故答案为:.
16.
【分析】本题考查的知识点是向量的线性运算、平行四边形的性质,解题关键是熟练掌握向量的线性运算.
首先由四边形是平行四边形,求得,又由点是边中点,点是边上的点,且,求得与,再利用三角形法则求解即可.
【解析】解:四边形是平行四边形,
,
点是边中点,点是边上的点,且,
,,
.
故答案为:.
17.
【分析】本题考查了向量的运算,根据向量的相关运算法则计算即可.
【解析】解:,
故答案为:.
18.
【分析】根据翻折的性质、相似三角形的性质、相似三角形是判定及比例的性质求解.本题考查了翻折变换,掌握翻折的性质、相似三角形的性质、相似三角形是判定及比例的性质是解题的关键.
【解析】解:连接交于,交于点,
将沿直线翻折,点落在边上的点处,
,,
,
,
,
,
,
在中,,
,
,
,
∴
故答案为:.
三、解答题
19.(1)∵,
,
∴,
∴,即,
∴或(不符合题意,舍去),
∴的长为6;
(2)∵,
∴,
∴=,
∴.
20.(1)解:∵,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴
21.解:(1)点N和点A、B所构成的三角形与 ABC相似,理由如下:
设网格中小正方形的边长为a,
则BC=a,AB=, AC=,其中BC<AB<AC
如下图所示,连接BM、AM
则BM=,AM=,其中AB<BM<AM
∴,
∴≠
∴和 ABC不相似;
如下图所示,连接AN
则BN=2a,AN=,其中AB<BN<AN
∴,,,
∴==
∴∽ ABC;
如下图所示,连接BP
则BP=,AP=3,其中AB<BP<AP
∴,
∴≠
∴和 ABC不相似;
如下图所示,连接BQ、AQ
则BQ=,AQ=,其中AB<BQ<AQ
∴,
∴≠
∴和 ABC不相似;
综上:点N和点A、B所构成的三角形与 ABC相似;
(2)延长AB至E,使BE=AB,根据正方形的性质可知,点E正好落在格点上,如下图所示
∴,
∴=+
=.
22.(1)解: ,,,,
,
,
,
.
(2)解:由(1)中可知,
,
,
∴.
23.(1)解:∵四边形是平行四边形
∴,,
∴,,
∵
∴
∵
∴;
∵
∴
∴
∴,
∵
∴;
(2)如图,即为分别在、方向上的分向量.
24.(1)解:∵,
∴,,
∴ ABE∽ DCE,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
(2)由(1)得,则,
∵,
∴,
由(1)得,
∴,
则.
25.(1)解:,,
是的重心,联结并延长交于点,
为的边上的中线,
即点为的中点,
,
故答案为:.
(2)是的重心,
.
,,
,
26.解:(1)∵,
∵点G是Rt△ABC的重心,
∴AD=AC,
∵,,
∴,
∴
∴,
.
(2)∵G是三角形的重心,
∴BG=2GD,AD=DC,
∵BG=6,
∴GD=3,
∵,,
∴AG=GD=3,
∴,
∵,
∴,
∴DE=,
∴AE=AD+DE=
