江苏省泰州市兴化市2024-2025学年九年级下学期开学考试数学试题(图片版,含答案)
文档属性
| 名称 | 江苏省泰州市兴化市2024-2025学年九年级下学期开学考试数学试题(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 09:45:28 | ||
图片预览



文档简介
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
九年级期初数学评分标准
一、(每一题 3 分)
1-6 D C D A B B
二、(每一题 3 分)
2
7、 8、甲 9、9 10、6 5 11、 x 1或x 5
5
4 14
12、34 13、 y2 y3 y1 14、4 3 - π 15、 16、8- 4 2
3 5
三、
17、(本题满分 12分)
(1)解: x2 4x 4 3 4
2 (3 分) x 2 1
x 2 1或x 2 1
x 1或x 3 (6 分)
(2)解:原式 (9 分)
3
2- 3 2 -3
2
2 - 3 3 -3
-1 (12 分)
18、(本题满分 8分)
1
(1) (3 分)
3
(2)解:画树状图如下:(略)
∴一共有 9种等可能得结果,
其中小华获得 2份奖品结果有 1种
1
∴小华获得 2份奖品的概率为 .(8 分)
9
19、(本题满分 8分)
(1)解:400÷40%=1000(台)
答:三种型号的电风扇共 1000 台.(3 分)
(2 列式:1000-400-250=350(台)
画图:(5 分)
350
(3)解:5000× =1750(台)
1000
答:订购丙种型号电风扇 1750 台.(8 分)
20、(本题满分 8 分)
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
(1)(1)证明:连接 OP,如图 2,
∵PD 是⊙O 的切线,
∴OP⊥PD,
∵PD⊥BC,
∴OP∥BC,
∴∠OPA=∠C,
∵OA=OP,
∴∠OPA=∠A,
∴∠A=∠C;(4 分)
(2)解:连接 PB,如图 2,
在 Rt△PBD 中,∵PD=2BD=4,
∴PB= =2 ,
∵AB 为直径,
∴∠APB=90°,
∵∠BDP=∠BPC,∠DBP=∠PBC,
∴△BDP∽△BPC,
∴BP:BC=BD:BP,即 2 :BC=2:2 ,
解得 BC=10,
∵∠A=∠C,
∴BA=BC=10,
∴⊙O 的半径为 5.(8 分)
21、(本题满分 10分)
(1)证明:∵E是 AB的中点,DF FB ,
∴EF 是△ABD 的中位线
∴EF∥AD,(4 分)
(2)解:∵ EFB 90 ,
∴ CFB 180 90 90 ,
FB
tan FEB 3
在Rt△EFB 中, FE ,EF 1,
∴FB 3,
∵E是 AB的中点,DF FB
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
∴ AD 2EF 2,
∵四边形 AFCD为平行四边形,
∴CF AD 2,
∴在Rt△CFB中,由勾股定理得CB CF
2 FB2 13 .(10 分)
22、(本题满分 10分)
(1) 解:∵在Rt ABD 中
AB
tan 60
BD
∴ AB BD tan 60 10 3 10 3 m
∵在Rt ABC 中
AB
tan 45
BC
AB 10 3
∴ BC 10 3 m
tan 45 1
∴CD BC BD 10 3 10 m
即 CD 的长为 10 3 -10 m.(5 分)
(2)解:设 BD x m
∴ AB BD tan 60 3x
∴ BC AC 3x
∴ BC 3x x 5
∴1.7x x 5
∴ x 7.1
即 BD 的长为 7.1m.(10 分)
5 5( 3 1)
(说明:如求得 x= 6.8,得 10分)
3 1 2
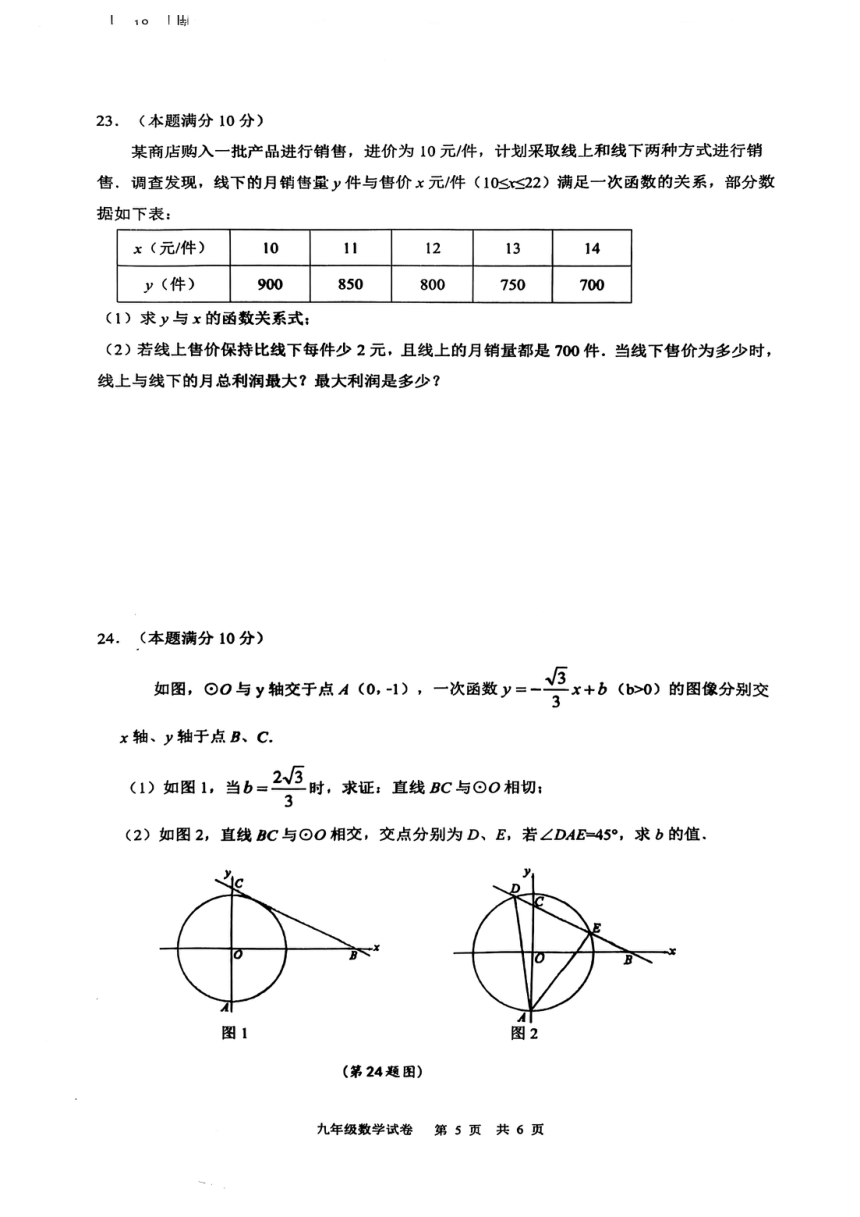
23、(本题满分 10分)
(1)解:设 y 与 x 的函数关系式为 y=kx+b(k≠0),
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
把(10,900),(11,850)代入解析式得 ,
解得 ,
∴y 与 x 的函数关系式为 y=﹣50x+1400(10≤x≤22);(4 分)
(2)解:设总利润为 w 元,
w=(x﹣10)(﹣50x+1400)+(x﹣2﹣10)×700
=﹣50x2+2600x﹣22400=﹣50(x﹣26)2+11400,(8 分)
∵﹣50<0,10≤x≤22,
∴当 x=22 时,w 取得最大值,此时 w=10600,
答:当线下销售为 22 元时,利润总和达到最大,最大利润是 10600 元.(10 分)
24、(本题满分 10分)
(1)证:过点 O 作 BC 的垂线,垂足为 D
3 2 3
∵ y x
3 3
2 3
∴C(0, ),B(2,0)
3
∴∠OBC=30°
∴OD=1
∵A(0,-1)
∴OA=OD=1
∴直线 BC 与⊙O 相切(5 分)
(2)解:连接 OD,OE,过点 O 作 BD 的垂线,垂足为 F
∵∠DOE=45°
∴∠DAE=90°
∵OD=OE
∴△DOE 为等腰直角三角形
OE 2
∴OF
2 2
∵∠OBC=30°
∴OB 20F 2
6
∴B( 2 ,0)代入直线中得 b=
3
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
6
即 b 的值为 (10 分)
3
25、(本题满分 12分)
(1)证:由正方形 ABCD 得:AB=AD,∠B=∠D=90°
由翻折得:AB=AF
∠AFE=∠B=90°
∴AD=AF,∠AFG=∠D=90°
∴Rt AFG∽Rt ADG
∴∠DAG=∠FAG(4 分)
(2)①解: 由(1)得:BE=EF=1,DG=FG
设 DG=FG=x
∴CE=1,CG=2-x
∵在 Rt CEG 中,由勾股定理得:
2 2 2
1+(2-x) =(x+1)
2 4
∴x= ∴CG=2-x=
3 3
CE 3
∴tan∠CGE=
CG 4
3
即 tan∠CGE 的值为 (8分)
4
(2)②解:连接 OE,过点 F 作直线 PQ⊥BC,分别交 BC、AD 于 P、 Q.
OF EP
易得 OE∥PQ∥CD,有 ,
OM EC
又 OE=CE=1
由(2)得:∠EFP=∠EGC
3
∴tan∠EFP=tan∠EGC=
4
设 EP=3x,FP=4x
2 2 2
∴(3x) +(4x) =1
1
∴ x
5
3
∴ EP
5
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
OF EP 3
∴
OM EC 5
OF 3
∴ (12分)
FM 2
26、(本题满分 14)
(1)解:∵ y kx 3经过点 C
∴令 x=0 得 y=-3
∴C(0,-3)
∴OC=3
4
∴ = =4
OB 3 OC
∴B(4,0),C(0,-3)在抛物线上
15
解得 b= ,c=-3
4
3 15
∴ y x2 x 3
4 4
∵B(4,0)在直线 y kx 3上
3
∴k=
4
3
∴ y x 3
4
3 2 15 3
即抛物线的解析式为 y x x 3,直线的解析式为 y x 3 .(4 分)
4 4 4
(2)方法一
解:过点 P 作 PQ∥y 轴交直线 BC 于点 Q
3 2 15
∵ y x x 3
4 4
令 y=0 得 x=1 或 x=4
∴A(1,0) B(4,0)
∴AB=3
1 1 9
∴S ABC AB yc 3 3
2 2 2
9
∴S BCP 2 9
2
3 2 15
设 P m, m m 3
4 4
3
∴Q m, m 3
4
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
3 3 2 15 ∴ PQ m 3 m m 3
4 4 4
3 2
m 3m
4
∴S BCP =S PQC S PQB
1
PQ xB xC
2
1 3 2
m 3m 4
2 4
3 2
m 6m
2
3
∴ m2 6m 9
2
∴m 2 10或m 2 10
即点 P 的横坐标为 x 2 10或x 2 - 10 (9 分)
方法二
解:过点 A 作 AD∥BC 交 y 轴于点 D
过点 P 作 PQ∥BC 交 y 轴于点 Q
3 3
∴AD: y x
4 4
3 9
∴OD= ,CD=
4 4
∵S BCP=2S ABC
9 9
∴CQ=2CD= 2 =
4 2
9 15 15
∴OQ 3 ,Q 0,
2 2 2
3 15
∴PQ: y x
4 4
与抛物线解析式联立方程组
解得: x 2 10或x 2 - 10
即点 P 的横坐标为 x 2 10或x 2 - 10 (9 分)
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
(2)解:作 PN⊥x 轴交 BC 于 N,过点 N 作 NE⊥y 轴交于 E,
3 2 15
设 P(m, - m m 3)
4 4
3 2
∴ PN m 3m
4
∵PN∥OC,
∴∠PNQ=∠OCB,
∴Rt△PQN∽Rt△BOC,
∴ = = ,
∵OB=4,OC=3,BC=5,
∴QN= PN,PQ= PN,
由△CNE∽△CBO,
∴CN= EN= m,
∴CQ+ PQ=CN+NQ+ PQ=CN+PN,
2
5 3 2 3 2 17 3 17 289 ∴CQ+ PQ= m m 3m m m m
4 4 4 4 4 6 48
17 289
∴当 m= 时,CQ+ PQ 的最大值是 .(14 分)
6 48
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
九年级期初数学评分标准
一、(每一题 3 分)
1-6 D C D A B B
二、(每一题 3 分)
2
7、 8、甲 9、9 10、6 5 11、 x 1或x 5
5
4 14
12、34 13、 y2 y3 y1 14、4 3 - π 15、 16、8- 4 2
3 5
三、
17、(本题满分 12分)
(1)解: x2 4x 4 3 4
2 (3 分) x 2 1
x 2 1或x 2 1
x 1或x 3 (6 分)
(2)解:原式 (9 分)
3
2- 3 2 -3
2
2 - 3 3 -3
-1 (12 分)
18、(本题满分 8分)
1
(1) (3 分)
3
(2)解:画树状图如下:(略)
∴一共有 9种等可能得结果,
其中小华获得 2份奖品结果有 1种
1
∴小华获得 2份奖品的概率为 .(8 分)
9
19、(本题满分 8分)
(1)解:400÷40%=1000(台)
答:三种型号的电风扇共 1000 台.(3 分)
(2 列式:1000-400-250=350(台)
画图:(5 分)
350
(3)解:5000× =1750(台)
1000
答:订购丙种型号电风扇 1750 台.(8 分)
20、(本题满分 8 分)
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
(1)(1)证明:连接 OP,如图 2,
∵PD 是⊙O 的切线,
∴OP⊥PD,
∵PD⊥BC,
∴OP∥BC,
∴∠OPA=∠C,
∵OA=OP,
∴∠OPA=∠A,
∴∠A=∠C;(4 分)
(2)解:连接 PB,如图 2,
在 Rt△PBD 中,∵PD=2BD=4,
∴PB= =2 ,
∵AB 为直径,
∴∠APB=90°,
∵∠BDP=∠BPC,∠DBP=∠PBC,
∴△BDP∽△BPC,
∴BP:BC=BD:BP,即 2 :BC=2:2 ,
解得 BC=10,
∵∠A=∠C,
∴BA=BC=10,
∴⊙O 的半径为 5.(8 分)
21、(本题满分 10分)
(1)证明:∵E是 AB的中点,DF FB ,
∴EF 是△ABD 的中位线
∴EF∥AD,(4 分)
(2)解:∵ EFB 90 ,
∴ CFB 180 90 90 ,
FB
tan FEB 3
在Rt△EFB 中, FE ,EF 1,
∴FB 3,
∵E是 AB的中点,DF FB
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
∴ AD 2EF 2,
∵四边形 AFCD为平行四边形,
∴CF AD 2,
∴在Rt△CFB中,由勾股定理得CB CF
2 FB2 13 .(10 分)
22、(本题满分 10分)
(1) 解:∵在Rt ABD 中
AB
tan 60
BD
∴ AB BD tan 60 10 3 10 3 m
∵在Rt ABC 中
AB
tan 45
BC
AB 10 3
∴ BC 10 3 m
tan 45 1
∴CD BC BD 10 3 10 m
即 CD 的长为 10 3 -10 m.(5 分)
(2)解:设 BD x m
∴ AB BD tan 60 3x
∴ BC AC 3x
∴ BC 3x x 5
∴1.7x x 5
∴ x 7.1
即 BD 的长为 7.1m.(10 分)
5 5( 3 1)
(说明:如求得 x= 6.8,得 10分)
3 1 2
23、(本题满分 10分)
(1)解:设 y 与 x 的函数关系式为 y=kx+b(k≠0),
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
把(10,900),(11,850)代入解析式得 ,
解得 ,
∴y 与 x 的函数关系式为 y=﹣50x+1400(10≤x≤22);(4 分)
(2)解:设总利润为 w 元,
w=(x﹣10)(﹣50x+1400)+(x﹣2﹣10)×700
=﹣50x2+2600x﹣22400=﹣50(x﹣26)2+11400,(8 分)
∵﹣50<0,10≤x≤22,
∴当 x=22 时,w 取得最大值,此时 w=10600,
答:当线下销售为 22 元时,利润总和达到最大,最大利润是 10600 元.(10 分)
24、(本题满分 10分)
(1)证:过点 O 作 BC 的垂线,垂足为 D
3 2 3
∵ y x
3 3
2 3
∴C(0, ),B(2,0)
3
∴∠OBC=30°
∴OD=1
∵A(0,-1)
∴OA=OD=1
∴直线 BC 与⊙O 相切(5 分)
(2)解:连接 OD,OE,过点 O 作 BD 的垂线,垂足为 F
∵∠DOE=45°
∴∠DAE=90°
∵OD=OE
∴△DOE 为等腰直角三角形
OE 2
∴OF
2 2
∵∠OBC=30°
∴OB 20F 2
6
∴B( 2 ,0)代入直线中得 b=
3
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
6
即 b 的值为 (10 分)
3
25、(本题满分 12分)
(1)证:由正方形 ABCD 得:AB=AD,∠B=∠D=90°
由翻折得:AB=AF
∠AFE=∠B=90°
∴AD=AF,∠AFG=∠D=90°
∴Rt AFG∽Rt ADG
∴∠DAG=∠FAG(4 分)
(2)①解: 由(1)得:BE=EF=1,DG=FG
设 DG=FG=x
∴CE=1,CG=2-x
∵在 Rt CEG 中,由勾股定理得:
2 2 2
1+(2-x) =(x+1)
2 4
∴x= ∴CG=2-x=
3 3
CE 3
∴tan∠CGE=
CG 4
3
即 tan∠CGE 的值为 (8分)
4
(2)②解:连接 OE,过点 F 作直线 PQ⊥BC,分别交 BC、AD 于 P、 Q.
OF EP
易得 OE∥PQ∥CD,有 ,
OM EC
又 OE=CE=1
由(2)得:∠EFP=∠EGC
3
∴tan∠EFP=tan∠EGC=
4
设 EP=3x,FP=4x
2 2 2
∴(3x) +(4x) =1
1
∴ x
5
3
∴ EP
5
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
OF EP 3
∴
OM EC 5
OF 3
∴ (12分)
FM 2
26、(本题满分 14)
(1)解:∵ y kx 3经过点 C
∴令 x=0 得 y=-3
∴C(0,-3)
∴OC=3
4
∴ = =4
OB 3 OC
∴B(4,0),C(0,-3)在抛物线上
15
解得 b= ,c=-3
4
3 15
∴ y x2 x 3
4 4
∵B(4,0)在直线 y kx 3上
3
∴k=
4
3
∴ y x 3
4
3 2 15 3
即抛物线的解析式为 y x x 3,直线的解析式为 y x 3 .(4 分)
4 4 4
(2)方法一
解:过点 P 作 PQ∥y 轴交直线 BC 于点 Q
3 2 15
∵ y x x 3
4 4
令 y=0 得 x=1 或 x=4
∴A(1,0) B(4,0)
∴AB=3
1 1 9
∴S ABC AB yc 3 3
2 2 2
9
∴S BCP 2 9
2
3 2 15
设 P m, m m 3
4 4
3
∴Q m, m 3
4
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
3 3 2 15 ∴ PQ m 3 m m 3
4 4 4
3 2
m 3m
4
∴S BCP =S PQC S PQB
1
PQ xB xC
2
1 3 2
m 3m 4
2 4
3 2
m 6m
2
3
∴ m2 6m 9
2
∴m 2 10或m 2 10
即点 P 的横坐标为 x 2 10或x 2 - 10 (9 分)
方法二
解:过点 A 作 AD∥BC 交 y 轴于点 D
过点 P 作 PQ∥BC 交 y 轴于点 Q
3 3
∴AD: y x
4 4
3 9
∴OD= ,CD=
4 4
∵S BCP=2S ABC
9 9
∴CQ=2CD= 2 =
4 2
9 15 15
∴OQ 3 ,Q 0,
2 2 2
3 15
∴PQ: y x
4 4
与抛物线解析式联立方程组
解得: x 2 10或x 2 - 10
即点 P 的横坐标为 x 2 10或x 2 - 10 (9 分)
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
(2)解:作 PN⊥x 轴交 BC 于 N,过点 N 作 NE⊥y 轴交于 E,
3 2 15
设 P(m, - m m 3)
4 4
3 2
∴ PN m 3m
4
∵PN∥OC,
∴∠PNQ=∠OCB,
∴Rt△PQN∽Rt△BOC,
∴ = = ,
∵OB=4,OC=3,BC=5,
∴QN= PN,PQ= PN,
由△CNE∽△CBO,
∴CN= EN= m,
∴CQ+ PQ=CN+NQ+ PQ=CN+PN,
2
5 3 2 3 2 17 3 17 289 ∴CQ+ PQ= m m 3m m m m
4 4 4 4 4 6 48
17 289
∴当 m= 时,CQ+ PQ 的最大值是 .(14 分)
6 48
{#{QQABIQQg4wqQgAZACA4aVUW0CQqQkIGRLWoOARAZKAQLgZNAFIA=}#}
同课章节目录
