代入法解二元一次方程组
图片预览



文档简介
课件10张PPT。复 习 由两个一次方程组成并含有两个未知数的方程组叫做二元一次方程组 方程组里各个方程的公共解叫做这个方程组的解二元一次方程组中各个方程的解一定是方程组的解 ( )
方程组的解一定是组成这个方程组的每一个方程的解 ( )判
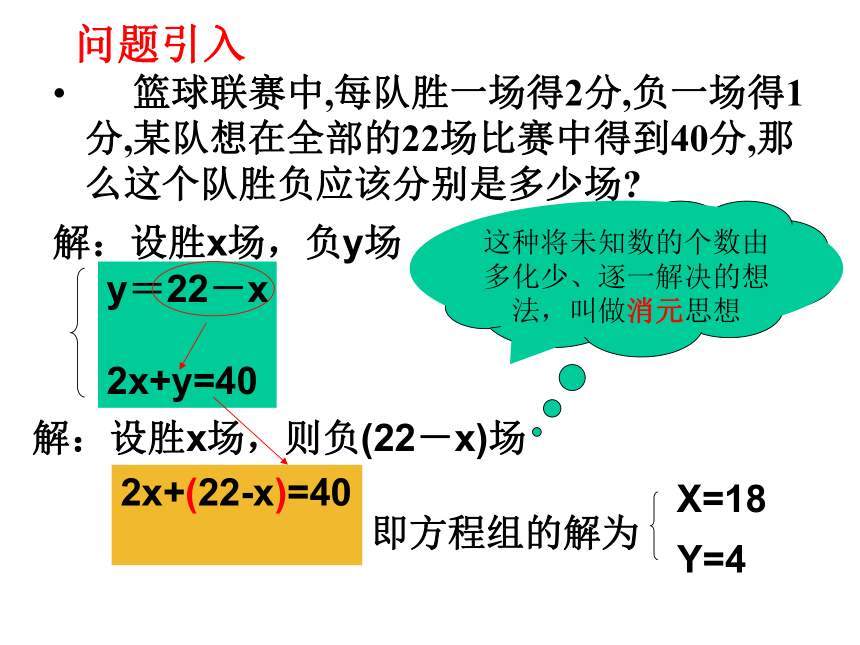
断错对用代入法解二元一次方程组(一) 篮球联赛中,每队胜一场得2分,负一场得1分,某队想在全部的22场比赛中得到40分,那么这个队胜负应该分别是多少场?问题引入解:设胜x场,负y场
解:设胜x场,则负(22-x)场
二元一次方程组和一元一次方程有什么关系 ?
y=22-x
2x+y=402x+(22-x)=40
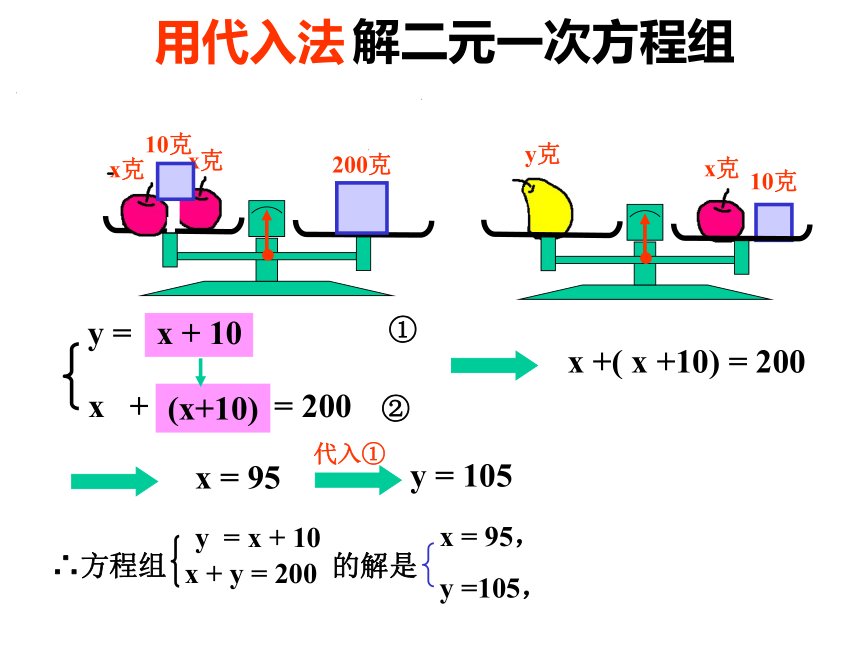
X=18Y=4这种将未知数的个数由多化少、逐一解决的想法,叫做消元思想即方程组的解为 x + y = 200y = x + 10解二元一次方程组用代入法x克10克(x+10)x +( x +10) = 200①②x = 95代入①y = 105上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法(substitution method)。归纳二
元
一
次
方
程
组x +y=222x+y=40y=18X=22解得x变形解得y代入消y归纳总结上面解方程组的过程可以用下面的框图表示:用 y=22-x 代替y,消未知数y
2x+(22-x)=40y=22-x例1 解方程组3x+2y = 14 x = y +33x+2 y = 1x = y +3例2 解方程组解:①②由②得:x = 13 – 4y③把③代入①得:2(13-4y)+ 3y= 1626-8y+3y=16-8y+3y=16-26-5y= -10y = 2把y = 2代入③,得x = 13 – 4y= 13-8= 5∴x = 2y = 51、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解实战演练 解方程组④小结1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解
方程组的解一定是组成这个方程组的每一个方程的解 ( )判
断错对用代入法解二元一次方程组(一) 篮球联赛中,每队胜一场得2分,负一场得1分,某队想在全部的22场比赛中得到40分,那么这个队胜负应该分别是多少场?问题引入解:设胜x场,负y场
解:设胜x场,则负(22-x)场
二元一次方程组和一元一次方程有什么关系 ?
y=22-x
2x+y=402x+(22-x)=40
X=18Y=4这种将未知数的个数由多化少、逐一解决的想法,叫做消元思想即方程组的解为 x + y = 200y = x + 10解二元一次方程组用代入法x克10克(x+10)x +( x +10) = 200①②x = 95代入①y = 105上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法(substitution method)。归纳二
元
一
次
方
程
组x +y=222x+y=40y=18X=22解得x变形解得y代入消y归纳总结上面解方程组的过程可以用下面的框图表示:用 y=22-x 代替y,消未知数y
2x+(22-x)=40y=22-x例1 解方程组3x+2y = 14 x = y +33x+2 y = 1x = y +3例2 解方程组解:①②由②得:x = 13 – 4y③把③代入①得:2(13-4y)+ 3y= 1626-8y+3y=16-8y+3y=16-26-5y= -10y = 2把y = 2代入③,得x = 13 – 4y= 13-8= 5∴x = 2y = 51、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解实战演练 解方程组④小结1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值3、把这个未知数的值代入一次式,求得另一个未知数的值4、写出方程组的解
