9.1.1 生活中的轴对称 练习(含答案)2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.1.1 生活中的轴对称 练习(含答案)2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 19:53:09 | ||
图片预览


文档简介
9.1 轴对称
1.生活中的轴对称
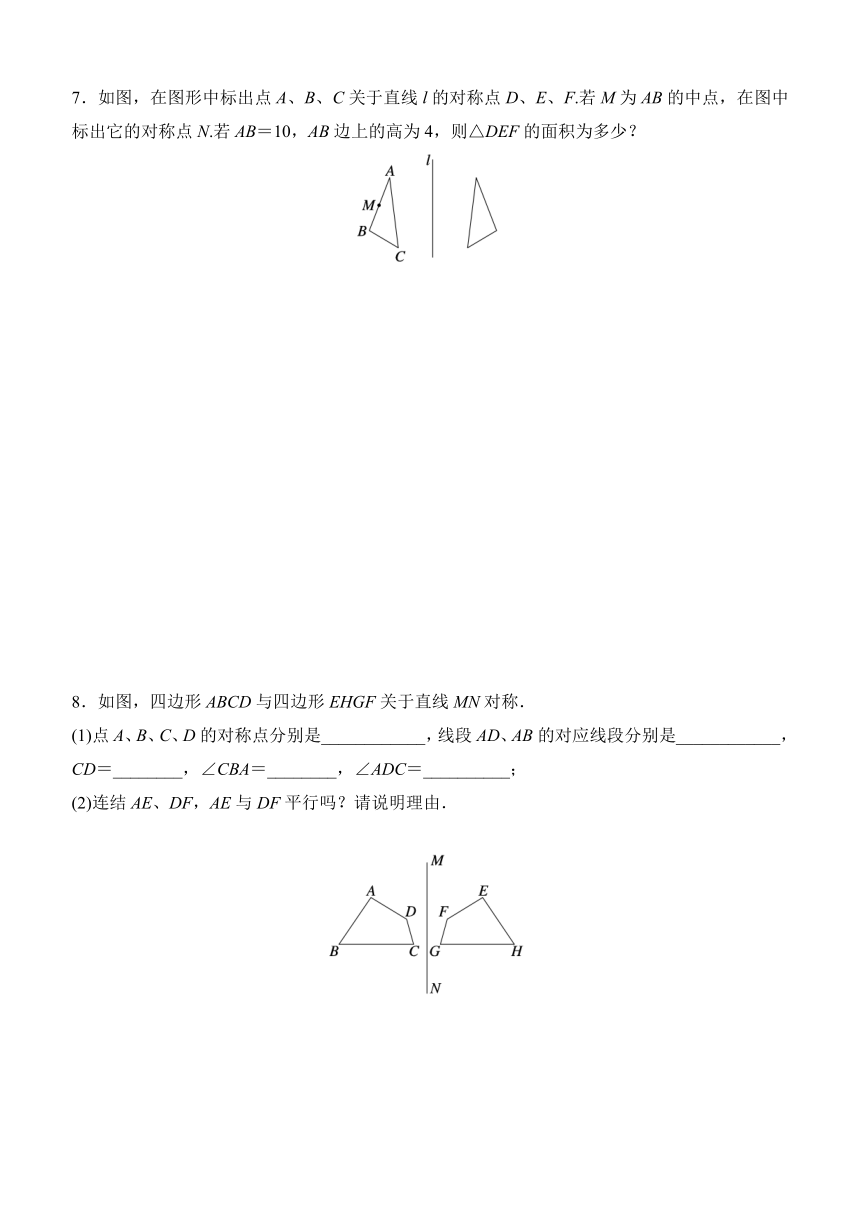
1.(2024巴中中考)下列图形中,是轴对称图形的是( )
2.(2024重庆B卷中考)下列标点符号中,是轴对称图形的是( )
3.(2024扬州江都区月考)如图所示的轴对称图形有________条对称轴.
4.将一张长方形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
5.观察下列各组图形,其中成轴对称的是________.(只填序号)
6.如图,四边形ABCD是轴对称图形,AC所在的直线是它的对称轴,若∠BCD=70°,则∠ACB的度数为________.
7.如图,D、E分别是AB、AC上两点,点A与点A′关于直线DE成轴对称,DA′∥BC,∠A=34°,∠CEA′=54°,则∠BDA′=________°.
1.(2024武汉中考)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A. B. C. D.
2.剪纸是我国传统的民间艺术.将一张纸片按图中①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A. B. C. D.
3.若△ABC与△A′B′C′关于直线l对称,且∠A=40°,∠B′=80°,则∠C′=________°.
4.(2024甘肃中考)围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点________的位置,则所得的对弈图是轴对称图形.(填写A、B、C、D中的一处即可,A、B、C、D位于棋盘的格点上)
5.(2024达州通川区期末)如果一个正多边形的外角等于72°,那么这个正多边形共有________条对称轴.
6.如图,在△ABC中,∠A=32°,∠B=36°,点D是边AB上一点,点B关于直线CD的对称点为B′,当B′D∥AC时,∠BCD的度数为________.
7.如图,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
8.如图,四边形ABCD与四边形EHGF关于直线MN对称.
(1)点A、B、C、D的对称点分别是____________,线段AD、AB的对应线段分别是____________,CD=________,∠CBA=________,∠ADC=__________;
(2)连结AE、DF,AE与DF平行吗?请说明理由.
9.(几何直观)如图,直角三角形ABC的三个顶点A、B、C关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8 cm,A′C=12 cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
【详解答案】
课堂达标
1.D 2.A 3.4 4.C
5.①②④ 6.35° 7.122
课后提升
1.C 解析:A、B、D选项中的汉字都不能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以不是轴对称图形.C选项中的汉字能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以是轴对称图形.故选C.
2.A 解析:按照题图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个等腰直角三角形,展开后实际是从原纸片的四边处各剪去一个直角三角形,从原纸片的中心剪去一个正方形.故选A.
3.60 解析:∵△ABC与△A′B′C′关于直线l对称,∴∠A=∠A′=40°.∵∠B′=80°,∴∠C′=180°-∠B′-∠A′=60°.
4.A或C 解析:白方如果落子于点A或C的位置,那么所得的对弈图是轴对称图形.
5.5 解析:∵正多边形的外角和为360°,
∴这个正多边形的边数=360°÷72°=5,正五边形共有5条对称轴.
6.38° 解析:∵B′D∥AC,
∴∠ADB′=∠A=32°.
∴∠BDB′=180°-∠ADB′=148°.
∵点B关于直线CD的对称点为B′,
∴∠CDB′=∠CDB=×(360°-∠BDB′)=106°.
∴∠BCD=180°-∠B-∠CDB=38°.
7.解:点D、E、F、N如图所示.
由轴对称的性质易得S△DEF=S△ABC=×10×4=20.
8.解:(1)E、H、G、F EF、EH GF ∠GHE ∠EFG
(2)AE∥DF.理由如下:
∵点A与点E是关于直线MN的对称点,点D与点F是关于直线MN的对称点,
∴MN垂直平分AE,MN垂直平分DF.
∴AE∥DF.
9.解:(1)∵直角三角形ABC的三个顶点A、B、C关于直线MN的对称点分别为A′、B′、C′,AC=8 cm,A′C=12 cm,
∴AC=A′C′,BC=B′C′.
∴△A′B′C′的周长为A′C′+B′C′+A′B′=AC+A′C=8+12=20(cm).
(2)如图,连结CC′,由(1),得△A′CC′的面积为A′C·A′C′=×12×8=48(cm2).
1.生活中的轴对称
1.(2024巴中中考)下列图形中,是轴对称图形的是( )
2.(2024重庆B卷中考)下列标点符号中,是轴对称图形的是( )
3.(2024扬州江都区月考)如图所示的轴对称图形有________条对称轴.
4.将一张长方形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
5.观察下列各组图形,其中成轴对称的是________.(只填序号)
6.如图,四边形ABCD是轴对称图形,AC所在的直线是它的对称轴,若∠BCD=70°,则∠ACB的度数为________.
7.如图,D、E分别是AB、AC上两点,点A与点A′关于直线DE成轴对称,DA′∥BC,∠A=34°,∠CEA′=54°,则∠BDA′=________°.
1.(2024武汉中考)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A. B. C. D.
2.剪纸是我国传统的民间艺术.将一张纸片按图中①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A. B. C. D.
3.若△ABC与△A′B′C′关于直线l对称,且∠A=40°,∠B′=80°,则∠C′=________°.
4.(2024甘肃中考)围棋起源于中国,古代称为“弈”.如图是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点________的位置,则所得的对弈图是轴对称图形.(填写A、B、C、D中的一处即可,A、B、C、D位于棋盘的格点上)
5.(2024达州通川区期末)如果一个正多边形的外角等于72°,那么这个正多边形共有________条对称轴.
6.如图,在△ABC中,∠A=32°,∠B=36°,点D是边AB上一点,点B关于直线CD的对称点为B′,当B′D∥AC时,∠BCD的度数为________.
7.如图,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
8.如图,四边形ABCD与四边形EHGF关于直线MN对称.
(1)点A、B、C、D的对称点分别是____________,线段AD、AB的对应线段分别是____________,CD=________,∠CBA=________,∠ADC=__________;
(2)连结AE、DF,AE与DF平行吗?请说明理由.
9.(几何直观)如图,直角三角形ABC的三个顶点A、B、C关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8 cm,A′C=12 cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
【详解答案】
课堂达标
1.D 2.A 3.4 4.C
5.①②④ 6.35° 7.122
课后提升
1.C 解析:A、B、D选项中的汉字都不能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以不是轴对称图形.C选项中的汉字能找到一条直线,使图形沿这条直线折叠,直线两旁的部分互相重合,所以是轴对称图形.故选C.
2.A 解析:按照题图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个等腰直角三角形,展开后实际是从原纸片的四边处各剪去一个直角三角形,从原纸片的中心剪去一个正方形.故选A.
3.60 解析:∵△ABC与△A′B′C′关于直线l对称,∴∠A=∠A′=40°.∵∠B′=80°,∴∠C′=180°-∠B′-∠A′=60°.
4.A或C 解析:白方如果落子于点A或C的位置,那么所得的对弈图是轴对称图形.
5.5 解析:∵正多边形的外角和为360°,
∴这个正多边形的边数=360°÷72°=5,正五边形共有5条对称轴.
6.38° 解析:∵B′D∥AC,
∴∠ADB′=∠A=32°.
∴∠BDB′=180°-∠ADB′=148°.
∵点B关于直线CD的对称点为B′,
∴∠CDB′=∠CDB=×(360°-∠BDB′)=106°.
∴∠BCD=180°-∠B-∠CDB=38°.
7.解:点D、E、F、N如图所示.
由轴对称的性质易得S△DEF=S△ABC=×10×4=20.
8.解:(1)E、H、G、F EF、EH GF ∠GHE ∠EFG
(2)AE∥DF.理由如下:
∵点A与点E是关于直线MN的对称点,点D与点F是关于直线MN的对称点,
∴MN垂直平分AE,MN垂直平分DF.
∴AE∥DF.
9.解:(1)∵直角三角形ABC的三个顶点A、B、C关于直线MN的对称点分别为A′、B′、C′,AC=8 cm,A′C=12 cm,
∴AC=A′C′,BC=B′C′.
∴△A′B′C′的周长为A′C′+B′C′+A′B′=AC+A′C=8+12=20(cm).
(2)如图,连结CC′,由(1),得△A′CC′的面积为A′C·A′C′=×12×8=48(cm2).
