9.2.2 平移的特征 练习(含答案)2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.2.2 平移的特征 练习(含答案)2024-2025学年数学华东师大版七年级下册 | 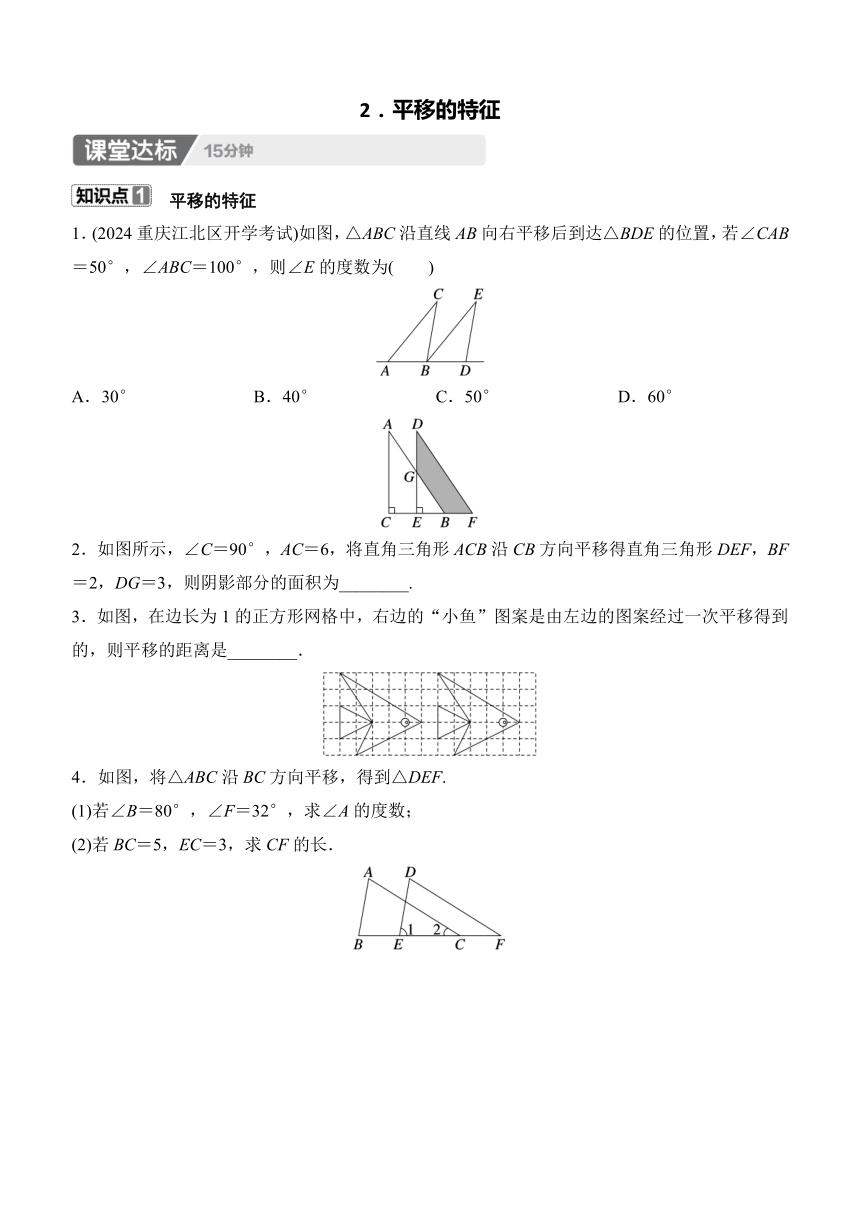 | |
| 格式 | docx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 19:55:24 | ||
图片预览


文档简介
2.平移的特征
1.(2024重庆江北区开学考试)如图,△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠E的度数为( )
A.30° B.40° C.50° D.60°
2.如图所示,∠C=90°,AC=6,将直角三角形ACB沿CB方向平移得直角三角形DEF,BF=2,DG=3,则阴影部分的面积为________.
3.如图,在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是________.
4.如图,将△ABC沿BC方向平移,得到△DEF.
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
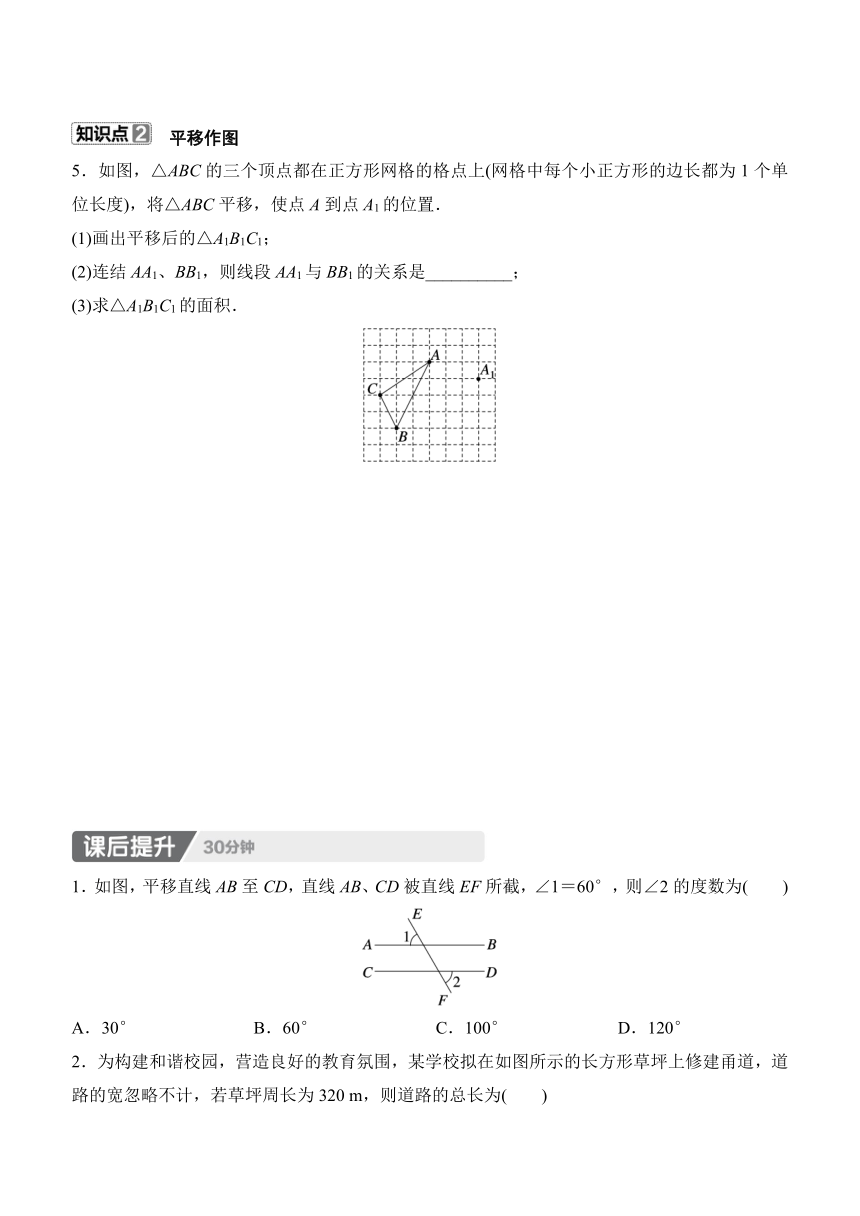
5.如图,△ABC的三个顶点都在正方形网格的格点上(网格中每个小正方形的边长都为1个单位长度),将△ABC平移,使点A到点A1的位置.
(1)画出平移后的△A1B1C1;
(2)连结AA1、BB1,则线段AA1与BB1的关系是__________;
(3)求△A1B1C1的面积.
1.如图,平移直线AB至CD,直线AB、CD被直线EF所截,∠1=60°,则∠2的度数为( )
A.30° B.60° C.100° D.120°
2.为构建和谐校园,营造良好的教育氛围,某学校拟在如图所示的长方形草坪上修建甬道,道路的宽忽略不计,若草坪周长为320 m,则道路的总长为( )
A.120 m B.160 m
C.240 m D.320 m
3.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=________°.
4.把边长分别为4和2的两个正方形A、B如图放置,把正方形B沿着水平方向向左平移,正方形A固定不动,当两个正方形重叠部分的面积为正方形B面积的时,此时平移的距离是________.
5.(教材P133例变式)如图,在方格纸中,每个小正方形的边长均为1个单位长度.△ABC的三个顶点均与小正方形的顶点重合.
(1)将△ABC先向右平移4个单位长度,再向下平移1个单位长度得到△DEF(A、B、C的对应点分别为D、E、F),请在方格纸中画出△DEF;
(2)若EM是△DEF的中线,求△DEM的面积.
6.如图,将周长为10的三角形ABC沿BC方向平移1个单位长度后得到三角形DEF,求四边形ABFD的周长.
7.(几何直观)如图,平面内点A、B沿同一方向平移相同距离分别得到点C、D,连结AB、BC,延长AC到点E,连结BE、DE,BC恰好平分∠ABE.
(1)若∠ACB=100°,∠CBE=40°,求∠EBD的度数;
(2)若∠AED=∠ABC+∠EBD,试说明:BC∥DE.
【详解答案】
课堂达标
1.A 2.9 3.6
4.解:(1)∵△DEF由△ABC沿BC方向平移得到,
∴∠2=∠F=32°.
又∵∠B=80°,
∴∠A=180°-32°-80°=68°.
(2)由平移可知,EF=BC,
∴EF-EC=BC-EC,
即CF=BE.
又∵BC=5,EC=3,
∴BE=BC-EC=5-3=2.
∴CF=BE=2.
5.解:(1)如图所示,△A1B1C1即
为所求.
(2)平行且相等
(3)△A1B1C1的面积为3×4-×2×3-×1×2-×2×4=4.
课后提升
1.B 解析:如图,
∵平移直线AB至CD,
∴AB∥CD.
∴∠BMF=∠2.
∵∠BMF=∠1=60°,
∴∠2=60°.故选B.
2.B 解析:∵长方形草坪周长为320 m,∴长方形的长和宽(一组邻边)之和为160 m.由平移知道路的总长等于长方形一组邻边长之和,
∴道路的总长为160 m.故选B.
3.110
解析:反向延长∠2的一边交直线b于点A,如图.∵直线a平移后得到直线b,∴a∥b.∴∠5=180°-∠1=180°-70°=110°.∵∠2=∠4+∠5,∠3=∠4,
∴∠2-∠3=∠5=110°.
4.或 解析:由题意可知:重叠部分的面积是2×2×=1,重叠部分的一边长是2,相邻边长是1 ÷2=,如图1,当正方形B在正方形A右侧时,正方形B平移的距离是,
图1
如图2,当正方形B在正方形A左侧时,正方形B平移的距离是4-+2=.
图2
故平移的距离是或.
5.解:(1)如图,△DEF即为所求.
(2)S△DEF=2×4-×1×2-×1×4-×2×2=8-1-2-2=3.
∵EM是△DEF的中线,
∴S△DEM=S△DEF=×3=.
6.解:由平移的性质可知BC=EF,AC=DF,AD=BE=1.
∵△ABC的周长为10,
∴AB+BC+AC=10.
∴AB+EF+DF=10.
∴四边形ABFD的周长=AB+EF+DF+AD+BE=12.
7.解:(1)由平移的性质可知AC∥BD,
∴∠CBD=∠ACB=100°.
∵∠CBE=40°,
∴∠EBD=∠CBD-∠CBE=100°-40°=60°.
(2)∵BC平分∠ABE,
∴∠ABC=∠EBC.
∵∠AED=∠ABC+∠EBD,
∴∠AED=∠EBC+∠EBD=∠CBD.
∵∠CBD=∠ACB,
∴∠AED=∠ACB.
∴BC∥DE.
1.(2024重庆江北区开学考试)如图,△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠E的度数为( )
A.30° B.40° C.50° D.60°
2.如图所示,∠C=90°,AC=6,将直角三角形ACB沿CB方向平移得直角三角形DEF,BF=2,DG=3,则阴影部分的面积为________.
3.如图,在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是________.
4.如图,将△ABC沿BC方向平移,得到△DEF.
(1)若∠B=80°,∠F=32°,求∠A的度数;
(2)若BC=5,EC=3,求CF的长.
5.如图,△ABC的三个顶点都在正方形网格的格点上(网格中每个小正方形的边长都为1个单位长度),将△ABC平移,使点A到点A1的位置.
(1)画出平移后的△A1B1C1;
(2)连结AA1、BB1,则线段AA1与BB1的关系是__________;
(3)求△A1B1C1的面积.
1.如图,平移直线AB至CD,直线AB、CD被直线EF所截,∠1=60°,则∠2的度数为( )
A.30° B.60° C.100° D.120°
2.为构建和谐校园,营造良好的教育氛围,某学校拟在如图所示的长方形草坪上修建甬道,道路的宽忽略不计,若草坪周长为320 m,则道路的总长为( )
A.120 m B.160 m
C.240 m D.320 m
3.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=________°.
4.把边长分别为4和2的两个正方形A、B如图放置,把正方形B沿着水平方向向左平移,正方形A固定不动,当两个正方形重叠部分的面积为正方形B面积的时,此时平移的距离是________.
5.(教材P133例变式)如图,在方格纸中,每个小正方形的边长均为1个单位长度.△ABC的三个顶点均与小正方形的顶点重合.
(1)将△ABC先向右平移4个单位长度,再向下平移1个单位长度得到△DEF(A、B、C的对应点分别为D、E、F),请在方格纸中画出△DEF;
(2)若EM是△DEF的中线,求△DEM的面积.
6.如图,将周长为10的三角形ABC沿BC方向平移1个单位长度后得到三角形DEF,求四边形ABFD的周长.
7.(几何直观)如图,平面内点A、B沿同一方向平移相同距离分别得到点C、D,连结AB、BC,延长AC到点E,连结BE、DE,BC恰好平分∠ABE.
(1)若∠ACB=100°,∠CBE=40°,求∠EBD的度数;
(2)若∠AED=∠ABC+∠EBD,试说明:BC∥DE.
【详解答案】
课堂达标
1.A 2.9 3.6
4.解:(1)∵△DEF由△ABC沿BC方向平移得到,
∴∠2=∠F=32°.
又∵∠B=80°,
∴∠A=180°-32°-80°=68°.
(2)由平移可知,EF=BC,
∴EF-EC=BC-EC,
即CF=BE.
又∵BC=5,EC=3,
∴BE=BC-EC=5-3=2.
∴CF=BE=2.
5.解:(1)如图所示,△A1B1C1即
为所求.
(2)平行且相等
(3)△A1B1C1的面积为3×4-×2×3-×1×2-×2×4=4.
课后提升
1.B 解析:如图,
∵平移直线AB至CD,
∴AB∥CD.
∴∠BMF=∠2.
∵∠BMF=∠1=60°,
∴∠2=60°.故选B.
2.B 解析:∵长方形草坪周长为320 m,∴长方形的长和宽(一组邻边)之和为160 m.由平移知道路的总长等于长方形一组邻边长之和,
∴道路的总长为160 m.故选B.
3.110
解析:反向延长∠2的一边交直线b于点A,如图.∵直线a平移后得到直线b,∴a∥b.∴∠5=180°-∠1=180°-70°=110°.∵∠2=∠4+∠5,∠3=∠4,
∴∠2-∠3=∠5=110°.
4.或 解析:由题意可知:重叠部分的面积是2×2×=1,重叠部分的一边长是2,相邻边长是1 ÷2=,如图1,当正方形B在正方形A右侧时,正方形B平移的距离是,
图1
如图2,当正方形B在正方形A左侧时,正方形B平移的距离是4-+2=.
图2
故平移的距离是或.
5.解:(1)如图,△DEF即为所求.
(2)S△DEF=2×4-×1×2-×1×4-×2×2=8-1-2-2=3.
∵EM是△DEF的中线,
∴S△DEM=S△DEF=×3=.
6.解:由平移的性质可知BC=EF,AC=DF,AD=BE=1.
∵△ABC的周长为10,
∴AB+BC+AC=10.
∴AB+EF+DF=10.
∴四边形ABFD的周长=AB+EF+DF+AD+BE=12.
7.解:(1)由平移的性质可知AC∥BD,
∴∠CBD=∠ACB=100°.
∵∠CBE=40°,
∴∠EBD=∠CBD-∠CBE=100°-40°=60°.
(2)∵BC平分∠ABE,
∴∠ABC=∠EBC.
∵∠AED=∠ABC+∠EBD,
∴∠AED=∠EBC+∠EBD=∠CBD.
∵∠CBD=∠ACB,
∴∠AED=∠ACB.
∴BC∥DE.
