9.3.2 旋转的特征 练习(含答案)2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.3.2 旋转的特征 练习(含答案)2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 19:59:13 | ||
图片预览


文档简介
2.旋转的特征
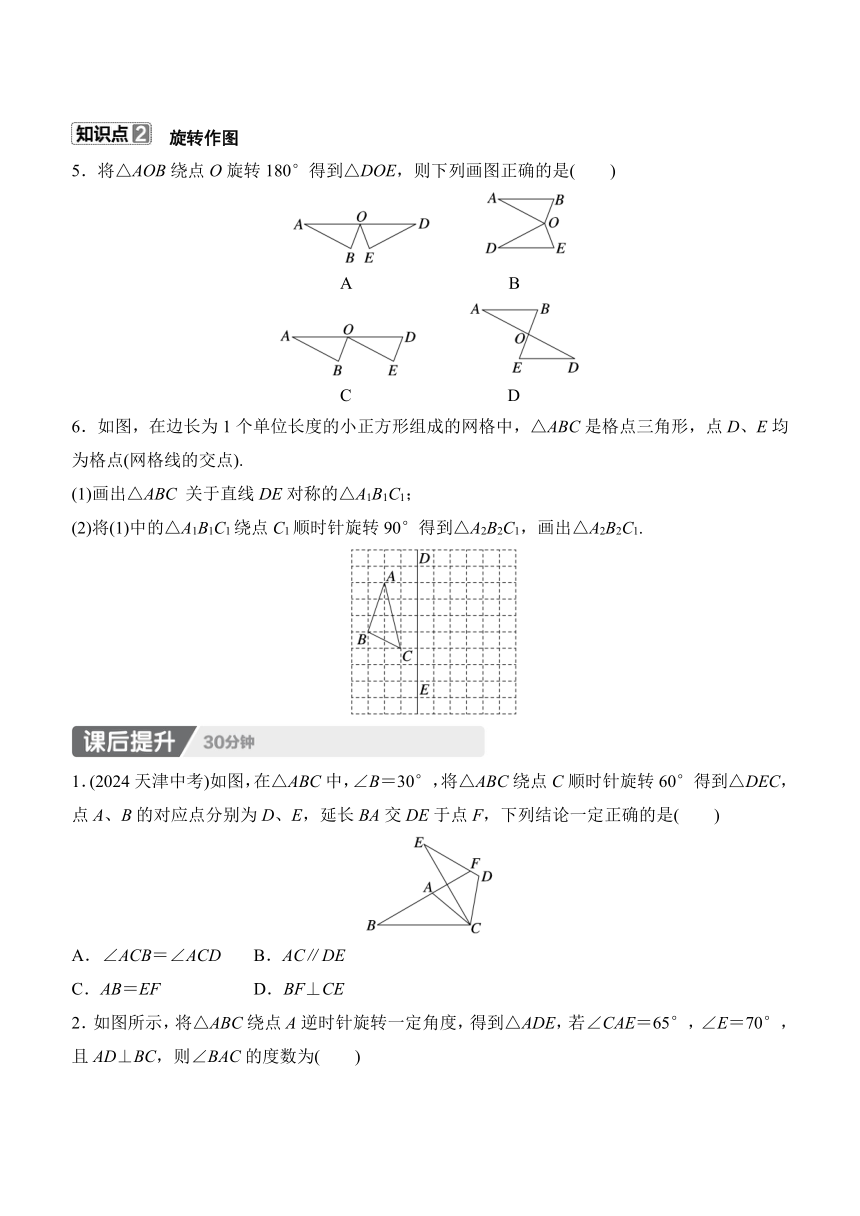
1.(2024无锡中考)如图,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB′C′.当AB′落在AC上时,∠BAC′的度数为( )
A.65° B.70° C.80° D.85°
2.(2024滨州中考)一副三角板如图1摆放,把三角板AOB绕公共顶点O顺时针旋转至图2,即AB∥OD时,∠1的大小为________°.
图1 图2
3.如图,将木条a、b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是________.
4.如图,在△ABC中,∠C=90°,∠ABC=50°.将△ABC绕点B按逆时针方向旋转得△DBE,使点E落在AB边上,点A的对应点为点D,连结AD,求∠ADE的度数.(注:等腰三角形的两个底角相等)
5.将△AOB绕点O旋转180°得到△DOE,则下列画图正确的是( )
A B
C D
6.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC是格点三角形,点D、E均为格点(网格线的交点).
(1)画出△ABC 关于直线DE对称的△A1B1C1;
(2)将(1)中的△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,画出△A2B2C1.
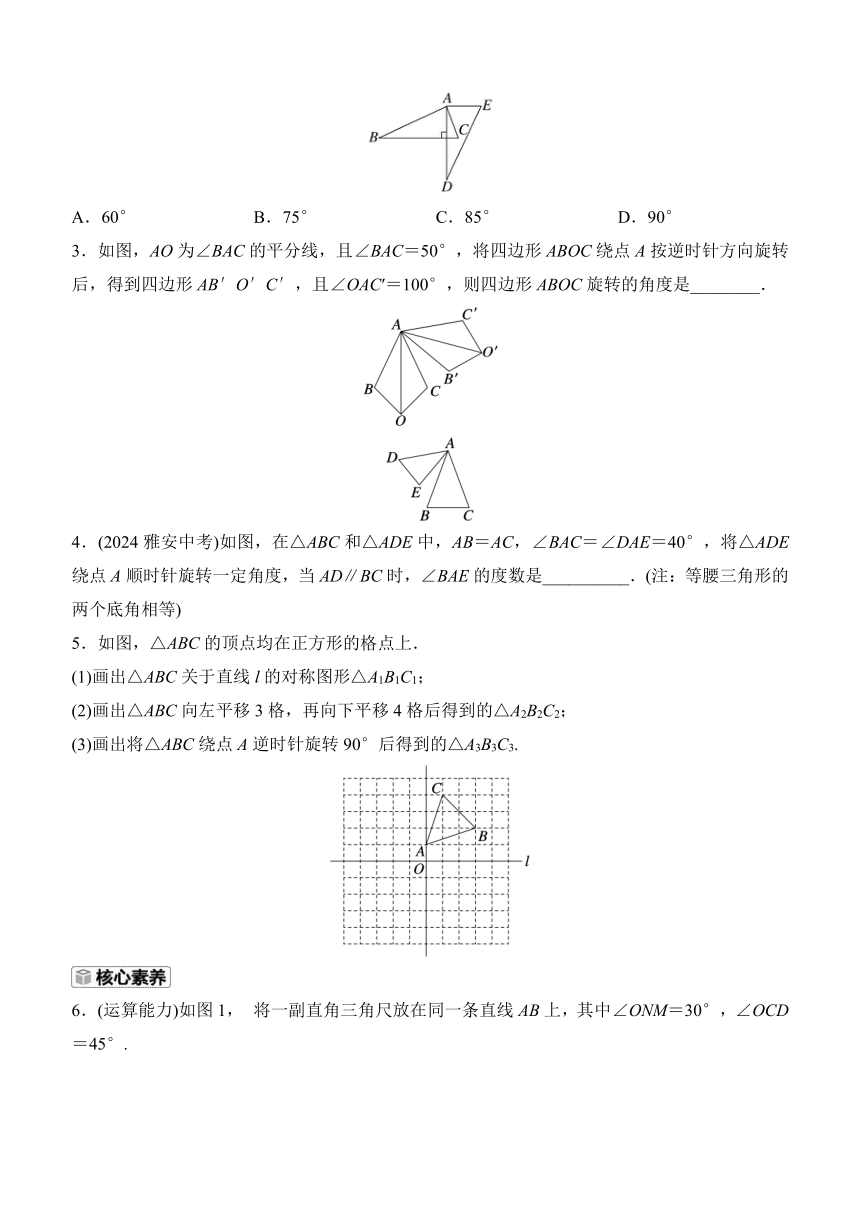
1.(2024天津中考)如图,在△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别为D、E,延长BA交DE于点F,下列结论一定正确的是( )
A.∠ACB=∠ACD B.AC∥DE
C.AB=EF D.BF⊥CE
2.如图所示,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
A.60° B.75° C.85° D.90°
3.如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB′O′C′,且∠OAC′=100°,则四边形ABOC旋转的角度是________.
4.(2024雅安中考)如图,在△ABC和△ADE中,AB=AC,∠BAC=∠DAE=40°,将△ADE绕点A顺时针旋转一定角度,当AD∥BC时,∠BAE的度数是__________.(注:等腰三角形的两个底角相等)
5.如图,△ABC的顶点均在正方形的格点上.
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)画出△ABC向左平移3格,再向下平移4格后得到的△A2B2C2;
(3)画出将△ABC绕点A逆时针旋转90°后得到的△A3B3C3.
6.(运算能力)如图1, 将一副直角三角尺放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)观察猜想:将图1中的三角尺OCD沿AB的方向平移至图2的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN=________;
(2)操作探究:将图1中的三角尺OCD绕点O按顺时针方向旋转,使边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数;
(3)深化拓展:将图1中的三角尺OCD绕点O按顺时针方向旋转一周,在旋转的过程中,当边OC旋转多少度时,边CD恰好与边MN平行?
【详解答案】
课堂达标
1.B 2.75 3.35°
4.解:∵∠C=90°,∠ABC=50°,
∴∠CAB=40°.
∵△ABC绕点B顺时针旋转得到△DBE,点E恰好在AB上,
∴BA=BD,∠ABC=∠DBA=50°,∠EDB=∠CAB=40°.
∴∠BAD=∠ADB=×(180°-50°)=65°.
∴∠ADE=∠ADB-∠EDB=25°.
5.D
6.解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C1即为所求.
课后提升
1.D 解析:设BF与CE相交于点H,如图所示.
∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°.
∵∠B=30°,
∴在△BHC中,∠BHC=180°-∠BCE-∠B=90°.
∴BF⊥CE.故D选项正确.
设∠ACH=x°,
∴∠ACB=60°-x°.
∵∠B=30°,
∴∠EDC=∠BAC=180°-30°-(60°-x°)=90°+x°.
∴∠EDC+∠ACD=90°+x°+60°=150°+x°.
∵x°不一定等于30°,
∴∠EDC+∠ACD不一定等于180°.
∴AC∥DE不一定成立.故B选项不正确.
∵∠ACB=60°-x°,∠ACD=60°,x°不一定等于0°,
∴∠ACB=∠ACD不一定成立.故A选项不正确.
∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴AB=ED=EF+FD.
∴AB>EF.故C选项不正确.故选D.
2.C 解析:由旋转的特征,得∠BAD=∠CAE=65°,∠C=∠E=70°.又∵AD⊥BC,
∴∠DAC=90°-∠C=90°-70°=20°.∴∠BAC=∠BAD+∠DAC=65°+20°=85°.故选C.
3.75° 解析:∵AO为∠BAC的平分线,∠BAC=50°,∴∠BAO=∠OAC=25°.∵将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB′O′C′,∴∠BAC=∠B′AC′=50°,∠B′AO′=∠O′AC′=25°.
∴∠OAO′=∠OAC′-∠O′AC′=100°-25°=75°.
4.30°或150° 解析:当点D在点A的左侧时,如图1所示.
∵AB=AC,∠BAC=40°,
∴∠ABC=(180°-∠BAC)=70°.
∵AD∥BC,∴∠BAD=∠ABC=70°.
∴∠BAE=∠BAD-∠DAE=70°-40°=30°.
当点D在点A的右侧时,如图2所示.
∵AB=AC,∠BAC=40°,
∴∠ACB=(180°-∠BAC)=70°.
∵AD∥BC,
∴∠DAC=∠ACB=70°.
∴∠BAE=∠BAC+∠DAC+∠DAE=40°+70°+40°=150°.
∴当AD∥BC时,∠BAE的度数为30°或150°.
5.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,△A3B3C3即为所求.
6.解:(1)105°
(2)∵OD平分∠MON,
∴∠DON=∠MON=×90°=45°.
∴∠DON=∠D=45°.
∴CD∥AB.
∴∠CEN=180°-∠ONM=180°-30°=150°.
(3)如图1,CD在AB上方时,设OD与MN相交于点F.
∵CD∥MN,
∴∠OFM=∠D=45°.
∴∠NOD=∠OFM-∠ONM=45°-30°=15°.
∴∠AOC=180°-90°-15°=75°.
当CD在AB的下方时,设直线OM与CD相交于点F.
∵CD∥MN,
∴∠DFO=∠M=60°.
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转角度为75°+180°=255°.
综上所述,当边OC旋转75°或255°时,边CD恰好与边MN平行.
1.(2024无锡中考)如图,在△ABC中,∠B=80°,∠C=65°,将△ABC绕点A逆时针旋转得到△AB′C′.当AB′落在AC上时,∠BAC′的度数为( )
A.65° B.70° C.80° D.85°
2.(2024滨州中考)一副三角板如图1摆放,把三角板AOB绕公共顶点O顺时针旋转至图2,即AB∥OD时,∠1的大小为________°.
图1 图2
3.如图,将木条a、b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是________.
4.如图,在△ABC中,∠C=90°,∠ABC=50°.将△ABC绕点B按逆时针方向旋转得△DBE,使点E落在AB边上,点A的对应点为点D,连结AD,求∠ADE的度数.(注:等腰三角形的两个底角相等)
5.将△AOB绕点O旋转180°得到△DOE,则下列画图正确的是( )
A B
C D
6.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC是格点三角形,点D、E均为格点(网格线的交点).
(1)画出△ABC 关于直线DE对称的△A1B1C1;
(2)将(1)中的△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1,画出△A2B2C1.
1.(2024天津中考)如图,在△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A、B的对应点分别为D、E,延长BA交DE于点F,下列结论一定正确的是( )
A.∠ACB=∠ACD B.AC∥DE
C.AB=EF D.BF⊥CE
2.如图所示,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
A.60° B.75° C.85° D.90°
3.如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB′O′C′,且∠OAC′=100°,则四边形ABOC旋转的角度是________.
4.(2024雅安中考)如图,在△ABC和△ADE中,AB=AC,∠BAC=∠DAE=40°,将△ADE绕点A顺时针旋转一定角度,当AD∥BC时,∠BAE的度数是__________.(注:等腰三角形的两个底角相等)
5.如图,△ABC的顶点均在正方形的格点上.
(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)画出△ABC向左平移3格,再向下平移4格后得到的△A2B2C2;
(3)画出将△ABC绕点A逆时针旋转90°后得到的△A3B3C3.
6.(运算能力)如图1, 将一副直角三角尺放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)观察猜想:将图1中的三角尺OCD沿AB的方向平移至图2的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN=________;
(2)操作探究:将图1中的三角尺OCD绕点O按顺时针方向旋转,使边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数;
(3)深化拓展:将图1中的三角尺OCD绕点O按顺时针方向旋转一周,在旋转的过程中,当边OC旋转多少度时,边CD恰好与边MN平行?
【详解答案】
课堂达标
1.B 2.75 3.35°
4.解:∵∠C=90°,∠ABC=50°,
∴∠CAB=40°.
∵△ABC绕点B顺时针旋转得到△DBE,点E恰好在AB上,
∴BA=BD,∠ABC=∠DBA=50°,∠EDB=∠CAB=40°.
∴∠BAD=∠ADB=×(180°-50°)=65°.
∴∠ADE=∠ADB-∠EDB=25°.
5.D
6.解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C1即为所求.
课后提升
1.D 解析:设BF与CE相交于点H,如图所示.
∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°.
∵∠B=30°,
∴在△BHC中,∠BHC=180°-∠BCE-∠B=90°.
∴BF⊥CE.故D选项正确.
设∠ACH=x°,
∴∠ACB=60°-x°.
∵∠B=30°,
∴∠EDC=∠BAC=180°-30°-(60°-x°)=90°+x°.
∴∠EDC+∠ACD=90°+x°+60°=150°+x°.
∵x°不一定等于30°,
∴∠EDC+∠ACD不一定等于180°.
∴AC∥DE不一定成立.故B选项不正确.
∵∠ACB=60°-x°,∠ACD=60°,x°不一定等于0°,
∴∠ACB=∠ACD不一定成立.故A选项不正确.
∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴AB=ED=EF+FD.
∴AB>EF.故C选项不正确.故选D.
2.C 解析:由旋转的特征,得∠BAD=∠CAE=65°,∠C=∠E=70°.又∵AD⊥BC,
∴∠DAC=90°-∠C=90°-70°=20°.∴∠BAC=∠BAD+∠DAC=65°+20°=85°.故选C.
3.75° 解析:∵AO为∠BAC的平分线,∠BAC=50°,∴∠BAO=∠OAC=25°.∵将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB′O′C′,∴∠BAC=∠B′AC′=50°,∠B′AO′=∠O′AC′=25°.
∴∠OAO′=∠OAC′-∠O′AC′=100°-25°=75°.
4.30°或150° 解析:当点D在点A的左侧时,如图1所示.
∵AB=AC,∠BAC=40°,
∴∠ABC=(180°-∠BAC)=70°.
∵AD∥BC,∴∠BAD=∠ABC=70°.
∴∠BAE=∠BAD-∠DAE=70°-40°=30°.
当点D在点A的右侧时,如图2所示.
∵AB=AC,∠BAC=40°,
∴∠ACB=(180°-∠BAC)=70°.
∵AD∥BC,
∴∠DAC=∠ACB=70°.
∴∠BAE=∠BAC+∠DAC+∠DAE=40°+70°+40°=150°.
∴当AD∥BC时,∠BAE的度数为30°或150°.
5.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,△A3B3C3即为所求.
6.解:(1)105°
(2)∵OD平分∠MON,
∴∠DON=∠MON=×90°=45°.
∴∠DON=∠D=45°.
∴CD∥AB.
∴∠CEN=180°-∠ONM=180°-30°=150°.
(3)如图1,CD在AB上方时,设OD与MN相交于点F.
∵CD∥MN,
∴∠OFM=∠D=45°.
∴∠NOD=∠OFM-∠ONM=45°-30°=15°.
∴∠AOC=180°-90°-15°=75°.
当CD在AB的下方时,设直线OM与CD相交于点F.
∵CD∥MN,
∴∠DFO=∠M=60°.
在△DOF中,∠DOF=180°-∠D-∠DFO=180°-45°-60°=75°,
∴旋转角度为75°+180°=255°.
综上所述,当边OC旋转75°或255°时,边CD恰好与边MN平行.
