9.3.3 旋转对称图形 练习(含答案)2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.3.3 旋转对称图形 练习(含答案)2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 00:00:00 | ||
图片预览


文档简介
3.旋转对称图形
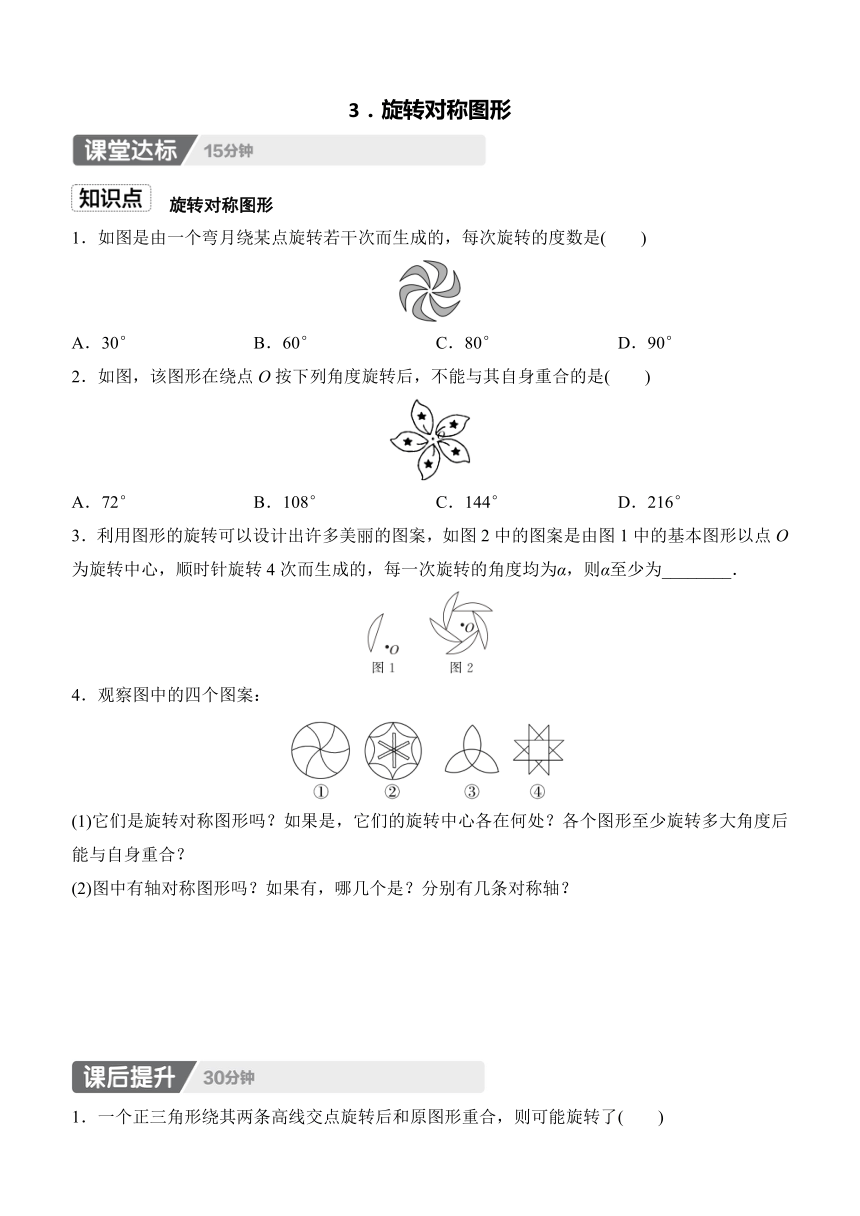
1.如图是由一个弯月绕某点旋转若干次而生成的,每次旋转的度数是( )
A.30° B.60° C.80° D.90°
2.如图,该图形在绕点O按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
3.利用图形的旋转可以设计出许多美丽的图案,如图2中的图案是由图1中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α,则α至少为________.
4.观察图中的四个图案:
(1)它们是旋转对称图形吗?如果是,它们的旋转中心各在何处?各个图形至少旋转多大角度后能与自身重合?
(2)图中有轴对称图形吗?如果有,哪几个是?分别有几条对称轴?
1.一个正三角形绕其两条高线交点旋转后和原图形重合,则可能旋转了( )
A.180° B.240° C.90° D.60°
2.观察如图所示的图形,绕着它的中心旋转120°后能与自身重合的有( )
A.1个 B.2个 C.3个 D.4个
3.如图是由中国结和雪花两种元素组成的一个图案,这个图案绕着它的旋转中心旋转角度α(0°<α<360°)后能够与它本身重合,则角度α最小是________°.
4.(几何直观)如图所示的风车图案绕点O旋转90°和180°都能和自身重合,四边形EFGH是正方形,且∠B=2∠BEF,试求∠A和∠AHG的度数.
【详解答案】
课堂达标
1.B 2.B 3.72°
4.解:(1)它们都是旋转对称图形,旋转中心为各自图形的中心.题图①至少旋转60°能与自身重合;题图②至少旋转60°能与自身重合;题图③至少旋转120°能与自身重合;题图④至少旋转90°能与自身重合.
(2)题图中有轴对称图形,题图②③④是轴对称图形;题图②有6条对称轴;题图③有3条对称轴;题图④有4条对称轴.
课后提升
1.B 解析:如图所示,
∵BE和CF分别是△ABC的高线,
∴∠EBC=∠FCB=30°.
∴∠BOC=180°-30°-30°=120°.
∴当△ABC绕点O旋转120°的整数倍的度数时,所得图形会和原图形重合,显然只有B选项符合题意.故选B.
2.B 解析:①旋转120°后,图形可以与原来的图形重合,故正确;②旋转120°后,图形无法与原来的图形重合,故错误;③旋转120°后,图形无法与原来的图形重合,故错误;④旋转120°后,图形可以与原来的图形重合,故正确.故选B.
3.60 解析:360°÷6=60°,则题中图案绕着它的中心旋转60°或60°的整数倍后能够与它本身重合,则α最小为60°.
4.解:∵四边形EFGH是正方形,
∴∠EFH=45°.
∵∠EFH=∠B+∠BEF,
∠B=2∠BEF,
∴∠EFH=2∠BEF+∠BEF=45°.
∴∠BEF=15°.
∴∠B=2∠BEF=30°.
∵∠B与∠A是对应角,
∴∠A=30°.
根据旋转的性质可知∠BEF=∠AHE,
∴∠AHE=15°.
∴∠AHG=15°+90°=105°.
1.如图是由一个弯月绕某点旋转若干次而生成的,每次旋转的度数是( )
A.30° B.60° C.80° D.90°
2.如图,该图形在绕点O按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
3.利用图形的旋转可以设计出许多美丽的图案,如图2中的图案是由图1中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α,则α至少为________.
4.观察图中的四个图案:
(1)它们是旋转对称图形吗?如果是,它们的旋转中心各在何处?各个图形至少旋转多大角度后能与自身重合?
(2)图中有轴对称图形吗?如果有,哪几个是?分别有几条对称轴?
1.一个正三角形绕其两条高线交点旋转后和原图形重合,则可能旋转了( )
A.180° B.240° C.90° D.60°
2.观察如图所示的图形,绕着它的中心旋转120°后能与自身重合的有( )
A.1个 B.2个 C.3个 D.4个
3.如图是由中国结和雪花两种元素组成的一个图案,这个图案绕着它的旋转中心旋转角度α(0°<α<360°)后能够与它本身重合,则角度α最小是________°.
4.(几何直观)如图所示的风车图案绕点O旋转90°和180°都能和自身重合,四边形EFGH是正方形,且∠B=2∠BEF,试求∠A和∠AHG的度数.
【详解答案】
课堂达标
1.B 2.B 3.72°
4.解:(1)它们都是旋转对称图形,旋转中心为各自图形的中心.题图①至少旋转60°能与自身重合;题图②至少旋转60°能与自身重合;题图③至少旋转120°能与自身重合;题图④至少旋转90°能与自身重合.
(2)题图中有轴对称图形,题图②③④是轴对称图形;题图②有6条对称轴;题图③有3条对称轴;题图④有4条对称轴.
课后提升
1.B 解析:如图所示,
∵BE和CF分别是△ABC的高线,
∴∠EBC=∠FCB=30°.
∴∠BOC=180°-30°-30°=120°.
∴当△ABC绕点O旋转120°的整数倍的度数时,所得图形会和原图形重合,显然只有B选项符合题意.故选B.
2.B 解析:①旋转120°后,图形可以与原来的图形重合,故正确;②旋转120°后,图形无法与原来的图形重合,故错误;③旋转120°后,图形无法与原来的图形重合,故错误;④旋转120°后,图形可以与原来的图形重合,故正确.故选B.
3.60 解析:360°÷6=60°,则题中图案绕着它的中心旋转60°或60°的整数倍后能够与它本身重合,则α最小为60°.
4.解:∵四边形EFGH是正方形,
∴∠EFH=45°.
∵∠EFH=∠B+∠BEF,
∠B=2∠BEF,
∴∠EFH=2∠BEF+∠BEF=45°.
∴∠BEF=15°.
∴∠B=2∠BEF=30°.
∵∠B与∠A是对应角,
∴∠A=30°.
根据旋转的性质可知∠BEF=∠AHE,
∴∠AHE=15°.
∴∠AHG=15°+90°=105°.
