9.4 中心对称 练习(含答案)2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.4 中心对称 练习(含答案)2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 00:00:00 | ||
图片预览

文档简介
9.4 中心对称
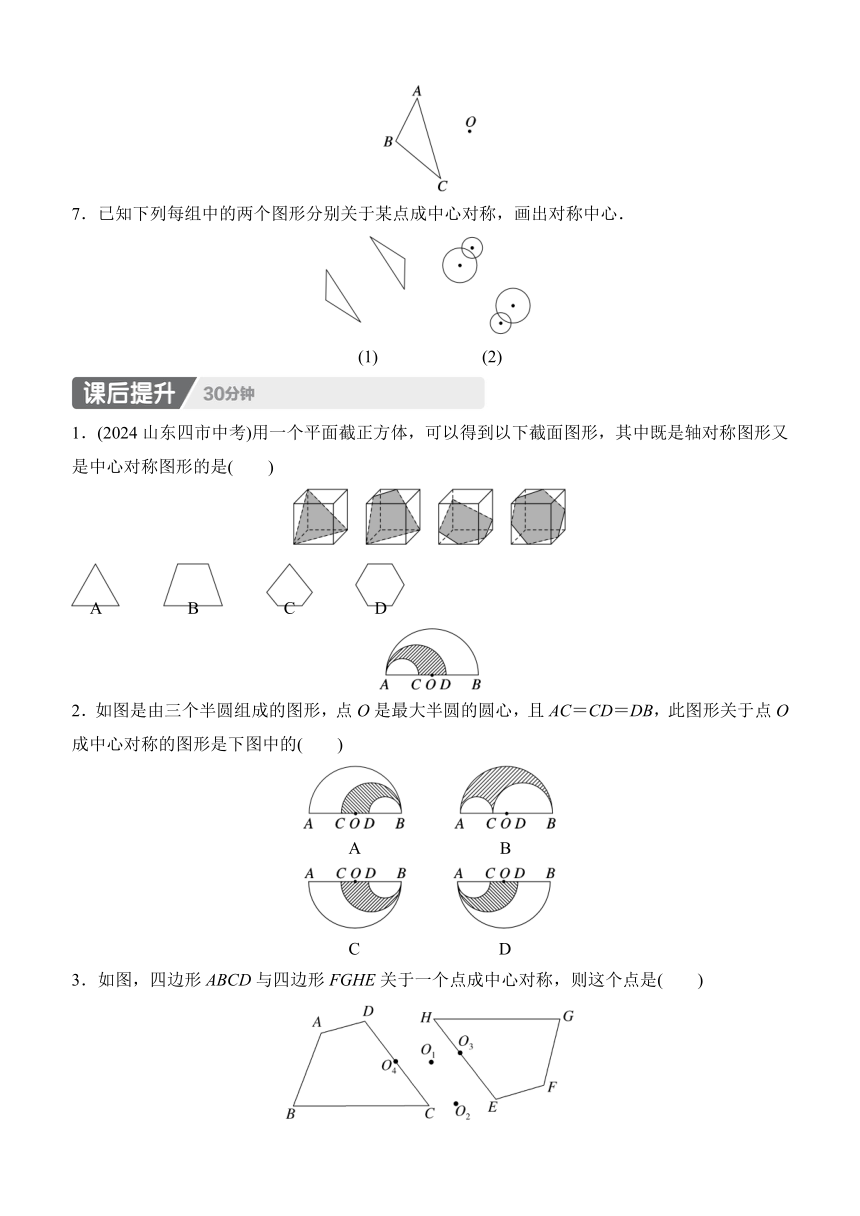
1.(2024内江中考)2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是( )
2.(2024泰安中考)下面图形中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
3.(2024潍坊中考)下列著名曲线中,既是轴对称图形也是中心对称图形的是( )
4.如图,△ABC与△DEF关于点O成中心对称,则AB=DE,BC∥________,AC=________.
5.如图为某公园中心对称的观赏鱼池,阴影部分为观赏喂鱼台,已知OA=OB=2 m.则阴影部分的面积为________m2.
6.如图,已知△ABC和点O.在图中画出△A′B′C′,使△A′B′C′与△ABC关于点O成中心对称.
7.已知下列每组中的两个图形分别关于某点成中心对称,画出对称中心.
(1) (2)
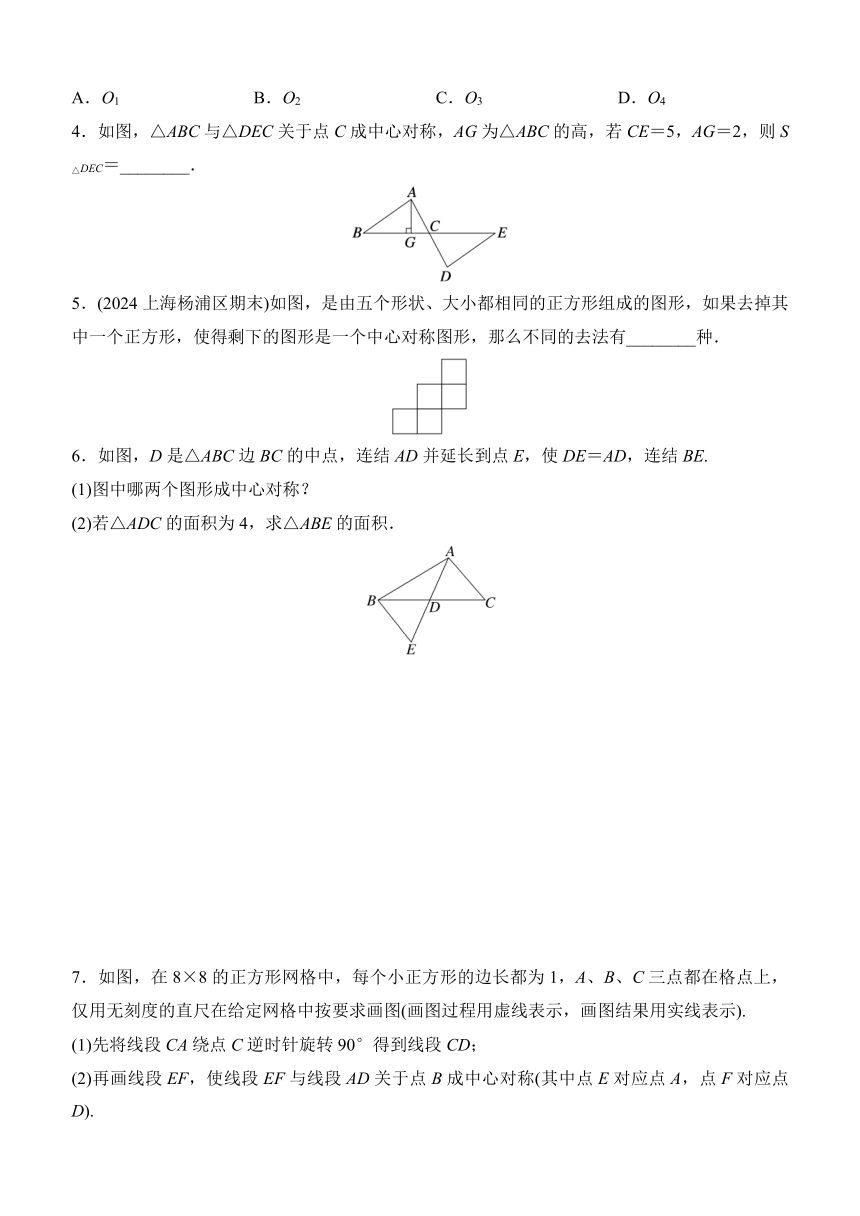
1.(2024山东四市中考)用一个平面截正方体,可以得到以下截面图形,其中既是轴对称图形又是中心对称图形的是( )
2.如图是由三个半圆组成的图形,点O是最大半圆的圆心,且AC=CD=DB,此图形关于点O成中心对称的图形是下图中的( )
A B
C D
3.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
4.如图,△ABC与△DEC关于点C成中心对称,AG为△ABC的高,若CE=5,AG=2,则S△DEC=________.
5.(2024上海杨浦区期末)如图,是由五个形状、大小都相同的正方形组成的图形,如果去掉其中一个正方形,使得剩下的图形是一个中心对称图形,那么不同的去法有________种.
6.如图,D是△ABC边BC的中点,连结AD并延长到点E,使DE=AD,连结BE.
(1)图中哪两个图形成中心对称?
(2)若△ADC的面积为4,求△ABE的面积.
7.如图,在8×8的正方形网格中,每个小正方形的边长都为1,A、B、C三点都在格点上,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线表示,画图结果用实线表示).
(1)先将线段CA绕点C逆时针旋转90°得到线段CD;
(2)再画线段EF,使线段EF与线段AD关于点B成中心对称(其中点E对应点A,点F对应点D).
8.(几何直观)如图,将边长为2的正方形剪成四个完全相同的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形.(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上)
【详解答案】
课堂达标
1.D 2.C 3.C
4.EF DF 5.8π
6.解:连结AO、BO、CO,并分别延长到点A′、B′、C′,使OA′=OA,OB′=OB,OC′=OC,连结A′B′、B′C′、A′C′,即得△A′B′C′,如图所示.
7.解:如图所示,点O、W分别为(1)(2)两组中的两个图形的对称中心.
(1) (2)
课后提升
1.D 解析:A.该图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
B.该图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
C.该图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
D.该图形既是轴对称图形,又是中心对称图形,故此选项符合题意.故选D.
2.C 解析:以最小半圆为例,绕点O旋转180°后,原图形在AB的左上方,那么新图形应在AB右下方.故选C.
3.A 解析:如图,连结HC和DE交于点O1.故选A.
4.5 解析:∵△ABC与△DEC关于点C成中心对称,
∴CE=BC,S△DEC=S△ABC.
∴S△ABC=BC×AG=×5×2=5.∴S△DEC=5.
5.2 解析:去掉一个正方形,得到中心对称图形,如图所示.
共2种方法.
6.解:(1)题图中△ADC和△EDB成中心对称.
(2)∵△ADC和△EDB成中心对称,△ADC的面积为4,∴△EDB的面积也为4.
∵D为BC的中点,
∴△ABD的面积也为4.
∴△ABE的面积为8.
7.解:(1)如图,CD即为所求.
(2)如图,EF即为所求.
8.解:①要求是轴对称图形但不是中心对称图形,则可作等腰梯形,如图1,四边形ABCD即为所求;
②要求是中心对称图形但不是轴对称图形,则可作一般平行四边形,如图2,四边形ABCD即为所求;
③要求既是轴对称图形又是中心对称图形,则可作菱形,如图3,四边形ABCD即为所求;
④要求既不是轴对称图形又不是中心对称图形,则可作一般四边形,如图4,四边形ABCD即为所求.
(答案不唯一)
图1
图2
图3
图4
1.(2024内江中考)2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是( )
2.(2024泰安中考)下面图形中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
3.(2024潍坊中考)下列著名曲线中,既是轴对称图形也是中心对称图形的是( )
4.如图,△ABC与△DEF关于点O成中心对称,则AB=DE,BC∥________,AC=________.
5.如图为某公园中心对称的观赏鱼池,阴影部分为观赏喂鱼台,已知OA=OB=2 m.则阴影部分的面积为________m2.
6.如图,已知△ABC和点O.在图中画出△A′B′C′,使△A′B′C′与△ABC关于点O成中心对称.
7.已知下列每组中的两个图形分别关于某点成中心对称,画出对称中心.
(1) (2)
1.(2024山东四市中考)用一个平面截正方体,可以得到以下截面图形,其中既是轴对称图形又是中心对称图形的是( )
2.如图是由三个半圆组成的图形,点O是最大半圆的圆心,且AC=CD=DB,此图形关于点O成中心对称的图形是下图中的( )
A B
C D
3.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
4.如图,△ABC与△DEC关于点C成中心对称,AG为△ABC的高,若CE=5,AG=2,则S△DEC=________.
5.(2024上海杨浦区期末)如图,是由五个形状、大小都相同的正方形组成的图形,如果去掉其中一个正方形,使得剩下的图形是一个中心对称图形,那么不同的去法有________种.
6.如图,D是△ABC边BC的中点,连结AD并延长到点E,使DE=AD,连结BE.
(1)图中哪两个图形成中心对称?
(2)若△ADC的面积为4,求△ABE的面积.
7.如图,在8×8的正方形网格中,每个小正方形的边长都为1,A、B、C三点都在格点上,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线表示,画图结果用实线表示).
(1)先将线段CA绕点C逆时针旋转90°得到线段CD;
(2)再画线段EF,使线段EF与线段AD关于点B成中心对称(其中点E对应点A,点F对应点D).
8.(几何直观)如图,将边长为2的正方形剪成四个完全相同的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形.(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上)
【详解答案】
课堂达标
1.D 2.C 3.C
4.EF DF 5.8π
6.解:连结AO、BO、CO,并分别延长到点A′、B′、C′,使OA′=OA,OB′=OB,OC′=OC,连结A′B′、B′C′、A′C′,即得△A′B′C′,如图所示.
7.解:如图所示,点O、W分别为(1)(2)两组中的两个图形的对称中心.
(1) (2)
课后提升
1.D 解析:A.该图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
B.该图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
C.该图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
D.该图形既是轴对称图形,又是中心对称图形,故此选项符合题意.故选D.
2.C 解析:以最小半圆为例,绕点O旋转180°后,原图形在AB的左上方,那么新图形应在AB右下方.故选C.
3.A 解析:如图,连结HC和DE交于点O1.故选A.
4.5 解析:∵△ABC与△DEC关于点C成中心对称,
∴CE=BC,S△DEC=S△ABC.
∴S△ABC=BC×AG=×5×2=5.∴S△DEC=5.
5.2 解析:去掉一个正方形,得到中心对称图形,如图所示.
共2种方法.
6.解:(1)题图中△ADC和△EDB成中心对称.
(2)∵△ADC和△EDB成中心对称,△ADC的面积为4,∴△EDB的面积也为4.
∵D为BC的中点,
∴△ABD的面积也为4.
∴△ABE的面积为8.
7.解:(1)如图,CD即为所求.
(2)如图,EF即为所求.
8.解:①要求是轴对称图形但不是中心对称图形,则可作等腰梯形,如图1,四边形ABCD即为所求;
②要求是中心对称图形但不是轴对称图形,则可作一般平行四边形,如图2,四边形ABCD即为所求;
③要求既是轴对称图形又是中心对称图形,则可作菱形,如图3,四边形ABCD即为所求;
④要求既不是轴对称图形又不是中心对称图形,则可作一般四边形,如图4,四边形ABCD即为所求.
(答案不唯一)
图1
图2
图3
图4
