9.5 图形的全等 练习(含答案)2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.5 图形的全等 练习(含答案)2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 00:00:00 | ||
图片预览

文档简介
9.5 图形的全等
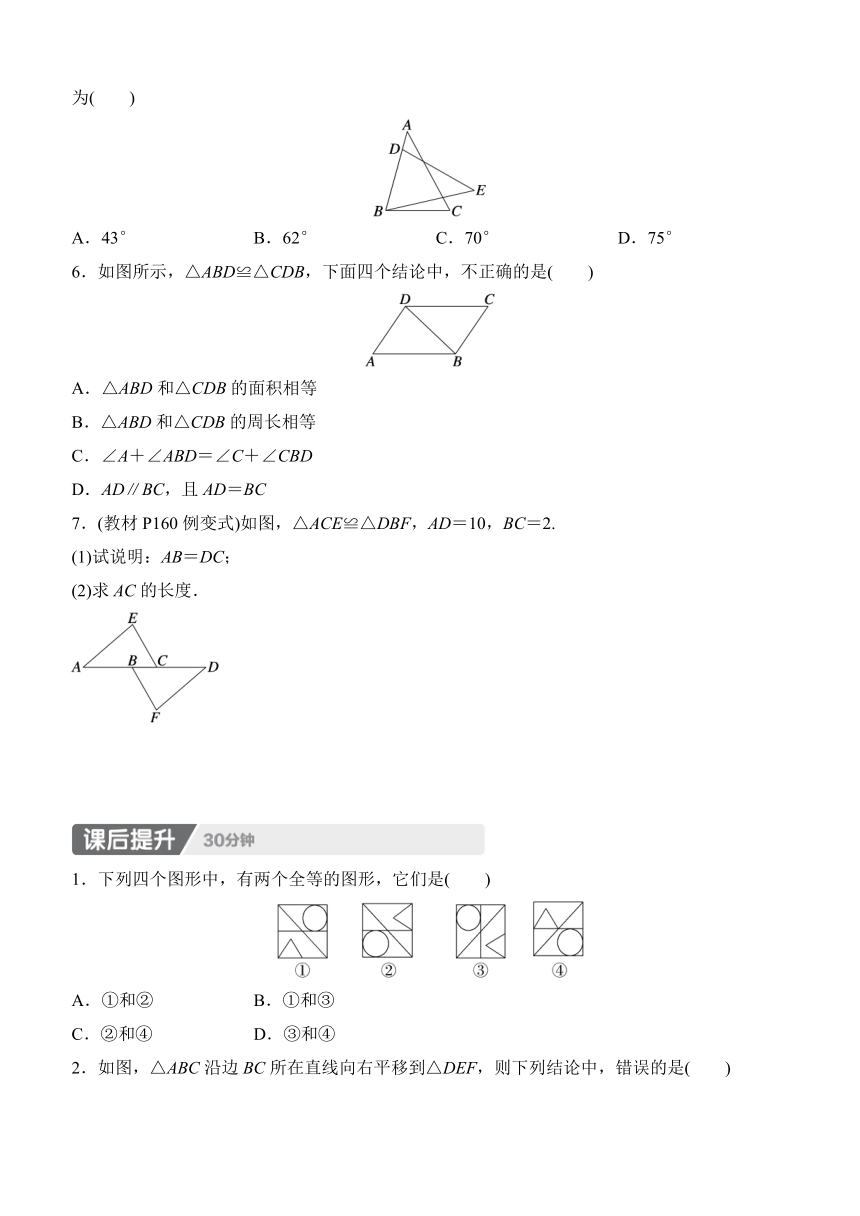
1.(2024苏州工业园区期末)下列各组图形中,属于全等图形的是( )
A. B.
C. D.
2.下列各组中的两个字母,是全等图形的一组是( )
A.A a B.B b C.C C D.D d
3.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是________.
4.如图所示的是两个全等的五边形,AB=7,AE=8,DE=11,HI=12,IJ=10,∠D=90°,∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的字母a、b、c、d、e、α、β所表示的值.
5.(2024防城港防城区月考)如图,△ABC≌△EDB,∠A=43°,∠C=62°,则∠BDE的度数为( )
A.43° B.62° C.70° D.75°
6.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,且AD=BC
7.(教材P160例变式)如图,△ACE≌△DBF,AD=10,BC=2.
(1)试说明:AB=DC;
(2)求AC的长度.
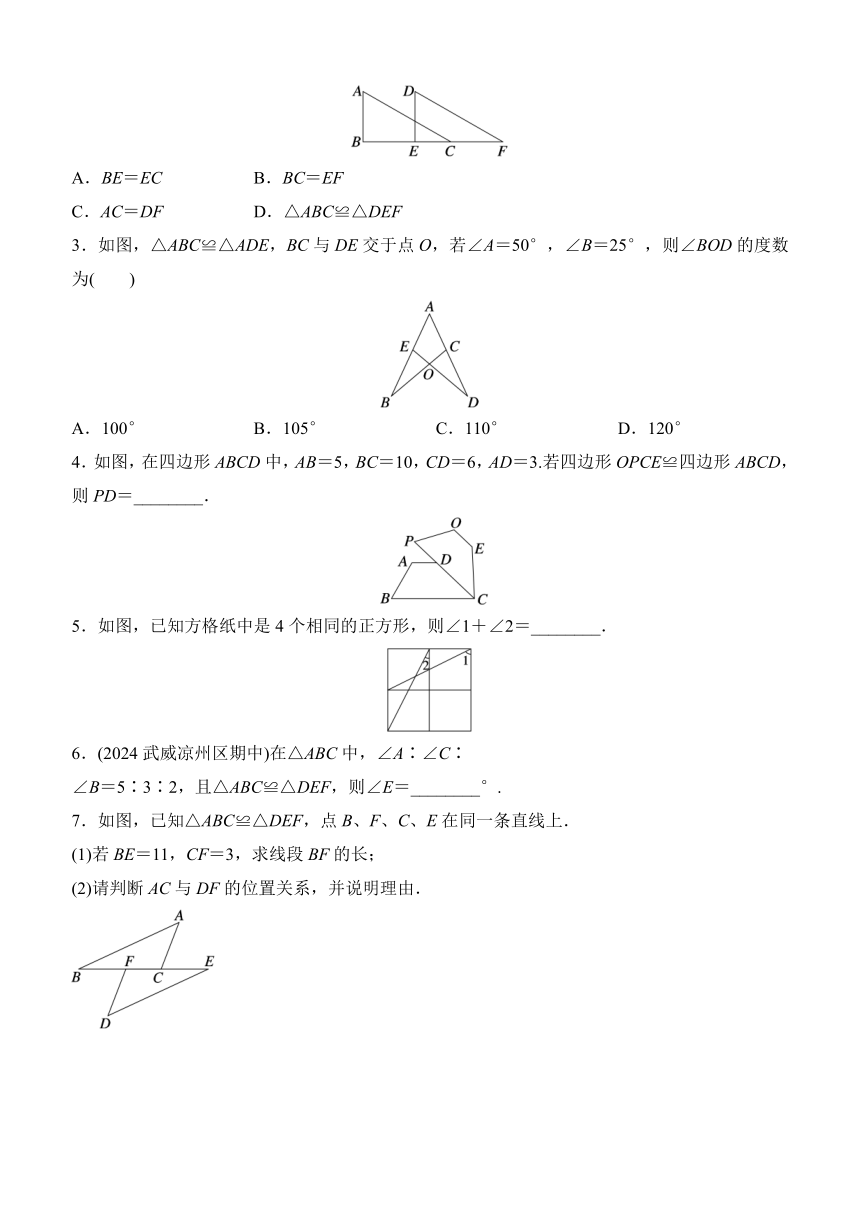
1.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.①和③
C.②和④ D.③和④
2.如图,△ABC沿边BC所在直线向右平移到△DEF,则下列结论中,错误的是( )
A.BE=EC B.BC=EF
C.AC=DF D.△ABC≌△DEF
3.如图,△ABC≌△ADE,BC与DE交于点O,若∠A=50°,∠B=25°,则∠BOD的度数为( )
A.100° B.105° C.110° D.120°
4.如图,在四边形ABCD中,AB=5,BC=10,CD=6,AD=3.若四边形OPCE≌四边形ABCD,则PD=________.
5.如图,已知方格纸中是4个相同的正方形,则∠1+∠2=________.
6.(2024武威凉州区期中)在△ABC中,∠A∶∠C∶
∠B=5∶3∶2,且△ABC≌△DEF,则∠E=________°.
7.如图,已知△ABC≌△DEF,点B、F、C、E在同一条直线上.
(1)若BE=11,CF=3,求线段BF的长;
(2)请判断AC与DF的位置关系,并说明理由.
8.如图所示,在正方形方格纸中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上,请你在图中找出一点D,再连结DE、DF,使以D、E、F为顶点的三角形与△ABC全等,这样的三角形可以画多少个?
9.(推理能力)如图,△ADF≌△CBE,∠FAB=∠ECD,且点E、B、D、F在一条直线上,判断AB与CD的位置关系,并加以说明.
【详解答案】
课堂达标
1.C 2.C 3.95°
4.解:对应顶点:A和G,E和F,C和I;
对应边:AB和GH,AE和GF,ED和FJ,CD和IJ,BC和HI;
对应角:∠A和∠G,∠B和∠H,∠C和∠I,∠D和∠J,∠E和∠F.
∵两个五边形全等,
∴a=12,b=10,c=7,d=8,e=11,α=90°,β=115°.
5.D 6.C
7.解:(1)∵△ACE≌△DBF,
∴AC=DB.
∴AC-BC=DB-BC,
即AB=DC.
(2)∵AD=10,BC=2,
∴AB=DC=×(10-2)=4.
∴AC=10-4=6.
课后提升
1.B 解析:全等的两个图形是①和③.故选B.
2.A 解析:∵△ABC沿边BC所在直线向右平移到△DEF,∴△ABC≌△DEF.∴BC=EF,AC=DF.
∴只有选项A是错误的.故选A.
3.A
4.4 解析:∵四边形OPCE≌四边形ABCD,BC=10,∴BC=PC=10.∵CD=6,∴PD=PC-CD=10-6=4.
5.90° 6.36
7.解:(1)∵△ABC≌△DEF,
∴BC=EF.
∴BF=CE.
∵BE=11,CF=3,
∴BF+CE=BE-CF=11-3=8.
∴BF=4.
(2)AC∥DF.理由如下:
∵△ABC≌△DEF,
∴∠ACB=∠DFE.
∴AC∥DF.
8.解:这样的三角形可以画4个.如图,D的位置有四处,分别是图中的D1、D2、D3、D4.这里画出D在D1处的图形.
9.解:AB与CD的位置关系是AB∥CD.理由如下:
如图,∵△ADF≌△CBE,
∴∠1=∠2,∠F=∠E,
又∵∠FAB=∠ECD.
∴∠FAB-∠1=∠ECD-∠2,
即∠BAD=∠BCD.
又∵点E、B、D、F在一条直线上,
∴∠3=∠1+∠F,∠4=∠2+∠E.
∴∠3=∠4.∴AD∥BC.
∴∠BAD+∠ABC=180°.
∴∠BCD+∠ABC=180°.
∴AB∥CD.
1.(2024苏州工业园区期末)下列各组图形中,属于全等图形的是( )
A. B.
C. D.
2.下列各组中的两个字母,是全等图形的一组是( )
A.A a B.B b C.C C D.D d
3.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是________.
4.如图所示的是两个全等的五边形,AB=7,AE=8,DE=11,HI=12,IJ=10,∠D=90°,∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的字母a、b、c、d、e、α、β所表示的值.
5.(2024防城港防城区月考)如图,△ABC≌△EDB,∠A=43°,∠C=62°,则∠BDE的度数为( )
A.43° B.62° C.70° D.75°
6.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,且AD=BC
7.(教材P160例变式)如图,△ACE≌△DBF,AD=10,BC=2.
(1)试说明:AB=DC;
(2)求AC的长度.
1.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.①和③
C.②和④ D.③和④
2.如图,△ABC沿边BC所在直线向右平移到△DEF,则下列结论中,错误的是( )
A.BE=EC B.BC=EF
C.AC=DF D.△ABC≌△DEF
3.如图,△ABC≌△ADE,BC与DE交于点O,若∠A=50°,∠B=25°,则∠BOD的度数为( )
A.100° B.105° C.110° D.120°
4.如图,在四边形ABCD中,AB=5,BC=10,CD=6,AD=3.若四边形OPCE≌四边形ABCD,则PD=________.
5.如图,已知方格纸中是4个相同的正方形,则∠1+∠2=________.
6.(2024武威凉州区期中)在△ABC中,∠A∶∠C∶
∠B=5∶3∶2,且△ABC≌△DEF,则∠E=________°.
7.如图,已知△ABC≌△DEF,点B、F、C、E在同一条直线上.
(1)若BE=11,CF=3,求线段BF的长;
(2)请判断AC与DF的位置关系,并说明理由.
8.如图所示,在正方形方格纸中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上,请你在图中找出一点D,再连结DE、DF,使以D、E、F为顶点的三角形与△ABC全等,这样的三角形可以画多少个?
9.(推理能力)如图,△ADF≌△CBE,∠FAB=∠ECD,且点E、B、D、F在一条直线上,判断AB与CD的位置关系,并加以说明.
【详解答案】
课堂达标
1.C 2.C 3.95°
4.解:对应顶点:A和G,E和F,C和I;
对应边:AB和GH,AE和GF,ED和FJ,CD和IJ,BC和HI;
对应角:∠A和∠G,∠B和∠H,∠C和∠I,∠D和∠J,∠E和∠F.
∵两个五边形全等,
∴a=12,b=10,c=7,d=8,e=11,α=90°,β=115°.
5.D 6.C
7.解:(1)∵△ACE≌△DBF,
∴AC=DB.
∴AC-BC=DB-BC,
即AB=DC.
(2)∵AD=10,BC=2,
∴AB=DC=×(10-2)=4.
∴AC=10-4=6.
课后提升
1.B 解析:全等的两个图形是①和③.故选B.
2.A 解析:∵△ABC沿边BC所在直线向右平移到△DEF,∴△ABC≌△DEF.∴BC=EF,AC=DF.
∴只有选项A是错误的.故选A.
3.A
4.4 解析:∵四边形OPCE≌四边形ABCD,BC=10,∴BC=PC=10.∵CD=6,∴PD=PC-CD=10-6=4.
5.90° 6.36
7.解:(1)∵△ABC≌△DEF,
∴BC=EF.
∴BF=CE.
∵BE=11,CF=3,
∴BF+CE=BE-CF=11-3=8.
∴BF=4.
(2)AC∥DF.理由如下:
∵△ABC≌△DEF,
∴∠ACB=∠DFE.
∴AC∥DF.
8.解:这样的三角形可以画4个.如图,D的位置有四处,分别是图中的D1、D2、D3、D4.这里画出D在D1处的图形.
9.解:AB与CD的位置关系是AB∥CD.理由如下:
如图,∵△ADF≌△CBE,
∴∠1=∠2,∠F=∠E,
又∵∠FAB=∠ECD.
∴∠FAB-∠1=∠ECD-∠2,
即∠BAD=∠BCD.
又∵点E、B、D、F在一条直线上,
∴∠3=∠1+∠F,∠4=∠2+∠E.
∴∠3=∠4.∴AD∥BC.
∴∠BAD+∠ABC=180°.
∴∠BCD+∠ABC=180°.
∴AB∥CD.
