第9章 轴对称、平移与旋转 评估测试卷(含详解) 2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 第9章 轴对称、平移与旋转 评估测试卷(含详解) 2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 00:00:00 | ||
图片预览

文档简介
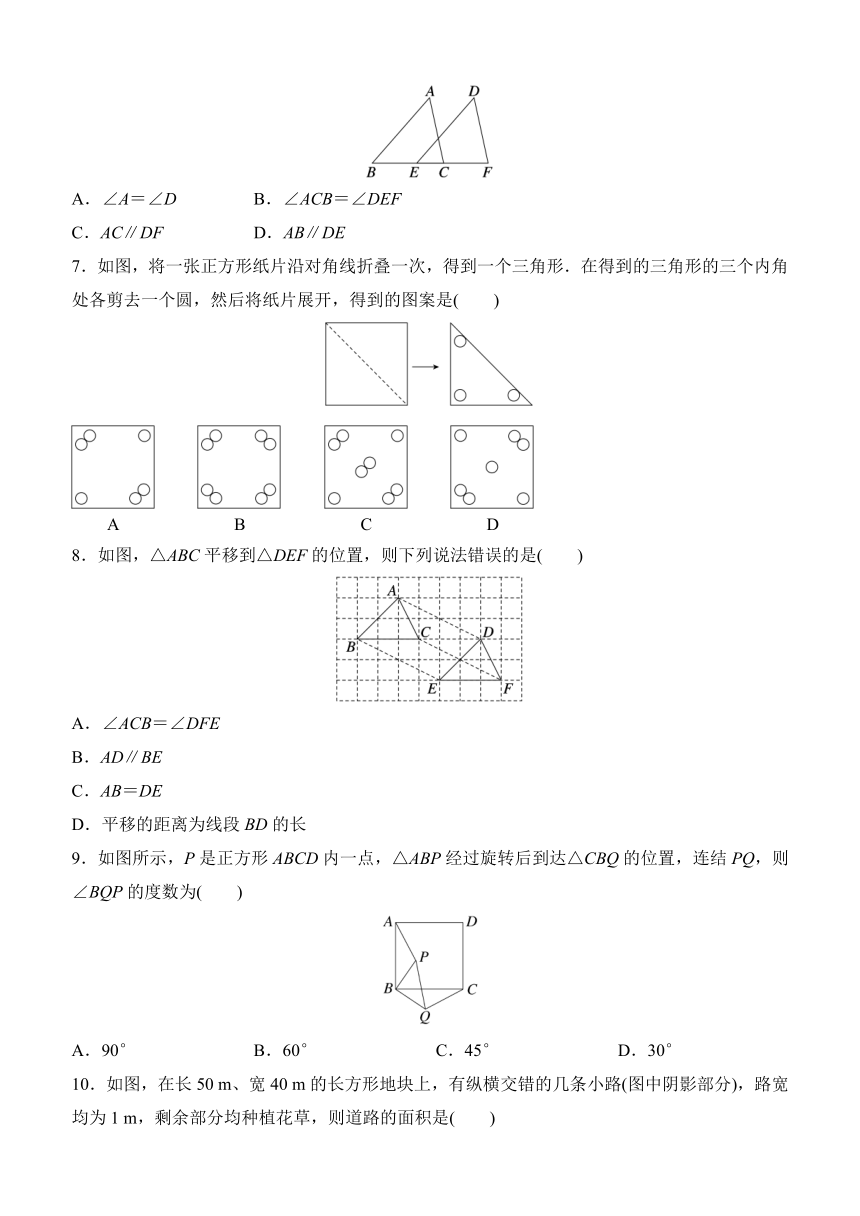
第9章轴对称 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列运动形式属于旋转的是( )
A.荡秋千 B.飞驰的火车
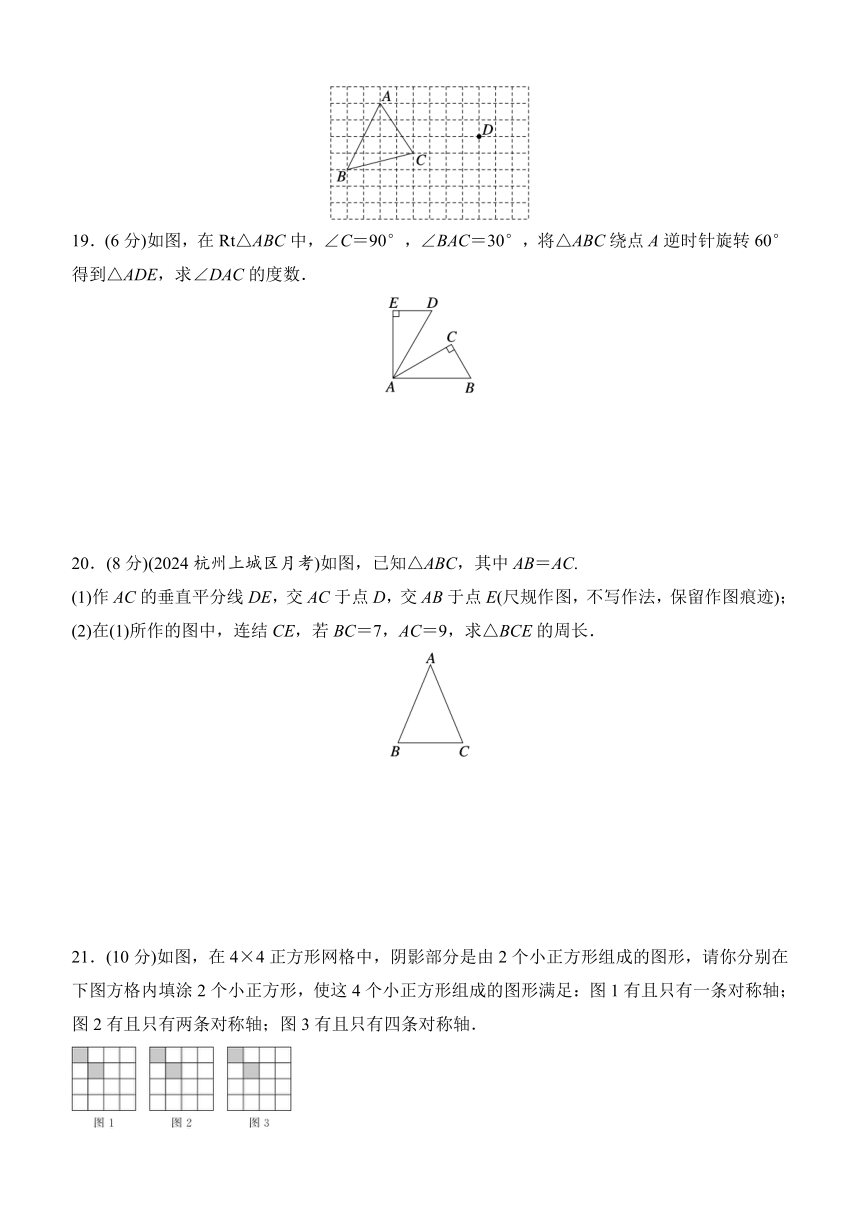
C.传送带移动 D.运动员掷出的标枪
2.(2024北京中考)下列图形中,既是轴对称图形又是中心对称图形的是( )
3.如图,将△ABC沿BC方向平移到△DEF,若A、D之间的距离为2,CE=3,则BF等于( )
A.6 B.7 C.8 D.9
4.如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A.α B.α-45°
C.45°-α D.90°-α
5.小强站在镜子前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是( )
A.15:01 B.10:51
C.10:21 D.12:01
6.如图,若△ABC≌△DEF,且点B、E、C、F在同一直线上,则下列结论错误的是( )
A.∠A=∠D B.∠ACB=∠DEF
C.AC∥DF D.AB∥DE
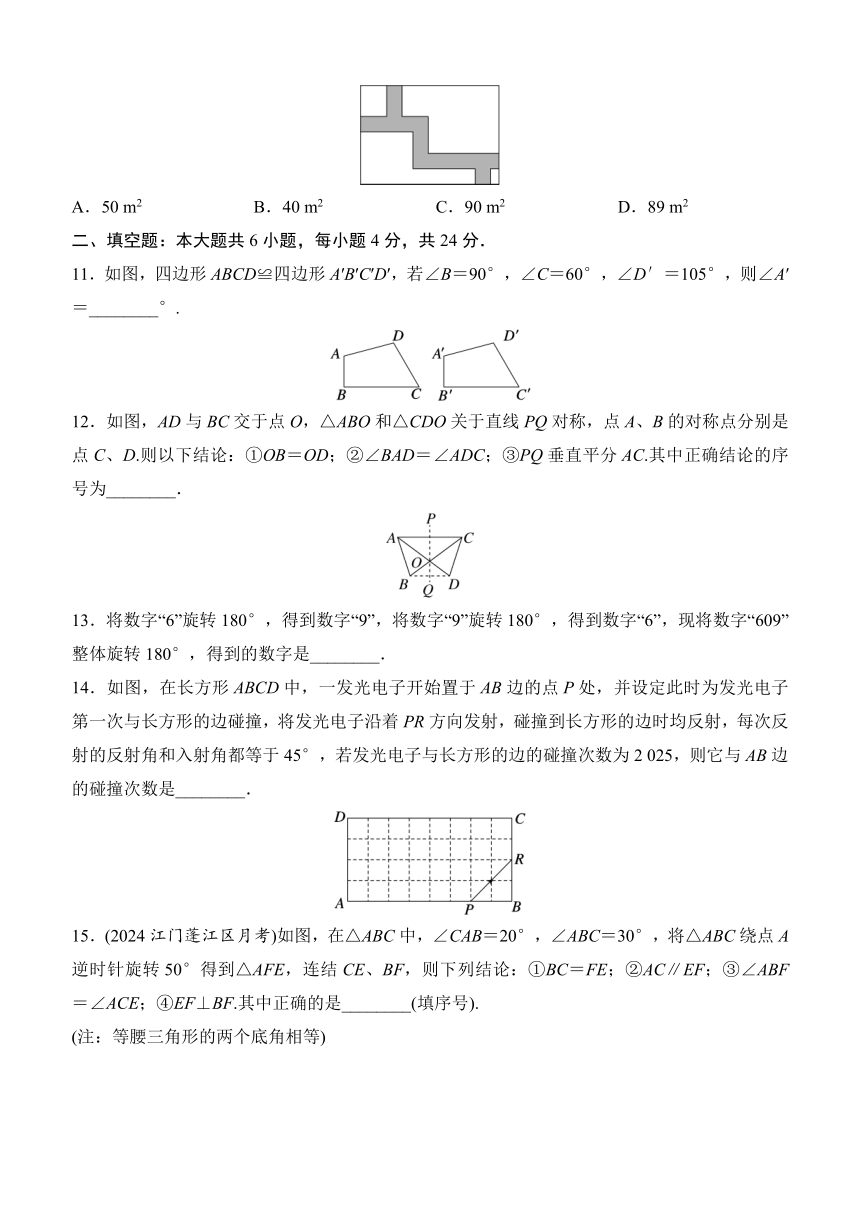
7.如图,将一张正方形纸片沿对角线折叠一次,得到一个三角形.在得到的三角形的三个内角处各剪去一个圆,然后将纸片展开,得到的图案是( )
8.如图,△ABC平移到△DEF的位置,则下列说法错误的是( )
A.∠ACB=∠DFE
B.AD∥BE
C.AB=DE
D.平移的距离为线段BD的长
9.如图所示,P是正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置,连结PQ,则∠BQP的度数为( )
A.90° B.60° C.45° D.30°
10.如图,在长50 m、宽40 m的长方形地块上,有纵横交错的几条小路(图中阴影部分),路宽均为1 m,剩余部分均种植花草,则道路的面积是( )
A.50 m2 B.40 m2 C.90 m2 D.89 m2
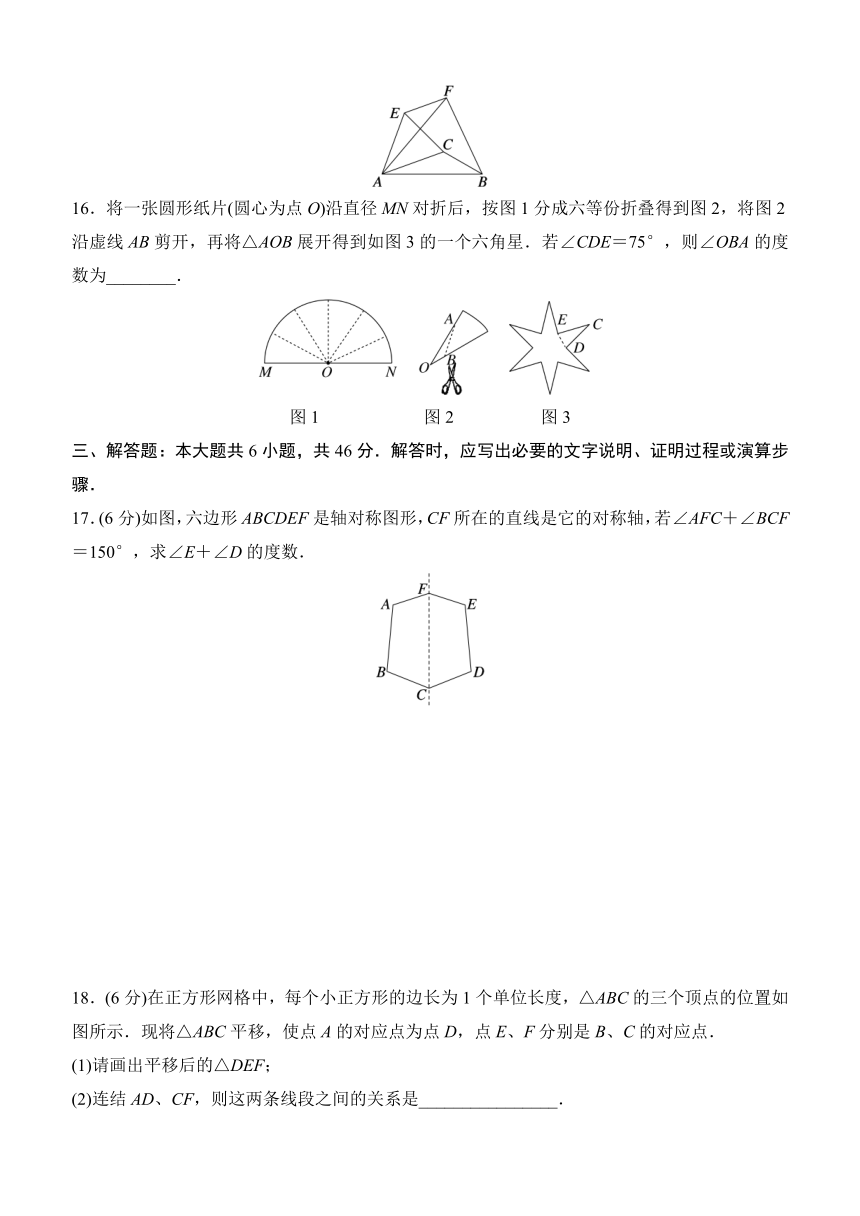
二、填空题:本大题共6小题,每小题4分,共24分.
11.如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=60°,∠D′=105°,则∠A′=________°.
12.如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A、B的对称点分别是点C、D.则以下结论:①OB=OD;②∠BAD=∠ADC;③PQ垂直平分AC.其中正确结论的序号为________.
13.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“609”整体旋转180°,得到的数字是________.
14.如图,在长方形ABCD中,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与长方形的边碰撞,将发光电子沿着PR方向发射,碰撞到长方形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与长方形的边的碰撞次数为2 025,则它与AB边的碰撞次数是________.
15.(2024江门蓬江区月考)如图,在△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕点A逆时针旋转50°得到△AFE,连结CE、BF,则下列结论:①BC=FE;②AC∥EF;③∠ABF=∠ACE;④EF⊥BF.其中正确的是________(填序号).
(注:等腰三角形的两个底角相等)
16.将一张圆形纸片(圆心为点O)沿直径MN对折后,按图1分成六等份折叠得到图2,将图2沿虚线AB剪开,再将△AOB展开得到如图3的一个六角星.若∠CDE=75°,则∠OBA的度数为________.
图1 图2 图3
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,求∠E+∠D的度数.
18.(6分)在正方形网格中,每个小正方形的边长为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A的对应点为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF;
(2)连结AD、CF,则这两条线段之间的关系是________________.
19.(6分)如图,在Rt△ABC中,∠C=90°,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△ADE,求∠DAC的度数.
20.(8分)(2024杭州上城区月考)如图,已知△ABC,其中AB=AC.
(1)作AC的垂直平分线DE,交AC于点D,交AB于点E(尺规作图,不写作法,保留作图痕迹);
(2)在(1)所作的图中,连结CE,若BC=7,AC=9,求△BCE的周长.
21.(10分)如图,在4×4正方形网格中,阴影部分是由2个小正方形组成的图形,请你分别在下图方格内填涂2个小正方形,使这4个小正方形组成的图形满足:图1有且只有一条对称轴;图2有且只有两条对称轴;图3有且只有四条对称轴.
22.(10分)如图,△ABC≌△ADC,∠B+∠D=200°,∠BAD=64°.
(1)求∠BCA的度数.
(2)若AB=6,CD=4,求四边形ABCD的周长.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2 cm得到△DEF.若CH=2 cm,EF=4 cm,则阴影部分的面积为多少平方厘米?
24.(10分)如图,将△ABC沿射线BC方向平移得到△DEF,A、B、C的对应点分别是D、E、F.
(1)若∠DAC=62°,求∠F的度数;
(2)若BC=9 cm,当AD=2EC时,求EC的长.
25.(10分)如图,已知在△ABC中,∠B=∠C,AB=AC=10 cm,BC=8 cm,点D为AB的中点,点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动,当△BPD与△CQP全等时,求点P运动的时间.
26.(10分)(2024盐城盐都区月考)综合与实践
【提出问题】唐朝诗人李颀的诗《古从军行》开头两句“白日登山望烽火,黄昏饮马傍交河”中隐含着一个有趣的数学问题——将军饮马.如图1,将军从山脚下的点A出发,到达河岸点P饮马后再回到点B宿营,他时常想,怎么走,才能使他每天走的路程之和最短呢?
【分析问题】
小亮:作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是饮马的地方,此时所走的路程就是最短的(如图2).
小慧:你能详细解释为什么吗?
图1
图2
图3
图4
小亮:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,我只要证明AC+CB<AC′+C′B.
∵直线l是点B、B′的对称轴,点C、C′在l上,
∴CB=CB′,C′B=C′B′……
请完整地写出小亮的证明过程.
【解决问题】
如图4,将军牵马从军营P处出发,到河流OA饮马,再到草地OB吃草,最后回到P处,试分别在边OA和OB上各找一点E、F,使得走过的路程最短(保留画图痕迹,辅助线用虚线,最短路径用实线).
27.(12分)如图,直线m、n相交于点P,且所成的锐角为45°,画出△ABC关于直线m的对称图形△A′B′C′,然后画出△A′B′C′关于直线n的对称图形△A″B″C″,你能发现△ABC与△A″B″C″有什么关系吗?若是平移,指出平移的方向和距离;若是旋转,指出旋转中心和旋转角度.
【详解答案】
1.A 解析:根据题意可知,A.荡秋千属于旋转,符合题意;B.飞驰的火车属于平移,不符合题意;C.传送带移动属于平移,不符合题意;D.运动员掷出的标枪形成的路线是曲线,不符合题意.故选A.
2.B 解析:A.图形是中心对称图形,不是轴对称图形,不符合题意;B.图形是中心对称图形,也是轴对称图形,符合题意;C.图形不是中心对称图形,也不是轴对称图形,不符合题意;D.图形不是中心对称图形,是轴对称图形,不符合题意.故选B.
3.B 解析:∵将△ABC沿BC方向平移到△DEF的位置,点A、D之间的距离为2,∴BE=CF=2.
∵CE=3,∴BF=CF+BE+CE=2+2+3=7.故选B.
4.C 解析:由旋转的性质可得∠CA′B′=∠CAB=α,∠ACA′=90°,AC=A′C,∴△ACA′为等腰直角三角形.∴∠AA′C=45°.
∴∠AA′B′=45°-α.故选C.
5.C 解析:电子表的实际时刻是10:21.故选C.
6.B 解析:∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∠ABC=∠DEF.∴AC∥DF,AB∥DE.故选B.
7.A 解析:在对折后的三角形的三个内角处各剪去一个圆,展开后会得到6个圆,所以只有选项A符合题意.故选A.
8.D 解析:由平移的性质可知,∠ACB=∠DFE,故选项A不符合题意;由平移的性质可知,AD∥BE,故选项B不符合题意;由平移的性质可知,AB=DE,故选项C不符合题意;由平移的性质可知,平移距离为线段BE的长,故选项D符合题意.故选D.
9.C 解析:由旋转可得,∠ABP=∠CBQ,PB=BQ.∴∠PBQ=∠ABC=90°.∴△PBQ是等腰直角三角形.∴∠BQP=45°.故选C.
10.D 解析:长50 m、宽40 m的长方形地块的面积为50×40=2 000(m2),种植花草的面积为(50-1)×(40-1)=1 911(m2),故道路的面积为2 000-1 911=89(m2).故选D.
11.105 解析:∵四边形ABCD≌四边形A′B′C′D′,
∴∠A=∠A′,∠D=∠D′.
∵∠D′=105°,∴∠D=105°.
∵∠B=90°,∠C=60°,
∴∠A=105°.∴∠A′=105°.
12.①③ 解析:∵△ABO和△CDO关于直线PQ对称,∴OB=OD,故①正确;∴∠BAD=∠DCB,
∠ABC=∠ADC,
∴∠BAD≠∠ADC,故②错误;
∵点A和点C关于PQ对称,∴PQ垂直平分AC,故③正确.综上所述,正确结论的序号为①③.
13.609 解析:将数字“609”整体旋转180°,得到的数字是609.
14.675 解析:如图,
每6次碰撞为一个循环组依次循环,经过6次碰撞后电子回到出发点,且每次循环它与AB边碰撞2次,∵2 025÷6=337……3,
∴它与AB边的碰撞次数是337×2+1=675.
15.①②③ 解析:由题意知,△ABC绕点A逆时针旋转50°得到△AFE,
∴△ABC≌△AFE,∠EAC=∠FAB=50°.
∵∠CAB=20°,∠ABC=30°,
∴∠CAB=∠EAF=20°,∠ABC=
∠AFE=30°,AB=AF,AC=AE,BC=FE.
故①符合题意.
∴∠ABF=∠AFB=(180°-∠FAB)=65°,∠ACE=∠AEC=(180°-∠EAC)=65°.
∴∠ABF=∠ACE.
故③符合题意.
∴∠FAC=∠FAB-∠BAC=30°.
∴∠FAC=∠EFA.
∴AC∥EF.
故②符合题意.
∴∠EFB=∠EFA+∠AFB=30°+65°=95°.
故④不符合题意.
16.135° 解析:由题知,∠AOB=×180°=30°,由翻折知∠OAB=∠DCE,∠CDE=∠CED.
∵∠CDE=75°,∴∠DCE=180°-75°-75°=30°.
∴∠OAB=∠DCE=×30°=15°.
∴∠OBA=180°-∠AOB-∠OAB=180°-30°-15°=135°.
17.解:∵六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,
∴∠A=∠E,∠B=∠D.
∵∠AFC+∠BCF=150°,
∴∠A+∠B=360°-150°=210°.
∴∠E+∠D=∠A+∠B=210°.
18.解:(1)如图.
(2)平行且相等
19.解:∵将△ABC绕点A逆时针旋转60°得到△ADE,
∴∠BAD=60°.
∵∠BAC=30°,
∴∠DAC=∠BAD-∠BAC=60°-30°=30°.
∴∠DAC的度数是30°.
20.解:(1)如图所示,直线DE即为所求.
(2)∵AB=AC=9,DE垂直平分AC,
∴DE是△ACE的对称轴.
∴AE=EC.
∴△BCE的周长=BC+BE+CE=BC+BE+AE=BC+AB=16.
21.解:如图所示.
22.解:(1)∵△ABC≌△ADC,
∴∠BAC=∠DAC,∠B=∠D.
∵∠BAD=64°,∠B+∠D=200°,
∴∠B=∠D=100°,∠BAC=∠DAC=32°.
∴∠BCA=180°-100°-32°=48°.
(2)∵△ABC≌△ADC,
∴AD=AB=6,BC=CD=4.
∴四边形ABCD的周长=AD+AB+BC+CD=6+6+4+4=20.
23.解:∵将△ABC沿AB方向平移2 cm得到△DEF,
∴BE=2 cm,BC=EF=4 cm,
S△ABC=S△DEF.
∴BH=BC-CH=2 cm.
∴阴影部分的面积=S△ABC-S△DBH=S△DEF-S△DBH=S梯形BHFE==6 cm2.
24.解:(1)因为△DEF由△ABC沿射线BC方向平移得到,
所以AD∥BF,AC∥DF.
所以∠ACB=∠DAC,∠F=∠ACB.
所以∠F=∠DAC=62°.
(2)由平移可知,AD=BE.
又因为AD=2EC,
所以BE=2EC,即BC=3EC.
因为BC=9 cm,
所以3EC=9 cm.
所以EC=3 cm.
25.解:∵点D为AB的中点,AB=10 cm,
∴BD=AD=5 cm.
设点P运动的时间是x s,
则BP=CQ=3x cm,CP=(8-3x)cm,
若BD与CQ是对应边,则BD=CQ,∴5=3x,
∴x=.
此时BP=3×=5(cm),CP=8-5=3(cm),BP≠CP,故舍去;
若BD与CP是对应边,则BD=CP,
∴5=8-3x.
∴x=1,符合题意.
综上,点P运动的时间是1 s.
26.解:【分析问题】根据题意可知,CB=CB′,C′B=C′B′,
∴AC+CB=AC+CB′=AB′,AC′+C′B=AC′+C′B′.
∵AB′<AC′+C′B′,
∴AC+CB<AC′+C′B.
∴作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是饮马的地方.
【解决问题】如图所示,分别作点P关于OA、OB的对称点C、D,连结CD分别交OA、OB于E、F,则点E、F即为所求,路线PE、EF、PF即为最短路径.
27.解:如图,△A′B′C′和△A″B″C″为所作.
∵△ABC和△A′B′C′关于直线m对称,
∴PA=PA′,PA与直线m的夹角等于PA′与直线m的夹角.
∵△A′B′C′和△A″B″C″关于直线n对称,
∴PA″=PA′,PA″与直线n的夹角等于PA′与直线n的夹角.
∴PA=PA″,∠APA″=2×45°=90°.
同理得到PB=PB″,∠BPB″=90°,PC=PC″,∠CPC″=90°.
∴△ABC绕点P逆时针旋转90°得到△A″B″C″.
旋转中心为点P,旋转角度为90°.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列运动形式属于旋转的是( )
A.荡秋千 B.飞驰的火车
C.传送带移动 D.运动员掷出的标枪
2.(2024北京中考)下列图形中,既是轴对称图形又是中心对称图形的是( )
3.如图,将△ABC沿BC方向平移到△DEF,若A、D之间的距离为2,CE=3,则BF等于( )
A.6 B.7 C.8 D.9
4.如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A.α B.α-45°
C.45°-α D.90°-α
5.小强站在镜子前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是( )
A.15:01 B.10:51
C.10:21 D.12:01
6.如图,若△ABC≌△DEF,且点B、E、C、F在同一直线上,则下列结论错误的是( )
A.∠A=∠D B.∠ACB=∠DEF
C.AC∥DF D.AB∥DE
7.如图,将一张正方形纸片沿对角线折叠一次,得到一个三角形.在得到的三角形的三个内角处各剪去一个圆,然后将纸片展开,得到的图案是( )
8.如图,△ABC平移到△DEF的位置,则下列说法错误的是( )
A.∠ACB=∠DFE
B.AD∥BE
C.AB=DE
D.平移的距离为线段BD的长
9.如图所示,P是正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置,连结PQ,则∠BQP的度数为( )
A.90° B.60° C.45° D.30°
10.如图,在长50 m、宽40 m的长方形地块上,有纵横交错的几条小路(图中阴影部分),路宽均为1 m,剩余部分均种植花草,则道路的面积是( )
A.50 m2 B.40 m2 C.90 m2 D.89 m2
二、填空题:本大题共6小题,每小题4分,共24分.
11.如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=60°,∠D′=105°,则∠A′=________°.
12.如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A、B的对称点分别是点C、D.则以下结论:①OB=OD;②∠BAD=∠ADC;③PQ垂直平分AC.其中正确结论的序号为________.
13.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“609”整体旋转180°,得到的数字是________.
14.如图,在长方形ABCD中,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与长方形的边碰撞,将发光电子沿着PR方向发射,碰撞到长方形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与长方形的边的碰撞次数为2 025,则它与AB边的碰撞次数是________.
15.(2024江门蓬江区月考)如图,在△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕点A逆时针旋转50°得到△AFE,连结CE、BF,则下列结论:①BC=FE;②AC∥EF;③∠ABF=∠ACE;④EF⊥BF.其中正确的是________(填序号).
(注:等腰三角形的两个底角相等)
16.将一张圆形纸片(圆心为点O)沿直径MN对折后,按图1分成六等份折叠得到图2,将图2沿虚线AB剪开,再将△AOB展开得到如图3的一个六角星.若∠CDE=75°,则∠OBA的度数为________.
图1 图2 图3
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,求∠E+∠D的度数.
18.(6分)在正方形网格中,每个小正方形的边长为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A的对应点为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF;
(2)连结AD、CF,则这两条线段之间的关系是________________.
19.(6分)如图,在Rt△ABC中,∠C=90°,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△ADE,求∠DAC的度数.
20.(8分)(2024杭州上城区月考)如图,已知△ABC,其中AB=AC.
(1)作AC的垂直平分线DE,交AC于点D,交AB于点E(尺规作图,不写作法,保留作图痕迹);
(2)在(1)所作的图中,连结CE,若BC=7,AC=9,求△BCE的周长.
21.(10分)如图,在4×4正方形网格中,阴影部分是由2个小正方形组成的图形,请你分别在下图方格内填涂2个小正方形,使这4个小正方形组成的图形满足:图1有且只有一条对称轴;图2有且只有两条对称轴;图3有且只有四条对称轴.
22.(10分)如图,△ABC≌△ADC,∠B+∠D=200°,∠BAD=64°.
(1)求∠BCA的度数.
(2)若AB=6,CD=4,求四边形ABCD的周长.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2 cm得到△DEF.若CH=2 cm,EF=4 cm,则阴影部分的面积为多少平方厘米?
24.(10分)如图,将△ABC沿射线BC方向平移得到△DEF,A、B、C的对应点分别是D、E、F.
(1)若∠DAC=62°,求∠F的度数;
(2)若BC=9 cm,当AD=2EC时,求EC的长.
25.(10分)如图,已知在△ABC中,∠B=∠C,AB=AC=10 cm,BC=8 cm,点D为AB的中点,点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动,当△BPD与△CQP全等时,求点P运动的时间.
26.(10分)(2024盐城盐都区月考)综合与实践
【提出问题】唐朝诗人李颀的诗《古从军行》开头两句“白日登山望烽火,黄昏饮马傍交河”中隐含着一个有趣的数学问题——将军饮马.如图1,将军从山脚下的点A出发,到达河岸点P饮马后再回到点B宿营,他时常想,怎么走,才能使他每天走的路程之和最短呢?
【分析问题】
小亮:作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是饮马的地方,此时所走的路程就是最短的(如图2).
小慧:你能详细解释为什么吗?
图1
图2
图3
图4
小亮:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,我只要证明AC+CB<AC′+C′B.
∵直线l是点B、B′的对称轴,点C、C′在l上,
∴CB=CB′,C′B=C′B′……
请完整地写出小亮的证明过程.
【解决问题】
如图4,将军牵马从军营P处出发,到河流OA饮马,再到草地OB吃草,最后回到P处,试分别在边OA和OB上各找一点E、F,使得走过的路程最短(保留画图痕迹,辅助线用虚线,最短路径用实线).
27.(12分)如图,直线m、n相交于点P,且所成的锐角为45°,画出△ABC关于直线m的对称图形△A′B′C′,然后画出△A′B′C′关于直线n的对称图形△A″B″C″,你能发现△ABC与△A″B″C″有什么关系吗?若是平移,指出平移的方向和距离;若是旋转,指出旋转中心和旋转角度.
【详解答案】
1.A 解析:根据题意可知,A.荡秋千属于旋转,符合题意;B.飞驰的火车属于平移,不符合题意;C.传送带移动属于平移,不符合题意;D.运动员掷出的标枪形成的路线是曲线,不符合题意.故选A.
2.B 解析:A.图形是中心对称图形,不是轴对称图形,不符合题意;B.图形是中心对称图形,也是轴对称图形,符合题意;C.图形不是中心对称图形,也不是轴对称图形,不符合题意;D.图形不是中心对称图形,是轴对称图形,不符合题意.故选B.
3.B 解析:∵将△ABC沿BC方向平移到△DEF的位置,点A、D之间的距离为2,∴BE=CF=2.
∵CE=3,∴BF=CF+BE+CE=2+2+3=7.故选B.
4.C 解析:由旋转的性质可得∠CA′B′=∠CAB=α,∠ACA′=90°,AC=A′C,∴△ACA′为等腰直角三角形.∴∠AA′C=45°.
∴∠AA′B′=45°-α.故选C.
5.C 解析:电子表的实际时刻是10:21.故选C.
6.B 解析:∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∠ABC=∠DEF.∴AC∥DF,AB∥DE.故选B.
7.A 解析:在对折后的三角形的三个内角处各剪去一个圆,展开后会得到6个圆,所以只有选项A符合题意.故选A.
8.D 解析:由平移的性质可知,∠ACB=∠DFE,故选项A不符合题意;由平移的性质可知,AD∥BE,故选项B不符合题意;由平移的性质可知,AB=DE,故选项C不符合题意;由平移的性质可知,平移距离为线段BE的长,故选项D符合题意.故选D.
9.C 解析:由旋转可得,∠ABP=∠CBQ,PB=BQ.∴∠PBQ=∠ABC=90°.∴△PBQ是等腰直角三角形.∴∠BQP=45°.故选C.
10.D 解析:长50 m、宽40 m的长方形地块的面积为50×40=2 000(m2),种植花草的面积为(50-1)×(40-1)=1 911(m2),故道路的面积为2 000-1 911=89(m2).故选D.
11.105 解析:∵四边形ABCD≌四边形A′B′C′D′,
∴∠A=∠A′,∠D=∠D′.
∵∠D′=105°,∴∠D=105°.
∵∠B=90°,∠C=60°,
∴∠A=105°.∴∠A′=105°.
12.①③ 解析:∵△ABO和△CDO关于直线PQ对称,∴OB=OD,故①正确;∴∠BAD=∠DCB,
∠ABC=∠ADC,
∴∠BAD≠∠ADC,故②错误;
∵点A和点C关于PQ对称,∴PQ垂直平分AC,故③正确.综上所述,正确结论的序号为①③.
13.609 解析:将数字“609”整体旋转180°,得到的数字是609.
14.675 解析:如图,
每6次碰撞为一个循环组依次循环,经过6次碰撞后电子回到出发点,且每次循环它与AB边碰撞2次,∵2 025÷6=337……3,
∴它与AB边的碰撞次数是337×2+1=675.
15.①②③ 解析:由题意知,△ABC绕点A逆时针旋转50°得到△AFE,
∴△ABC≌△AFE,∠EAC=∠FAB=50°.
∵∠CAB=20°,∠ABC=30°,
∴∠CAB=∠EAF=20°,∠ABC=
∠AFE=30°,AB=AF,AC=AE,BC=FE.
故①符合题意.
∴∠ABF=∠AFB=(180°-∠FAB)=65°,∠ACE=∠AEC=(180°-∠EAC)=65°.
∴∠ABF=∠ACE.
故③符合题意.
∴∠FAC=∠FAB-∠BAC=30°.
∴∠FAC=∠EFA.
∴AC∥EF.
故②符合题意.
∴∠EFB=∠EFA+∠AFB=30°+65°=95°.
故④不符合题意.
16.135° 解析:由题知,∠AOB=×180°=30°,由翻折知∠OAB=∠DCE,∠CDE=∠CED.
∵∠CDE=75°,∴∠DCE=180°-75°-75°=30°.
∴∠OAB=∠DCE=×30°=15°.
∴∠OBA=180°-∠AOB-∠OAB=180°-30°-15°=135°.
17.解:∵六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,
∴∠A=∠E,∠B=∠D.
∵∠AFC+∠BCF=150°,
∴∠A+∠B=360°-150°=210°.
∴∠E+∠D=∠A+∠B=210°.
18.解:(1)如图.
(2)平行且相等
19.解:∵将△ABC绕点A逆时针旋转60°得到△ADE,
∴∠BAD=60°.
∵∠BAC=30°,
∴∠DAC=∠BAD-∠BAC=60°-30°=30°.
∴∠DAC的度数是30°.
20.解:(1)如图所示,直线DE即为所求.
(2)∵AB=AC=9,DE垂直平分AC,
∴DE是△ACE的对称轴.
∴AE=EC.
∴△BCE的周长=BC+BE+CE=BC+BE+AE=BC+AB=16.
21.解:如图所示.
22.解:(1)∵△ABC≌△ADC,
∴∠BAC=∠DAC,∠B=∠D.
∵∠BAD=64°,∠B+∠D=200°,
∴∠B=∠D=100°,∠BAC=∠DAC=32°.
∴∠BCA=180°-100°-32°=48°.
(2)∵△ABC≌△ADC,
∴AD=AB=6,BC=CD=4.
∴四边形ABCD的周长=AD+AB+BC+CD=6+6+4+4=20.
23.解:∵将△ABC沿AB方向平移2 cm得到△DEF,
∴BE=2 cm,BC=EF=4 cm,
S△ABC=S△DEF.
∴BH=BC-CH=2 cm.
∴阴影部分的面积=S△ABC-S△DBH=S△DEF-S△DBH=S梯形BHFE==6 cm2.
24.解:(1)因为△DEF由△ABC沿射线BC方向平移得到,
所以AD∥BF,AC∥DF.
所以∠ACB=∠DAC,∠F=∠ACB.
所以∠F=∠DAC=62°.
(2)由平移可知,AD=BE.
又因为AD=2EC,
所以BE=2EC,即BC=3EC.
因为BC=9 cm,
所以3EC=9 cm.
所以EC=3 cm.
25.解:∵点D为AB的中点,AB=10 cm,
∴BD=AD=5 cm.
设点P运动的时间是x s,
则BP=CQ=3x cm,CP=(8-3x)cm,
若BD与CQ是对应边,则BD=CQ,∴5=3x,
∴x=.
此时BP=3×=5(cm),CP=8-5=3(cm),BP≠CP,故舍去;
若BD与CP是对应边,则BD=CP,
∴5=8-3x.
∴x=1,符合题意.
综上,点P运动的时间是1 s.
26.解:【分析问题】根据题意可知,CB=CB′,C′B=C′B′,
∴AC+CB=AC+CB′=AB′,AC′+C′B=AC′+C′B′.
∵AB′<AC′+C′B′,
∴AC+CB<AC′+C′B.
∴作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是饮马的地方.
【解决问题】如图所示,分别作点P关于OA、OB的对称点C、D,连结CD分别交OA、OB于E、F,则点E、F即为所求,路线PE、EF、PF即为最短路径.
27.解:如图,△A′B′C′和△A″B″C″为所作.
∵△ABC和△A′B′C′关于直线m对称,
∴PA=PA′,PA与直线m的夹角等于PA′与直线m的夹角.
∵△A′B′C′和△A″B″C″关于直线n对称,
∴PA″=PA′,PA″与直线n的夹角等于PA′与直线n的夹角.
∴PA=PA″,∠APA″=2×45°=90°.
同理得到PB=PB″,∠BPB″=90°,PC=PC″,∠CPC″=90°.
∴△ABC绕点P逆时针旋转90°得到△A″B″C″.
旋转中心为点P,旋转角度为90°.
