第8章三角形 评估测试卷(含答案) 2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 第8章三角形 评估测试卷(含答案) 2024-2025学年数学华东师大版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 21:00:02 | ||
图片预览

文档简介
第8章三角形 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.如图,BE是△ABC的高的是( )
A B
C D
2.(新情境)从数学角度看下列四幅图片有一个与众不同,该图片是( )
3.如图,∠DBA=105°,∠ECA=125°,则∠A的度数是( )
A.75° B.60° C.55° D.50°
4.一个多边形,它的内角和比外角和的4倍多180°,则这个多边形的边数是( )
A.9 B.10 C.11 D.12
5.(2024武威凉州区期中)已知三角形的两边长分别为2和5,则第三边长不可能是( )
A.4 B.5 C.6 D.7
6.将一副三角板按如图所示的方式摆放,DE经过点B,AC⊥DE,BC与DF交于点G,则∠BGF的度数为( )
A.15° B.135° C.165° D.155°
7.若一个正多边形的每一个外角都等于三角形内角和的,则这个正多边形为( )
A.六边形 B.八边形
C.十边形 D.十二边形
8.如图,在△ABC中,∠C=60°,把△ABC沿直线DE折叠,使得点B与点A重合.若AD恰好平分∠BAC,则∠BDE的度数为( )
A.30° B.40° C.50° D.60°
9.如图,大建从A点出发沿直线前进8 m到达点B后向左旋转的角度为α,再沿直线前进8 m,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72 m,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
10.如图,△ABC中,D、E、F分别是BC、AD、EC的中点,若S△ABD=4,则S△BFC=( )
A.2 B.1 C. D.
二、填空题:本大题共6小题,每小题4分,共24分.
11.如图,点D是△ABC的边CB延长线上一点,若∠ABD=100°,∠A=60°,则∠C=________.
12.(2024重庆B卷中考)若正多边形的一个外角是45°,则这个正多边形的边数为________.
13.如图,为估计池塘两岸A、B两点间的距离,小奇在池塘一侧选取了一点P.分别测得PA=7 m,PB=5 m,若A、B间的距离长度为偶数(单位:m),那么A、B间的最大距离是________m.
14.如图,在△ABC中,P是∠ABC和∠ACB的平分线的交点.若∠P=2∠A,则∠A=________°.
15.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为________.
16.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An,设∠A=θ,则∠A2 024=________.
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,已知五边形ABCDE中,AB∥CD,求x的值.
18.(6分)(2024淮安期末)如图,∠ABE是四边形ABCD的外角,已知∠ABE=∠D.
试说明:∠A+∠C=180°.
19.(6分)一个等腰三角形的周长为20,一边长为8,则其余两边长分别为多少?
20.(10分)如图,在△ABC中,AD是BC边上的高,CE平分∠ACB,若∠CAD=20°,∠B=50°,求∠AEC的度数.
21.(8分)现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是________.
研究(2):如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是________;
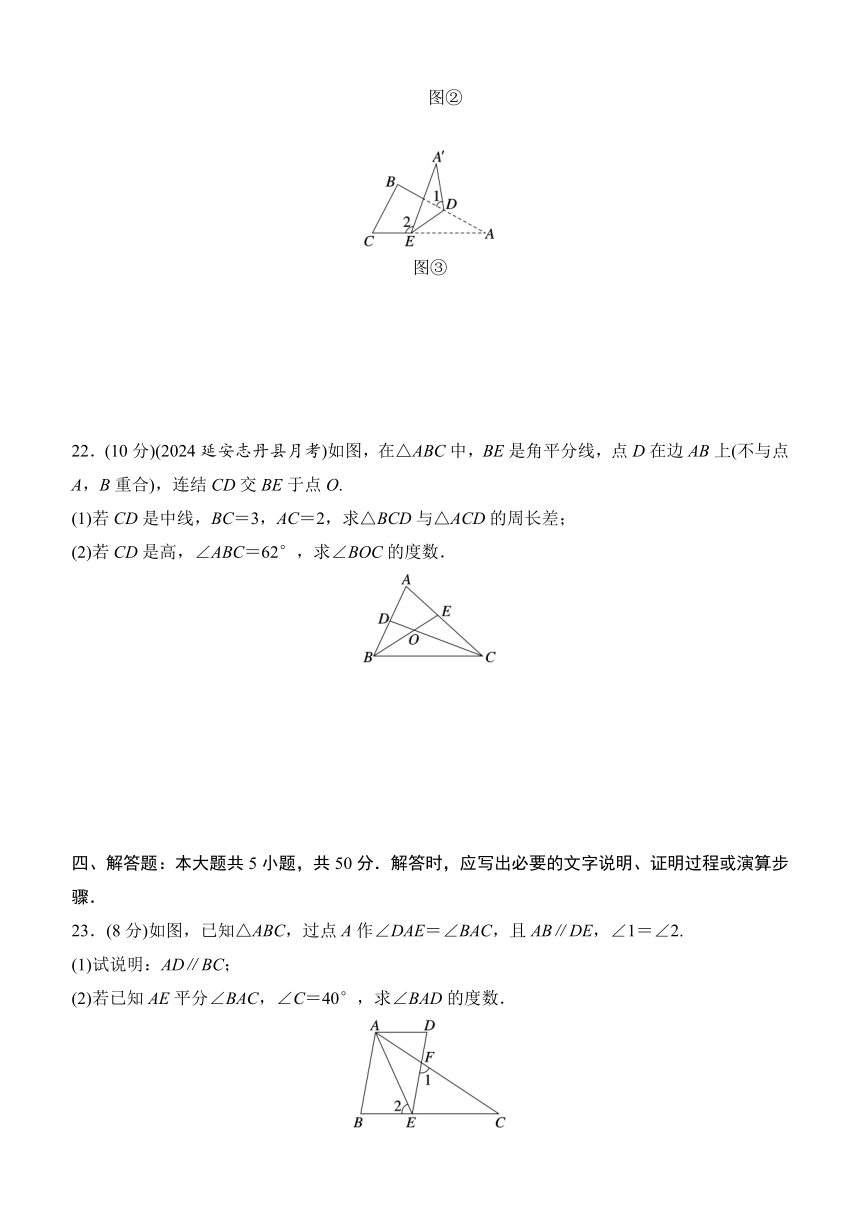
研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.
图①
图②
图③
22.(10分)(2024延安志丹县月考)如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O.
(1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差;
(2)若CD是高,∠ABC=62°,求∠BOC的度数.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,已知△ABC,过点A作∠DAE=∠BAC,且AB∥DE,∠1=∠2.
(1)试说明:AD∥BC;
(2)若已知AE平分∠BAC,∠C=40°,求∠BAD的度数.
24.(10分)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是________°.
(2)若这是个正多边形,则这个正多边形的一个内角是多少度?
25.(10分)(新情境)簪花结束后,小强和爸爸牵着妈妈的手,到蟳埔村参观游玩拍照纪念,精美的镂空窗花搭配蚵壳墙,极具泉州古民居特色,给小强一家留下了极其深刻的印象,在感叹泉州人民的勤劳与智慧的同时,聪明的小强发现有的窗花是由几种形状的正多边形组合镶嵌而成,具有很好的对称美,小强爸爸给他出了如下两个题目,请帮帮小强一起解决.
问题1.
已知一扇窗户在某个结点处由两种边长相等的正多边形镶嵌而成,其中一种是等边三角形,另一种不能是下列哪种形状的正多边形________.(填序号)
①正四边形;②正五边形; ③正六边形.
问题2.
小强发现某个花纹用4个相同的正八边形进行拼接,使相同的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图1.小强猜想,如果用n个相同的正六边形按这种方式进行拼接,如图2,若围成一圈后中间形成一个正多边形,则n的值为________,并简要说明理由.
26.(10分)若三角形的三边长分别是2、x、8,且x是不等式>-的正整数解,试求x的值.
27.(12分)(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图③,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
【详解答案】
1.C 解析:A.BE不是△ABC的高,不符合题意;B.BE不是△ABC的高,不符合题意;C.BE是△ABC的高,符合题意;D.BE不是△ABC的高,不符合题意.故选C.
2.C 解析:∵C选项中的伸缩门是利用了四边形的不稳定性,A、B、D选项都是利用了三角形的稳定性,∴选项C中的图片与众不同.故选C.
3.D 解析:∵∠DBA=105°,
∴∠ABC=180°-105°=75°.
∴∠A=∠ECA-∠ABC=125°-75°=50°.故选D.
4.C 解析:设这个多边形的边数为n,根据题意,得
(n-2)·180°=360°×4+180°,
解得n=11.则这个多边形的边数是11.故选C.
5.D 解析:三角形的两边长分别为2和5,设第三边的长为x,
∴5-2<x<5+2,即3<x<7.
∴第三边长可能为4,5,6,不可能为7.故选D.
6.C 解析:如图,设AC交DE于N,AC交DF于M,
由题意得∠EDF=45°,∠ACB=30°.
∵AC⊥DE,∴∠DNM=90°.
∴∠NMD=90°-∠NDM=45°.
∵∠NMD是△CMG的一个外角,∠ACB=30°,
∴∠CGM=∠NMD-∠ACB=15°.
∴∠BGF=180°-∠CGM=165°.故选C.
7.D 解析:∵一个正多边形的每一个外角都等于三角形内角和的,
∴多边形各外角都为30°.
设多边形的边数为n,∴30n=360.
解得n=12.故多边形的边数为12.故选D.
8.C 解析:由折叠可知∠B=∠DAB,∠BED=∠AED=90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠B+∠BAC+∠C=180°,∠C=60°,∴3∠B=120°.解得∠B=40°.∴∠BDE=90°-40°=50°.故选C.
9.B 解析:∵72÷8=9,∴360°÷9=40°.∴每次旋转的角度α=40°.故选B.
10.A 解析:如图,连结BE,
∵点D、E、F分别是BC、AD、EC的中点,
∴AE=DE=AD,EF=CF=CE,BD=DC=BC.
∵S△ABD=4,
∴S△ABD=S△ACD=4,
S△ABE=S△BED=S△ABD=2,S△AEC=S△CDE=S△ACD=2.
∴S△BEC=S△BDE+S△CDE=2+2=4.
∴S△BFC=S△BEF=S△BEC=×4=2.故选A.
11.40° 解析:∵∠ABD=∠A+∠C,
∴∠C=∠ABD-∠A=100°-60°=40°.
12.8 解析:∵多边形外角和是360°,正多边形的一个外角是45°,
∴360°÷45°=8,即该正多边形的边数为8.
13.10 解析:由三角形三边的关系可得PA-PB<AB<PA+PB.
∵PA=7 m,PB=5 m,
∴7-5<AB<7+5,即2 m<AB<12 m.
∵A、B间的距离长度为偶数,
∴A、B间的最大距离是10 m.
14.60 解析:∵P是∠ABC和∠ACB的平分线的交点.∴∠PBC=∠ABC,∠PCB=∠ACB.
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A.
∵∠P+∠PBC+∠PCB=180°,
∴∠P=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
∵∠P=2∠A,
∴2∠A=180°-(180°-∠A).
解得∠A=60°.
15. 360° 解析:如图,连结BE.
∵∠BGD=∠C+∠D,∠BGD=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB.
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F.
∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
16. 解析:∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD.
∵∠ACD是△ABC的外角,∠A1CD是△A1BC的外角,
∴∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1.
∴(∠A+∠ABC)=∠ABC+
∠A1.
∴∠A1=∠A,
∵∠A=θ,∴∠A1=.
同理可得∠A2=∠A1=,
∠A3=∠A2=,
……
∴∠An=.
∴∠A2 024=.
17.解:∵AB∥CD,
∴∠C=180°-∠B=180°-110°=70°.
∵五边形ABCDE内角和为(5-2)×180°=540°,
∴在五边形ABCDE中,∠E=540°-140°-110°-140°-70°=80°,
即x为80.
18.解:∵∠ABE=∠D,∠ABE+
∠ABC=180°,
∴∠ABC+∠D=180°.
又∵四边形内角和等于360°,
∴∠A+∠C=180°.
19.解:①若8为腰,设底为x,则有8+8+x=20,x=4(满足三边条件).
②若8为底,设腰为x,则有x+x+8=20,x=6(满足三边条件).
∴其余两边长是4和8或6和6.
20.解:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠CAD=20°,
∴∠ACD=90°-20°=70°.
∴∠BAC=180°-∠B-∠ACB=180°-50°-70°=60°.
∵CE平分∠ACB,
∴∠ACE=∠ACB=35°.
∴∠AEC=180°-∠EAC-∠ACE=180°-60°-35°=85°.
21.解:(1)∠1=2∠A
(2)∠1+∠2=2∠A
(3)∠2-∠1=2∠A.理由:
如图,设AB交A′E于点F,
∵∠2=∠AFE+∠A,∠AFE=∠A′+∠1,
∴∠2=∠A′+∠A+∠1.
∵∠A=∠A′,
∴∠2=2∠A+∠1.
∴∠2-∠1=2∠A.
22.解:(1)∵△BCD的周长为BC+CD+BD,△ACD的周长为AC+CD+AD,
∴△BCD与△ACD的周长差为BC-AC+BD-AD.
∵CD是△ABC的中线,
∴AD=BD.
又∵BC=3,AC=2,
∴BC-AC+BD-AD=BC-AC=3-2=1,即△BCD与△ACD的周长差为1.
(2)∵BE是∠ABC的平分线,∠ABC=62°,
∴∠ABE=∠ABC=×62°=31°.
∵CD是△ABC的高,
∴∠CDB=90°.
∴∠BOC=∠CDB+∠ABE=90°+31°=121°.
23.解:(1)∵AB∥DE,
∴∠BAC=∠1.
∵∠1=∠2,
∴∠BAC=∠2.
∵∠DAE=∠BAC,
∴∠DAE=∠2.
∴AD∥BC.
(2)∵∠DAE=∠BAC,
∴∠BAE=∠DAC.
∵AD∥BC,
∴∠C=∠DAC.
∴∠C=∠BAE=∠DAC=40°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°.
∴∠BAD=∠BAC+∠CAD=120°.
24.解:(1)30
(2)由(1)知,这个多边形是正十二边形,
所以这个正多边形的一个内角是180°-=150°.
25.解:问题1:②
问题2:6
理由如下:由题意得,这n个正六边形围成的图形是一个正多边形.由图2可知,围成的这个正多边形的每个内角的度数是120°.
所以(n-2)180°=120°n.
解得n=6.
26.解:>-,3(x+2)>-2(1-2x),
解得x<8.
∵x是它的正整数解,
∴x可取1,2,3,4,5,6,7.
根据三角形的三边关系,
得8-2<x<8+2,即6<x<10.∴x=7.
27.解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=×240°=120°.
∴∠E=180°-(∠ADE+
∠DAE)=180°-120°=60°.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.如图,BE是△ABC的高的是( )
A B
C D
2.(新情境)从数学角度看下列四幅图片有一个与众不同,该图片是( )
3.如图,∠DBA=105°,∠ECA=125°,则∠A的度数是( )
A.75° B.60° C.55° D.50°
4.一个多边形,它的内角和比外角和的4倍多180°,则这个多边形的边数是( )
A.9 B.10 C.11 D.12
5.(2024武威凉州区期中)已知三角形的两边长分别为2和5,则第三边长不可能是( )
A.4 B.5 C.6 D.7
6.将一副三角板按如图所示的方式摆放,DE经过点B,AC⊥DE,BC与DF交于点G,则∠BGF的度数为( )
A.15° B.135° C.165° D.155°
7.若一个正多边形的每一个外角都等于三角形内角和的,则这个正多边形为( )
A.六边形 B.八边形
C.十边形 D.十二边形
8.如图,在△ABC中,∠C=60°,把△ABC沿直线DE折叠,使得点B与点A重合.若AD恰好平分∠BAC,则∠BDE的度数为( )
A.30° B.40° C.50° D.60°
9.如图,大建从A点出发沿直线前进8 m到达点B后向左旋转的角度为α,再沿直线前进8 m,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72 m,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
10.如图,△ABC中,D、E、F分别是BC、AD、EC的中点,若S△ABD=4,则S△BFC=( )
A.2 B.1 C. D.
二、填空题:本大题共6小题,每小题4分,共24分.
11.如图,点D是△ABC的边CB延长线上一点,若∠ABD=100°,∠A=60°,则∠C=________.
12.(2024重庆B卷中考)若正多边形的一个外角是45°,则这个正多边形的边数为________.
13.如图,为估计池塘两岸A、B两点间的距离,小奇在池塘一侧选取了一点P.分别测得PA=7 m,PB=5 m,若A、B间的距离长度为偶数(单位:m),那么A、B间的最大距离是________m.
14.如图,在△ABC中,P是∠ABC和∠ACB的平分线的交点.若∠P=2∠A,则∠A=________°.
15.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为________.
16.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An,设∠A=θ,则∠A2 024=________.
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,已知五边形ABCDE中,AB∥CD,求x的值.
18.(6分)(2024淮安期末)如图,∠ABE是四边形ABCD的外角,已知∠ABE=∠D.
试说明:∠A+∠C=180°.
19.(6分)一个等腰三角形的周长为20,一边长为8,则其余两边长分别为多少?
20.(10分)如图,在△ABC中,AD是BC边上的高,CE平分∠ACB,若∠CAD=20°,∠B=50°,求∠AEC的度数.
21.(8分)现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是________.
研究(2):如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是________;
研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.
图①
图②
图③
22.(10分)(2024延安志丹县月考)如图,在△ABC中,BE是角平分线,点D在边AB上(不与点A,B重合),连结CD交BE于点O.
(1)若CD是中线,BC=3,AC=2,求△BCD与△ACD的周长差;
(2)若CD是高,∠ABC=62°,求∠BOC的度数.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,已知△ABC,过点A作∠DAE=∠BAC,且AB∥DE,∠1=∠2.
(1)试说明:AD∥BC;
(2)若已知AE平分∠BAC,∠C=40°,求∠BAD的度数.
24.(10分)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是________°.
(2)若这是个正多边形,则这个正多边形的一个内角是多少度?
25.(10分)(新情境)簪花结束后,小强和爸爸牵着妈妈的手,到蟳埔村参观游玩拍照纪念,精美的镂空窗花搭配蚵壳墙,极具泉州古民居特色,给小强一家留下了极其深刻的印象,在感叹泉州人民的勤劳与智慧的同时,聪明的小强发现有的窗花是由几种形状的正多边形组合镶嵌而成,具有很好的对称美,小强爸爸给他出了如下两个题目,请帮帮小强一起解决.
问题1.
已知一扇窗户在某个结点处由两种边长相等的正多边形镶嵌而成,其中一种是等边三角形,另一种不能是下列哪种形状的正多边形________.(填序号)
①正四边形;②正五边形; ③正六边形.
问题2.
小强发现某个花纹用4个相同的正八边形进行拼接,使相同的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图1.小强猜想,如果用n个相同的正六边形按这种方式进行拼接,如图2,若围成一圈后中间形成一个正多边形,则n的值为________,并简要说明理由.
26.(10分)若三角形的三边长分别是2、x、8,且x是不等式>-的正整数解,试求x的值.
27.(12分)(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图③,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
【详解答案】
1.C 解析:A.BE不是△ABC的高,不符合题意;B.BE不是△ABC的高,不符合题意;C.BE是△ABC的高,符合题意;D.BE不是△ABC的高,不符合题意.故选C.
2.C 解析:∵C选项中的伸缩门是利用了四边形的不稳定性,A、B、D选项都是利用了三角形的稳定性,∴选项C中的图片与众不同.故选C.
3.D 解析:∵∠DBA=105°,
∴∠ABC=180°-105°=75°.
∴∠A=∠ECA-∠ABC=125°-75°=50°.故选D.
4.C 解析:设这个多边形的边数为n,根据题意,得
(n-2)·180°=360°×4+180°,
解得n=11.则这个多边形的边数是11.故选C.
5.D 解析:三角形的两边长分别为2和5,设第三边的长为x,
∴5-2<x<5+2,即3<x<7.
∴第三边长可能为4,5,6,不可能为7.故选D.
6.C 解析:如图,设AC交DE于N,AC交DF于M,
由题意得∠EDF=45°,∠ACB=30°.
∵AC⊥DE,∴∠DNM=90°.
∴∠NMD=90°-∠NDM=45°.
∵∠NMD是△CMG的一个外角,∠ACB=30°,
∴∠CGM=∠NMD-∠ACB=15°.
∴∠BGF=180°-∠CGM=165°.故选C.
7.D 解析:∵一个正多边形的每一个外角都等于三角形内角和的,
∴多边形各外角都为30°.
设多边形的边数为n,∴30n=360.
解得n=12.故多边形的边数为12.故选D.
8.C 解析:由折叠可知∠B=∠DAB,∠BED=∠AED=90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵∠B+∠BAC+∠C=180°,∠C=60°,∴3∠B=120°.解得∠B=40°.∴∠BDE=90°-40°=50°.故选C.
9.B 解析:∵72÷8=9,∴360°÷9=40°.∴每次旋转的角度α=40°.故选B.
10.A 解析:如图,连结BE,
∵点D、E、F分别是BC、AD、EC的中点,
∴AE=DE=AD,EF=CF=CE,BD=DC=BC.
∵S△ABD=4,
∴S△ABD=S△ACD=4,
S△ABE=S△BED=S△ABD=2,S△AEC=S△CDE=S△ACD=2.
∴S△BEC=S△BDE+S△CDE=2+2=4.
∴S△BFC=S△BEF=S△BEC=×4=2.故选A.
11.40° 解析:∵∠ABD=∠A+∠C,
∴∠C=∠ABD-∠A=100°-60°=40°.
12.8 解析:∵多边形外角和是360°,正多边形的一个外角是45°,
∴360°÷45°=8,即该正多边形的边数为8.
13.10 解析:由三角形三边的关系可得PA-PB<AB<PA+PB.
∵PA=7 m,PB=5 m,
∴7-5<AB<7+5,即2 m<AB<12 m.
∵A、B间的距离长度为偶数,
∴A、B间的最大距离是10 m.
14.60 解析:∵P是∠ABC和∠ACB的平分线的交点.∴∠PBC=∠ABC,∠PCB=∠ACB.
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A.
∵∠P+∠PBC+∠PCB=180°,
∴∠P=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
∵∠P=2∠A,
∴2∠A=180°-(180°-∠A).
解得∠A=60°.
15. 360° 解析:如图,连结BE.
∵∠BGD=∠C+∠D,∠BGD=∠CBE+∠DEB,
∴∠C+∠D=∠CBE+∠DEB.
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F.
∵∠A+∠ABE+∠BEF+∠F=360°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
16. 解析:∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD.
∵∠ACD是△ABC的外角,∠A1CD是△A1BC的外角,
∴∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1.
∴(∠A+∠ABC)=∠ABC+
∠A1.
∴∠A1=∠A,
∵∠A=θ,∴∠A1=.
同理可得∠A2=∠A1=,
∠A3=∠A2=,
……
∴∠An=.
∴∠A2 024=.
17.解:∵AB∥CD,
∴∠C=180°-∠B=180°-110°=70°.
∵五边形ABCDE内角和为(5-2)×180°=540°,
∴在五边形ABCDE中,∠E=540°-140°-110°-140°-70°=80°,
即x为80.
18.解:∵∠ABE=∠D,∠ABE+
∠ABC=180°,
∴∠ABC+∠D=180°.
又∵四边形内角和等于360°,
∴∠A+∠C=180°.
19.解:①若8为腰,设底为x,则有8+8+x=20,x=4(满足三边条件).
②若8为底,设腰为x,则有x+x+8=20,x=6(满足三边条件).
∴其余两边长是4和8或6和6.
20.解:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠CAD=20°,
∴∠ACD=90°-20°=70°.
∴∠BAC=180°-∠B-∠ACB=180°-50°-70°=60°.
∵CE平分∠ACB,
∴∠ACE=∠ACB=35°.
∴∠AEC=180°-∠EAC-∠ACE=180°-60°-35°=85°.
21.解:(1)∠1=2∠A
(2)∠1+∠2=2∠A
(3)∠2-∠1=2∠A.理由:
如图,设AB交A′E于点F,
∵∠2=∠AFE+∠A,∠AFE=∠A′+∠1,
∴∠2=∠A′+∠A+∠1.
∵∠A=∠A′,
∴∠2=2∠A+∠1.
∴∠2-∠1=2∠A.
22.解:(1)∵△BCD的周长为BC+CD+BD,△ACD的周长为AC+CD+AD,
∴△BCD与△ACD的周长差为BC-AC+BD-AD.
∵CD是△ABC的中线,
∴AD=BD.
又∵BC=3,AC=2,
∴BC-AC+BD-AD=BC-AC=3-2=1,即△BCD与△ACD的周长差为1.
(2)∵BE是∠ABC的平分线,∠ABC=62°,
∴∠ABE=∠ABC=×62°=31°.
∵CD是△ABC的高,
∴∠CDB=90°.
∴∠BOC=∠CDB+∠ABE=90°+31°=121°.
23.解:(1)∵AB∥DE,
∴∠BAC=∠1.
∵∠1=∠2,
∴∠BAC=∠2.
∵∠DAE=∠BAC,
∴∠DAE=∠2.
∴AD∥BC.
(2)∵∠DAE=∠BAC,
∴∠BAE=∠DAC.
∵AD∥BC,
∴∠C=∠DAC.
∴∠C=∠BAE=∠DAC=40°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°.
∴∠BAD=∠BAC+∠CAD=120°.
24.解:(1)30
(2)由(1)知,这个多边形是正十二边形,
所以这个正多边形的一个内角是180°-=150°.
25.解:问题1:②
问题2:6
理由如下:由题意得,这n个正六边形围成的图形是一个正多边形.由图2可知,围成的这个正多边形的每个内角的度数是120°.
所以(n-2)180°=120°n.
解得n=6.
26.解:>-,3(x+2)>-2(1-2x),
解得x<8.
∵x是它的正整数解,
∴x可取1,2,3,4,5,6,7.
根据三角形的三边关系,
得8-2<x<8+2,即6<x<10.∴x=7.
27.解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=×240°=120°.
∴∠E=180°-(∠ADE+
∠DAE)=180°-120°=60°.
