17.1 勾股定理 第2课时 勾股定理的应用 课件(共16张PPT)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 17.1 勾股定理 第2课时 勾股定理的应用 课件(共16张PPT)2024-2025学年人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 15:00:53 | ||
图片预览





文档简介
(共16张PPT)
17.1 勾股定理
第十七章 勾股定理
课程讲授
新知导入
随堂练习
课堂小结
勾股定理的应用
知识要点
1.利用勾股定理解决实际问题
2.构造直角三角形解决实际问题
新知导入
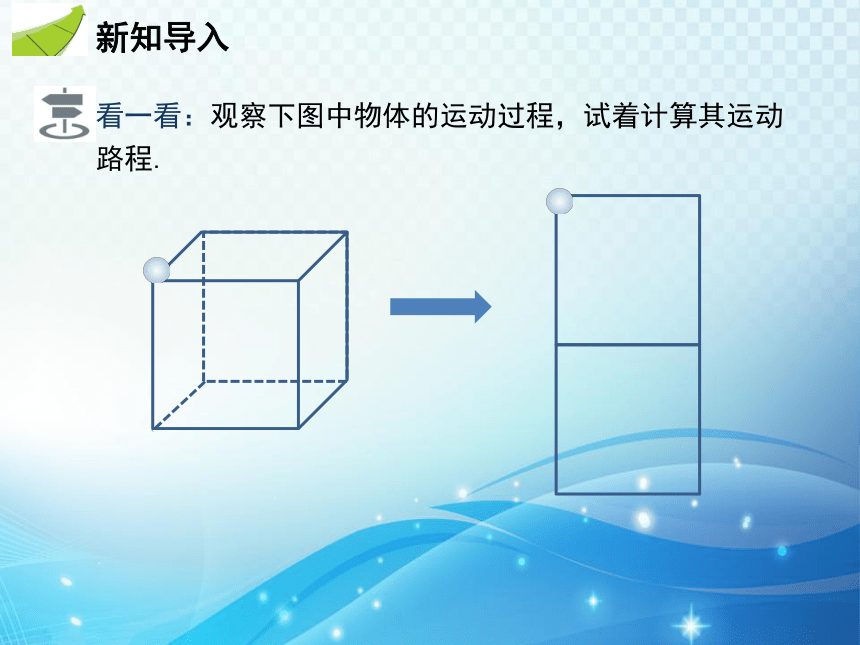
看一看:观察下图中物体的运动过程,试着计算其运动路程.
课程讲授
1
利用勾股定理解决实际问题
在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=12+22=5.
AC= ≈2. 24.因为AC大于木板的宽2.2 m,所以木板能从门框内通过.
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什
么?
解:
分析:可以看出,木板横着或竖着都不能从门框内通过,
只能试试斜着能否通过.门框对角线AC的长度是斜着能
通过的最大长度.求出AC,再与木板的宽比较,就能知
道木板能否通过.
课程讲授
1
利用勾股定理解决实际问题
解:可以看出,BD=OD-OB.
在Rt△AOB中,根据勾股定理,得 OB2=AB2-OA2=2.62-2.42 = 1,OB= =1.
在Rt△COD中,根据勾股定理,得OD2=CD2-OC2=2.62-(2.4-
0.5)2=3.15, OD = ≈1. 77, BD=OD-OB≈l.77-1=0.77.
所以梯子的顶端沿墙下滑0.5 m时,梯子底端并不是也外移
0.5 m,而是外移约0.77 m.
例2 如图, 一架2. 6 m长的梯子AB斜靠在一竖直
的墙AO上,这时AO为2. 4 m.如果梯子的顶端A
沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?
课程讲授
1
利用勾股定理解决实际问题
练一练:
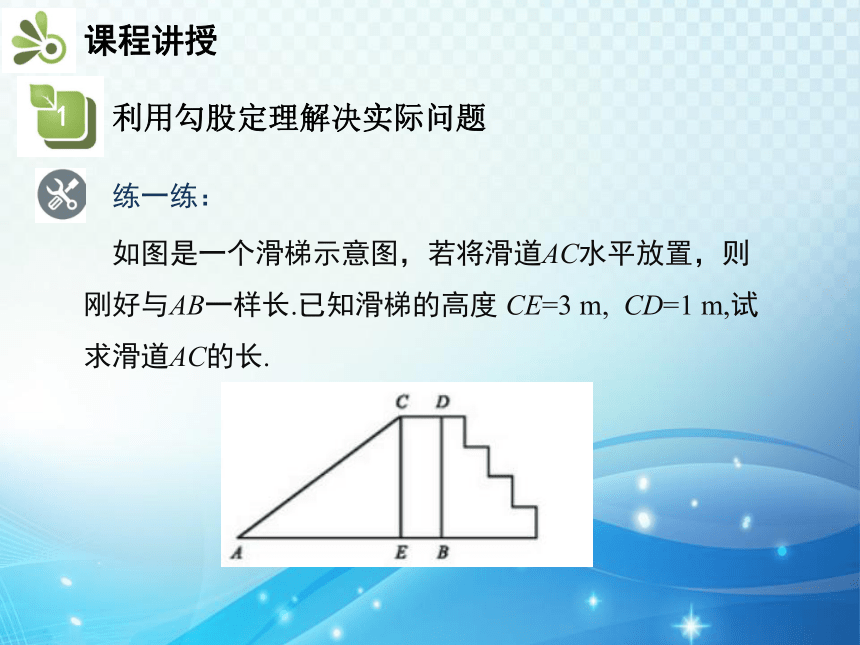
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度 CE=3 m, CD=1 m,试求滑道AC的长.
课程讲授
1
利用勾股定理解决实际问题
练一练:
解:设滑道AC的长度为x m,则AB的长度为x m,
AE的长度为(x-1)m,
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,即(x-1)2+32=x2,
解得x=5.故滑道AC的长度为5 m.
课程讲授
2
构造直角三角形解决实际问题
例3 假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们在点A登陆后先 往东走8 km到达C处,又往北走了2 km,遇到障碍后又往西走了3 km,再往北走了6 km后往东拐,仅走了1 km就找到了藏宝
点B,如图,登陆点A到藏宝点B的距离
是________.
10 km
课程讲授
例4 一辆装满货物的卡车,其外形高2.5 m,宽1.6 m,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由.
A
B
N
M
2 m
2.3m
解:在Rt△OCD中,∠CDO=90°,由勾股定理,得
O
H
C
D
CD=
CH=0.6+2.3=2.9( m)>2.5(m).
答:卡车能通过厂门.
2
构造直角三角形解决实际问题
课程讲授
(中考·安顺)如图,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8 m
B.10 m
C.12 m
D.14 m
练一练:
B
2
构造直角三角形解决实际问题
课程讲授
归纳:利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
2
构造直角三角形解决实际问题
随堂练习
1.如图,一轮船以16 n mile/h的速度从港口A出发向东北方向航行,另一轮船以12 n mile/h的速度同时从港口A出发向东南方向航行,离开港口2 h后,则两船相距( )
A.25 n mile
B.30 n mile
C.40 n mile
D.50 n mile
C
随堂练习
2.(中考·绍兴)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为( )
A.0.7 m B.1.5 m
C.2.2 m D.2.4 m
C
随堂练习
3. (中考·厦门)已知A,B,C三地位置如图所示,
∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是________;若A地在C地的正东方向,则B地在C地的________方向.
5 km
正北
随堂练习
4.如图,在△ABC中,AB=AC,D点在CB 延长线上,
求证:AD2-AB2=BD·CD.
A
B
C
D
E
证明:过A作AE⊥BC于E.
∵AB=AC,∴BE=CE.
在Rt △ADE中,AD2=AE2+DE2.
在Rt △ABE中,AB2=AE2+BE2.
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD.
课堂小结
勾股定理的应用
利用勾股定理解决实际问题
构造直角三角形解决实际问题
17.1 勾股定理
第十七章 勾股定理
课程讲授
新知导入
随堂练习
课堂小结
勾股定理的应用
知识要点
1.利用勾股定理解决实际问题
2.构造直角三角形解决实际问题
新知导入
看一看:观察下图中物体的运动过程,试着计算其运动路程.
课程讲授
1
利用勾股定理解决实际问题
在Rt△ABC中,根据勾股定理,AC2=AB2+BC2=12+22=5.
AC= ≈2. 24.因为AC大于木板的宽2.2 m,所以木板能从门框内通过.
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什
么?
解:
分析:可以看出,木板横着或竖着都不能从门框内通过,
只能试试斜着能否通过.门框对角线AC的长度是斜着能
通过的最大长度.求出AC,再与木板的宽比较,就能知
道木板能否通过.
课程讲授
1
利用勾股定理解决实际问题
解:可以看出,BD=OD-OB.
在Rt△AOB中,根据勾股定理,得 OB2=AB2-OA2=2.62-2.42 = 1,OB= =1.
在Rt△COD中,根据勾股定理,得OD2=CD2-OC2=2.62-(2.4-
0.5)2=3.15, OD = ≈1. 77, BD=OD-OB≈l.77-1=0.77.
所以梯子的顶端沿墙下滑0.5 m时,梯子底端并不是也外移
0.5 m,而是外移约0.77 m.
例2 如图, 一架2. 6 m长的梯子AB斜靠在一竖直
的墙AO上,这时AO为2. 4 m.如果梯子的顶端A
沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?
课程讲授
1
利用勾股定理解决实际问题
练一练:
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度 CE=3 m, CD=1 m,试求滑道AC的长.
课程讲授
1
利用勾股定理解决实际问题
练一练:
解:设滑道AC的长度为x m,则AB的长度为x m,
AE的长度为(x-1)m,
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,即(x-1)2+32=x2,
解得x=5.故滑道AC的长度为5 m.
课程讲授
2
构造直角三角形解决实际问题
例3 假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们在点A登陆后先 往东走8 km到达C处,又往北走了2 km,遇到障碍后又往西走了3 km,再往北走了6 km后往东拐,仅走了1 km就找到了藏宝
点B,如图,登陆点A到藏宝点B的距离
是________.
10 km
课程讲授
例4 一辆装满货物的卡车,其外形高2.5 m,宽1.6 m,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由.
A
B
N
M
2 m
2.3m
解:在Rt△OCD中,∠CDO=90°,由勾股定理,得
O
H
C
D
CD=
CH=0.6+2.3=2.9( m)>2.5(m).
答:卡车能通过厂门.
2
构造直角三角形解决实际问题
课程讲授
(中考·安顺)如图,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( )
A.8 m
B.10 m
C.12 m
D.14 m
练一练:
B
2
构造直角三角形解决实际问题
课程讲授
归纳:利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
2
构造直角三角形解决实际问题
随堂练习
1.如图,一轮船以16 n mile/h的速度从港口A出发向东北方向航行,另一轮船以12 n mile/h的速度同时从港口A出发向东南方向航行,离开港口2 h后,则两船相距( )
A.25 n mile
B.30 n mile
C.40 n mile
D.50 n mile
C
随堂练习
2.(中考·绍兴)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为( )
A.0.7 m B.1.5 m
C.2.2 m D.2.4 m
C
随堂练习
3. (中考·厦门)已知A,B,C三地位置如图所示,
∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是________;若A地在C地的正东方向,则B地在C地的________方向.
5 km
正北
随堂练习
4.如图,在△ABC中,AB=AC,D点在CB 延长线上,
求证:AD2-AB2=BD·CD.
A
B
C
D
E
证明:过A作AE⊥BC于E.
∵AB=AC,∴BE=CE.
在Rt △ADE中,AD2=AE2+DE2.
在Rt △ABE中,AB2=AE2+BE2.
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD.
课堂小结
勾股定理的应用
利用勾股定理解决实际问题
构造直角三角形解决实际问题
