湖南省邵阳县2015-2016学年八年级下学期期中质量检测数学试题
文档属性
| 名称 | 湖南省邵阳县2015-2016学年八年级下学期期中质量检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-03 19:11:36 | ||
图片预览


文档简介
邵阳县2016年上期八年级期中质量检测试卷
数 学
精心选一选:(将正确答案的序号填在后面的括号中,3×10=30分)
1、下列图形中是中心对称图形的是( ):
A、①②④; B、②③④; C、①③④; D、①②③;
2.下列几组数中,能作为直角三角形三边长度的是 ( )
A. 4,5,6 B.1,1, C. 6,8,12 D. 5,12,17
3、下列命题中,假命题是( )。
A、对角线相等的平行四边形是矩形 B、四条边都相等的平行四边形是正方形
C、既是菱形又是矩形的四边形是正方形 D、对角线互相垂直的平行四边形是菱形
4、如右下图所示,已知在三角形纸片ABC ( http: / / www.21cnjy.com )中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( ).
A、3 B. C. D.2
5.一个多边形的内角和等于外角和的一半,那么这个多边形是 ( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
6、如右下图所示,在□ABCD中,已知∠ODA=90 , AC=10cm,BD=6cm,则AD的长为( ).
A、4cm B、5cm C、6cm D、8cm
7、矩形、菱形、正方形都具有的性质是( )
A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角
8.如图,四边形ABCD的对角线互相平分,要使它变为矩形,
需要添加的条件是( )
A. AB=CD B. AD=BC C. AB=BC D. AC=BD
9.如图(与第8题图同),四边形ABCD中 ( http: / / www.21cnjy.com ),对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.4组
10. 如图,边长为6的大正方形中有两个小正方形,若
两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D. 19
二、细心填一填:(3×8=24分)
11、四边形具有不稳定性,请举一个应用四边形不稳定性的实例: 。
12、顺次连结任意四边形各边中点所得到的四边形一定是 .
13.一个直角三角形的三边为3,4,x,则x= 。
14. 用边长分别为3cm,5cm,7cm的两个全等三角形能拼成 个不同的平行四边形。
15.如右下图所示,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=3,DC=,则△ABC的面积是________.
16.已知在△ABC中,AD⊥BC,垂足为点D,DE//AC交AB于E,DF//AB交AC于F,
当△A BC再添加一个条件: 时,四边形AEDF为菱形(填写一个条件即可)。
17.如图,△ABC中,∠C为直角,射线AD平分∠BAC交BC于点D,BD∶DC=2∶1,BC=3.6cm,则点D到AB边的距离为 cm。
18. 如图,在Rt△ABC中,∠ACB= ( http: / / www.21cnjy.com )90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有 个。
(第15题) (第17题) (第18题)
三、耐心做一做(共60分)
19、已知:□ABCD的周 ( http: / / www.21cnjy.com )长为50 cm,对角线AC、BD相交于点O,△AOD的周长比△BOA的周长长5 cm,求这个平行四边形各边的长. (8分) A D
O
B C
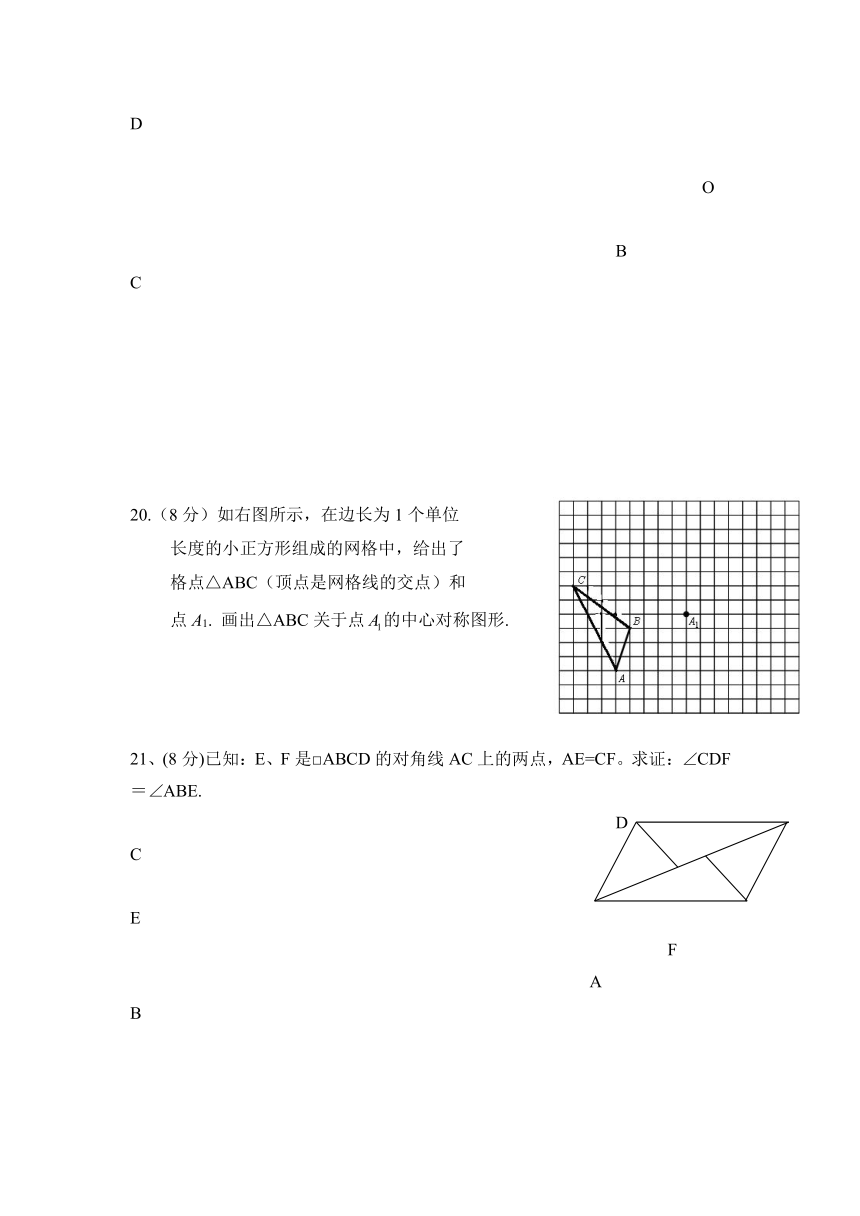
20.(8分)如右图所示,在边长为1个单位
长度的小正方形组成的网格中,给出了
格点△ABC(顶点是网格线的交点)和
点A1. 画出△ABC关于点的中心对称图形.
21、(8分)已知:E、F是□ABCD的对角线AC上的两点,AE=CF。求证:∠CDF=∠ABE.
D C
E
F
A B
22.(8分)如图所示,为了躲避海 ( http: / / www.21cnjy.com )盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
23.(8分)已知:如右下图所示,四边形ABCD是由两个全等的等边三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.
24、(8分)在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm.求:
(1)两条对角线的长度;(2)菱形的面积.
25.(8分)如图,已知:在Rt△ ( http: / / www.21cnjy.com )ABC中,AC⊥BC,CD⊥AB于D,AG平分∠BAC,交BC于G,交CD于E,EF∥AB交BC于F,求证:CE=BF.
26.(10分)如图所示,在ΔABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
①求证:OE=OF;
②当点O运动到何处时,四边形AECF是矩形?并请说明理由。
③当点O运动到AC边的中点时,在ΔABC中添加一个什么条件后,四边形AECF是正方形。(只需写出一个条件,不必证明)
参考答案:一、1、C;2、B;3、B;4、D;5、A;6、A;7、B;8、D;9、C;10、B;
二、11、电动伸缩门;(答案不唯一)12、平行四边形;13、5或;14、3;15、;16、AB=AC;17、1.2;18、6;
三、19、AD=10cm,AB=5cm;
20、略
21、由已知条件可证得:△BAE≌△DCF(SAS),∴∠CDF=∠ABE。
22、过点P作PC⊥AB于点C,∠PAB=15°,∠APB=15°,
∴BA=BP=2×20=40海里。
在Rt△PBC中,PC=BP=20海里<22海里。故,该船无触礁危险。
23、∵△ABD和△BCD是全等的两个正三角形。
∴AD=BD=AB=BC,∠ABD=∠DBC=60°,∴MD∥BN,
又∵M是AD的中点,∴MD=AD,
同理:BN=BC,∴MD=BN,∴四边形BMDN是平行四边形。
MB⊥AD,∠DMB=90°,∴四边形BMDN是矩形。
24、(1)∵菱形ABCD的周长是48cm,
∴AB=BC=CD=DA=12cm,
又∵∠ABC与∠BAD的度数比为1:2,∠ABC=60°,
∴△ABC是正三角形,AC=AB=12cm,又∠ABO=30°,
∴AO=6cm,BO=cm,BD=cm,
(2)S菱形ABCD=AC·BD=cm2.
25、证明:过点E作EH∥BC交AB于点H,则,四边形EHBF是平行四边形,EH=BF,
∵∠ACD+∠BCD=90°,∠DBC+∠BCD=90°,
∴∠ACD=∠DBC,又∵∠AHE=∠DBC,∴∠AHE=∠ACF,
在△ACE和△AHE中,∠AHE=∠ACF,
∠ACD=∠DBC
AE=AE
∴△ACE≌△AHE(AAS),∴EH=CE,又EH=BF,∴CE=BF
26、(1)证明:∵CE平分∠ACB,∴∠ACE=∠BCE,
∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理:OF=OC,
∴OE=OF.
(2)当点O运动到AC的中点时,四边形AECF是矩形;
理由:如图,AO=CO,EO=FO,∴四边形AECF是平行四边形;
∵CE平分∠ACB,∴∠ACE=∠ACB,同理:∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)= ×180°=90°
∴四边形AECF是平行矩形;
(3)添加∠ACB=90°.
①
②
③
④
北x北
60°
B
75°
东
A
P
B
C
D
E
F
A
G
数 学
精心选一选:(将正确答案的序号填在后面的括号中,3×10=30分)
1、下列图形中是中心对称图形的是( ):
A、①②④; B、②③④; C、①③④; D、①②③;
2.下列几组数中,能作为直角三角形三边长度的是 ( )
A. 4,5,6 B.1,1, C. 6,8,12 D. 5,12,17
3、下列命题中,假命题是( )。
A、对角线相等的平行四边形是矩形 B、四条边都相等的平行四边形是正方形
C、既是菱形又是矩形的四边形是正方形 D、对角线互相垂直的平行四边形是菱形
4、如右下图所示,已知在三角形纸片ABC ( http: / / www.21cnjy.com )中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( ).
A、3 B. C. D.2
5.一个多边形的内角和等于外角和的一半,那么这个多边形是 ( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
6、如右下图所示,在□ABCD中,已知∠ODA=90 , AC=10cm,BD=6cm,则AD的长为( ).
A、4cm B、5cm C、6cm D、8cm
7、矩形、菱形、正方形都具有的性质是( )
A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角
8.如图,四边形ABCD的对角线互相平分,要使它变为矩形,
需要添加的条件是( )
A. AB=CD B. AD=BC C. AB=BC D. AC=BD
9.如图(与第8题图同),四边形ABCD中 ( http: / / www.21cnjy.com ),对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.4组
10. 如图,边长为6的大正方形中有两个小正方形,若
两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D. 19
二、细心填一填:(3×8=24分)
11、四边形具有不稳定性,请举一个应用四边形不稳定性的实例: 。
12、顺次连结任意四边形各边中点所得到的四边形一定是 .
13.一个直角三角形的三边为3,4,x,则x= 。
14. 用边长分别为3cm,5cm,7cm的两个全等三角形能拼成 个不同的平行四边形。
15.如右下图所示,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=3,DC=,则△ABC的面积是________.
16.已知在△ABC中,AD⊥BC,垂足为点D,DE//AC交AB于E,DF//AB交AC于F,
当△A BC再添加一个条件: 时,四边形AEDF为菱形(填写一个条件即可)。
17.如图,△ABC中,∠C为直角,射线AD平分∠BAC交BC于点D,BD∶DC=2∶1,BC=3.6cm,则点D到AB边的距离为 cm。
18. 如图,在Rt△ABC中,∠ACB= ( http: / / www.21cnjy.com )90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有 个。
(第15题) (第17题) (第18题)
三、耐心做一做(共60分)
19、已知:□ABCD的周 ( http: / / www.21cnjy.com )长为50 cm,对角线AC、BD相交于点O,△AOD的周长比△BOA的周长长5 cm,求这个平行四边形各边的长. (8分) A D
O
B C
20.(8分)如右图所示,在边长为1个单位
长度的小正方形组成的网格中,给出了
格点△ABC(顶点是网格线的交点)和
点A1. 画出△ABC关于点的中心对称图形.
21、(8分)已知:E、F是□ABCD的对角线AC上的两点,AE=CF。求证:∠CDF=∠ABE.
D C
E
F
A B
22.(8分)如图所示,为了躲避海 ( http: / / www.21cnjy.com )盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
23.(8分)已知:如右下图所示,四边形ABCD是由两个全等的等边三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.
24、(8分)在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm.求:
(1)两条对角线的长度;(2)菱形的面积.
25.(8分)如图,已知:在Rt△ ( http: / / www.21cnjy.com )ABC中,AC⊥BC,CD⊥AB于D,AG平分∠BAC,交BC于G,交CD于E,EF∥AB交BC于F,求证:CE=BF.
26.(10分)如图所示,在ΔABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
①求证:OE=OF;
②当点O运动到何处时,四边形AECF是矩形?并请说明理由。
③当点O运动到AC边的中点时,在ΔABC中添加一个什么条件后,四边形AECF是正方形。(只需写出一个条件,不必证明)
参考答案:一、1、C;2、B;3、B;4、D;5、A;6、A;7、B;8、D;9、C;10、B;
二、11、电动伸缩门;(答案不唯一)12、平行四边形;13、5或;14、3;15、;16、AB=AC;17、1.2;18、6;
三、19、AD=10cm,AB=5cm;
20、略
21、由已知条件可证得:△BAE≌△DCF(SAS),∴∠CDF=∠ABE。
22、过点P作PC⊥AB于点C,∠PAB=15°,∠APB=15°,
∴BA=BP=2×20=40海里。
在Rt△PBC中,PC=BP=20海里<22海里。故,该船无触礁危险。
23、∵△ABD和△BCD是全等的两个正三角形。
∴AD=BD=AB=BC,∠ABD=∠DBC=60°,∴MD∥BN,
又∵M是AD的中点,∴MD=AD,
同理:BN=BC,∴MD=BN,∴四边形BMDN是平行四边形。
MB⊥AD,∠DMB=90°,∴四边形BMDN是矩形。
24、(1)∵菱形ABCD的周长是48cm,
∴AB=BC=CD=DA=12cm,
又∵∠ABC与∠BAD的度数比为1:2,∠ABC=60°,
∴△ABC是正三角形,AC=AB=12cm,又∠ABO=30°,
∴AO=6cm,BO=cm,BD=cm,
(2)S菱形ABCD=AC·BD=cm2.
25、证明:过点E作EH∥BC交AB于点H,则,四边形EHBF是平行四边形,EH=BF,
∵∠ACD+∠BCD=90°,∠DBC+∠BCD=90°,
∴∠ACD=∠DBC,又∵∠AHE=∠DBC,∴∠AHE=∠ACF,
在△ACE和△AHE中,∠AHE=∠ACF,
∠ACD=∠DBC
AE=AE
∴△ACE≌△AHE(AAS),∴EH=CE,又EH=BF,∴CE=BF
26、(1)证明:∵CE平分∠ACB,∴∠ACE=∠BCE,
∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理:OF=OC,
∴OE=OF.
(2)当点O运动到AC的中点时,四边形AECF是矩形;
理由:如图,AO=CO,EO=FO,∴四边形AECF是平行四边形;
∵CE平分∠ACB,∴∠ACE=∠ACB,同理:∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)= ×180°=90°
∴四边形AECF是平行矩形;
(3)添加∠ACB=90°.
①
②
③
④
北x北
60°
B
75°
东
A
P
B
C
D
E
F
A
G
同课章节目录
