七年级下学期数学期末考试测试试题(含答案)(新北师大版)
文档属性
| 名称 | 七年级下学期数学期末考试测试试题(含答案)(新北师大版) | 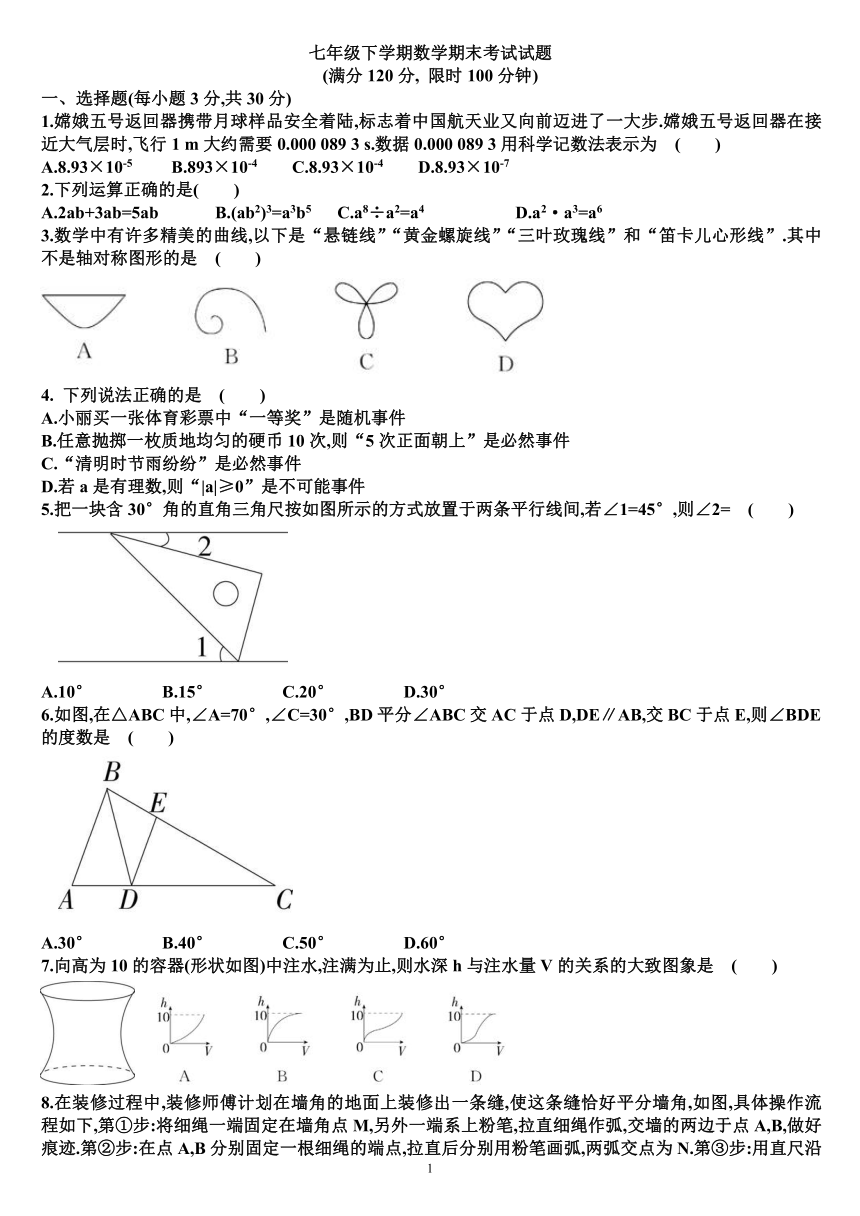 | |
| 格式 | docx | ||
| 文件大小 | 242.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 21:13:09 | ||
图片预览


文档简介
七年级下学期数学期末考试试题
(满分120分, 限时100分钟)
一、选择题(每小题3分,共30分)
1.嫦娥五号返回器携带月球样品安全着陆,标志着中国航天业又向前迈进了一大步.嫦娥五号返回器在接近大气层时,飞行1 m大约需要0.000 089 3 s.数据0.000 089 3用科学记数法表示为 ( )
A.8.93×10-5 B.893×10-4 C.8.93×10-4 D.8.93×10-7
2.下列运算正确的是( )
A.2ab+3ab=5ab B.(ab2)3=a3b5 C.a8÷a2=a4 D.a2·a3=a6
3.数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡儿心形线”.其中不是轴对称图形的是 ( )
4. 下列说法正确的是 ( )
A.小丽买一张体育彩票中“一等奖”是随机事件
B.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
C.“清明时节雨纷纷”是必然事件
D.若a是有理数,则“|a|≥0”是不可能事件
5.把一块含30°角的直角三角尺按如图所示的方式放置于两条平行线间,若∠1=45°,则∠2= ( )
A.10° B.15° C.20° D.30°
6.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
7.向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量V的关系的大致图象是 ( )
8.在装修过程中,装修师傅计划在墙角的地面上装修出一条缝,使这条缝恰好平分墙角,如图,具体操作流程如下,第①步:将细绳一端固定在墙角点M,另外一端系上粉笔,拉直细绳作弧,交墙的两边于点A,B,做好痕迹.第②步:在点A,B分别固定一根细绳的端点,拉直后分别用粉笔画弧,两弧交点为N.第③步:用直尺沿着墙角点M和弧交点N作射线MN,这条射线就是要装修的细缝.其原理是 ( )
A.边角边 B.角边角 C.角角边 D.边边边
9.近几年,二维码逐渐进入了人们的生活,成为广大民众生活中不可或缺的一部分,如图所示的是一个二维码,小莲将二维码打印在面积为20的正方形纸片上,为了估计黑色部分的面积,她在纸片内随机掷点,经过大量试验,发现点落在黑色部分的频率稳定在0.75左右,则据此估计此二维码黑色部分的面积为 ( )
A.15 B.5 C.0.75 D.0.25
10.现有甲、乙两个正方形纸片,将甲、乙并列放置后得到图1,已知点H为AE的中点,连接DH、FH,将乙放到甲的内部得到图2,已知甲、乙两个正方形边长之和为8,图2中的阴影部分面积为6,则图1中的阴影部分面积为 ( )
A.3 B.19 C.21 D.28
二、填空题(每小题3分,共18分)
11.某小区物业打算将小区内的一块空地建成周长为100米的长方形花园,若花园的宽为a米,面积为S平方米,则S关于a的关系式为 .
12.围棋起源于中国,古代称为“弈”.如图所示的是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,则所得的对弈图是轴对称图形.(填写A,B,C,D中的一处即可,A,B,C,D位于棋盘的格点上)
13.端午节是我国四大传统节日之一,吃粽子是端午节的传统习俗,端午节这天,小美的妈妈买了3只红豆粽和5只蛋黄粽,这些粽子除了内部馅料不同外其他均相同.小美从中随意选一个,她选到红豆粽的概率是 .
14.如图,长方形ABCD沿EF对折后,若∠1=50°,则∠AEF= °.
15.如图,△ACB≌△AC'B',∠ACB=90°,CC'的延长线与BB'相交于点D,∠DCB=16°,则∠B'C'D的大小为 .
16.已知2x-3y+3=0,则4x÷8y= .
三、解答题(共72分)
17.[答案含评分细则](2024河南郑州期末)(6分)
(1)计算:()0+5-2-(-1)2030.
(2)先化简,再求值:[(2x-y)(2x+y)-(x-y)2-3x2]÷(2y),其中x=1,y=2.
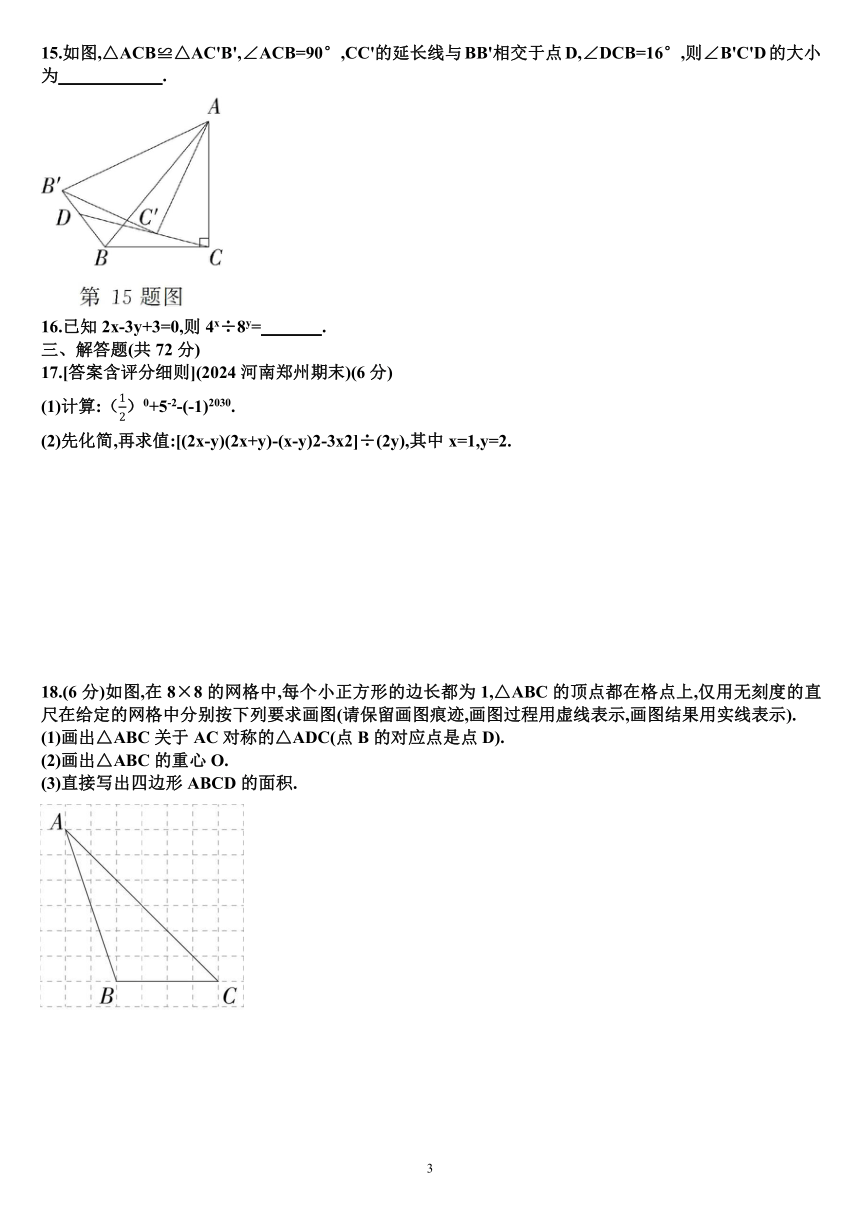
18.(6分)如图,在8×8的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示).
(1)画出△ABC关于AC对称的△ADC(点B的对应点是点D).
(2)画出△ABC的重心O.
(3)直接写出四边形ABCD的面积.
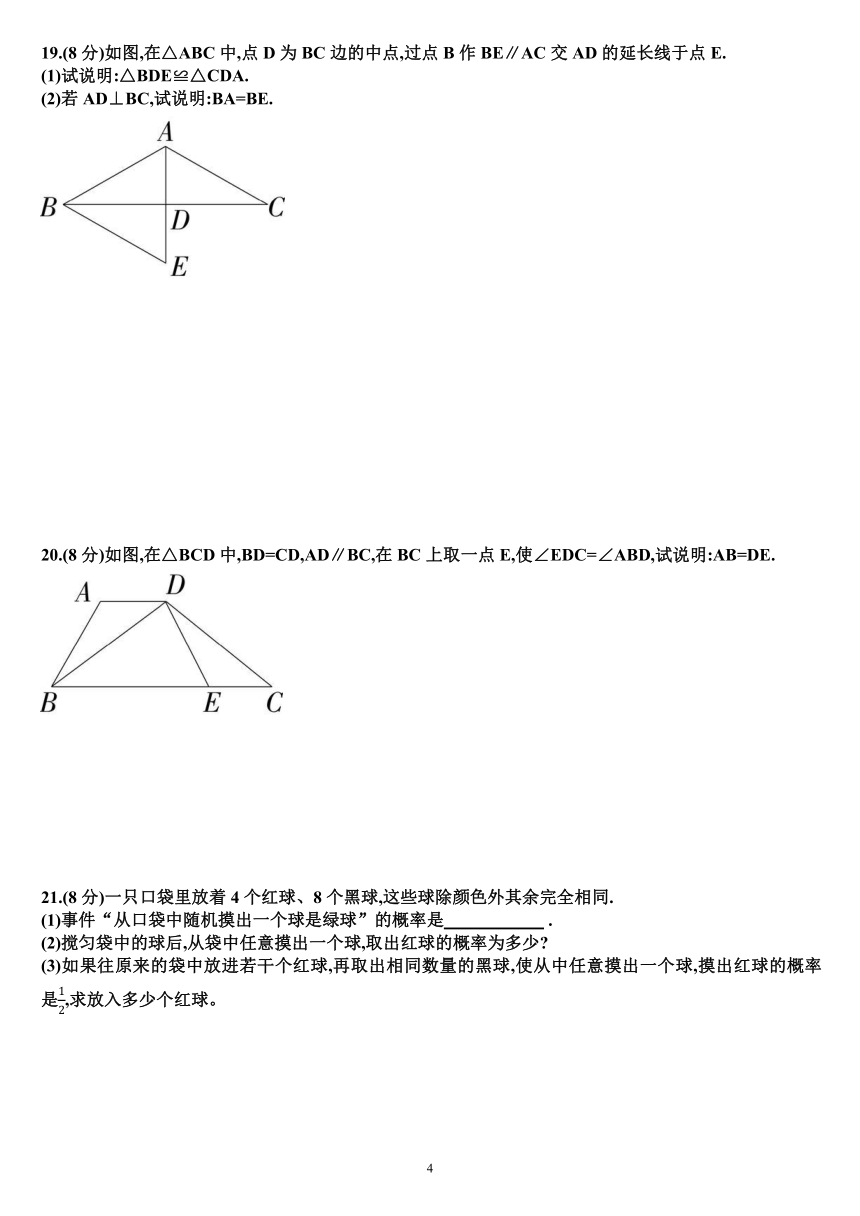
19.(8分)如图,在△ABC中,点D为BC边的中点,过点B作BE∥AC交AD的延长线于点E.
(1)试说明:△BDE≌△CDA.
(2)若AD⊥BC,试说明:BA=BE.
20.(8分)如图,在△BCD中,BD=CD,AD∥BC,在BC上取一点E,使∠EDC=∠ABD,试说明:AB=DE.
21.(8分)一只口袋里放着4个红球、8个黑球,这些球除颜色外其余完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”的概率是 .
(2)搅匀袋中的球后,从袋中任意摸出一个球,取出红球的概率为多少
(3)如果往原来的袋中放进若干个红球,再取出相同数量的黑球,使从中任意摸出一个球,摸出红球的概率是,求放入多少个红球。
22.(10分)如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
23.(12分)一条笔直的路上依次有M、P、N三地,其中M、N两地相距1 000米.甲、乙两机器人分别从M、N两地同时出发,分别去目的地N、M,匀速而行.图中OA、BC分别表示甲、乙机器人离M地的距离y(米)与行走时间x(分钟)的关系图象.
(1)求甲机器人离M地的距离y(米)与行走时间x(分钟)的关系式.
(2)出发后,甲机器人行走多长时间与乙机器人相遇
(3)甲机器人到P地后,再经过1分钟乙机器人也到P地,求P、M两地间的距离.
24.(14分)如图①,在Rt△ABC中,∠C=90°,BC=9 cm,AC=12 cm,AB=15 cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3 cm/s,设运动时间为t s.
(1)如图①,当t= 时,△APC的面积等于△ABC面积的一半.
(2)如图②,在△DEF中,∠E=90°,DE=4 cm,DF=5 cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.两点运动过程中的某一时刻,恰好有△APQ≌△DEF,求点Q的运动速度.
答案
1.A 2.A 3.B 4.A 5.B 6.B 7.D 8.D 9.A 10.B
11.S=-a2+50a 12.A 13. 14.115° 15.16° 16.
17.(1) (2)x-y. 当x=1,y=2时,原式=1-2=-1
18. (1)如图,△ADC即为所求.
(2)如图,点O即为所求.
(3)四边形ABCD的面积=2××4×6=24.
19. (1)因为点D为BC的中点,
所以BD=CD.
因为BE∥AC,
所以∠EBD=∠C,∠E=∠CAD.
所以△BDE≌△CDA(AAS).
(2)因为点D为BC的中点,AD⊥BC,
所以BA=CA.
由(1)知△BDE≌△CDA,所以BE=CA.
所以BA=BE.
20.因为BD=CD,
所以∠DBC=∠C.
因为AD∥BC,所以∠ADB=∠DBC.
所以∠C=∠ADB.
在△ABD与△EDC中,
所以△ABD≌△EDC(ASA).
所以AB=DE.
21. (1)0.
(2)从袋中任意摸出一个球有4+8=12种等可能结果,其中是红球的有4种结果,
所以从袋中任意摸出一个球是红球的概率为=.
(3)设放入x个红球,根据题意,得=,
解得x=2.
答:放入2个红球.
22.如图,过点D作DF⊥AC交CA的延长线于点F,
因为CD平分∠ACB,DE⊥BC于E,
所以DF=DE.
因为△ABC的面积为14,所以S△BCD+S△ACD=14.
所以×DE×10+×DF×4=14,即5DE+2DE=14.
所以DE=2.
23. (1)由题图可知甲机器人的速度为1 000÷5=200(米/分钟),
所以甲机器人离M地的距离y(米)与行走时间x(分钟)的关系式为y=200x.
(2)乙机器人的速度为1 000÷10=100(米/分钟),
两人相遇的时间为=(分钟).
答:出发后,甲机器人行走分钟与乙机器人相遇.
(3)设甲机器人行走t分钟到P地,则乙机器人(t+1)分钟后到P
地,根据题意,得200t=1 000-100(t+1),解得t=3.
所以200t=600.
答:P、M两地间的距离为600米.
24. (1)或.
②当点P在BA上时,如图②,
因为△APC的面积等于△ABC面积的一半,所以点P为BA的中点,此时,点P移动的路程为AC+CB+BP=12+9+=(cm),故此时点P移动的时间为÷3=(秒).
(2)因为△APQ≌△DEF,
所以对应顶点为点A与点D,点P与点E,点Q与点F,AP=DE=4 cm,AQ=DF=5 cm.
①如图③,当点P在AC上,点Q在AB上时,AP=4 cm,AQ=5 cm,
所以点Q的运动速度为5÷(4÷3)=(cm/s).
②如图④,当点P在AB上,点Q在AC上时,AP=4 cm,AQ=5 cm,
点P运动的路程为9+15+12-4=32(cm),点Q运动的路程为9+12
+15-5=31(cm),所以点Q的运动速度为31÷(32÷3)=(cm/s).
综上所述,点Q的运动速度为cm/s或cm/s.
(满分120分, 限时100分钟)
一、选择题(每小题3分,共30分)
1.嫦娥五号返回器携带月球样品安全着陆,标志着中国航天业又向前迈进了一大步.嫦娥五号返回器在接近大气层时,飞行1 m大约需要0.000 089 3 s.数据0.000 089 3用科学记数法表示为 ( )
A.8.93×10-5 B.893×10-4 C.8.93×10-4 D.8.93×10-7
2.下列运算正确的是( )
A.2ab+3ab=5ab B.(ab2)3=a3b5 C.a8÷a2=a4 D.a2·a3=a6
3.数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡儿心形线”.其中不是轴对称图形的是 ( )
4. 下列说法正确的是 ( )
A.小丽买一张体育彩票中“一等奖”是随机事件
B.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
C.“清明时节雨纷纷”是必然事件
D.若a是有理数,则“|a|≥0”是不可能事件
5.把一块含30°角的直角三角尺按如图所示的方式放置于两条平行线间,若∠1=45°,则∠2= ( )
A.10° B.15° C.20° D.30°
6.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是 ( )
A.30° B.40° C.50° D.60°
7.向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量V的关系的大致图象是 ( )
8.在装修过程中,装修师傅计划在墙角的地面上装修出一条缝,使这条缝恰好平分墙角,如图,具体操作流程如下,第①步:将细绳一端固定在墙角点M,另外一端系上粉笔,拉直细绳作弧,交墙的两边于点A,B,做好痕迹.第②步:在点A,B分别固定一根细绳的端点,拉直后分别用粉笔画弧,两弧交点为N.第③步:用直尺沿着墙角点M和弧交点N作射线MN,这条射线就是要装修的细缝.其原理是 ( )
A.边角边 B.角边角 C.角角边 D.边边边
9.近几年,二维码逐渐进入了人们的生活,成为广大民众生活中不可或缺的一部分,如图所示的是一个二维码,小莲将二维码打印在面积为20的正方形纸片上,为了估计黑色部分的面积,她在纸片内随机掷点,经过大量试验,发现点落在黑色部分的频率稳定在0.75左右,则据此估计此二维码黑色部分的面积为 ( )
A.15 B.5 C.0.75 D.0.25
10.现有甲、乙两个正方形纸片,将甲、乙并列放置后得到图1,已知点H为AE的中点,连接DH、FH,将乙放到甲的内部得到图2,已知甲、乙两个正方形边长之和为8,图2中的阴影部分面积为6,则图1中的阴影部分面积为 ( )
A.3 B.19 C.21 D.28
二、填空题(每小题3分,共18分)
11.某小区物业打算将小区内的一块空地建成周长为100米的长方形花园,若花园的宽为a米,面积为S平方米,则S关于a的关系式为 .
12.围棋起源于中国,古代称为“弈”.如图所示的是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,则所得的对弈图是轴对称图形.(填写A,B,C,D中的一处即可,A,B,C,D位于棋盘的格点上)
13.端午节是我国四大传统节日之一,吃粽子是端午节的传统习俗,端午节这天,小美的妈妈买了3只红豆粽和5只蛋黄粽,这些粽子除了内部馅料不同外其他均相同.小美从中随意选一个,她选到红豆粽的概率是 .
14.如图,长方形ABCD沿EF对折后,若∠1=50°,则∠AEF= °.
15.如图,△ACB≌△AC'B',∠ACB=90°,CC'的延长线与BB'相交于点D,∠DCB=16°,则∠B'C'D的大小为 .
16.已知2x-3y+3=0,则4x÷8y= .
三、解答题(共72分)
17.[答案含评分细则](2024河南郑州期末)(6分)
(1)计算:()0+5-2-(-1)2030.
(2)先化简,再求值:[(2x-y)(2x+y)-(x-y)2-3x2]÷(2y),其中x=1,y=2.
18.(6分)如图,在8×8的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示).
(1)画出△ABC关于AC对称的△ADC(点B的对应点是点D).
(2)画出△ABC的重心O.
(3)直接写出四边形ABCD的面积.
19.(8分)如图,在△ABC中,点D为BC边的中点,过点B作BE∥AC交AD的延长线于点E.
(1)试说明:△BDE≌△CDA.
(2)若AD⊥BC,试说明:BA=BE.
20.(8分)如图,在△BCD中,BD=CD,AD∥BC,在BC上取一点E,使∠EDC=∠ABD,试说明:AB=DE.
21.(8分)一只口袋里放着4个红球、8个黑球,这些球除颜色外其余完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”的概率是 .
(2)搅匀袋中的球后,从袋中任意摸出一个球,取出红球的概率为多少
(3)如果往原来的袋中放进若干个红球,再取出相同数量的黑球,使从中任意摸出一个球,摸出红球的概率是,求放入多少个红球。
22.(10分)如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
23.(12分)一条笔直的路上依次有M、P、N三地,其中M、N两地相距1 000米.甲、乙两机器人分别从M、N两地同时出发,分别去目的地N、M,匀速而行.图中OA、BC分别表示甲、乙机器人离M地的距离y(米)与行走时间x(分钟)的关系图象.
(1)求甲机器人离M地的距离y(米)与行走时间x(分钟)的关系式.
(2)出发后,甲机器人行走多长时间与乙机器人相遇
(3)甲机器人到P地后,再经过1分钟乙机器人也到P地,求P、M两地间的距离.
24.(14分)如图①,在Rt△ABC中,∠C=90°,BC=9 cm,AC=12 cm,AB=15 cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3 cm/s,设运动时间为t s.
(1)如图①,当t= 时,△APC的面积等于△ABC面积的一半.
(2)如图②,在△DEF中,∠E=90°,DE=4 cm,DF=5 cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.两点运动过程中的某一时刻,恰好有△APQ≌△DEF,求点Q的运动速度.
答案
1.A 2.A 3.B 4.A 5.B 6.B 7.D 8.D 9.A 10.B
11.S=-a2+50a 12.A 13. 14.115° 15.16° 16.
17.(1) (2)x-y. 当x=1,y=2时,原式=1-2=-1
18. (1)如图,△ADC即为所求.
(2)如图,点O即为所求.
(3)四边形ABCD的面积=2××4×6=24.
19. (1)因为点D为BC的中点,
所以BD=CD.
因为BE∥AC,
所以∠EBD=∠C,∠E=∠CAD.
所以△BDE≌△CDA(AAS).
(2)因为点D为BC的中点,AD⊥BC,
所以BA=CA.
由(1)知△BDE≌△CDA,所以BE=CA.
所以BA=BE.
20.因为BD=CD,
所以∠DBC=∠C.
因为AD∥BC,所以∠ADB=∠DBC.
所以∠C=∠ADB.
在△ABD与△EDC中,
所以△ABD≌△EDC(ASA).
所以AB=DE.
21. (1)0.
(2)从袋中任意摸出一个球有4+8=12种等可能结果,其中是红球的有4种结果,
所以从袋中任意摸出一个球是红球的概率为=.
(3)设放入x个红球,根据题意,得=,
解得x=2.
答:放入2个红球.
22.如图,过点D作DF⊥AC交CA的延长线于点F,
因为CD平分∠ACB,DE⊥BC于E,
所以DF=DE.
因为△ABC的面积为14,所以S△BCD+S△ACD=14.
所以×DE×10+×DF×4=14,即5DE+2DE=14.
所以DE=2.
23. (1)由题图可知甲机器人的速度为1 000÷5=200(米/分钟),
所以甲机器人离M地的距离y(米)与行走时间x(分钟)的关系式为y=200x.
(2)乙机器人的速度为1 000÷10=100(米/分钟),
两人相遇的时间为=(分钟).
答:出发后,甲机器人行走分钟与乙机器人相遇.
(3)设甲机器人行走t分钟到P地,则乙机器人(t+1)分钟后到P
地,根据题意,得200t=1 000-100(t+1),解得t=3.
所以200t=600.
答:P、M两地间的距离为600米.
24. (1)或.
②当点P在BA上时,如图②,
因为△APC的面积等于△ABC面积的一半,所以点P为BA的中点,此时,点P移动的路程为AC+CB+BP=12+9+=(cm),故此时点P移动的时间为÷3=(秒).
(2)因为△APQ≌△DEF,
所以对应顶点为点A与点D,点P与点E,点Q与点F,AP=DE=4 cm,AQ=DF=5 cm.
①如图③,当点P在AC上,点Q在AB上时,AP=4 cm,AQ=5 cm,
所以点Q的运动速度为5÷(4÷3)=(cm/s).
②如图④,当点P在AB上,点Q在AC上时,AP=4 cm,AQ=5 cm,
点P运动的路程为9+15+12-4=32(cm),点Q运动的路程为9+12
+15-5=31(cm),所以点Q的运动速度为31÷(32÷3)=(cm/s).
综上所述,点Q的运动速度为cm/s或cm/s.
同课章节目录
