江苏无锡市湖滨中学2024-2025学年高一(下)数学第1周阶段性训练模拟练习(含解析)
文档属性
| 名称 | 江苏无锡市湖滨中学2024-2025学年高一(下)数学第1周阶段性训练模拟练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 748.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 19:17:16 | ||
图片预览



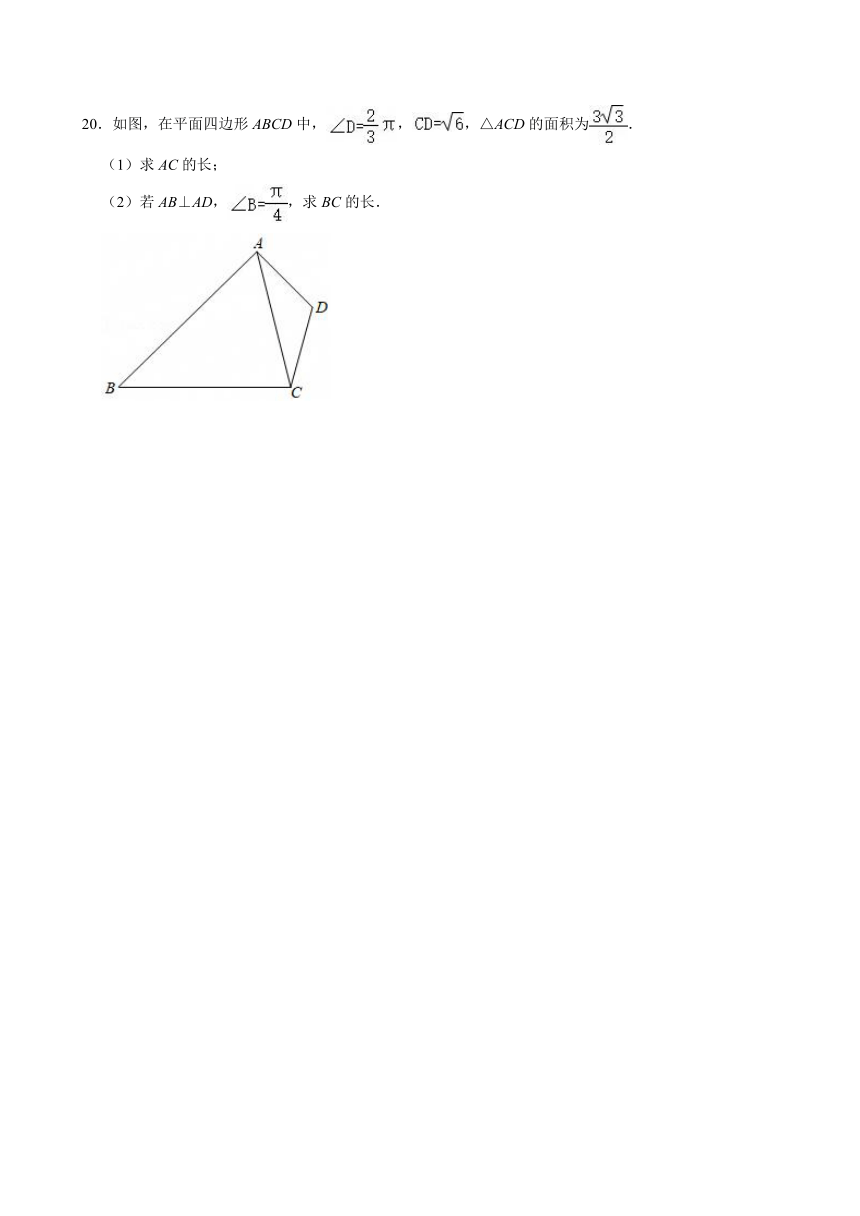

文档简介
江苏无锡市湖滨中学2024-2025学年高一(下)数学第1周阶段性训练模拟练习
一.选择题(共11小题)
1.已知sin(30°+α)=,60°<α<150°,则cosα=( )
A. B. C. D.
2.在△ABC中,角A,B,C的对边分别是边a,b,c,若a=3,c=2,A+C=,则b=( )
A. B.6 C.7 D.8
3.在△ABC中,若=,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
4.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若,b2+c2﹣bc=3,则△ABC面积的取值范围是( )
A. B.
C. D.
5.已知α∈(0,π),若,则=( )
A. B. C. D.
6.函数f(x)=cos2x+6sinx+1的值域是( )
A. B. C. D.[﹣6,6]
7.在△ABC中,∠A=30°,BC=4,满足此条件的△ABC有两解,则AB的取值范围为( )
A.(2,4) B.(2,8) C.(4,8) D.(4,+∞)
8.已知△ABC的内角A,B,C所对的边分别是a,b,c,若a=1,A=135°,则的值为( )
A. B. C. D.
9.设tanα、tanβ是方程x2﹣3x+2=0的两个根,则tan(α+β)=( )
A.﹣3 B.3 C.﹣1 D.1
10.在△ABC,其内角A,B,C的对边分别为a,b,c,若acosB+bcosA=a,则△ABC的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
11.在△ABC中,a=x厘米,b=2厘米,B=45°.若利用正弦定理解△ABC有两解,则x的取值范围是( )
A. B. C.x>2 D.
二.多选题(共4小题)
(多选)12.下列各式中,值为的有( )
A.sin7°cos23°+sin83°cos67°
B.
C.
D.
(多选)13.△ABC中,角A,B,C所对的边分别为a,b,c,且c﹣b=2bcsA,则下列结论正确的有( )
A.A=2B
B.若,则△ABC为直角三角形
C.若△ABC为锐角三角形,的最小值为1
D.若△ABC为锐角三角形,则的取值范围为
(多选)14.已知角A,B,C是斜三角形ABC的三个内角,下列结论一定成立的有( )
A.sin(A+B)=sinC
B.
C.若sinA>sinB,则A>B
D.tanA+tanB+tanC=tanAtanBtanC
(多选)15.已知△ABC的内角A,B,C所对的边分别为a,b,c,则下列命题正确的是( )
A.若asinA=bsinB,则△ABC一定为等腰三角形
B.若A>B,则cosA>cosB
C.若a:b:c=3:5:7,则△ABC的最大内角为120°
D.若△ABC为锐角三角形,则sinA>cosB
三.填空题(共2小题)
16.化简:= .
17.f(x)=sinxcosxcos2x的最大值为 .
四.解答题(共3小题)
18.在△ABC中,角A,B,C的对边分别是a,b,c,且.
(1)求角B的大小;
(2)若,△ABC的面积为,求△ABC的周长;
(3)若,D为AC边上的一点,BD=3,且_____,求△ABC的面积.
(从下面①,②两个条件中任选一个,补充在上面的横线上并作答).
①BD是∠B的平分线;
②D为线段AC的中点.
19.在直角三角形ABC中,B=90°,点E,F在边BC上,且BE=EF=FC,设BA=c,BC=a.
(1)若a=c,求tan∠EAF,tan∠FAC的值;
(2)若a=3,求tan∠EAF的最大值.
20.如图,在平面四边形ABCD中,,,△ACD的面积为.
(1)求AC的长;
(2)若AB⊥AD,,求BC的长.
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A A D A D D A C A A B
一.选择题(共11小题)
1.【解答】解:∵60°<α<150°,∴90°<α+30°<180°,
∵sin(30°+α)=,
∴cos(30°+α)=﹣=﹣,
则cosα=cos[(30°+α)﹣30°]=cos(30°+α)cos30°+sin(30°+α)sin30°=﹣×+×=.
故选:A.
2.【解答】解:∵A+C=,
∴B=π﹣(A+C)=,
∵a=3,c=2,
∴由余弦定理可得:b===.
故选:A.
3.【解答】解:∵cosB=,cosA=,
∴a2+c2﹣b2=2ac cosB,b2+c2﹣a2=2bc cosA,
∴===,又=,
∴==,即sinAcosA=sinBcosB,
∴sin2A=sin2B,又A和B都为三角形的内角,
∴2A=2B或2A+2B=180°,即A=B或A+B=90°,
则△ABC为等腰三角形或直角三角形.
故选:D.
4.【解答】解:由于a=,b2+c2﹣bc=3,
则,
由于A∈(0,π),
所以A=,
故外接圆的半径为R=,
所以=
=
=
=,
由于,
由于△ABC为锐角三角形,
所以,
所以,
故,即.
故选:A.
5.【解答】解:∵α∈(0,π),,
∴sinα==,
∴=sinαcos﹣cosαsin=×﹣(﹣)×=.
故选:D.
6.【解答】解:f(x)=cos2x+6sinx+1=1﹣2sin2x+6sinx+1=﹣2sin2x+6sinx+2=,
由于﹣1≤sinx≤1,
故f(x)∈[﹣6,6].
故选:D.
7.【解答】解:∵△ABC有两解,
∴BCsin30°<AB<BC,∴2<AB<4.
故选:A.
8.【解答】解:因为a=1,A=135°,
由正弦定理===,可得b=sinB,c=sinC,
则==.
故选:C.
9.【解答】解:∵tanα,tanβ是方程x2﹣3x+2=0的两个根,
∴tanα+tanβ=3,tanαtanβ=2,
则tan(α+β)===﹣3.
故选:A.
10.【解答】解:∵a=acosB+bcosA,
∴由余弦定理可得:a=a×+b×,整理可得:2ac=2c2,
∴a=c,则△ABC的形状为等腰三角形.
故选:A.
11.【解答】解:如图,
B=45°,CD⊥AB,则CD=BC sin45°=asin45°=xsin45°,
以C为圆心,CA=b=2为半径画圆弧,要使△ABC有两个解,则圆弧和BA边应该有两个交点,
故CA>CD且CA<CB,即xsin45°<2<x,
解得.
故选:B.
二.多选题(共4小题)
12.【解答】解:对于A,sin7°cos23°+sin83°cos67°=sin7°cos23°+cos7°sin23°=sin(7°+23°)=sin30°=;
对于B,+====4;
对于C,=tan(2×22.5°)=;
对于D,=
=
=.
故选:ACD.
13.【解答】解:选项A中,因为c﹣b=2bcsA,由正弦定理可得sinC=sinB(2cosA+1),
在△ABC中,sinC=sin(A+B)=sinAcosB+cosAsinB,
可得sin(A﹣B)=sinB,所以A﹣B=B或A﹣B+B=π(舍去),
即A=2B,故A正确;
选项B中,a=b,可得sinA=sinB,由A选项可得sin2B=sinB,
则2sinBcosB=sinB,在△ABC中,sinB>0,
可得cosB=,则B=,A=,所以C=,即△ABC为直角三角形,故B正确;
选项C中,因为△ABC为锐角三角形,由A选项可得A=2B,
所以,可得<B<,所以tanB∈(,1),
所以﹣=﹣=+,
设s=tanB∈(,1),又g(s)=+在(,1)单调递减,
所以g(s)>g(1)=1,故C错误;
选项D中,△ABC为锐角三角形,
=====cosB+=2cosB﹣,
因为△ABC为锐角三角形,所以,可得<B<,
所以cosB∈(,),设t=cosB,即t∈(,),
令f(t)=2t﹣,t∈(,),
则函数f(t)单调递增,f()<f(t)<f(),
而f()=﹣=,f()=﹣=,
所以f(t)∈(,),即∈(,),故D正确.
故选:ABD.
14.【解答】解:在△ABC中,有A+B+C=π,
sin(A+B)=sin(π﹣C)=sinC,故A正确;
=sin=cosC,B错误;
由正弦定理得sinA>sinB a>b A>B,故C正确;
斜△ABC中,A+B=π﹣C,
∴tan(A+B)=tan(π﹣C)=﹣tanC,
又tan(A+B)=,
∴=﹣tanC,
整理得:tanA+tanB+tanC=tanAtanBtanC,故D正确.
故选:ACD.
15.【解答】解:对于A,由asinA=bsinB和正弦定理得:a2=b2,∴a=b.故A正确;
对于B,由0<B<A<π及余弦函数在(0,π)单调递减,得cosA<cosB,故B错误;
对于C,由a:b:c=3:5:7及大边对大角得,角C最大,设a=3k,b=5k,c=7k(k>0),
则,∵C∈(0,π)∴c=120°,故C正确;
对于D,由△ABC为锐角三角形得A+B,∴,又正弦函数在单调递增,
∴,即sinA>cosB,故D正确.
故选:ACD.
三.填空题(共2小题)
16.【解答】解:===tan15°
=tan(45°﹣30°)===2﹣,
故答案为:2﹣.
17.【解答】解:f(x)=sinxcosxcos2x=sin2xcos2x=sin4x≤,
即函数的最大值为,当sin4x=1,即x=+,k∈Z时取等号.
故答案为:.
四.解答题(共3小题)
18.【解答】解:(1)在△ABC中,,
结合正弦定理可得; ,
由A∈(0,π),可得sinA>0,
则有2sinC=sinA+2sinBcosA,
即2sin(A+B)=sin A+2sin BcosA,
化简得2sinAcosB=sinA,即,
又B∈(0,π),所以;
(2)由,得ac=8,
由余弦定理,得,即a2+c2﹣8=ac,
即(a+c)2=3ac+8=32,解得,
所以△ABC的周长为;
(3)若选①:由BD平分∠ABC,得S△ABC=S△ABD+S△BCD,
可得,即,③
在△ABC中,由余弦定理,得,则a2+c2﹣ac=12,④
联立③④,可得(ac)2﹣9ac=36,解得ac=12,
故;
若选②:由题设,
则,
所以a2+c2+ac=36,⑤
在△ABC中,由余弦定理得,则a2+c2﹣ac=12,⑥
联立⑤⑥,可得ac=12,
故.
19.【解答】解:(1)若a=c,
则三角形ABC为等腰直角三角形,
所以∠BAC=45°,tan ,tan,
所以tan∠EAF=tan(∠BAF﹣∠BAE)==,
;
(2)若a=3,
则,,
所以tan∠EAF=tan(∠BAF﹣∠BAE)=== =,当且仅当时取等号,
所以tanEAF的最大值为.
20.【解答】解:(1)∵,,△ACD的面积为,
∴=,
∴,
∴由余弦定理,得AC2=AD2+CD2﹣2AD CD cosD
=,
∴;
(2)由(1)知△ACD中,,,
∴,∵AB⊥AD,∴,
又∵,,
∴在△ABC中,由正弦定理,得,
即,∴.
一.选择题(共11小题)
1.已知sin(30°+α)=,60°<α<150°,则cosα=( )
A. B. C. D.
2.在△ABC中,角A,B,C的对边分别是边a,b,c,若a=3,c=2,A+C=,则b=( )
A. B.6 C.7 D.8
3.在△ABC中,若=,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
4.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若,b2+c2﹣bc=3,则△ABC面积的取值范围是( )
A. B.
C. D.
5.已知α∈(0,π),若,则=( )
A. B. C. D.
6.函数f(x)=cos2x+6sinx+1的值域是( )
A. B. C. D.[﹣6,6]
7.在△ABC中,∠A=30°,BC=4,满足此条件的△ABC有两解,则AB的取值范围为( )
A.(2,4) B.(2,8) C.(4,8) D.(4,+∞)
8.已知△ABC的内角A,B,C所对的边分别是a,b,c,若a=1,A=135°,则的值为( )
A. B. C. D.
9.设tanα、tanβ是方程x2﹣3x+2=0的两个根,则tan(α+β)=( )
A.﹣3 B.3 C.﹣1 D.1
10.在△ABC,其内角A,B,C的对边分别为a,b,c,若acosB+bcosA=a,则△ABC的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰或直角三角形
11.在△ABC中,a=x厘米,b=2厘米,B=45°.若利用正弦定理解△ABC有两解,则x的取值范围是( )
A. B. C.x>2 D.
二.多选题(共4小题)
(多选)12.下列各式中,值为的有( )
A.sin7°cos23°+sin83°cos67°
B.
C.
D.
(多选)13.△ABC中,角A,B,C所对的边分别为a,b,c,且c﹣b=2bcsA,则下列结论正确的有( )
A.A=2B
B.若,则△ABC为直角三角形
C.若△ABC为锐角三角形,的最小值为1
D.若△ABC为锐角三角形,则的取值范围为
(多选)14.已知角A,B,C是斜三角形ABC的三个内角,下列结论一定成立的有( )
A.sin(A+B)=sinC
B.
C.若sinA>sinB,则A>B
D.tanA+tanB+tanC=tanAtanBtanC
(多选)15.已知△ABC的内角A,B,C所对的边分别为a,b,c,则下列命题正确的是( )
A.若asinA=bsinB,则△ABC一定为等腰三角形
B.若A>B,则cosA>cosB
C.若a:b:c=3:5:7,则△ABC的最大内角为120°
D.若△ABC为锐角三角形,则sinA>cosB
三.填空题(共2小题)
16.化简:= .
17.f(x)=sinxcosxcos2x的最大值为 .
四.解答题(共3小题)
18.在△ABC中,角A,B,C的对边分别是a,b,c,且.
(1)求角B的大小;
(2)若,△ABC的面积为,求△ABC的周长;
(3)若,D为AC边上的一点,BD=3,且_____,求△ABC的面积.
(从下面①,②两个条件中任选一个,补充在上面的横线上并作答).
①BD是∠B的平分线;
②D为线段AC的中点.
19.在直角三角形ABC中,B=90°,点E,F在边BC上,且BE=EF=FC,设BA=c,BC=a.
(1)若a=c,求tan∠EAF,tan∠FAC的值;
(2)若a=3,求tan∠EAF的最大值.
20.如图,在平面四边形ABCD中,,,△ACD的面积为.
(1)求AC的长;
(2)若AB⊥AD,,求BC的长.
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A A D A D D A C A A B
一.选择题(共11小题)
1.【解答】解:∵60°<α<150°,∴90°<α+30°<180°,
∵sin(30°+α)=,
∴cos(30°+α)=﹣=﹣,
则cosα=cos[(30°+α)﹣30°]=cos(30°+α)cos30°+sin(30°+α)sin30°=﹣×+×=.
故选:A.
2.【解答】解:∵A+C=,
∴B=π﹣(A+C)=,
∵a=3,c=2,
∴由余弦定理可得:b===.
故选:A.
3.【解答】解:∵cosB=,cosA=,
∴a2+c2﹣b2=2ac cosB,b2+c2﹣a2=2bc cosA,
∴===,又=,
∴==,即sinAcosA=sinBcosB,
∴sin2A=sin2B,又A和B都为三角形的内角,
∴2A=2B或2A+2B=180°,即A=B或A+B=90°,
则△ABC为等腰三角形或直角三角形.
故选:D.
4.【解答】解:由于a=,b2+c2﹣bc=3,
则,
由于A∈(0,π),
所以A=,
故外接圆的半径为R=,
所以=
=
=
=,
由于,
由于△ABC为锐角三角形,
所以,
所以,
故,即.
故选:A.
5.【解答】解:∵α∈(0,π),,
∴sinα==,
∴=sinαcos﹣cosαsin=×﹣(﹣)×=.
故选:D.
6.【解答】解:f(x)=cos2x+6sinx+1=1﹣2sin2x+6sinx+1=﹣2sin2x+6sinx+2=,
由于﹣1≤sinx≤1,
故f(x)∈[﹣6,6].
故选:D.
7.【解答】解:∵△ABC有两解,
∴BCsin30°<AB<BC,∴2<AB<4.
故选:A.
8.【解答】解:因为a=1,A=135°,
由正弦定理===,可得b=sinB,c=sinC,
则==.
故选:C.
9.【解答】解:∵tanα,tanβ是方程x2﹣3x+2=0的两个根,
∴tanα+tanβ=3,tanαtanβ=2,
则tan(α+β)===﹣3.
故选:A.
10.【解答】解:∵a=acosB+bcosA,
∴由余弦定理可得:a=a×+b×,整理可得:2ac=2c2,
∴a=c,则△ABC的形状为等腰三角形.
故选:A.
11.【解答】解:如图,
B=45°,CD⊥AB,则CD=BC sin45°=asin45°=xsin45°,
以C为圆心,CA=b=2为半径画圆弧,要使△ABC有两个解,则圆弧和BA边应该有两个交点,
故CA>CD且CA<CB,即xsin45°<2<x,
解得.
故选:B.
二.多选题(共4小题)
12.【解答】解:对于A,sin7°cos23°+sin83°cos67°=sin7°cos23°+cos7°sin23°=sin(7°+23°)=sin30°=;
对于B,+====4;
对于C,=tan(2×22.5°)=;
对于D,=
=
=.
故选:ACD.
13.【解答】解:选项A中,因为c﹣b=2bcsA,由正弦定理可得sinC=sinB(2cosA+1),
在△ABC中,sinC=sin(A+B)=sinAcosB+cosAsinB,
可得sin(A﹣B)=sinB,所以A﹣B=B或A﹣B+B=π(舍去),
即A=2B,故A正确;
选项B中,a=b,可得sinA=sinB,由A选项可得sin2B=sinB,
则2sinBcosB=sinB,在△ABC中,sinB>0,
可得cosB=,则B=,A=,所以C=,即△ABC为直角三角形,故B正确;
选项C中,因为△ABC为锐角三角形,由A选项可得A=2B,
所以,可得<B<,所以tanB∈(,1),
所以﹣=﹣=+,
设s=tanB∈(,1),又g(s)=+在(,1)单调递减,
所以g(s)>g(1)=1,故C错误;
选项D中,△ABC为锐角三角形,
=====cosB+=2cosB﹣,
因为△ABC为锐角三角形,所以,可得<B<,
所以cosB∈(,),设t=cosB,即t∈(,),
令f(t)=2t﹣,t∈(,),
则函数f(t)单调递增,f()<f(t)<f(),
而f()=﹣=,f()=﹣=,
所以f(t)∈(,),即∈(,),故D正确.
故选:ABD.
14.【解答】解:在△ABC中,有A+B+C=π,
sin(A+B)=sin(π﹣C)=sinC,故A正确;
=sin=cosC,B错误;
由正弦定理得sinA>sinB a>b A>B,故C正确;
斜△ABC中,A+B=π﹣C,
∴tan(A+B)=tan(π﹣C)=﹣tanC,
又tan(A+B)=,
∴=﹣tanC,
整理得:tanA+tanB+tanC=tanAtanBtanC,故D正确.
故选:ACD.
15.【解答】解:对于A,由asinA=bsinB和正弦定理得:a2=b2,∴a=b.故A正确;
对于B,由0<B<A<π及余弦函数在(0,π)单调递减,得cosA<cosB,故B错误;
对于C,由a:b:c=3:5:7及大边对大角得,角C最大,设a=3k,b=5k,c=7k(k>0),
则,∵C∈(0,π)∴c=120°,故C正确;
对于D,由△ABC为锐角三角形得A+B,∴,又正弦函数在单调递增,
∴,即sinA>cosB,故D正确.
故选:ACD.
三.填空题(共2小题)
16.【解答】解:===tan15°
=tan(45°﹣30°)===2﹣,
故答案为:2﹣.
17.【解答】解:f(x)=sinxcosxcos2x=sin2xcos2x=sin4x≤,
即函数的最大值为,当sin4x=1,即x=+,k∈Z时取等号.
故答案为:.
四.解答题(共3小题)
18.【解答】解:(1)在△ABC中,,
结合正弦定理可得; ,
由A∈(0,π),可得sinA>0,
则有2sinC=sinA+2sinBcosA,
即2sin(A+B)=sin A+2sin BcosA,
化简得2sinAcosB=sinA,即,
又B∈(0,π),所以;
(2)由,得ac=8,
由余弦定理,得,即a2+c2﹣8=ac,
即(a+c)2=3ac+8=32,解得,
所以△ABC的周长为;
(3)若选①:由BD平分∠ABC,得S△ABC=S△ABD+S△BCD,
可得,即,③
在△ABC中,由余弦定理,得,则a2+c2﹣ac=12,④
联立③④,可得(ac)2﹣9ac=36,解得ac=12,
故;
若选②:由题设,
则,
所以a2+c2+ac=36,⑤
在△ABC中,由余弦定理得,则a2+c2﹣ac=12,⑥
联立⑤⑥,可得ac=12,
故.
19.【解答】解:(1)若a=c,
则三角形ABC为等腰直角三角形,
所以∠BAC=45°,tan ,tan,
所以tan∠EAF=tan(∠BAF﹣∠BAE)==,
;
(2)若a=3,
则,,
所以tan∠EAF=tan(∠BAF﹣∠BAE)=== =,当且仅当时取等号,
所以tanEAF的最大值为.
20.【解答】解:(1)∵,,△ACD的面积为,
∴=,
∴,
∴由余弦定理,得AC2=AD2+CD2﹣2AD CD cosD
=,
∴;
(2)由(1)知△ACD中,,,
∴,∵AB⊥AD,∴,
又∵,,
∴在△ABC中,由正弦定理,得,
即,∴.
同课章节目录
