9.4中心对称 同步练习 (含简略答案) 2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.4中心对称 同步练习 (含简略答案) 2024-2025学年数学华东师大版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 643.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 22:32:31 | ||
图片预览


文档简介
9.4 中心对称
1.中心对称
中心对称:把一个图形绕着某一点旋转 ,如果它能够与另一个图形 ,那么,我们就说这两个图形成 ,这个点叫做 ,这两个图形中的对应点叫做关于中心的对称点.
中心对称图形:把一个图形绕着中心 后能与 ,像这样的图形叫做 ,这个中心叫做 .
2.中心对称的性质
性质1:在成中心对称的两个图形中,连结对称点的线段都经过 ,并且被 平分.
性质2:如果两个图形的所有对应点连成的线段都经过 ,并且都被该点 ,那么这两个图形关于这一点成中心对称.
类型之一 中心对称图形的识别
下列图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
类型之二 成中心对称的性质
如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A'是对称点
B.BO=B'O
C.AB∥A'B'
D.∠ACB=∠C'A'B'
类型之三 中心对称图形的作图
如图,已知四边形ABCD和BC边的中点O.求作:四边形A'B'C'D',使它与四边形ABCD关于点O成中心对称.
1.[2024·内江]2024年6月5日是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是( )
A B C D
2.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是点 ,点A的对称点是点 ,点E的对称点是点 ;BD∥且BD= ;连结A、F的线段经过点 ,且被点C .
1.[2024·淄博]下列图案中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列说法中,正确的是( )
A.在成中心对称的图形中,连结对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连结对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点,那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
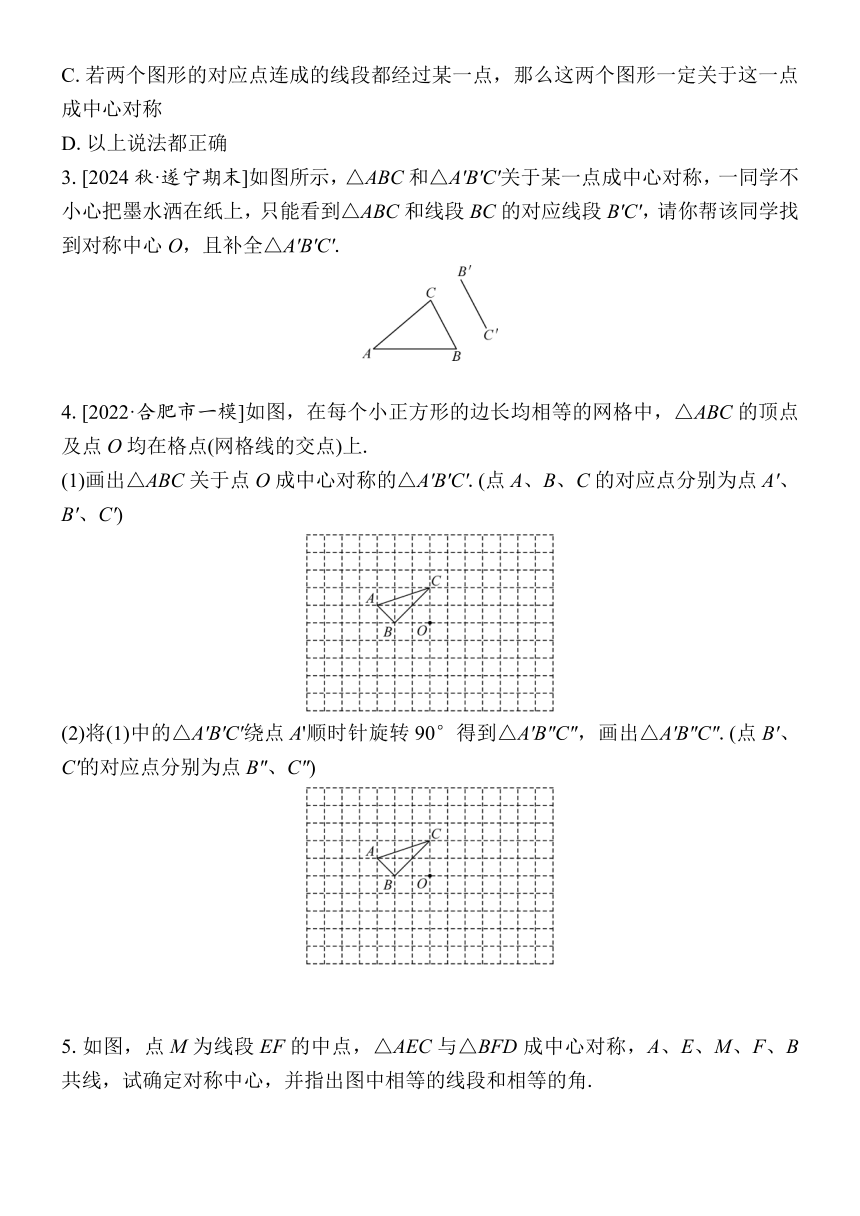
3.[2024秋·遂宁期末]如图所示,△ABC和△A'B'C'关于某一点成中心对称,一同学不小心把墨水洒在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
4.[2022·合肥市一模]如图,在每个小正方形的边长均相等的网格中,△ABC的顶点及点O均在格点(网格线的交点)上.
(1)画出△ABC关于点O成中心对称的△A'B'C'.(点A、B、C的对应点分别为点A'、B'、C')
(2)将(1)中的△A'B'C'绕点A'顺时针旋转90°得到△A'B″C″,画出△A'B″C″.(点B'、C'的对应点分别为点B″、C″)
5.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,A、E、M、F、B共线,试确定对称中心,并指出图中相等的线段和相等的角.
6.如图,在△ABC中,∠ACB=90°,△ABC旋转后能与△DEC重合,且点B、C、E三点在同一直线上.
(1)图中旋转中心是哪一点?
(2)旋转角的度数是多少?
(3)DE和AB有怎样的位置关系?
7.如图,在△ABC中,AD是BC边上的中线,△A'BD与△ACD关于点D成中心对称.
(1)直接写出图中所有相等的线段;
(2)若AB=5,AC=3,求线段AD长度的取值范围.
8.(创新意识)[2024春·保定期末]已知过中心对称图形的对称中心的任意一条直线都将其分成面积相等的两个部分.
(1)如图1,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC;(填“>”“<”或“=”)
图1
(2)如图2,两个正方形按如图所示的方式摆放,O为小正方形对角线的交点,求作一条过点O的直线使整个图形被分成两个面积相等的部分;
图2
(3)如图3,八个大小相同的正方形按如图所示的方式摆放,求作一条直线使整个图形被分成两个面积相等的部分.(用三种不同的方法分割)
图3
参考答案
【预习导航】
1.180° 重合 中心对称 对称中心
旋转180° 自身重合 中心对称图形 对称中心 2.对称中心 对称中心 某一点 平分
【归类探究】
【例1】D
【例2】D
【例3】略
【当堂测评】
1.D 2.C F D EG EG C 平分
【分层训练】
1.C 2.B 3.略 4.略
5.旋转中心为点M.
相等的线段为AC=BD,CE=DF,AE=BF,EM=FM,AM=BM,AF=BE,
相等的角为∠A=∠B,∠C=∠D,∠CEA=∠DFB,∠CEF=∠DFE.
6.(1)旋转中心是点C.
(2)旋转角的度数是180°.
(3)DE和AB的位置关系是平行.
7.(1)BD=CD,AD=A'D,AC=A'B.
(2)1<AD<4
8.(1)= (2)略 (3)略
。
1.中心对称
中心对称:把一个图形绕着某一点旋转 ,如果它能够与另一个图形 ,那么,我们就说这两个图形成 ,这个点叫做 ,这两个图形中的对应点叫做关于中心的对称点.
中心对称图形:把一个图形绕着中心 后能与 ,像这样的图形叫做 ,这个中心叫做 .
2.中心对称的性质
性质1:在成中心对称的两个图形中,连结对称点的线段都经过 ,并且被 平分.
性质2:如果两个图形的所有对应点连成的线段都经过 ,并且都被该点 ,那么这两个图形关于这一点成中心对称.
类型之一 中心对称图形的识别
下列图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
类型之二 成中心对称的性质
如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A'是对称点
B.BO=B'O
C.AB∥A'B'
D.∠ACB=∠C'A'B'
类型之三 中心对称图形的作图
如图,已知四边形ABCD和BC边的中点O.求作:四边形A'B'C'D',使它与四边形ABCD关于点O成中心对称.
1.[2024·内江]2024年6月5日是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是( )
A B C D
2.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是点 ,点A的对称点是点 ,点E的对称点是点 ;BD∥且BD= ;连结A、F的线段经过点 ,且被点C .
1.[2024·淄博]下列图案中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列说法中,正确的是( )
A.在成中心对称的图形中,连结对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连结对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点,那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
3.[2024秋·遂宁期末]如图所示,△ABC和△A'B'C'关于某一点成中心对称,一同学不小心把墨水洒在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
4.[2022·合肥市一模]如图,在每个小正方形的边长均相等的网格中,△ABC的顶点及点O均在格点(网格线的交点)上.
(1)画出△ABC关于点O成中心对称的△A'B'C'.(点A、B、C的对应点分别为点A'、B'、C')
(2)将(1)中的△A'B'C'绕点A'顺时针旋转90°得到△A'B″C″,画出△A'B″C″.(点B'、C'的对应点分别为点B″、C″)
5.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,A、E、M、F、B共线,试确定对称中心,并指出图中相等的线段和相等的角.
6.如图,在△ABC中,∠ACB=90°,△ABC旋转后能与△DEC重合,且点B、C、E三点在同一直线上.
(1)图中旋转中心是哪一点?
(2)旋转角的度数是多少?
(3)DE和AB有怎样的位置关系?
7.如图,在△ABC中,AD是BC边上的中线,△A'BD与△ACD关于点D成中心对称.
(1)直接写出图中所有相等的线段;
(2)若AB=5,AC=3,求线段AD长度的取值范围.
8.(创新意识)[2024春·保定期末]已知过中心对称图形的对称中心的任意一条直线都将其分成面积相等的两个部分.
(1)如图1,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC;(填“>”“<”或“=”)
图1
(2)如图2,两个正方形按如图所示的方式摆放,O为小正方形对角线的交点,求作一条过点O的直线使整个图形被分成两个面积相等的部分;
图2
(3)如图3,八个大小相同的正方形按如图所示的方式摆放,求作一条直线使整个图形被分成两个面积相等的部分.(用三种不同的方法分割)
图3
参考答案
【预习导航】
1.180° 重合 中心对称 对称中心
旋转180° 自身重合 中心对称图形 对称中心 2.对称中心 对称中心 某一点 平分
【归类探究】
【例1】D
【例2】D
【例3】略
【当堂测评】
1.D 2.C F D EG EG C 平分
【分层训练】
1.C 2.B 3.略 4.略
5.旋转中心为点M.
相等的线段为AC=BD,CE=DF,AE=BF,EM=FM,AM=BM,AF=BE,
相等的角为∠A=∠B,∠C=∠D,∠CEA=∠DFB,∠CEF=∠DFE.
6.(1)旋转中心是点C.
(2)旋转角的度数是180°.
(3)DE和AB的位置关系是平行.
7.(1)BD=CD,AD=A'D,AC=A'B.
(2)1<AD<4
8.(1)= (2)略 (3)略
。
