9.5图形的全等 同步练习 (含简单答案) 2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 9.5图形的全等 同步练习 (含简单答案) 2024-2025学年数学华东师大版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 531.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 00:00:00 | ||
图片预览


文档简介
9.5 图形的全等
1.全等图形
全等图形:能够 的两个图形叫做全等图形.全等用符号“ ”表示,读作“全等于”.
全等多边形:能够完全重合的两个 叫做全等多边形.相互重合的顶点叫做 ,相互重合的边叫做 ,相互重合的角叫做 .
注 意:(1)一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;
(2)两个全等图形经过上述变换后一定能够互相重合.
2.全等多边形的性质和判定
性 质:全等多边形的对应边 ,对应角 .
判 定: 的两个多边形全等.
3.全等三角形的性质和判定
性 质:全等三角形的对应边、对应角分别 .
判 定:如果两个三角形的 ,那么这两个三角形全等.
类型之一 全等多边形的性质
如图,四边形ABCD与四边形 A'B'C'D' 全等,则∠A= °,∠B= °,B'C'= ,AD= .
类型之二 全等三角形的性质
[2022春·宝安区期中]如图,已知△ABE≌△DCF,且B、F、E、C在同一条直线上.
(1)试说明AB∥CD;
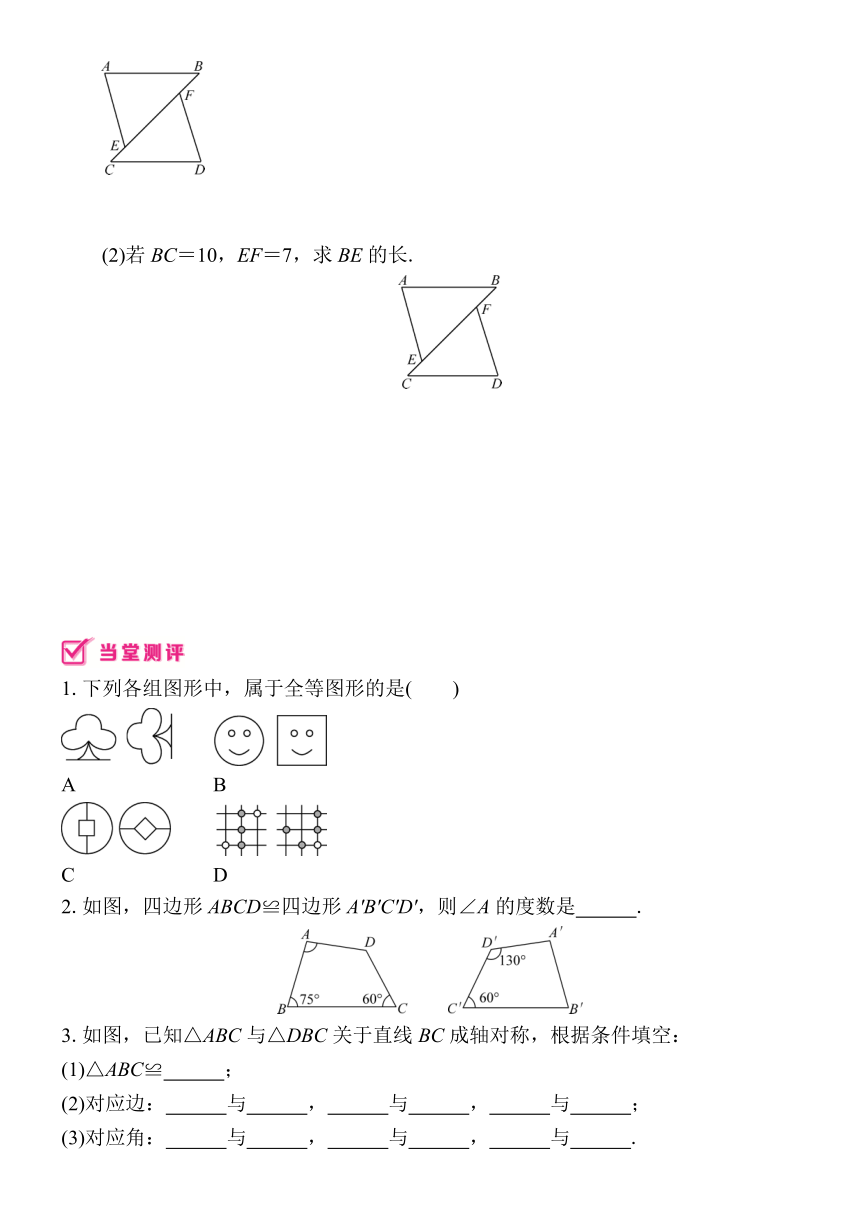
(2)若BC=10,EF=7,求BE的长.
1.下列各组图形中,属于全等图形的是( )
A B
C D
2.如图,四边形ABCD≌四边形A'B'C'D',则∠A的度数是 .
3.如图,已知△ABC与△DBC关于直线BC成轴对称,根据条件填空:
(1)△ABC≌ ;
(2)对应边: 与 , 与 , 与 ;
(3)对应角: 与 , 与 , 与 .
1.下列四个图形中,有两个全等的图形,它们是( )
① ② ③ ④
A.①和② B.②和③
C.②和④ D.③和④
2.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中不一定正确的是( )
A.BE=EC B.BC=EF
C.AC=DF D.△ABC≌△DEF
3.如图,已知△ABC≌△BAD.若∠DAC=20°,∠C=88°,则∠DBA= °.
4.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE= °,EC= .
5.[2022秋·涟水县期中]如图,△ABC≌△DEF,点B、E、C、F在同一条直线上.
(1)若∠BED=140°,∠D=75°,求∠ACB的度数;
(2)若BE=2,EC=3,求BF的长.
6.[2022秋·湖州市长兴县月考]如图,已知△ABC≌△EBD.
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
7.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长;
(2)求∠DBC的度数.
8.(推理能力)如图1,已知△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,C为AD的中点.
(1)求∠BAE的度数和AE的长;
图1
(2)如图2,延长BC,交ED于点F,求∠DFC的度数.
图2
参考答案
【预习导航】
1.完全重合 ≌ 多边形 对应顶点 对应边 对应角 2.相等 相等 边、角分别对应相等
3.相等 边、角分别相等
【归类探究】
【例1】70 85 12 6
【例2】(1)略 (2)BE=8.5
【当堂测评】
1.A 2.95° 3.(1)△DBC (2)AB DB AC DC BC BC (3)∠A ∠D ∠ABC ∠DBC ∠ACB ∠DCB
【分层训练】
1.B 2.A 3.36 4.100 2
5.(1)∠ACB=65° (2)BF=7
6.(1)AD=2 (2)∠ACE=78°
7.(1)AE=6 (2)∠DBC=10°
8.(1)∠BAE=60°,AE=2cm.
(2)∠DFC=150°
。
1.全等图形
全等图形:能够 的两个图形叫做全等图形.全等用符号“ ”表示,读作“全等于”.
全等多边形:能够完全重合的两个 叫做全等多边形.相互重合的顶点叫做 ,相互重合的边叫做 ,相互重合的角叫做 .
注 意:(1)一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;
(2)两个全等图形经过上述变换后一定能够互相重合.
2.全等多边形的性质和判定
性 质:全等多边形的对应边 ,对应角 .
判 定: 的两个多边形全等.
3.全等三角形的性质和判定
性 质:全等三角形的对应边、对应角分别 .
判 定:如果两个三角形的 ,那么这两个三角形全等.
类型之一 全等多边形的性质
如图,四边形ABCD与四边形 A'B'C'D' 全等,则∠A= °,∠B= °,B'C'= ,AD= .
类型之二 全等三角形的性质
[2022春·宝安区期中]如图,已知△ABE≌△DCF,且B、F、E、C在同一条直线上.
(1)试说明AB∥CD;
(2)若BC=10,EF=7,求BE的长.
1.下列各组图形中,属于全等图形的是( )
A B
C D
2.如图,四边形ABCD≌四边形A'B'C'D',则∠A的度数是 .
3.如图,已知△ABC与△DBC关于直线BC成轴对称,根据条件填空:
(1)△ABC≌ ;
(2)对应边: 与 , 与 , 与 ;
(3)对应角: 与 , 与 , 与 .
1.下列四个图形中,有两个全等的图形,它们是( )
① ② ③ ④
A.①和② B.②和③
C.②和④ D.③和④
2.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中不一定正确的是( )
A.BE=EC B.BC=EF
C.AC=DF D.△ABC≌△DEF
3.如图,已知△ABC≌△BAD.若∠DAC=20°,∠C=88°,则∠DBA= °.
4.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE= °,EC= .
5.[2022秋·涟水县期中]如图,△ABC≌△DEF,点B、E、C、F在同一条直线上.
(1)若∠BED=140°,∠D=75°,求∠ACB的度数;
(2)若BE=2,EC=3,求BF的长.
6.[2022秋·湖州市长兴县月考]如图,已知△ABC≌△EBD.
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
7.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长;
(2)求∠DBC的度数.
8.(推理能力)如图1,已知△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,C为AD的中点.
(1)求∠BAE的度数和AE的长;
图1
(2)如图2,延长BC,交ED于点F,求∠DFC的度数.
图2
参考答案
【预习导航】
1.完全重合 ≌ 多边形 对应顶点 对应边 对应角 2.相等 相等 边、角分别对应相等
3.相等 边、角分别相等
【归类探究】
【例1】70 85 12 6
【例2】(1)略 (2)BE=8.5
【当堂测评】
1.A 2.95° 3.(1)△DBC (2)AB DB AC DC BC BC (3)∠A ∠D ∠ABC ∠DBC ∠ACB ∠DCB
【分层训练】
1.B 2.A 3.36 4.100 2
5.(1)∠ACB=65° (2)BF=7
6.(1)AD=2 (2)∠ACE=78°
7.(1)AE=6 (2)∠DBC=10°
8.(1)∠BAE=60°,AE=2cm.
(2)∠DFC=150°
。
