第8章 三角形 本章复习课(含答案) 2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 第8章 三角形 本章复习课(含答案) 2024-2025学年数学华东师大版七年级下册 | 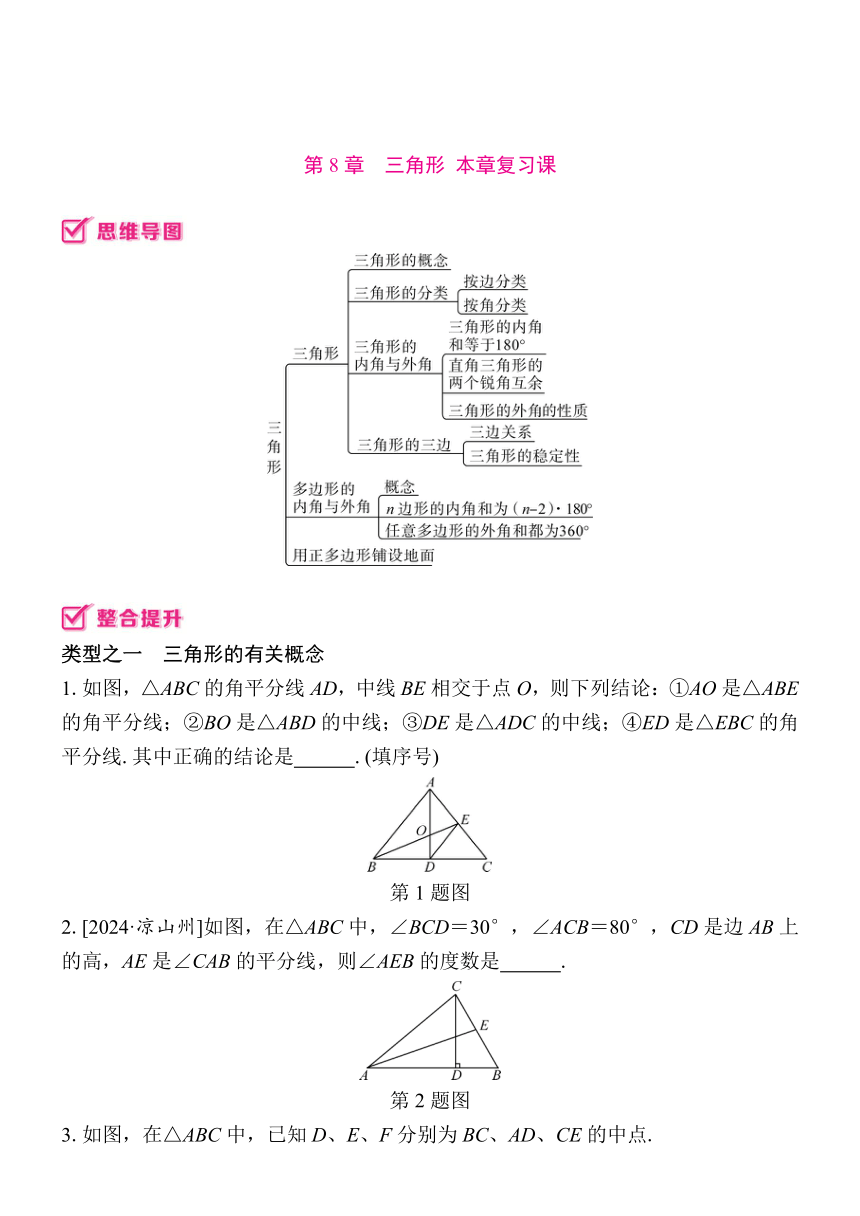 | |
| 格式 | docx | ||
| 文件大小 | 297.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 07:58:30 | ||
图片预览



文档简介
第8章 三角形 本章复习课
类型之一 三角形的有关概念
1.如图,△ABC的角平分线AD,中线BE相交于点O,则下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的结论是 .(填序号)
第1题图
2.[2024·凉山州]如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
第2题图
3.如图,在△ABC中,已知D、E、F分别为BC、AD、CE的中点.
(1)若S△ABC=1,则S△BEF= ;
(2)若S△BFC=1,则S△ABC= .
类型之二 三角形的三边关系
4.[2022秋·贵池区期末]已知a、b、c是△ABC的三边长.
(1)化简:|a-b+c|+|a-b-c|;
(2)若a和b满足方程组且c为偶数,求这个三角形的周长.
类型之三 三角形内角、外角的性质
5.[2024秋·合江县月考]如图,在△ABC中,∠A=60°,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,∠BDC=85°,则∠BDE的度数为 .
6.如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,在△CDA中,DE是边CA上的高,如果∠EDA=∠CDB,求∠B的度数.
7.[2023春·邗江区月考]在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为25°、75°、80°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=20°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=30°,求△ABC中最大内角的度数.
类型之四 多边形的内角和与外角和
8.[2024秋·德阳月考]若某个多边形的内角和是外角和的3倍,则过这个多边形的一个顶点可以引多少条对角线?( )
A.8 B.7 C.6 D.5
9.(1)如图1,∠A+∠B+∠C+∠D+∠E+∠F= ;
图1
(2)如果把图1称为二环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为二环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H,那么二环四边形的内角和为 ;二环五边形的内角和为 ;二环n边形的内角和为 .
图2
1.[2024秋·滑县校级月考]某小组利用延时课进行三角形外角知识的相关研究,制定项目式学习表如下,请你解答任务中的问题.
主题 利用三角形的外角性质进行角度计算和结论探究.
日期 2024年*月*日
成员 组长:* 成员:*
知识储备 三角形的外角等于与它不相邻的两个内角的和.
问题解决
题干 如图,点D在AB上,点E在BC上,AE、CD相交于点P.
任务 (1)若∠A=30°,∠B=40°,∠APC=110°,求∠C的度数; (2)试猜想∠APC与∠A+∠B+∠C之间的关系,并说明理由.
2.[2024春·西岗区校级月考]根据以下情境,探索完成任务.
你研究过三角形的角平分线吗?
问题 背景 在华师版数学教材七年级下册第92页第4题中,我们研究过双内角平分线的夹角的问题,聪聪在研究完该问题后,对这类问题进行了深入的研究.
模型1 如图,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点P,则∠A与∠P之间有一定的数量关系.
模型2 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线交于点P,则∠A与∠P之间有一定的数量关系.
解决问题
任务1 如图,在△ABC中,∠ABC=40°.延长BA至点G,延长AC至点H,已知∠BAC、∠CAG的平分线分别与∠BCH的平分线及其反向延长线交于点E、F,求∠F的度数.
解决问题
任务2 如图,在△ABC中,∠ABC、∠ACB的平分线交于点P,将△ABC沿DE折叠使得点A与点P重合,若∠1+∠2=80°,求∠BPC的度数.
参考答案
【整合提升】
1.①③ 2.100° 3.(1) (2)4
4.(1)2c (2)这个三角形的周长为11或13.
5.25°
6.∠B=60°
7.(1)△ABC是“三倍角三角形”.理由略.
(2)△ABC中最大内角的度数为90°,112.5°或140°.
7.D 8.(1)360°
(2)720° 1 080° 360°(n-2)
【项目化学习】
1.(1)∠C=40°
(2)∠APC=∠A+∠B+∠C.理由略.
2.任务1:∠F=70°
任务2:∠BPC=110°.
。
类型之一 三角形的有关概念
1.如图,△ABC的角平分线AD,中线BE相交于点O,则下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的结论是 .(填序号)
第1题图
2.[2024·凉山州]如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
第2题图
3.如图,在△ABC中,已知D、E、F分别为BC、AD、CE的中点.
(1)若S△ABC=1,则S△BEF= ;
(2)若S△BFC=1,则S△ABC= .
类型之二 三角形的三边关系
4.[2022秋·贵池区期末]已知a、b、c是△ABC的三边长.
(1)化简:|a-b+c|+|a-b-c|;
(2)若a和b满足方程组且c为偶数,求这个三角形的周长.
类型之三 三角形内角、外角的性质
5.[2024秋·合江县月考]如图,在△ABC中,∠A=60°,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,∠BDC=85°,则∠BDE的度数为 .
6.如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,在△CDA中,DE是边CA上的高,如果∠EDA=∠CDB,求∠B的度数.
7.[2023春·邗江区月考]在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为25°、75°、80°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=20°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=30°,求△ABC中最大内角的度数.
类型之四 多边形的内角和与外角和
8.[2024秋·德阳月考]若某个多边形的内角和是外角和的3倍,则过这个多边形的一个顶点可以引多少条对角线?( )
A.8 B.7 C.6 D.5
9.(1)如图1,∠A+∠B+∠C+∠D+∠E+∠F= ;
图1
(2)如果把图1称为二环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为二环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H,那么二环四边形的内角和为 ;二环五边形的内角和为 ;二环n边形的内角和为 .
图2
1.[2024秋·滑县校级月考]某小组利用延时课进行三角形外角知识的相关研究,制定项目式学习表如下,请你解答任务中的问题.
主题 利用三角形的外角性质进行角度计算和结论探究.
日期 2024年*月*日
成员 组长:* 成员:*
知识储备 三角形的外角等于与它不相邻的两个内角的和.
问题解决
题干 如图,点D在AB上,点E在BC上,AE、CD相交于点P.
任务 (1)若∠A=30°,∠B=40°,∠APC=110°,求∠C的度数; (2)试猜想∠APC与∠A+∠B+∠C之间的关系,并说明理由.
2.[2024春·西岗区校级月考]根据以下情境,探索完成任务.
你研究过三角形的角平分线吗?
问题 背景 在华师版数学教材七年级下册第92页第4题中,我们研究过双内角平分线的夹角的问题,聪聪在研究完该问题后,对这类问题进行了深入的研究.
模型1 如图,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点P,则∠A与∠P之间有一定的数量关系.
模型2 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线交于点P,则∠A与∠P之间有一定的数量关系.
解决问题
任务1 如图,在△ABC中,∠ABC=40°.延长BA至点G,延长AC至点H,已知∠BAC、∠CAG的平分线分别与∠BCH的平分线及其反向延长线交于点E、F,求∠F的度数.
解决问题
任务2 如图,在△ABC中,∠ABC、∠ACB的平分线交于点P,将△ABC沿DE折叠使得点A与点P重合,若∠1+∠2=80°,求∠BPC的度数.
参考答案
【整合提升】
1.①③ 2.100° 3.(1) (2)4
4.(1)2c (2)这个三角形的周长为11或13.
5.25°
6.∠B=60°
7.(1)△ABC是“三倍角三角形”.理由略.
(2)△ABC中最大内角的度数为90°,112.5°或140°.
7.D 8.(1)360°
(2)720° 1 080° 360°(n-2)
【项目化学习】
1.(1)∠C=40°
(2)∠APC=∠A+∠B+∠C.理由略.
2.任务1:∠F=70°
任务2:∠BPC=110°.
。
