第9章 轴对称、平移与旋转 滚动训练(五) (含答案) 2024-2025学年数学华东师大版七年级下册
文档属性
| 名称 | 第9章 轴对称、平移与旋转 滚动训练(五) (含答案) 2024-2025学年数学华东师大版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 369.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 00:00:00 | ||
图片预览


文档简介
第9章 轴对称、平移与旋转 滚动训练(五)
一、选择题(每题5分,共30分)
1.下列图形中,是轴对称图形的是( )
A B
C D
2.如图,将△ABC以点C为中心,按逆时针方向旋转75°后得到△A'B'C.若∠ACB=25°,则∠BCA'的度数为( )
第2题图
A.50° B.40° C.25° D.60°
3.如图,在△ABC中,∠B=60°,∠C=50°,D是BC上任意一点,点E和点F分别是点D关于AB和AC的对称点,连结AE和AF,则∠EAF的度数是( )
第3题图
A.140° B.135° C.120° D.100°
4.如图,△ABC平移后得到△DEF,若AE=11,DB=5,则平移的距离是( )
A.6 B.3 C.5 D.11
5.如图,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B'.若点B'、A、C在同一条直线上,则三角板ABC旋转的度数是( )
第5题图
A.60° B.90° C.120° D.150°
6.[2022·天津]如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连结MN,则下列结论一定正确的是( )
第6题图
A.AB=AN
B.AB∥NC
C.∠AMN=∠ACN
D.MN⊥AC
二、填空题(每题4分,共24分)
7.[2024秋·淮安期中]如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为点D,△ABD与△ADB'关于直线AD对称.若∠B'AC=14°,则∠B的度数为 .
第7题图
8.如图,将周长为18cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD的周长为 cm.
第8题图
9.某景区拟在如图所示的长方形水池上架设景观桥.若长方形水池的周长为300m,景观桥宽忽略不计,则小桥总长为 m.
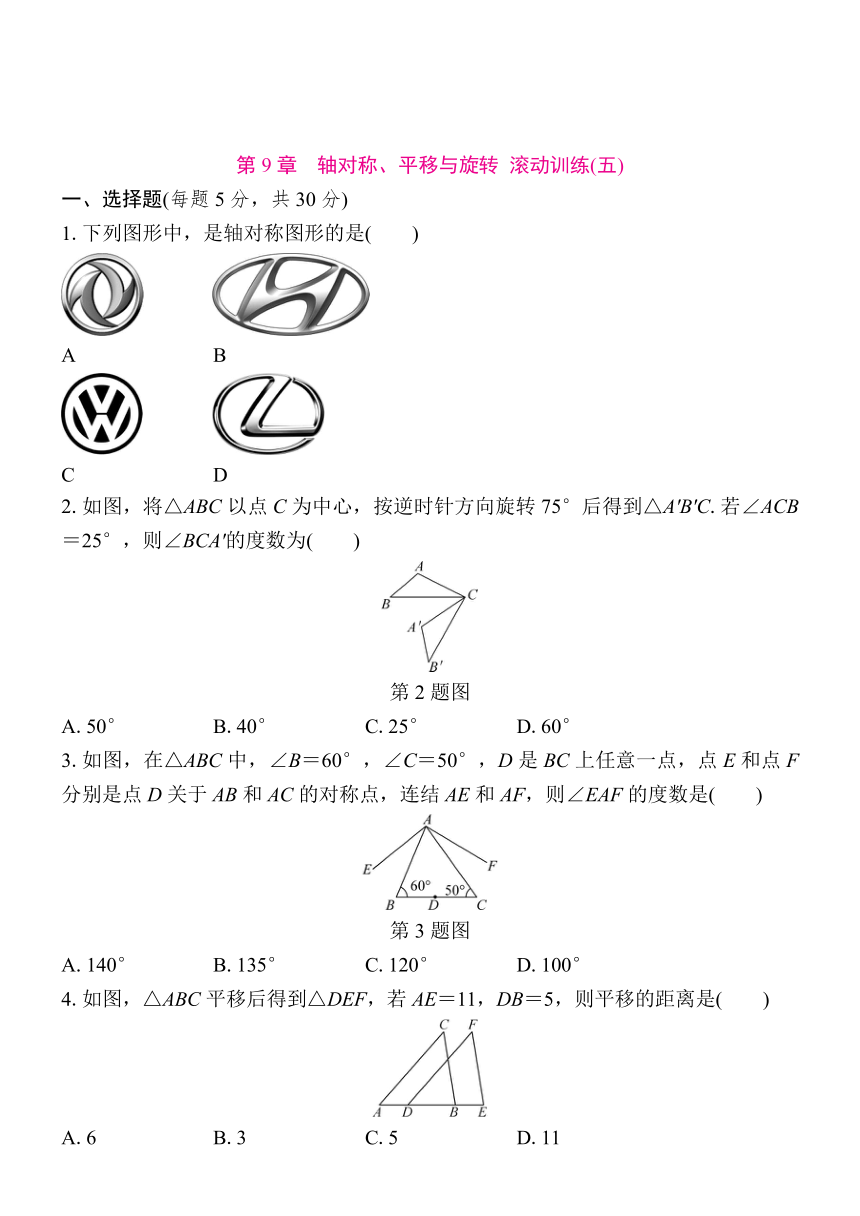
第9题图
10.如图,△COD是△AOB绕点O顺时针旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是 .
第10题图
11.如图是一个旋转对称图形,若将它绕自身中心旋转一定角度之后能与原图重合,则这个角度至少是 .
第11题图
12.[2022秋·江油市期中]如图,在△ABC中,∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一条直线上,则∠E的度数为 .
第12题图
三、解答题(共46分)
13.(12分)[2024·眉山期末]如图所示的10×10正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点均在格点上,点O、M也在格点上,要求只用无刻度的直尺在给定的网格中按要求画图.
(1)画出△ABC先向下平移5个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出△ABC关于直线OM成轴对称的△A2B2C2;
(3)画出△ABC以点O为旋转中心逆时针旋转90°后得到的△A3B3C3;
(4)△ABC的面积是 .
14.(10分)如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种植花草的面积;
(2)若空白的部分种植花草共花费了 4620 元,则每平方米种植花草的费用是多少元?
15.(12分)如图,把一个直角三角板ACB绕着30°角的顶点B顺时针旋转,使得点A与CB延长线上的点E重合.
(1)三角板旋转了 °;
(2)连结CD,试判断△CBD的形状;
(3)求∠BDC的度数.
16.(12分)取两个三角板按图1所示拼接,其中∠ACD=30°,∠ACB=45°.
图1
(1)如图2,三角板ACD固定,将三角板ABC绕点A顺时针旋转一定的角度得到△ABC',当∠CAC'=15°时,请你判断AB与CD的位置关系,并说明理由.
图2
(2)如图3,三角板ACD固定,将三角板ABC绕点A逆时针旋转一定的角度(小于180°)得到△ABC'.猜想当∠CAC'为多少度时,能使CD∥BC'?并说明理由.
图3
参考答案
1.C 2.A 3.A 4.B 5.D 6.C
7.52° 8.20 9.150 10.20° 11.60° 12.65°
13.(1)略 (2)略 (3)略 (4)1.5
14.(1)种植花草的面积为42平方米.
(2)每平方米种植花草的费用是110元.
15.(1)150 (2)△CBD为等腰三角形. (3)∠BDC=15°
16.(1)AB∥CD.理由略.
(2)当∠CAC'=75°时,能使CD∥BC'.理由略.
。
一、选择题(每题5分,共30分)
1.下列图形中,是轴对称图形的是( )
A B
C D
2.如图,将△ABC以点C为中心,按逆时针方向旋转75°后得到△A'B'C.若∠ACB=25°,则∠BCA'的度数为( )
第2题图
A.50° B.40° C.25° D.60°
3.如图,在△ABC中,∠B=60°,∠C=50°,D是BC上任意一点,点E和点F分别是点D关于AB和AC的对称点,连结AE和AF,则∠EAF的度数是( )
第3题图
A.140° B.135° C.120° D.100°
4.如图,△ABC平移后得到△DEF,若AE=11,DB=5,则平移的距离是( )
A.6 B.3 C.5 D.11
5.如图,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B'.若点B'、A、C在同一条直线上,则三角板ABC旋转的度数是( )
第5题图
A.60° B.90° C.120° D.150°
6.[2022·天津]如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连结MN,则下列结论一定正确的是( )
第6题图
A.AB=AN
B.AB∥NC
C.∠AMN=∠ACN
D.MN⊥AC
二、填空题(每题4分,共24分)
7.[2024秋·淮安期中]如图,在Rt△ACB中,∠BAC=90°,AD⊥BC,垂足为点D,△ABD与△ADB'关于直线AD对称.若∠B'AC=14°,则∠B的度数为 .
第7题图
8.如图,将周长为18cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD的周长为 cm.
第8题图
9.某景区拟在如图所示的长方形水池上架设景观桥.若长方形水池的周长为300m,景观桥宽忽略不计,则小桥总长为 m.
第9题图
10.如图,△COD是△AOB绕点O顺时针旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是 .
第10题图
11.如图是一个旋转对称图形,若将它绕自身中心旋转一定角度之后能与原图重合,则这个角度至少是 .
第11题图
12.[2022秋·江油市期中]如图,在△ABC中,∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一条直线上,则∠E的度数为 .
第12题图
三、解答题(共46分)
13.(12分)[2024·眉山期末]如图所示的10×10正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点均在格点上,点O、M也在格点上,要求只用无刻度的直尺在给定的网格中按要求画图.
(1)画出△ABC先向下平移5个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出△ABC关于直线OM成轴对称的△A2B2C2;
(3)画出△ABC以点O为旋转中心逆时针旋转90°后得到的△A3B3C3;
(4)△ABC的面积是 .
14.(10分)如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种植花草的面积;
(2)若空白的部分种植花草共花费了 4620 元,则每平方米种植花草的费用是多少元?
15.(12分)如图,把一个直角三角板ACB绕着30°角的顶点B顺时针旋转,使得点A与CB延长线上的点E重合.
(1)三角板旋转了 °;
(2)连结CD,试判断△CBD的形状;
(3)求∠BDC的度数.
16.(12分)取两个三角板按图1所示拼接,其中∠ACD=30°,∠ACB=45°.
图1
(1)如图2,三角板ACD固定,将三角板ABC绕点A顺时针旋转一定的角度得到△ABC',当∠CAC'=15°时,请你判断AB与CD的位置关系,并说明理由.
图2
(2)如图3,三角板ACD固定,将三角板ABC绕点A逆时针旋转一定的角度(小于180°)得到△ABC'.猜想当∠CAC'为多少度时,能使CD∥BC'?并说明理由.
图3
参考答案
1.C 2.A 3.A 4.B 5.D 6.C
7.52° 8.20 9.150 10.20° 11.60° 12.65°
13.(1)略 (2)略 (3)略 (4)1.5
14.(1)种植花草的面积为42平方米.
(2)每平方米种植花草的费用是110元.
15.(1)150 (2)△CBD为等腰三角形. (3)∠BDC=15°
16.(1)AB∥CD.理由略.
(2)当∠CAC'=75°时,能使CD∥BC'.理由略.
。
