2024-2025学年河南省南阳六校高一(上)期末数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河南省南阳六校高一(上)期末数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 36.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 00:00:00 | ||
图片预览


文档简介
2024-2025学年河南省南阳六校高一(上)期末数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知函数,则( )
A. B. C. D.
3.“,”成立的一个必要不充分条件是( )
A. B. C. D.
4.将个数据按照从小到大的顺序排列如下:,,,,,,,,,,若该组数据的分位数是,则( )
A. B. C. D.
5.设,,,则( )
A. B. C. D.
6.已知是定义域为的奇函数,,且当时,单调递增,则满足不等式的的取值范围是( )
A. B.
C. D.
7.设函数,若恰有两个零点,则实数的取值范围是( )
A. B. ,
C. D.
8.已知函数,,若在区间上的值域为,则在上的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知关于的不等式的解集为,则( )
A.
B. 不等式的解集为
C. 函数在定义域内单调递增
D. 的最小值为
10.已知事件,发生的概率分别为,,则下列说法正确的是( )
A. 若发生时一定发生,则
B. 若与互斥,则和都不发生的概率为
C. 若,则与相互独立
D. 若与相互独立,则
11.函数,被称为“狄利克雷函数”,函数,被称为“符号函数”,这两个函数在数学和计算机等领域中有着广泛的应用下列有关这两个函数的说法正确的是( )
A.
B. 是偶函数
C. 存在两个正无理数,,满足
D. 存在四个点,,,,使得四边形为正方形
三、填空题:本题共3小题,每小题5分,共15分。
12.设且,则函数的图象恒过点______.
13.甲、乙两个研究小组独立攻坚一项关键技术,假设甲组成功的概率为,乙组成功的概率为,则这项技术研究成功的概率为______.
14.已知实数,满足,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
近些年来,我国外卖业发展迅猛,外卖骑手穿梭在城市的大街小巷,成为一道亮丽的风景线某课外实践小组随机调查了该市的名外卖骑手,统计他们的日单量平均每天送的外卖单数,数据如表:
Ⅰ估计该市的外卖骑手日单量大于的概率;
Ⅱ求这名外卖骑手日单量的平均数和方差;
Ⅲ若表中第一行数据对应的外卖骑手来自甲公司,第二行数据对应的外卖骑手来自乙公司,试判断:哪家公司的外卖骑手日单量的差异更大?直接给出结论即可,不需要写计算过程
16.本小题分
已知是奇函数,且.
Ⅰ求的解析式;
Ⅱ若,求实数的取值范围.
17.本小题分
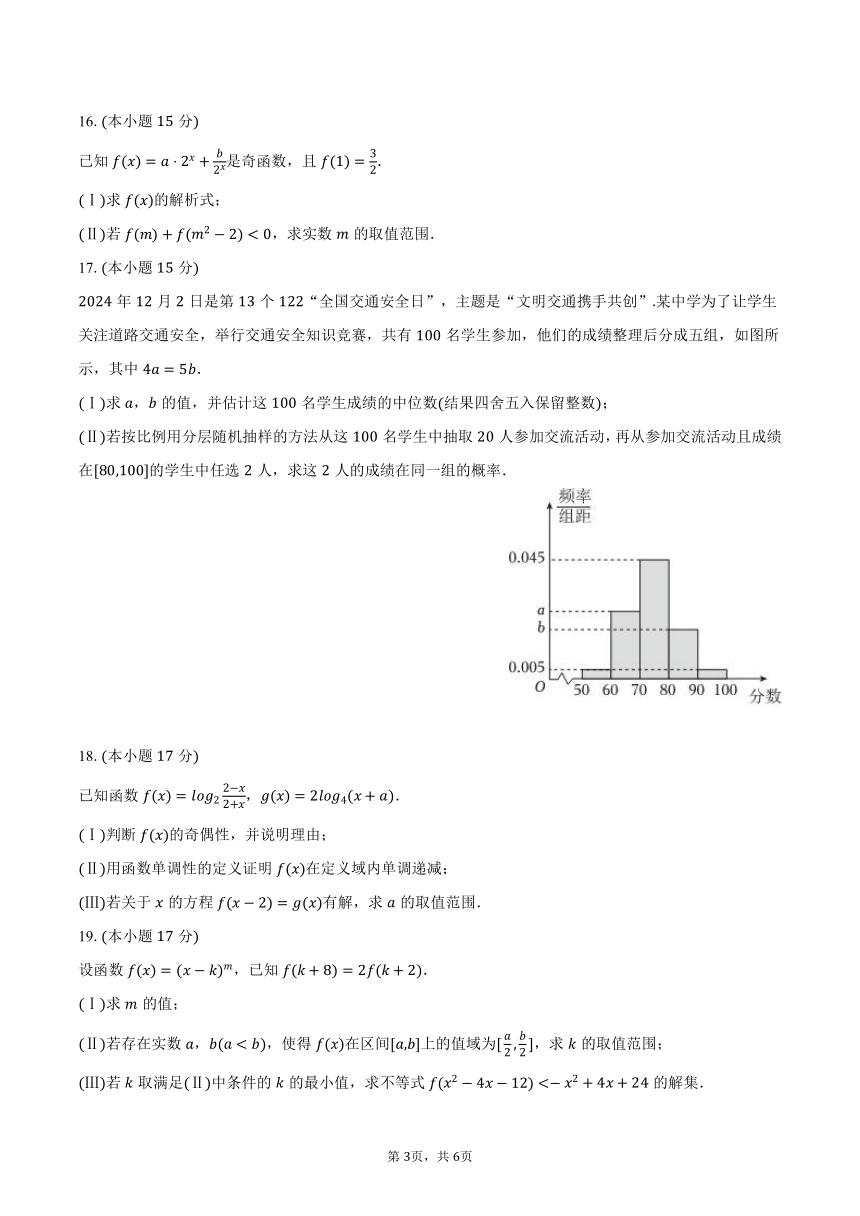
年月日是第个“全国交通安全日”,主题是“文明交通携手共创”某中学为了让学生关注道路交通安全,举行交通安全知识竞赛,共有名学生参加,他们的成绩整理后分成五组,如图所示,其中.
Ⅰ求,的值,并估计这名学生成绩的中位数结果四舍五入保留整数;
Ⅱ若按比例用分层随机抽样的方法从这名学生中抽取人参加交流活动,再从参加交流活动且成绩在的学生中任选人,求这人的成绩在同一组的概率.
18.本小题分
已知函数,.
Ⅰ判断的奇偶性,并说明理由;
Ⅱ用函数单调性的定义证明在定义域内单调递减;
Ⅲ若关于的方程有解,求的取值范围.
19.本小题分
设函数,已知.
Ⅰ求的值;
Ⅱ若存在实数,,使得在区间上的值域为,求的取值范围;
Ⅲ若取满足Ⅱ中条件的的最小值,求不等式的解集.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:Ⅰ名外卖骑手中有人的日单量大于,频率为,
因此估计该市的外卖骑手日单量大于的概率为;
Ⅱ平均数为,
方差为;
Ⅲ乙公司的外卖骑手日单量的差异更大.
16.解:,
是奇函数,且的定义域为,,
由,得,.
故.
经检验,此时是奇函数,符合题意.
Ⅱ,
又为奇函数,
和都在上单调递增,在上单调递增.
,即,解得,
即的取值范围是.
17.解:Ⅰ根据题意可得,
解得,;
前几组的频率依次为,,,
估计这名学生成绩的中位数为;
Ⅱ与两组的频率之比为::,
在中抽取人,在中抽取人,
再从这人中任选人,这人的成绩在同一组的概率为.
18.解析Ⅰ由题意得,得,即的定义域为.
因为,
所以是奇函数.
Ⅱ由Ⅰ知的定义域为,任取,
因为,所以,
所以,所以
即,
所以在定义域内单调递减.
Ⅲ,且由,得,
,
因为关于的方程有解,所以方程在区间上有解,
即在区间上有解.
因为和均在区间上单调递减,所以在区间上单调递减,
所以当时,的取值范围是.
令,得,
即的取值范围是.
19.解:Ⅰ,,即,
,;
Ⅱ由Ⅰ知,则在上单调递增,
在区间上的值域为,,,
方程有两个不相等的实根,则且,
方程在,上有两个不相等的实根.
,解得,
的取值范围是;
Ⅲ由题意知,
由,得
整理得,
设函数,则在上单调递增,注意到,
原不等式等价于,
由,解得或,由,解得,
原不等式的解集为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知函数,则( )
A. B. C. D.
3.“,”成立的一个必要不充分条件是( )
A. B. C. D.
4.将个数据按照从小到大的顺序排列如下:,,,,,,,,,,若该组数据的分位数是,则( )
A. B. C. D.
5.设,,,则( )
A. B. C. D.
6.已知是定义域为的奇函数,,且当时,单调递增,则满足不等式的的取值范围是( )
A. B.
C. D.
7.设函数,若恰有两个零点,则实数的取值范围是( )
A. B. ,
C. D.
8.已知函数,,若在区间上的值域为,则在上的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知关于的不等式的解集为,则( )
A.
B. 不等式的解集为
C. 函数在定义域内单调递增
D. 的最小值为
10.已知事件,发生的概率分别为,,则下列说法正确的是( )
A. 若发生时一定发生,则
B. 若与互斥,则和都不发生的概率为
C. 若,则与相互独立
D. 若与相互独立,则
11.函数,被称为“狄利克雷函数”,函数,被称为“符号函数”,这两个函数在数学和计算机等领域中有着广泛的应用下列有关这两个函数的说法正确的是( )
A.
B. 是偶函数
C. 存在两个正无理数,,满足
D. 存在四个点,,,,使得四边形为正方形
三、填空题:本题共3小题,每小题5分,共15分。
12.设且,则函数的图象恒过点______.
13.甲、乙两个研究小组独立攻坚一项关键技术,假设甲组成功的概率为,乙组成功的概率为,则这项技术研究成功的概率为______.
14.已知实数,满足,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
近些年来,我国外卖业发展迅猛,外卖骑手穿梭在城市的大街小巷,成为一道亮丽的风景线某课外实践小组随机调查了该市的名外卖骑手,统计他们的日单量平均每天送的外卖单数,数据如表:
Ⅰ估计该市的外卖骑手日单量大于的概率;
Ⅱ求这名外卖骑手日单量的平均数和方差;
Ⅲ若表中第一行数据对应的外卖骑手来自甲公司,第二行数据对应的外卖骑手来自乙公司,试判断:哪家公司的外卖骑手日单量的差异更大?直接给出结论即可,不需要写计算过程
16.本小题分
已知是奇函数,且.
Ⅰ求的解析式;
Ⅱ若,求实数的取值范围.
17.本小题分
年月日是第个“全国交通安全日”,主题是“文明交通携手共创”某中学为了让学生关注道路交通安全,举行交通安全知识竞赛,共有名学生参加,他们的成绩整理后分成五组,如图所示,其中.
Ⅰ求,的值,并估计这名学生成绩的中位数结果四舍五入保留整数;
Ⅱ若按比例用分层随机抽样的方法从这名学生中抽取人参加交流活动,再从参加交流活动且成绩在的学生中任选人,求这人的成绩在同一组的概率.
18.本小题分
已知函数,.
Ⅰ判断的奇偶性,并说明理由;
Ⅱ用函数单调性的定义证明在定义域内单调递减;
Ⅲ若关于的方程有解,求的取值范围.
19.本小题分
设函数,已知.
Ⅰ求的值;
Ⅱ若存在实数,,使得在区间上的值域为,求的取值范围;
Ⅲ若取满足Ⅱ中条件的的最小值,求不等式的解集.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:Ⅰ名外卖骑手中有人的日单量大于,频率为,
因此估计该市的外卖骑手日单量大于的概率为;
Ⅱ平均数为,
方差为;
Ⅲ乙公司的外卖骑手日单量的差异更大.
16.解:,
是奇函数,且的定义域为,,
由,得,.
故.
经检验,此时是奇函数,符合题意.
Ⅱ,
又为奇函数,
和都在上单调递增,在上单调递增.
,即,解得,
即的取值范围是.
17.解:Ⅰ根据题意可得,
解得,;
前几组的频率依次为,,,
估计这名学生成绩的中位数为;
Ⅱ与两组的频率之比为::,
在中抽取人,在中抽取人,
再从这人中任选人,这人的成绩在同一组的概率为.
18.解析Ⅰ由题意得,得,即的定义域为.
因为,
所以是奇函数.
Ⅱ由Ⅰ知的定义域为,任取,
因为,所以,
所以,所以
即,
所以在定义域内单调递减.
Ⅲ,且由,得,
,
因为关于的方程有解,所以方程在区间上有解,
即在区间上有解.
因为和均在区间上单调递减,所以在区间上单调递减,
所以当时,的取值范围是.
令,得,
即的取值范围是.
19.解:Ⅰ,,即,
,;
Ⅱ由Ⅰ知,则在上单调递增,
在区间上的值域为,,,
方程有两个不相等的实根,则且,
方程在,上有两个不相等的实根.
,解得,
的取值范围是;
Ⅲ由题意知,
由,得
整理得,
设函数,则在上单调递增,注意到,
原不等式等价于,
由,解得或,由,解得,
原不等式的解集为.
第1页,共1页
同课章节目录
