图形的旋转
图片预览




文档简介
课件23张PPT。 图 形 的 旋 转(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?归纳:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。议一议:如图△ABC绕着旋转中心按逆时针旋转θ后,得到△A′B′C′BACB′A′C′O点B的对应点是点 ;
线段AB的对应线段是线段 ;
线段BC的对应线段是线段 ;
∠A的对应角是 ;
∠B的对应角是 ;
旋转中心是点 ;
旋转的角度是 .(1)连接OA,OB,OC,OA′,OB′,OC′,
那么OA与OA′长度有什么关系?
OB与OB′,OC和OC′也有这样的关系吗?
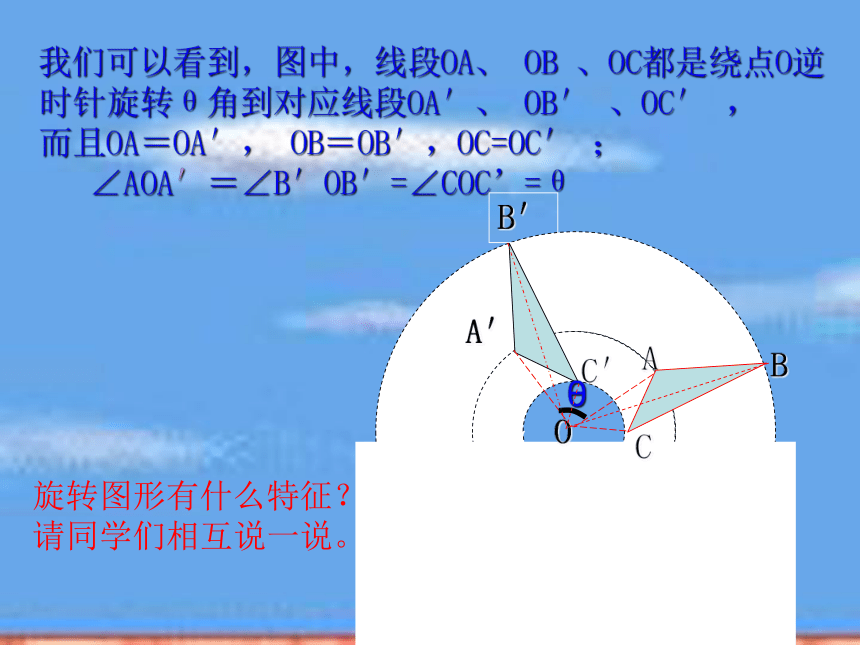
(2)∠AOA′,∠BOB′,∠COC′有何关系我们可以看到,图中,线段OA、 OB 、OC都是绕点O逆时针旋转θ角到对应线段OA′、 OB′ 、OC′ , 而且OA=OA′, OB=OB′,OC=OC′ ; ∠AOA′=∠B′OB′=∠COC’=θ旋转图形有什么特征?
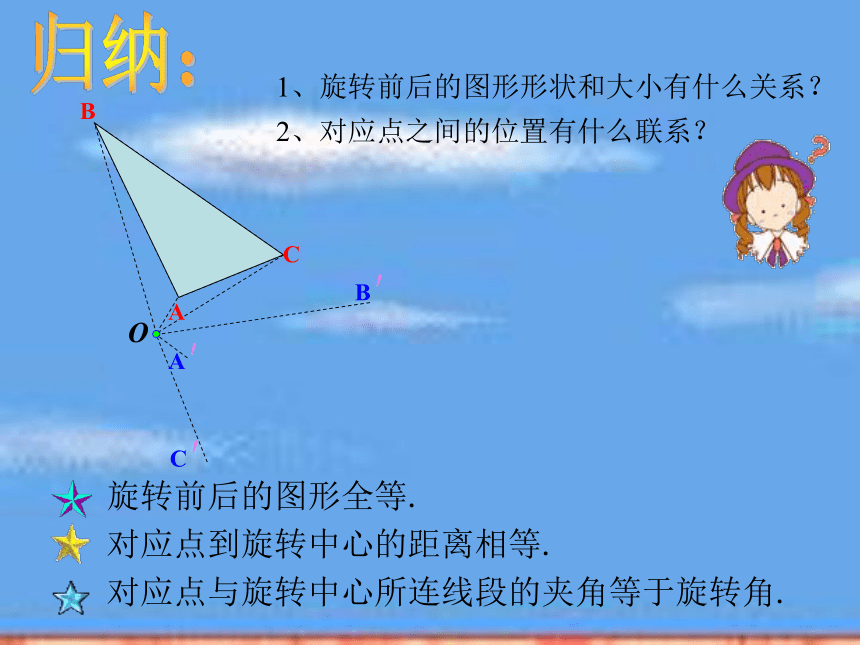
请同学们相互说一说。θ归纳:1、旋转前后的图形形状和大小有什么关系?
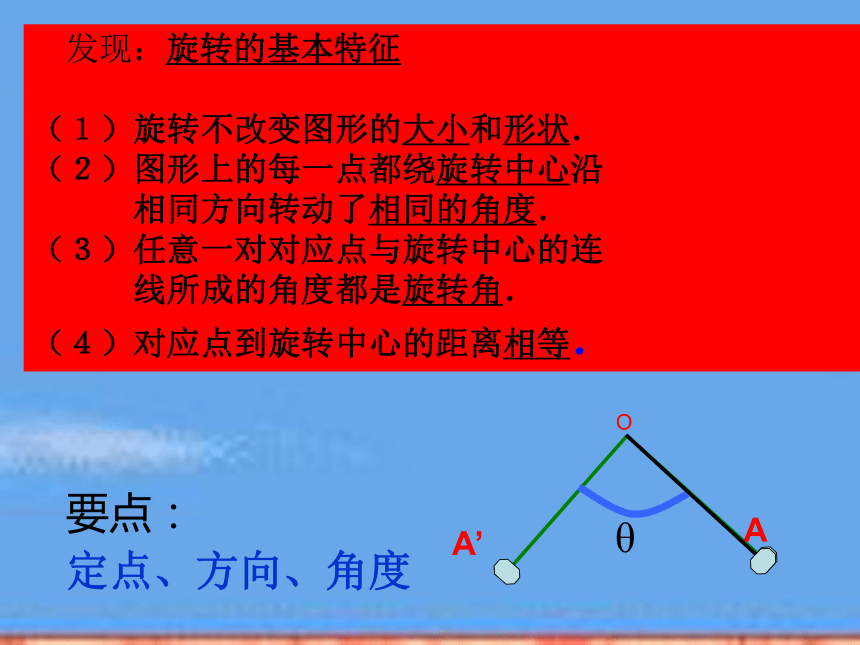
2、对应点之间的位置有什么联系?O 发现:旋转的基本特征
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.要点:
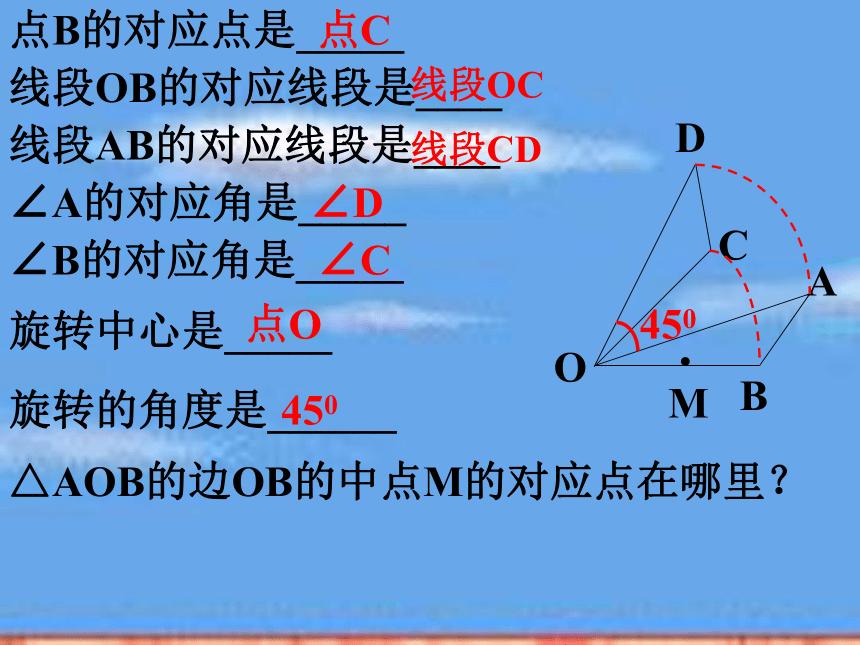
定点、方向、角度A’AOO点B的对应点是_____线段OB的对应线段是____线段AB的对应线段是____∠A的对应角是_____∠B的对应角是_____旋转中心是_____旋转的角度是______点C线段OC线段CD∠D∠C点O450△AOB的边OB的中点M的对应点在哪里?例1:在下图中,画出三角形ABC绕点O按逆时针方向旋转45°后的图形解:
1,连结OA,OB,OC
2以OA为始边,逆时针方向作45°角,
在角的终边上截取线段OA,,使OA=OA,
得道点A
3,同样分别可得B,C的对应点BC
4,联接AB BC AC
所得到的三角形ABC就是三角形ABC绕点O
按逆时针方向旋转45°后的图形例2:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?解:
(1)它的旋转中心是
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为钟表的轴心ABDCEM·例3、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE位置。
1、旋转中心是哪一点
2、旋转了多少度?
3、如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?点A60°点M转到了线段AC的中点上(2)旋转角是几度?例4 如图△ABC为等边三角形,△ABP旋转后能与△CBP1重合,那么
(1)旋转中心是哪一点
′B60°等边三角形1下列 运动属于旋转的是( )
A滚动过程中的篮球
C气球升空的运动 D一个图形沿某直线对折过程
2下列说法不正确的是( )
A旋转中心在旋转过程中是不动的
B旋转形成的图形由旋转中心和旋转角共同决定的
C旋转不改变图形的形状和大小
D旋转改变图形的形状但不改变大小针对性训练:B钟表的钟摆运动3、将图形 按顺时针方向旋转90度后的图形是ABCD针对性训练:4、如图,直角△AOB 顺时针旋转后与△COD重合,若∠AOD=127°,则旋转角度是 °
5、如图,已知∠EAD=30°,△ADE 绕着点A旋转50°后能与△ABC重合,则∠BAE= 度. 针对性训练:2045针对性训练:6下列图形是不是旋转对称图形?如果是,那么需要旋转多少度可以与原图形重合. 在图中,正方形ABCD与正方形 EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.?ACBDEFGH1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
请思考平移和旋转的异同点?归纳小结一:旋转的概念
定点,方向,旋转角
二:旋转的特征
变量和不变量,对应点
归纳小结一:旋转的概念
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角
定点,方向,旋转角
二:旋转的特征
旋转不改变图形的大小和形状.
1、收集生活中旋转图形的实例.作业布置2、一课一练。P108,11.2 旋转
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?归纳:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。议一议:如图△ABC绕着旋转中心按逆时针旋转θ后,得到△A′B′C′BACB′A′C′O点B的对应点是点 ;
线段AB的对应线段是线段 ;
线段BC的对应线段是线段 ;
∠A的对应角是 ;
∠B的对应角是 ;
旋转中心是点 ;
旋转的角度是 .(1)连接OA,OB,OC,OA′,OB′,OC′,
那么OA与OA′长度有什么关系?
OB与OB′,OC和OC′也有这样的关系吗?
(2)∠AOA′,∠BOB′,∠COC′有何关系我们可以看到,图中,线段OA、 OB 、OC都是绕点O逆时针旋转θ角到对应线段OA′、 OB′ 、OC′ , 而且OA=OA′, OB=OB′,OC=OC′ ; ∠AOA′=∠B′OB′=∠COC’=θ旋转图形有什么特征?
请同学们相互说一说。θ归纳:1、旋转前后的图形形状和大小有什么关系?
2、对应点之间的位置有什么联系?O 发现:旋转的基本特征
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连
线所成的角度都是旋转角.
(4)对应点到旋转中心的距离相等.要点:
定点、方向、角度A’AOO点B的对应点是_____线段OB的对应线段是____线段AB的对应线段是____∠A的对应角是_____∠B的对应角是_____旋转中心是_____旋转的角度是______点C线段OC线段CD∠D∠C点O450△AOB的边OB的中点M的对应点在哪里?例1:在下图中,画出三角形ABC绕点O按逆时针方向旋转45°后的图形解:
1,连结OA,OB,OC
2以OA为始边,逆时针方向作45°角,
在角的终边上截取线段OA,,使OA=OA,
得道点A
3,同样分别可得B,C的对应点BC
4,联接AB BC AC
所得到的三角形ABC就是三角形ABC绕点O
按逆时针方向旋转45°后的图形例2:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?解:
(1)它的旋转中心是
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为钟表的轴心ABDCEM·例3、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE位置。
1、旋转中心是哪一点
2、旋转了多少度?
3、如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?点A60°点M转到了线段AC的中点上(2)旋转角是几度?例4 如图△ABC为等边三角形,△ABP旋转后能与△CBP1重合,那么
(1)旋转中心是哪一点
′B60°等边三角形1下列 运动属于旋转的是( )
A滚动过程中的篮球
C气球升空的运动 D一个图形沿某直线对折过程
2下列说法不正确的是( )
A旋转中心在旋转过程中是不动的
B旋转形成的图形由旋转中心和旋转角共同决定的
C旋转不改变图形的形状和大小
D旋转改变图形的形状但不改变大小针对性训练:B钟表的钟摆运动3、将图形 按顺时针方向旋转90度后的图形是ABCD针对性训练:4、如图,直角△AOB 顺时针旋转后与△COD重合,若∠AOD=127°,则旋转角度是 °
5、如图,已知∠EAD=30°,△ADE 绕着点A旋转50°后能与△ABC重合,则∠BAE= 度. 针对性训练:2045针对性训练:6下列图形是不是旋转对称图形?如果是,那么需要旋转多少度可以与原图形重合. 在图中,正方形ABCD与正方形 EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.?ACBDEFGH1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
请思考平移和旋转的异同点?归纳小结一:旋转的概念
定点,方向,旋转角
二:旋转的特征
变量和不变量,对应点
归纳小结一:旋转的概念
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角
定点,方向,旋转角
二:旋转的特征
旋转不改变图形的大小和形状.
1、收集生活中旋转图形的实例.作业布置2、一课一练。P108,11.2 旋转
