2.4 有理数的乘方(2) 课件(共17张PPT)北师大版数学七年级上册
文档属性
| 名称 | 2.4 有理数的乘方(2) 课件(共17张PPT)北师大版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 420.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 12:20:58 | ||
图片预览






文档简介
(共17张PPT)
第二章 有理数及其运算
2.4 有理数的乘方(2)
你相信吗?
如果用 1 表示原地踏步,1.01表示一天进步1%,0.99是一天退步1%。一天下来,进步与退步者的差距只有0.02。可是365天之后,他们的差距就扩大到1260倍,你相信吗?
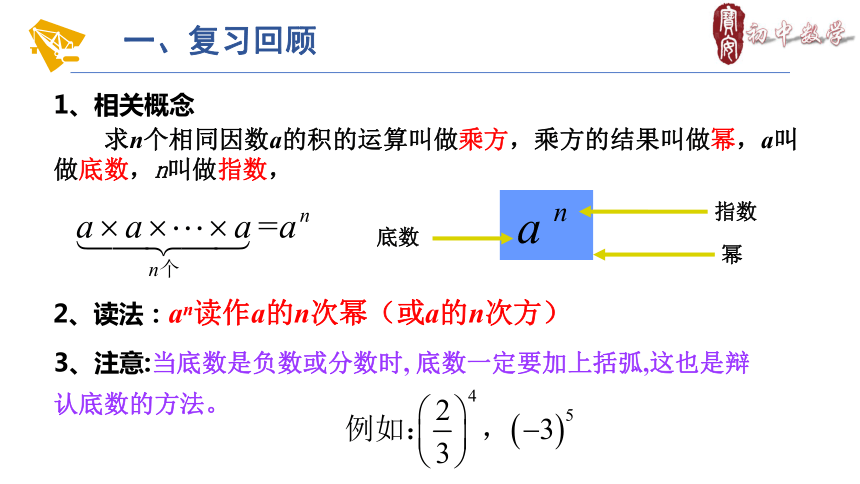
1、相关概念
求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,
底数
指数
幂
一、复习回顾
2、读法:an读作a的n次幂(或a的n次方)
3、注意:当底数是负数或分数时, 底数一定要加上括弧,这也是辩认底数的方法。
(-2)4 -24
4、说出下列乘方的底数、读法、意义及计算结果
底数:
读法:
意义:
结果:
(-2)4 的底数是-2,-24 底数是2
(-2)4 读作-2的4次方,-24 读作2的4次方的相反数
(-2)4 表示4个-2相乘,-24 表示4个2相乘的相反数
(-2)4 =16,-24 = -16.
二、新知初探,归纳法则
计算:
1
例3
有理数乘法符号法则:两数相乘,同号得正,异号得负。几个不为0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负,当负因数有偶数个时,积为正.
1.底数为10的幂的特点:
10的n次幂等于1的后面有n个0.
2.有理数乘方运算的符号法则 :
正数的任何次幂都是正数,
负数的偶数次幂是正数,
负数的奇数次幂是负数.
1
-1
二、新知初探,归纳法则
1、将它对折1次后,厚度为_____________毫米.
有一张厚度为0.1毫米的纸,将它对折.
2、将它对折2次后,厚度为_____________毫米.
3、对折20次后,厚度为多少毫米?假如每层楼平均高度为3m ,这张纸对折20次后有多少层楼高?
4、通过这个活动,你从中得到了什么启示
三、新知再探,折纸问题
22
23
24
5
20
2×2=
2×2×2=
2×2×2×2=
2×2×2×2×2=
2×2× … ×2=
20次
21
2=
折1次
折2次
折3次
折4次
折5次
折20次
折纸与楼高
折纸的层次
折纸的厚度
1、将它对折1次后,厚度为_____________毫米.
有一张厚度为0.1毫米的纸,将它对折.
2、将它对折2次后,厚度为_____________毫米.
折纸与楼高
0.2
0.4
3、有一张厚度为0.1毫米的纸,将它对折20次后,厚度为多少毫米?假如每层楼平均高度为3m ,这张纸对折20次后有多少层楼高?
解:对折20次后的厚度为
0.1×220 =0.1×1048576=104857.6 (mm)
=104.8576 (m)
104.8576 ÷ 3 35
所以对折20次后的厚度大约是35层楼的高度.
折纸与楼高
当指数不断增加时,底数大于1 的幂的增长速度相当快
折纸与楼高
4、通过这个活动,你从中得到了什么启示
拉面师傅把一根粗面条拉长、两头捏合,再拉长、捏合,重复这样,就拉成许多根细面条了.据报道,在一次比赛中,某拉面师傅用1kg面粉拉出约209万根面条,你知道怎样得出这个结果的吗?
第一次
拉扣后
第二次
拉扣后
第三次
拉扣后
…
四、应用新知,解决问题
所以,拉面师傅拉扣21次,能拉出约209万根面条。
1根
2根
4根
8根
一起感受乘方的力量
当指数不断增加时,底数大于1 的幂的增长速度相当快
当指数不断增加时,底数小于1 (正数)的幂的减小速度相当快
如果用 1 表示原地踏步,1.01表示一天进步1%,0.99是一天退步1%。一天下来,进步与退步者的差距只有0.02。可是365天之后,他们的差距就扩大到1260倍,你相信吗?
五、巩固训练,提升能力
正
负
负
正
负数的偶数次幂是正数,负数的奇数次幂是负数.
五、巩固训练,提升能力
思考:如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
(1)阴影部分的面积是_____________;
1.底数为10的幂的特点:
10的n次幂等于1的后面有n个0.
2.有理数乘方运算的符号法则 :
正数的任何次幂都是正数,
负数的偶数次幂是正数,
负数的奇数次幂是负数.
六、课堂小结,升华认知
1
-1
3.幂的变化速度:
当指数不断增加时,底数大于1 的幂的增长速度相当快
当指数不断增加时,底数小于1 (正数)的幂的减小速度相当快
“乘方”精神:人生中,差别不大的0.01不可小觑,微小的勤奋只要坚持下去也会成就非凡,微小的惰性日积月累亦会带来巨大的失败;人与人之间的初始差别往往就在于0.01,人生之路漫长,每天如同登山般,只要是往上走,即便每天一小步,也会创造人生的新高度。
教师寄语
第二章 有理数及其运算
2.4 有理数的乘方(2)
你相信吗?
如果用 1 表示原地踏步,1.01表示一天进步1%,0.99是一天退步1%。一天下来,进步与退步者的差距只有0.02。可是365天之后,他们的差距就扩大到1260倍,你相信吗?
1、相关概念
求n个相同因数a的积的运算叫做乘方,乘方的结果叫做幂,a叫做底数,n叫做指数,
底数
指数
幂
一、复习回顾
2、读法:an读作a的n次幂(或a的n次方)
3、注意:当底数是负数或分数时, 底数一定要加上括弧,这也是辩认底数的方法。
(-2)4 -24
4、说出下列乘方的底数、读法、意义及计算结果
底数:
读法:
意义:
结果:
(-2)4 的底数是-2,-24 底数是2
(-2)4 读作-2的4次方,-24 读作2的4次方的相反数
(-2)4 表示4个-2相乘,-24 表示4个2相乘的相反数
(-2)4 =16,-24 = -16.
二、新知初探,归纳法则
计算:
1
例3
有理数乘法符号法则:两数相乘,同号得正,异号得负。几个不为0的数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积为负,当负因数有偶数个时,积为正.
1.底数为10的幂的特点:
10的n次幂等于1的后面有n个0.
2.有理数乘方运算的符号法则 :
正数的任何次幂都是正数,
负数的偶数次幂是正数,
负数的奇数次幂是负数.
1
-1
二、新知初探,归纳法则
1、将它对折1次后,厚度为_____________毫米.
有一张厚度为0.1毫米的纸,将它对折.
2、将它对折2次后,厚度为_____________毫米.
3、对折20次后,厚度为多少毫米?假如每层楼平均高度为3m ,这张纸对折20次后有多少层楼高?
4、通过这个活动,你从中得到了什么启示
三、新知再探,折纸问题
22
23
24
5
20
2×2=
2×2×2=
2×2×2×2=
2×2×2×2×2=
2×2× … ×2=
20次
21
2=
折1次
折2次
折3次
折4次
折5次
折20次
折纸与楼高
折纸的层次
折纸的厚度
1、将它对折1次后,厚度为_____________毫米.
有一张厚度为0.1毫米的纸,将它对折.
2、将它对折2次后,厚度为_____________毫米.
折纸与楼高
0.2
0.4
3、有一张厚度为0.1毫米的纸,将它对折20次后,厚度为多少毫米?假如每层楼平均高度为3m ,这张纸对折20次后有多少层楼高?
解:对折20次后的厚度为
0.1×220 =0.1×1048576=104857.6 (mm)
=104.8576 (m)
104.8576 ÷ 3 35
所以对折20次后的厚度大约是35层楼的高度.
折纸与楼高
当指数不断增加时,底数大于1 的幂的增长速度相当快
折纸与楼高
4、通过这个活动,你从中得到了什么启示
拉面师傅把一根粗面条拉长、两头捏合,再拉长、捏合,重复这样,就拉成许多根细面条了.据报道,在一次比赛中,某拉面师傅用1kg面粉拉出约209万根面条,你知道怎样得出这个结果的吗?
第一次
拉扣后
第二次
拉扣后
第三次
拉扣后
…
四、应用新知,解决问题
所以,拉面师傅拉扣21次,能拉出约209万根面条。
1根
2根
4根
8根
一起感受乘方的力量
当指数不断增加时,底数大于1 的幂的增长速度相当快
当指数不断增加时,底数小于1 (正数)的幂的减小速度相当快
如果用 1 表示原地踏步,1.01表示一天进步1%,0.99是一天退步1%。一天下来,进步与退步者的差距只有0.02。可是365天之后,他们的差距就扩大到1260倍,你相信吗?
五、巩固训练,提升能力
正
负
负
正
负数的偶数次幂是正数,负数的奇数次幂是负数.
五、巩固训练,提升能力
思考:如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
(1)阴影部分的面积是_____________;
1.底数为10的幂的特点:
10的n次幂等于1的后面有n个0.
2.有理数乘方运算的符号法则 :
正数的任何次幂都是正数,
负数的偶数次幂是正数,
负数的奇数次幂是负数.
六、课堂小结,升华认知
1
-1
3.幂的变化速度:
当指数不断增加时,底数大于1 的幂的增长速度相当快
当指数不断增加时,底数小于1 (正数)的幂的减小速度相当快
“乘方”精神:人生中,差别不大的0.01不可小觑,微小的勤奋只要坚持下去也会成就非凡,微小的惰性日积月累亦会带来巨大的失败;人与人之间的初始差别往往就在于0.01,人生之路漫长,每天如同登山般,只要是往上走,即便每天一小步,也会创造人生的新高度。
教师寄语
同课章节目录
