19.2勾股定理
图片预览




文档简介
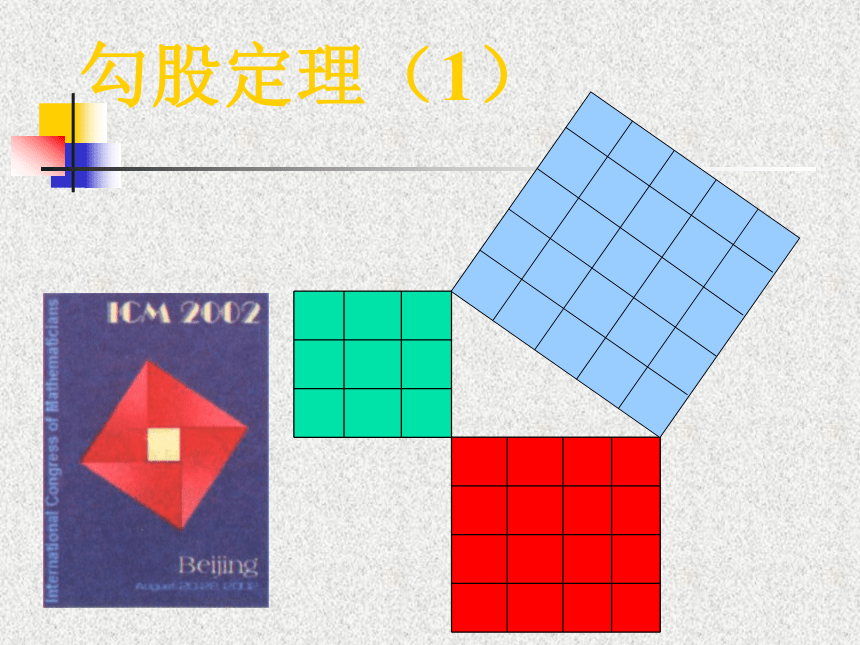
课件36张PPT。 勾股定理(1)回忆:
我们学过直角三角形的哪些性质?我们来进一步研究直角三角形的边所具有的性质问题一
在直角三角形中,直角边与斜边之间有怎样的大小关系?为什么?
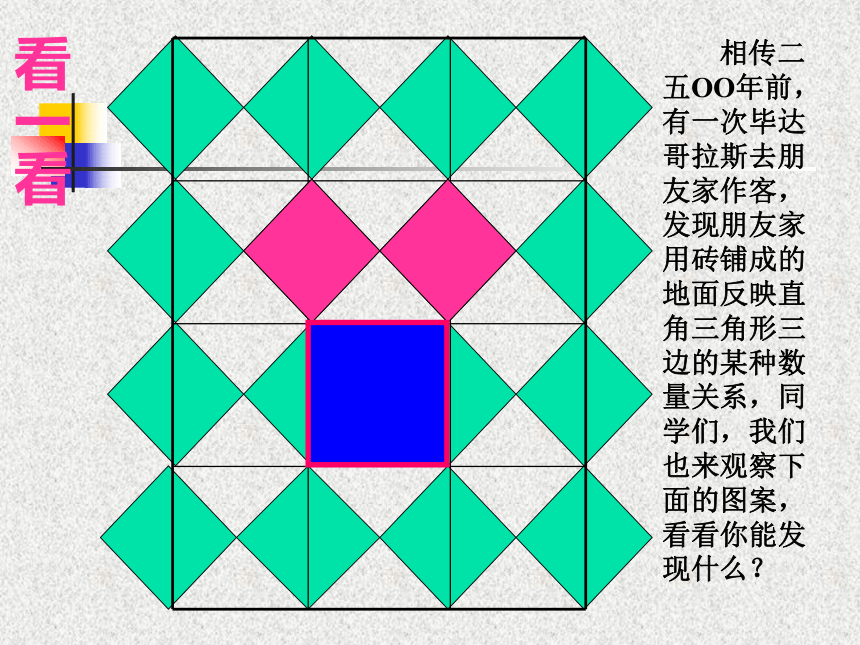
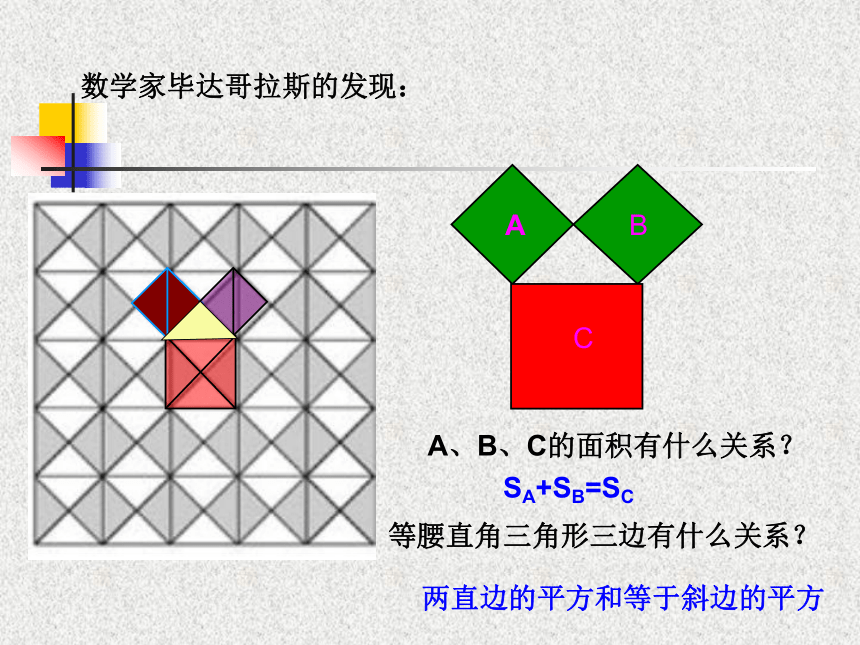
定理:在直角三角形中,斜边大于直角边看一看 相传二五OO年前,有一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么? 数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?等腰直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方(图中每个小方格代表一个单位面积)观察左图
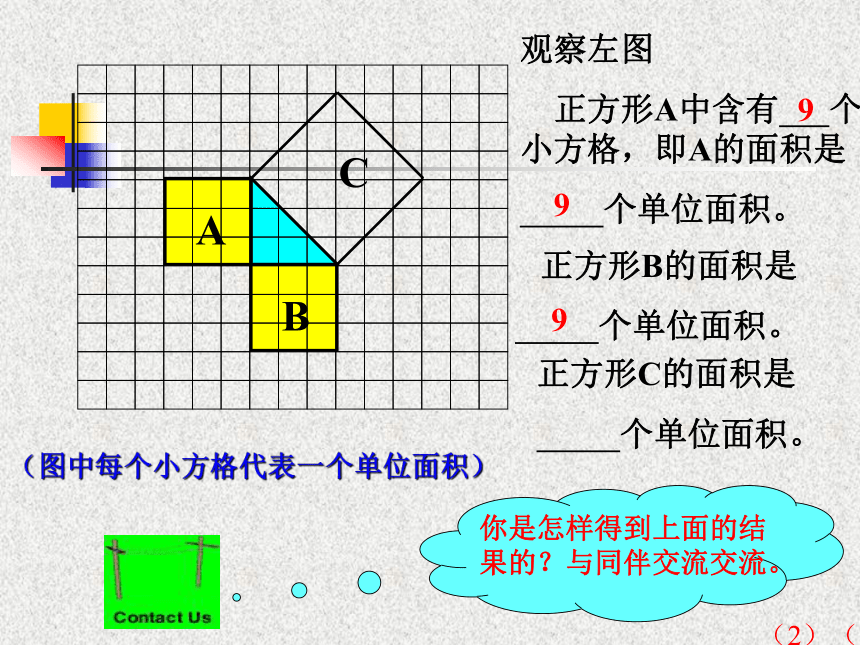
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
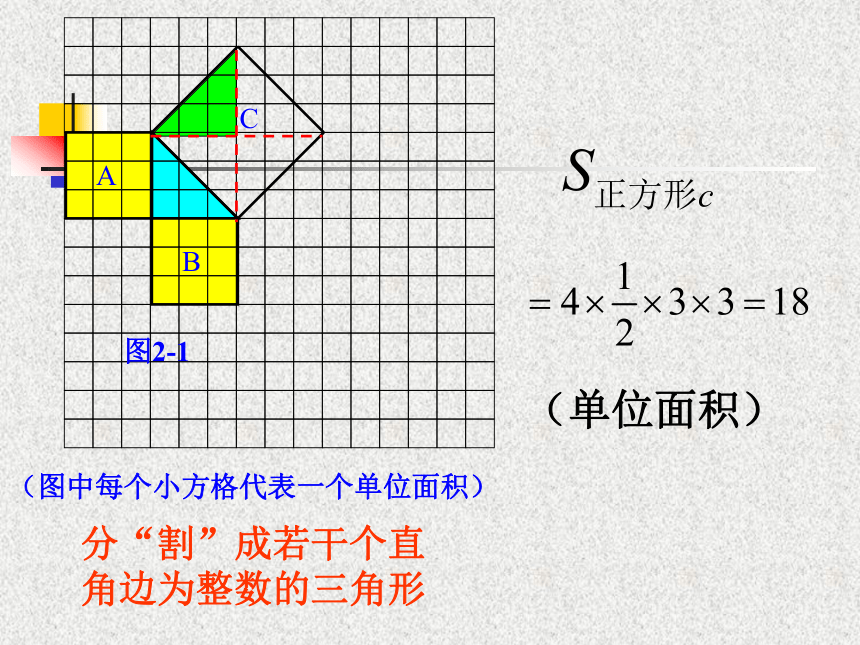
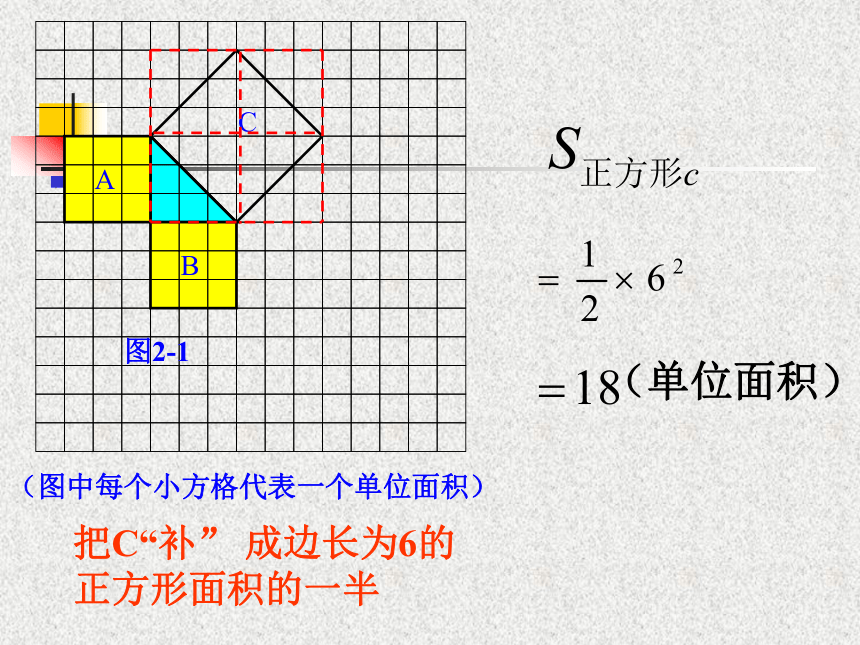
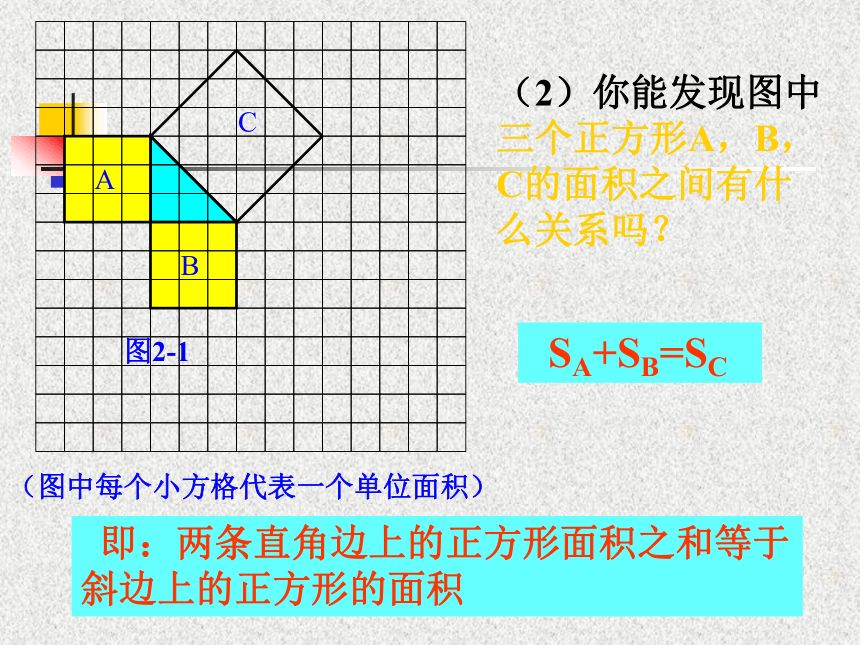
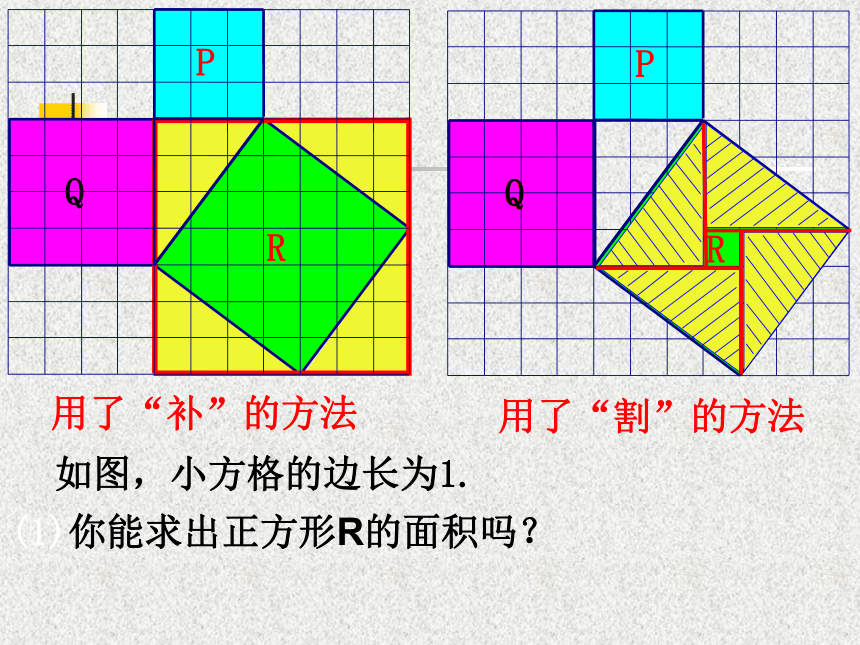
个单位面积。999123(2)(3)(图中每个小方格代表一个单位面积)图2-1分“割”成若干个直角边为整数的三角形(单位面积)(图中每个小方格代表一个单位面积)图2-1(单位面积)把C“补” 成边长为6的正方形面积的一半(图中每个小方格代表一个单位面积)图2-1(2)你能发现图中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积ABC 你认为右图中普通直角三角形三边长度之间还存在上述关系吗?与同伴进行交流。议一议C如图,小方格的边长为1.(1)你能求出正方形R的面积吗?用了“补”的方法用了“割”的方法Q分割成若干个直角边为整数的三角形(面积单位)思考:面积A,B,C还有上述 SA+SB=SC的关系吗?(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。议一议 423252acbSa+Sb=Sc 观察所得到的各组数据,你有什么发现?猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2证明已知:如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.求证:a2+b2=c2.证明 取4个与Rt△ABC全等的直角三角形,把它们拼成如图所示的边长为a+b的正方形EFGH。
可以证明四边形A1B1C1D1是边长为c的正方形(为什么?)。且 S正方形EFGH-4S△ABC=S正方形A1B1C1D1即 (a+b)2-4× ab=c2.化简,得a2+b2=c2.┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。赵爽的弦图毕达哥拉斯的证法思考:大正方形面积怎么求?赵爽弦图所以:大正方形的面积可以表示为 ,又可以表示为 。结论:结论变形 直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b21.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做 例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结 1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C342、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米130120?A3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、125 或 4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .试一试:试一试5、已知Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c= 10,b = 8,则a = .
③若a=2,c=6,则b= 。
6、若一个直角三角形的三边长分别为3,4, x,则x= .
一定要慎重哦! 例2.求边长为1的等边三角形的面积
已知:如图,等边△ABC的边长是 1 .
求S△ABC .例题分析1? 1,已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?议一议:9m24m1046810xEFDCBA8-x8-x课堂小结 与同伴交流下面问题。本节课中我们是如何得到勾股定理的?
又是如何证明勾股定理的?
你还了解哪些关于勾股定理的历史和它的证明方法?作业:一课一练 下节课我们将进一步学习勾股定理的应用,敬请期待。
我们学过直角三角形的哪些性质?我们来进一步研究直角三角形的边所具有的性质问题一
在直角三角形中,直角边与斜边之间有怎样的大小关系?为什么?
定理:在直角三角形中,斜边大于直角边看一看 相传二五OO年前,有一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么? 数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?等腰直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方(图中每个小方格代表一个单位面积)观察左图
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。999123(2)(3)(图中每个小方格代表一个单位面积)图2-1分“割”成若干个直角边为整数的三角形(单位面积)(图中每个小方格代表一个单位面积)图2-1(单位面积)把C“补” 成边长为6的正方形面积的一半(图中每个小方格代表一个单位面积)图2-1(2)你能发现图中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积ABC 你认为右图中普通直角三角形三边长度之间还存在上述关系吗?与同伴进行交流。议一议C如图,小方格的边长为1.(1)你能求出正方形R的面积吗?用了“补”的方法用了“割”的方法Q分割成若干个直角边为整数的三角形(面积单位)思考:面积A,B,C还有上述 SA+SB=SC的关系吗?(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。议一议 423252acbSa+Sb=Sc 观察所得到的各组数据,你有什么发现?猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2证明已知:如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.求证:a2+b2=c2.证明 取4个与Rt△ABC全等的直角三角形,把它们拼成如图所示的边长为a+b的正方形EFGH。
可以证明四边形A1B1C1D1是边长为c的正方形(为什么?)。且 S正方形EFGH-4S△ABC=S正方形A1B1C1D1即 (a+b)2-4× ab=c2.化简,得a2+b2=c2.┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。赵爽的弦图毕达哥拉斯的证法思考:大正方形面积怎么求?赵爽弦图所以:大正方形的面积可以表示为 ,又可以表示为 。结论:结论变形 直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b21.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做 例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结 1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )A.3 米 B.4 米 C.5米 D.6米C342、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米130120?A3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、125 或 4、已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .试一试:试一试5、已知Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c= 10,b = 8,则a = .
③若a=2,c=6,则b= 。
6、若一个直角三角形的三边长分别为3,4, x,则x= .
一定要慎重哦! 例2.求边长为1的等边三角形的面积
已知:如图,等边△ABC的边长是 1 .
求S△ABC .例题分析1? 1,已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?议一议:9m24m1046810xEFDCBA8-x8-x课堂小结 与同伴交流下面问题。本节课中我们是如何得到勾股定理的?
又是如何证明勾股定理的?
你还了解哪些关于勾股定理的历史和它的证明方法?作业:一课一练 下节课我们将进一步学习勾股定理的应用,敬请期待。
