陕西省宁陕县城关初级中学人教版八年级数学上册导学案:12.2 三角形全等的判定(无答案)
文档属性
| 名称 | 陕西省宁陕县城关初级中学人教版八年级数学上册导学案:12.2 三角形全等的判定(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 297.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-04 00:00:00 | ||
图片预览



文档简介
12.2 全等三角形
第二课时(习题课)
复习巩固
全等形、全等三角形的定义。
全等三角形的性质。
习题
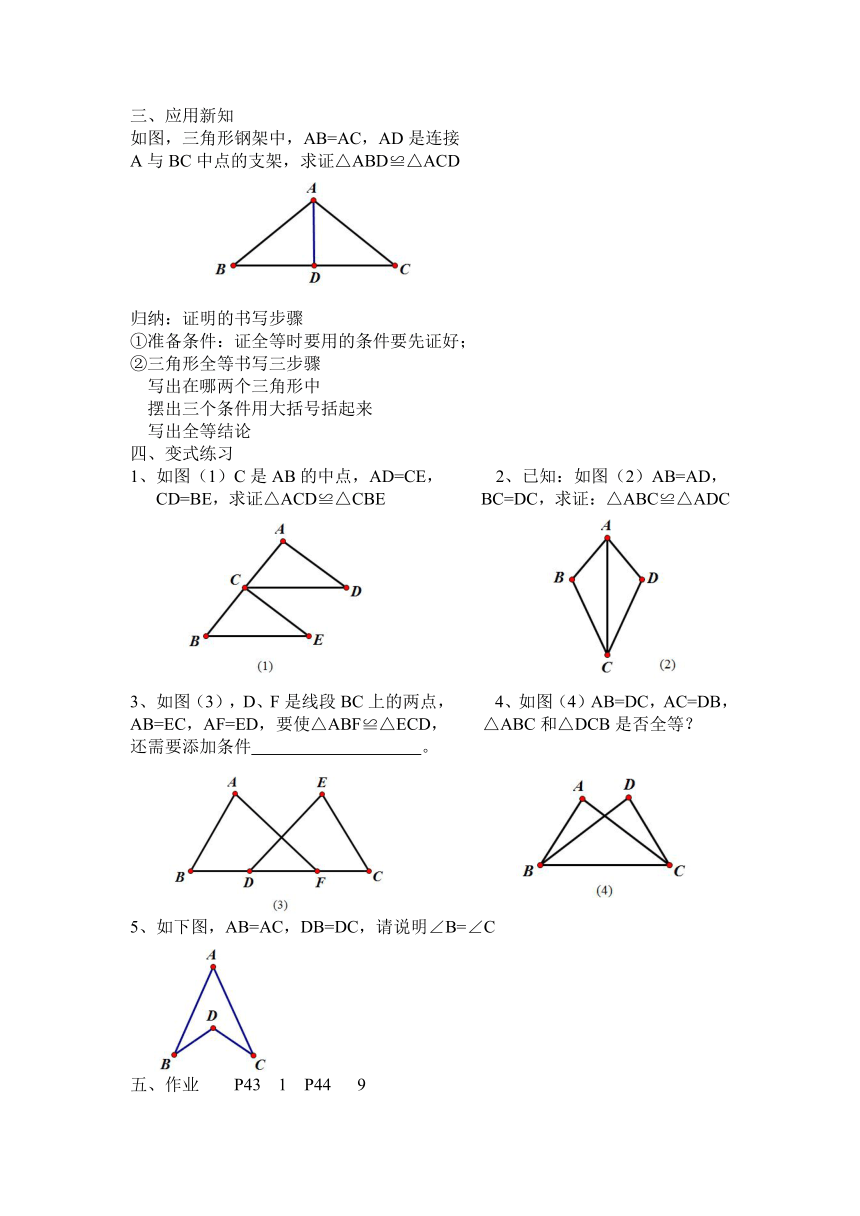
1、下面是两个全等的三角形,按下列图形位置摆放,指出它们的对应顶点,对应边,对应角。
△ABC≌△DEF,BC的对应边是EF,AB=2cm,则DE= cm。
△ABC与△A’B’C’是全等三角形,若AB=A’B’,BC=B’C’,则AC的对应边是 ,∠ACB的对应角是 。
如果△ABC≌△ADC,AB=AD,∠B=70°,BC=3cm,那么∠D= ,DC= cm。
已知下图中的两个三角形全等,则∠α=
如图,已知△ACF≌△DBE,∠E=∠F,
AD=9cm,BC=5cm,求AB的长。
如图
△ABE≌△ACD,∠1=∠2,∠B=∠C,
指出其它的对应边和对应角。
由对应边找对应角,有对应角找对应边
有什么规律?
如图,△ABC≌△ABD,∠DAC=90°
求∠C的度数;
判断AB与CD的位置关系,并说
明理由。
反馈补救
作业 课本P34 6
课后反思
12.2 三角形全等的判定
第一课时
内容:“边边边”判定三角形全等
教学目标:
掌握“边边边”的条件内容。
能初步应用“SSS”条件判定两个三角形全等。
会作一个角等于已知角。
使学生经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
重难点:
重点:“边边边”的条件。
难点:探索三角形全等的条件。
教具准备:直尺、圆规、铅笔。
教学过程:
复习巩固
已知△ABC≌△DEF,找出其中相等的边和角。
思考:
1、满足这六个条件,可以保证△ABC≌△DEF吗?
2、如果只满足这六个条件中的一部分,那么能保
证△ABC≌△DEF吗?
探究新知
(学生分小组完成P35探究1,并分情况进行讨论)
分情况讨论:(要求学生画出符合要求的三角形,同桌相互比较)
只给一个条件
只给一条边 (2)只给一个角
满足两个条件
两边 (2)一边一角 (3)两角
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
满足三个条件
三角 (2)三边 (3)两边一角 (4)两角一边
讨论(1)三角
已知两个三角形的三个内角分别为30°,60°,90°,它们一定全等吗?
(借助手中教具三角尺进行直观演示)
学生分小组完成P35探究2,师巡视指导,生总结探究2的结果反映了什么规律,师补充。
应用新知
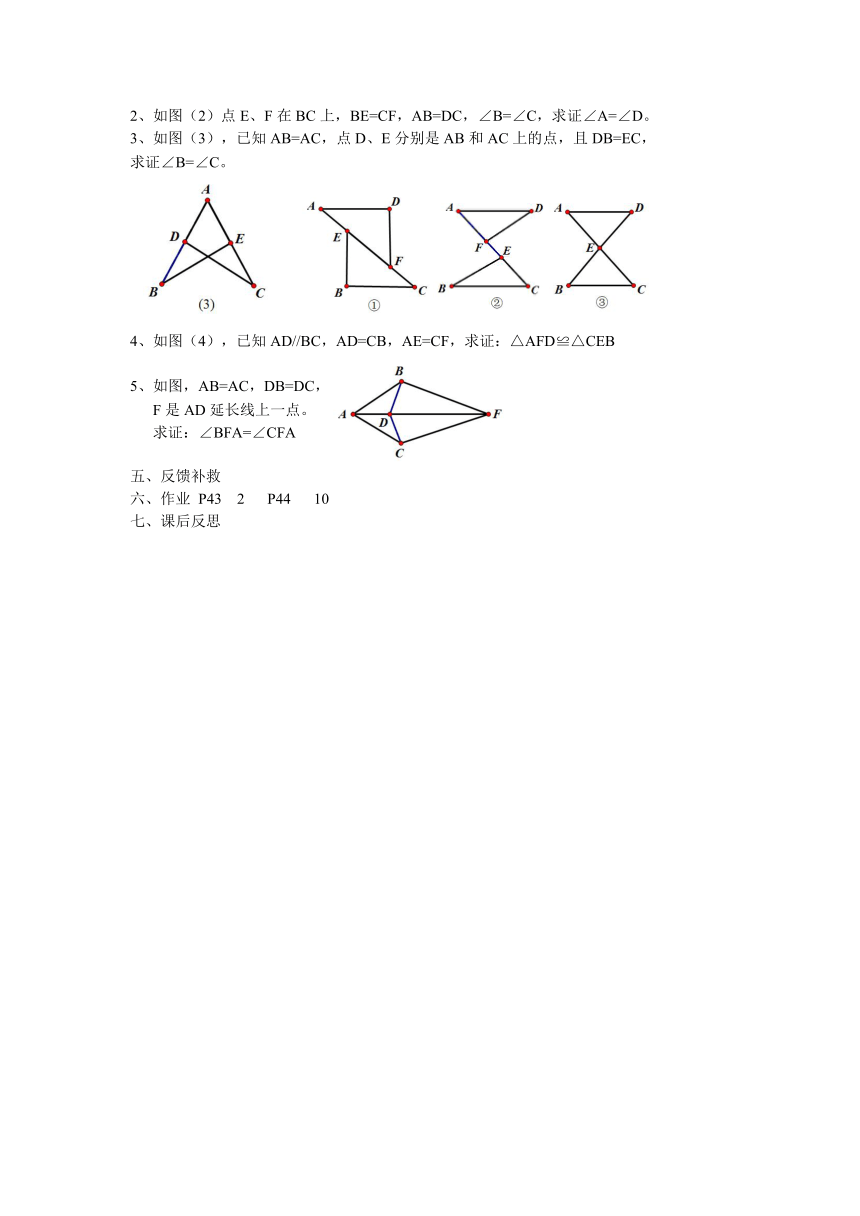
如图,三角形钢架中,AB=AC,AD是连接
A与BC中点的支架,求证△ABD≌△ACD
归纳:证明的书写步骤
①准备条件:证全等时要用的条件要先证好;
②三角形全等书写三步骤
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
变式练习
如图(1)C是AB的中点,AD=CE, 2、已知:如图(2)AB=AD,
CD=BE,求证△ACD≌△CBE BC=DC,求证:△ABC≌△ADC
如图(3),D、F是线段BC上的两点, 4、如图(4)AB=DC,AC=DB,
AB=EC,AF=ED,要使△ABF≌△ECD, △ABC和△DCB是否全等?
还需要添加条件 。
5、如下图,AB=AC,DB=DC,请说明∠B=∠C
五、作业 P43 1 P44 9
12.2 全等三角形的判定
第二课时
“边角边”判定三角形全等
【教学目标】
掌握“SAS”的判定方法。
能初步应用“边角边”条件判定两个三角形全等。
使学生经历探索三角形全等的过程,体验操作,归纳得出数学结论的过程。
【重点】“边角边”条件的理解和应用
【难点】指导学生分析问题,寻找判定三角形全等的条件
【教学准备】多媒体课件、三角板、圆规
【教学过程】
创设情境
上节课学习了三角形全等的判定定理边边边,除此之外,判定三角形全等还有没有其他方法?
探究指导
(生分小组讨论,完成P37探究3,师巡视指导)
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能呢?
注:图一中∠A是AB和AC夹角 图二中 两边和其中一边对角
生总结探究3的结果反映了什么规律?
应用新知
如图:有一池塘,要测池塘两端A,B ( http: / / www.21cnjy.com )的距离,可先在平底上取一点C,从点C不经过池塘可以直接到达点A和点B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE,那么量出DE的长就是A,B的距离,为什么?
变式练习
如图(1)两车从南北方向的路段AB的A端出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?
如图(2)点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证∠A=∠D。
如图(3),已知AB=AC,点D、E分别是AB和AC上的点,且DB=EC,
求证∠B=∠C。
如图(4),已知AD//BC,AD=CB,AE=CF,求证:△AFD≌△CEB
如图,AB=AC,DB=DC,
F是AD延长线上一点。
求证:∠BFA=∠CFA
反馈补救
作业 P43 2 P44 10
课后反思
12.2三角形全等的判定
第三课时
“角边角”和“角角边”判定三角形全等
【教学目标】
掌握“角边角”及“角角边”条件内容。
能初步应用“角边角”及“角角边”条件判定两个三角形全等。
使学生经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
【重点】“角边角”条件及“角角边”条件
【难点】分析问题,寻找判定两个三角形全等的条件
【教学准备】三角板、圆规、多媒体教学
【教学过程】
复习导入
思考我们已经会哪些条件判定两个三角形全等?
探究新知
(多媒体出示教材P39探究4,学生分小组探究讨论,师巡视指导。)
生总结探究4结论,师补充。
思考:师提问,两个角和其中一个角的对边对角相等的两个三角形全等吗?
师出示多媒体:在△ABC和△DEF中,∠A ( http: / / www.21cnjy.com )=∠D,∠B=∠E,BC=EF(如下图),△ABC和△DEF全等吗?你能用角边角证明得到的结论吗?
生分小组讨论证明,师巡视指导,将一个学生的证明过程展台展示, 师生共同纠正,后师生共同总结。
应用新知
如图,点D在AB上,点E在AC上,
AB=AC,∠B=∠C
求证:AD=AE
补充:如图,在△ABC和△DEF中,
∠A=∠D,∠B=∠E,BC=EF。
求证:△ABC≌△DEF
总结:两角和其中一个角的对边分别相等的两个三角形全等(AAS)
变式练习
如图(1)AB⊥BC,AD⊥DC, 2、要测量池塘两岸相对的两点A、B的距离,可以
垂足分别为B、D,∠1=∠2, 在池塘外取AB的垂线BF上的两点C,D,使
求证AB=AD BC=CD,在画出BF的垂线DE,使E与A,C
在一条直线上,这时测得DE的长就是AB的长,
为什么?
如图(3)点D在AB上,点E在AC
上,∠B=∠C,那么补充下列一个条件后,
仍无法判定△ABE≌△ACD
AD=AE B、∠AEB=∠ADC
C、BE=CD D、AB=AC
如图,AB=CD,∠A=∠D,要使
△AEC≌△DFB,还需要增加一个什
么条件?说出增加的条件及理由。
如图,在△ABC中,∠C=2∠B,
AD是△ABC的角平分线,∠1=∠B,
点E在AB边上,求证:AB=AC+CD
反馈补救
作业 课本P44 4,5,11,12
课后反思
12.2 三角形全等的判定
第四课时
“斜边,直角边”判定三角形全等
教学目标:
探索掌握直角三角形全等的条件:“斜边,直角边”。
经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
充分调动学生的积极性,增强学生的自信心。
重难点:
重点:探究直角三角形全等的条件。
难点:灵活运用直角三角形全等的条件进行证明。
教学准备:直尺,圆规
教学过程:
复习巩固
我们已经学过了哪些判定三角形全等的方法?
情境诱导
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
探究新知
师出示多媒体:任意画一个Rt△ABC,使∠C=90°,再画一个Rt△A’B’C’,使∠C’=90°,B’C’=BC,A’B’=AB,把画好的Rt△A’B’C’剪下,放到Rt△ABC上,它们全等吗?
【生分小组讨论P42探究5,师巡视指导,师生共同总结探究5反映的规律】
应用新知
如图,AC⊥BC,BD⊥AD,垂足分
别为C,D,AC=BD
求证:BC=AD
五、变式练习
1、如图(1)C是路段AB的中点,两人从C 2、如图(2),AB=AD,AE⊥BC,
同时出发,以相同的速度分别沿两条直线行走, DF⊥BC,垂足分别为E,F,CE=BF,
并同时到达D、E两地,DA⊥AB,EB⊥AB, 求证:AE=DF
D、E与路段AB的距离相等吗?为什么?
如图(3),点P为∠AOB内一点, 5、 如图(4)AB=AE,BC=ED,∠B=∠E,
PD⊥OA,PE⊥OB,垂足分别为D、E, AF⊥CD,点F为垂足,求证:CF=DF
且PD=PE,猜想:∠AOP与∠BOP有
什么关系?试说明理由。
五、反馈补救
六、作业 1、课本P44 7.8
七、课后反思
三角形全等的判定
第五课时
复习
教学目标
掌握三角形全等的五种判定方法
正确选择恰当的判定方法证明三角形全等
教学过程
复习巩固
△ABC≌△DEF,能得到什么?2、判定三角形全等有哪些方法?
习题
基础练习
1、如图、AB=EF,AC=DE,问 2、如图(1)AC与BD相交于点O,
△ABC≌△EFD吗?为什么? 已知OA=OC,OB=OD。
求证:△AOB≌△COD
已知,如图(2)AB=CB,∠1=∠2, 4、如图(3),AC=BD,∠1=∠2,
△ABD和△CBD全等吗? 求证:BC=AD
变式:如图(2)AB=CB,∠1=∠2 变式:如图(3)AC=BD,BC=AD
求证:(1)AD=CD(2)BD平分∠ADC 求证:∠1=∠2
(3)∠A=∠C
能力提升
如图,已知△ABC≌△A1B1C1,AD, 2、如图,在△ABC中,∠B=∠C,D,
A1D1分别是∠B1C1D1的叫角平分线。 E,F分别在AB,BC,AC上,且
求证:AD=A1D1 BD=CE,∠DEF=∠B,求证:ED=EF
作业 P55 3 P56 8
12.2 三角形全等的判定
第六课时(习题课)
1、如图(1)所示,∠A=∠D,∠1=∠2, 5、如图,AC⊥BE,垂足为C,BD=AE
那么要得到△ABC≌△DEF,还应添加哪 CD=CE,请你探索直线BD与直线
些条件 AE有何位置关系?
如图(2),AE=BE,∠C=∠D,下列结
论不正确的是 ( )
∠DAE=∠CBE B、CE=DE
C、△EBA是等腰三角形
D、△DAE与△CBE面积不同
在△ABC中,∠C=90°,点D是AB边上
一点,DM⊥AB,且DM=AC,过点M作ME//BC
交AB于点E,求证:△ABC≌△MED
如图(4),AB与CD相交于点O,M,N
在AB上,且AC=BD,AM=BN,DM=CN,
请说明AB与CD互相平分。
第二课时(习题课)
复习巩固
全等形、全等三角形的定义。
全等三角形的性质。
习题
1、下面是两个全等的三角形,按下列图形位置摆放,指出它们的对应顶点,对应边,对应角。
△ABC≌△DEF,BC的对应边是EF,AB=2cm,则DE= cm。
△ABC与△A’B’C’是全等三角形,若AB=A’B’,BC=B’C’,则AC的对应边是 ,∠ACB的对应角是 。
如果△ABC≌△ADC,AB=AD,∠B=70°,BC=3cm,那么∠D= ,DC= cm。
已知下图中的两个三角形全等,则∠α=
如图,已知△ACF≌△DBE,∠E=∠F,
AD=9cm,BC=5cm,求AB的长。
如图
△ABE≌△ACD,∠1=∠2,∠B=∠C,
指出其它的对应边和对应角。
由对应边找对应角,有对应角找对应边
有什么规律?
如图,△ABC≌△ABD,∠DAC=90°
求∠C的度数;
判断AB与CD的位置关系,并说
明理由。
反馈补救
作业 课本P34 6
课后反思
12.2 三角形全等的判定
第一课时
内容:“边边边”判定三角形全等
教学目标:
掌握“边边边”的条件内容。
能初步应用“SSS”条件判定两个三角形全等。
会作一个角等于已知角。
使学生经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
重难点:
重点:“边边边”的条件。
难点:探索三角形全等的条件。
教具准备:直尺、圆规、铅笔。
教学过程:
复习巩固
已知△ABC≌△DEF,找出其中相等的边和角。
思考:
1、满足这六个条件,可以保证△ABC≌△DEF吗?
2、如果只满足这六个条件中的一部分,那么能保
证△ABC≌△DEF吗?
探究新知
(学生分小组完成P35探究1,并分情况进行讨论)
分情况讨论:(要求学生画出符合要求的三角形,同桌相互比较)
只给一个条件
只给一条边 (2)只给一个角
满足两个条件
两边 (2)一边一角 (3)两角
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
满足三个条件
三角 (2)三边 (3)两边一角 (4)两角一边
讨论(1)三角
已知两个三角形的三个内角分别为30°,60°,90°,它们一定全等吗?
(借助手中教具三角尺进行直观演示)
学生分小组完成P35探究2,师巡视指导,生总结探究2的结果反映了什么规律,师补充。
应用新知
如图,三角形钢架中,AB=AC,AD是连接
A与BC中点的支架,求证△ABD≌△ACD
归纳:证明的书写步骤
①准备条件:证全等时要用的条件要先证好;
②三角形全等书写三步骤
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
变式练习
如图(1)C是AB的中点,AD=CE, 2、已知:如图(2)AB=AD,
CD=BE,求证△ACD≌△CBE BC=DC,求证:△ABC≌△ADC
如图(3),D、F是线段BC上的两点, 4、如图(4)AB=DC,AC=DB,
AB=EC,AF=ED,要使△ABF≌△ECD, △ABC和△DCB是否全等?
还需要添加条件 。
5、如下图,AB=AC,DB=DC,请说明∠B=∠C
五、作业 P43 1 P44 9
12.2 全等三角形的判定
第二课时
“边角边”判定三角形全等
【教学目标】
掌握“SAS”的判定方法。
能初步应用“边角边”条件判定两个三角形全等。
使学生经历探索三角形全等的过程,体验操作,归纳得出数学结论的过程。
【重点】“边角边”条件的理解和应用
【难点】指导学生分析问题,寻找判定三角形全等的条件
【教学准备】多媒体课件、三角板、圆规
【教学过程】
创设情境
上节课学习了三角形全等的判定定理边边边,除此之外,判定三角形全等还有没有其他方法?
探究指导
(生分小组讨论,完成P37探究3,师巡视指导)
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能呢?
注:图一中∠A是AB和AC夹角 图二中 两边和其中一边对角
生总结探究3的结果反映了什么规律?
应用新知
如图:有一池塘,要测池塘两端A,B ( http: / / www.21cnjy.com )的距离,可先在平底上取一点C,从点C不经过池塘可以直接到达点A和点B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE,那么量出DE的长就是A,B的距离,为什么?
变式练习
如图(1)两车从南北方向的路段AB的A端出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?
如图(2)点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证∠A=∠D。
如图(3),已知AB=AC,点D、E分别是AB和AC上的点,且DB=EC,
求证∠B=∠C。
如图(4),已知AD//BC,AD=CB,AE=CF,求证:△AFD≌△CEB
如图,AB=AC,DB=DC,
F是AD延长线上一点。
求证:∠BFA=∠CFA
反馈补救
作业 P43 2 P44 10
课后反思
12.2三角形全等的判定
第三课时
“角边角”和“角角边”判定三角形全等
【教学目标】
掌握“角边角”及“角角边”条件内容。
能初步应用“角边角”及“角角边”条件判定两个三角形全等。
使学生经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
【重点】“角边角”条件及“角角边”条件
【难点】分析问题,寻找判定两个三角形全等的条件
【教学准备】三角板、圆规、多媒体教学
【教学过程】
复习导入
思考我们已经会哪些条件判定两个三角形全等?
探究新知
(多媒体出示教材P39探究4,学生分小组探究讨论,师巡视指导。)
生总结探究4结论,师补充。
思考:师提问,两个角和其中一个角的对边对角相等的两个三角形全等吗?
师出示多媒体:在△ABC和△DEF中,∠A ( http: / / www.21cnjy.com )=∠D,∠B=∠E,BC=EF(如下图),△ABC和△DEF全等吗?你能用角边角证明得到的结论吗?
生分小组讨论证明,师巡视指导,将一个学生的证明过程展台展示, 师生共同纠正,后师生共同总结。
应用新知
如图,点D在AB上,点E在AC上,
AB=AC,∠B=∠C
求证:AD=AE
补充:如图,在△ABC和△DEF中,
∠A=∠D,∠B=∠E,BC=EF。
求证:△ABC≌△DEF
总结:两角和其中一个角的对边分别相等的两个三角形全等(AAS)
变式练习
如图(1)AB⊥BC,AD⊥DC, 2、要测量池塘两岸相对的两点A、B的距离,可以
垂足分别为B、D,∠1=∠2, 在池塘外取AB的垂线BF上的两点C,D,使
求证AB=AD BC=CD,在画出BF的垂线DE,使E与A,C
在一条直线上,这时测得DE的长就是AB的长,
为什么?
如图(3)点D在AB上,点E在AC
上,∠B=∠C,那么补充下列一个条件后,
仍无法判定△ABE≌△ACD
AD=AE B、∠AEB=∠ADC
C、BE=CD D、AB=AC
如图,AB=CD,∠A=∠D,要使
△AEC≌△DFB,还需要增加一个什
么条件?说出增加的条件及理由。
如图,在△ABC中,∠C=2∠B,
AD是△ABC的角平分线,∠1=∠B,
点E在AB边上,求证:AB=AC+CD
反馈补救
作业 课本P44 4,5,11,12
课后反思
12.2 三角形全等的判定
第四课时
“斜边,直角边”判定三角形全等
教学目标:
探索掌握直角三角形全等的条件:“斜边,直角边”。
经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
充分调动学生的积极性,增强学生的自信心。
重难点:
重点:探究直角三角形全等的条件。
难点:灵活运用直角三角形全等的条件进行证明。
教学准备:直尺,圆规
教学过程:
复习巩固
我们已经学过了哪些判定三角形全等的方法?
情境诱导
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
探究新知
师出示多媒体:任意画一个Rt△ABC,使∠C=90°,再画一个Rt△A’B’C’,使∠C’=90°,B’C’=BC,A’B’=AB,把画好的Rt△A’B’C’剪下,放到Rt△ABC上,它们全等吗?
【生分小组讨论P42探究5,师巡视指导,师生共同总结探究5反映的规律】
应用新知
如图,AC⊥BC,BD⊥AD,垂足分
别为C,D,AC=BD
求证:BC=AD
五、变式练习
1、如图(1)C是路段AB的中点,两人从C 2、如图(2),AB=AD,AE⊥BC,
同时出发,以相同的速度分别沿两条直线行走, DF⊥BC,垂足分别为E,F,CE=BF,
并同时到达D、E两地,DA⊥AB,EB⊥AB, 求证:AE=DF
D、E与路段AB的距离相等吗?为什么?
如图(3),点P为∠AOB内一点, 5、 如图(4)AB=AE,BC=ED,∠B=∠E,
PD⊥OA,PE⊥OB,垂足分别为D、E, AF⊥CD,点F为垂足,求证:CF=DF
且PD=PE,猜想:∠AOP与∠BOP有
什么关系?试说明理由。
五、反馈补救
六、作业 1、课本P44 7.8
七、课后反思
三角形全等的判定
第五课时
复习
教学目标
掌握三角形全等的五种判定方法
正确选择恰当的判定方法证明三角形全等
教学过程
复习巩固
△ABC≌△DEF,能得到什么?2、判定三角形全等有哪些方法?
习题
基础练习
1、如图、AB=EF,AC=DE,问 2、如图(1)AC与BD相交于点O,
△ABC≌△EFD吗?为什么? 已知OA=OC,OB=OD。
求证:△AOB≌△COD
已知,如图(2)AB=CB,∠1=∠2, 4、如图(3),AC=BD,∠1=∠2,
△ABD和△CBD全等吗? 求证:BC=AD
变式:如图(2)AB=CB,∠1=∠2 变式:如图(3)AC=BD,BC=AD
求证:(1)AD=CD(2)BD平分∠ADC 求证:∠1=∠2
(3)∠A=∠C
能力提升
如图,已知△ABC≌△A1B1C1,AD, 2、如图,在△ABC中,∠B=∠C,D,
A1D1分别是∠B1C1D1的叫角平分线。 E,F分别在AB,BC,AC上,且
求证:AD=A1D1 BD=CE,∠DEF=∠B,求证:ED=EF
作业 P55 3 P56 8
12.2 三角形全等的判定
第六课时(习题课)
1、如图(1)所示,∠A=∠D,∠1=∠2, 5、如图,AC⊥BE,垂足为C,BD=AE
那么要得到△ABC≌△DEF,还应添加哪 CD=CE,请你探索直线BD与直线
些条件 AE有何位置关系?
如图(2),AE=BE,∠C=∠D,下列结
论不正确的是 ( )
∠DAE=∠CBE B、CE=DE
C、△EBA是等腰三角形
D、△DAE与△CBE面积不同
在△ABC中,∠C=90°,点D是AB边上
一点,DM⊥AB,且DM=AC,过点M作ME//BC
交AB于点E,求证:△ABC≌△MED
如图(4),AB与CD相交于点O,M,N
在AB上,且AC=BD,AM=BN,DM=CN,
请说明AB与CD互相平分。
