陕西省宁陕县城关初级中学人教版八年级数学上册导学案:13.1 轴对称(无答案)
文档属性
| 名称 | 陕西省宁陕县城关初级中学人教版八年级数学上册导学案:13.1 轴对称(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 146.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-04 08:53:20 | ||
图片预览


文档简介
轴对称
13.1 轴对称
内容:轴对称
教学目标
知识技能:1、理解轴对称图形和两个图形关于某条直线对称的概念。
2、了解轴对称图形的对称轴,两个图形关于某直线对称的对称轴,对应点。
3、掌握线段的垂直平分线的概念。
4、理解和掌握轴对称的性质。
过程与方法:经历观察、操作、实践的过程,发现轴对称图形与两个图形对称轴的性质和特点。
情感态度与价值观:通过对轴对称图形和两个图形成轴对称的学习,激发学生学习的欲望,主动参与数学学习活动。
教学重难点
重点:轴对称图形和两个图形关于某直线对称的概念。
难点:轴对称图形与两个图形关于某直线对称的区别于联系。
教学准备:三角板、剪刀、多媒体课件。
教学过程:
情境导入
展示章前图以及图13.1-1,多媒体课件展示收集到的生活中的图片,让学生欣赏,并初步感知对称图形,请学生列举所见到的类似图形。
(过程中,师需明确轴对称的重要性及本节的探究内容为轴对称的性质)
探究新知
活动一:1、把一张长方形纸对折,剪出一个图案,再打开就能剪出美丽的窗花,你能剪出
什么样的窗花呢?
2、观察剪出的窗花和图13.1-1中的图形,你能发现它们有什么共同特征吗?
3、联系实际,你能举出一个轴对称图形的例子吗?
(师可先示范剪纸,生再动手操作,观察交流后,归纳轴对称图形及对称轴的概念,并板书概念)
活动二、思考:1、教材图13.1-3中,每对图形有什么共同特征?
2、联系实际,你能举出一些生活中两个图形成轴对称的例子吗?你能正确
地完成教材第60页的练习吗?
(学生观察交流,师引导得出两个图形关于某直线堆成及对称轴,对称点的概念,并板书概念)
活动三、1、结合教材图13.1-2和13.1-3进行比较,轴对称图形与两个图形成轴对称有什么
区别?
如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形成轴对称吗?成轴对称
的两个图形全等吗?
如果把一两个成轴对称的图形看成一个整体,它是一个轴对称图形吗?
(学生观察比较,教师引导得出区别)
活动四:1、成轴对称的两个图形全等吗?全等的
两个图形一定成轴对称吗?为什么?
2、在教材图13.1-3中,你能标出
A、B、C的对称点吗?
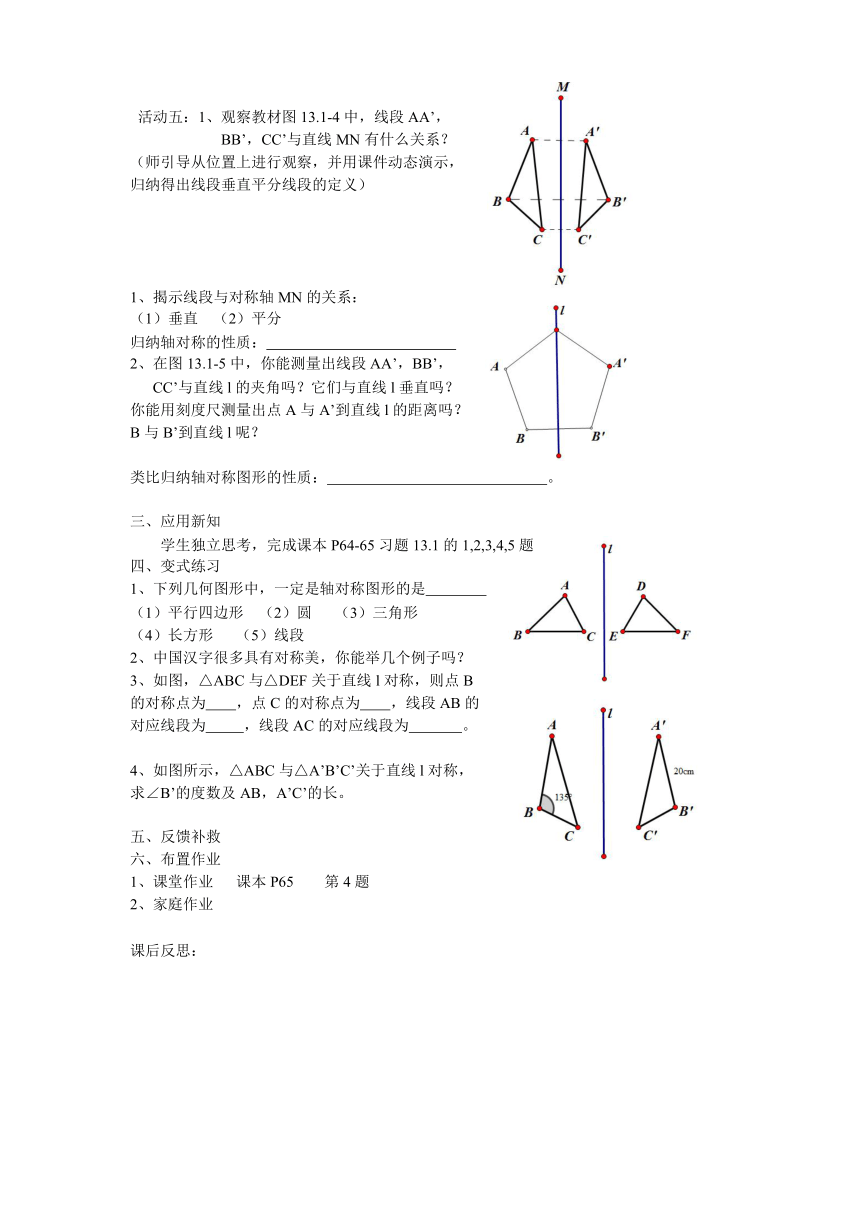
活动五:1、观察教材图13.1-4中,线段AA’,
BB’,CC’与直线MN有什么关系?
(师引导从位置上进行观察,并用课件动态演示,
归纳得出线段垂直平分线段的定义)
1、揭示线段与对称轴MN的关系:
垂直 (2)平分
归纳轴对称的性质:
在图13.1-5中,你能测量出线段AA’,BB’,
CC’与直线l的夹角吗?它们与直线l垂直吗?
你能用刻度尺测量出点A与A’到直线l的距离吗?
B与B’到直线l呢?
类比归纳轴对称图形的性质: 。
应用新知
学生独立思考,完成课本P64-65习题13.1的1,2,3,4,5题
变式练习
下列几何图形中,一定是轴对称图形的是
(1)平行四边形 (2)圆 (3)三角形
(4)长方形 (5)线段
2、中国汉字很多具有对称美,你能举几个例子吗?
3、如图,△ABC与△DEF关于直线l对称,则点B
的对称点为 ,点C的对称点为 ,线段AB的
对应线段为 ,线段AC的对应线段为 。
4、如图所示,△ABC与△A’B’C’关于直线l对称,
求∠B’的度数及AB,A’C’的长。
反馈补救
布置作业
课堂作业 课本P65 第4题
家庭作业
课后反思:
13.1.2 线段垂直平分线的性质(2课时)
第一课时
线段垂直平分线的性质与判定
教学目标:
1、掌握线段的垂直平分线的性质和判定,能灵活运用线段的垂直平分线的性质和判定解题。
2、通过经历线段的垂直平分线的性质与判定的证明过程,体验逻辑推理的数学方法。
3、通过认识上的升华,使学生加深对命题证明的认识。
教学重难点:
重点:线段垂直平分线的性质和判定,能灵活运用线段的垂直平分线的性质和判定解题。
难点:灵活运用线段的垂直平分线的性质和判定解题。
教学准备:三角板 圆规 多媒体课件
教学过程
问题导入
我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴。那么,线段的垂直平分线有什么性质?这节课我们就来研究它。
探究新知
线段的垂直平分线的性质
教师出示教材P61——探究,让学生测量,思考有什么发现?
如图,直线L垂直平分线段AB,P1,P2,P3.......
是L上的点,分别量一量点P1,P2,P3........到点
A与点B的距离,你有什么发现?
(学生回答,教师小结)
线段垂直平分线上的点,与这条线段两端点距离相等。
性质的证明
教师讲解题意并在黑板上绘出图形,明确证明思路。
要求学生自己写出已知,求证并且证明。
(学生完成证明后,师制定一名学生口述证明过程,
师完善并板书供学生对照)
线段的垂直平分线的判定
问题:1、请写出上述性质定理的逆命题。
2、这个命题是真命题吗?如果是,请证明。如果不是,请举出反例。
(学生独立思考,合作交流,师巡视指导)
师生共同完善证明过程,得出结论:
与一条线段两端点距离相等的点,在这条线段的垂直平分线上。
追问:这个判定定理只能判定点在线段的垂直平分线上,那怎么才能判定这条直线就是线段的垂直平分线呢?
尺规作图
经过已知直线外一点作这条直线的垂线。
已知:直线AB和直线AB外一点C
求证:AB的垂线,使它经过点C
作法:
任意取一点K,使点K和点C在AB的两旁。
以点C为圆心,CK长为半径画弧交AB于点D和E。
分别以点D和点E为圆心,大于1/2DE的长为半径作弧,两弧相交于点F。
作直线CF。
应用新知
学生独立思考,完成 P62练习题第1,2题,师巡视指导。
四、变式练习
在△ABC中,AC=16cm,DE为AB 2、如图,在Rt△ABC中,∠A=30°,DE
的垂直平分线,△BCE的周长为26cm, 垂直平分斜边AC,交AB于D,E为垂
求BC的长。 足,连接CD,则∠BDC的度数为 。
如图,点E是∠AOB的平分线上的一
点,EC⊥OA,DE⊥OB,垂足分别是C,D
求证:OE是CD的垂直平分线。 (判定)如图,D在△ABC的边BC上,
且BC=BD+AD,则点D在 的垂直平分线上。
(性质)
如图,直线CD是线段AB的垂直平分 2、在△ABC中,AB=AC=16cm,AB的
线,点P在直线CD上,且PA=5,则线段 垂直平分线ED交AC于E点,垂足为D。
PB= 。 ①当AE=13cm时,求BE
②当△BEC的周长为26cm时,求BC
△ABC,AB=AC,AB的垂直平分线
交AC于P点 五、反馈补救
①∠A=36°,则∠BPC= 。 六、布置作业 课本P65-66 6,9
②若AB=5cm,BC=3cm,则△PBC周长为 。 七、课后反思
第二课时
教学目标:
知识与技能:
会画轴对称图形的对称轴
掌握尺规作图,线段垂直平分线的画法
过程与方法:
通过操作画图,进一步认识轴对称及轴对称的性质。
情感态度与价值观:
通过学习轴对称图形的对称轴的画法,进一步激发学生学习数学的兴趣。
教学重难点:
重点:轴对称图形对称轴的画法尺规作图,作线段中垂线。
难点:掌握作中垂线的方法。
教学准备:三角板 圆规 多媒体课件
教学过程:
问题引入
有时我们感觉两个平面图形是轴对称的,如何验证呢?不折叠图形,你能准确的作出轴对称图形的对称轴吗?
(学生回顾轴对称图形的性质,师适时点拨引导)
探究新知
活动一:
如图,点A,B关于某直线成轴对称,
你能只用圆规和直尺作出这条直线吗?
引导学生思考所作直线与A,B两点的关系,师生共同得出结论。
(学生自学教材P63线段垂直平分线的画法,并在练习本上自己画线段AB的垂直平分线)
师板书“线段垂直平分线”的作法:
分别以点A和点B为圆心,大于1/2AB的长为半径作弧,两弧相交于C,D两点
作直线CD
总结:CD就是线段AB的垂直平分线
活动二:
你能作出∠AOB的对称轴吗? 3、你能把线段AB四等分吗?
(师引导启发,学生自己完成,教师巡视指导)
活动三:
如图,你能画出五角星的对称轴吗?有几条?
教师引导,学生思考
五角星有几条对称轴?
特殊的点是那几个?它们的对称点是哪些?
师生共同得出结论:作轴对称图形的对称轴,即只要找到任意一对对应点,作对应点连线的垂直平分线即可。
新知应用
学生独立思考,完成课本P64练习题1,2,3题
如图,△ABC与△A’B’C’是成轴对称的图形,
画出它们的对称轴。
变式练习
如图,某地由于居民增多,要在公路L 2、如图,A,B,C三点表示三个工厂,
上增加一个公共汽车站,A,B是路边两个 要建一个供水站,使它到这三个工厂的
新建小区,这个公共汽车站建在什么位置, 距离相等,求作供水站的位置P。
能使两个小区到车站的路程一样长?
3、如图,平面上有A,B,C,D四个点,
求作一点P,使PA=PB,PC=PD
反馈补救
课堂小结
作业布置 课本P66 12,13
课后反思:
线段垂直平分线的性质
习题课
一、复习回顾
1、线段垂直平分线的性质
2、线段垂直平分线的判定
3、线段垂直平分线的画法
二、习题练习
1、如图所示,L使线段AB的垂直平 2、如图所示,直线CD是线段AB的
分线则有PA= ,理由 。 垂直平分线,P为直线CD上的一点,
且PA=5,则PB= 。
如图所示,AC=AD,BC=BD,则有 4、三角形ABC中,∠C=90°,AB
AB垂直平分CD 的垂直平分线交AB于点E,交BC于
CD垂直平分AB 点D,若CD:BD=1:2,BC=6cm,则
AB与CD互相垂直平分 点D到点A的距离为 。
CD平分∠ACB
如图所示,在△ABC中,AB=AC=10 6、在△ABC中,∠B=∠C,点P,Q,
DE垂直平分AB,△BEC的周长为17, R分别在AB,BC,AC上,且BP=CQ
求BC的长。 BQ=CR,求证:点Q在PR的垂直平
分线上。
如图所示,在三角形ABC中,AB=AC 8、如图,327国道OA和204国道OB
O是三角形ABC内一点,且OB=OC,试 在某市相交于点O,在∠AOB的内部有
说明:AO⊥BC 工厂C和D,现要修建货站P,使P到
OA,OB距离相等,且使PC=PD,用尺
规作图作出货站P的位置
13.1 轴对称
内容:轴对称
教学目标
知识技能:1、理解轴对称图形和两个图形关于某条直线对称的概念。
2、了解轴对称图形的对称轴,两个图形关于某直线对称的对称轴,对应点。
3、掌握线段的垂直平分线的概念。
4、理解和掌握轴对称的性质。
过程与方法:经历观察、操作、实践的过程,发现轴对称图形与两个图形对称轴的性质和特点。
情感态度与价值观:通过对轴对称图形和两个图形成轴对称的学习,激发学生学习的欲望,主动参与数学学习活动。
教学重难点
重点:轴对称图形和两个图形关于某直线对称的概念。
难点:轴对称图形与两个图形关于某直线对称的区别于联系。
教学准备:三角板、剪刀、多媒体课件。
教学过程:
情境导入
展示章前图以及图13.1-1,多媒体课件展示收集到的生活中的图片,让学生欣赏,并初步感知对称图形,请学生列举所见到的类似图形。
(过程中,师需明确轴对称的重要性及本节的探究内容为轴对称的性质)
探究新知
活动一:1、把一张长方形纸对折,剪出一个图案,再打开就能剪出美丽的窗花,你能剪出
什么样的窗花呢?
2、观察剪出的窗花和图13.1-1中的图形,你能发现它们有什么共同特征吗?
3、联系实际,你能举出一个轴对称图形的例子吗?
(师可先示范剪纸,生再动手操作,观察交流后,归纳轴对称图形及对称轴的概念,并板书概念)
活动二、思考:1、教材图13.1-3中,每对图形有什么共同特征?
2、联系实际,你能举出一些生活中两个图形成轴对称的例子吗?你能正确
地完成教材第60页的练习吗?
(学生观察交流,师引导得出两个图形关于某直线堆成及对称轴,对称点的概念,并板书概念)
活动三、1、结合教材图13.1-2和13.1-3进行比较,轴对称图形与两个图形成轴对称有什么
区别?
如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形成轴对称吗?成轴对称
的两个图形全等吗?
如果把一两个成轴对称的图形看成一个整体,它是一个轴对称图形吗?
(学生观察比较,教师引导得出区别)
活动四:1、成轴对称的两个图形全等吗?全等的
两个图形一定成轴对称吗?为什么?
2、在教材图13.1-3中,你能标出
A、B、C的对称点吗?
活动五:1、观察教材图13.1-4中,线段AA’,
BB’,CC’与直线MN有什么关系?
(师引导从位置上进行观察,并用课件动态演示,
归纳得出线段垂直平分线段的定义)
1、揭示线段与对称轴MN的关系:
垂直 (2)平分
归纳轴对称的性质:
在图13.1-5中,你能测量出线段AA’,BB’,
CC’与直线l的夹角吗?它们与直线l垂直吗?
你能用刻度尺测量出点A与A’到直线l的距离吗?
B与B’到直线l呢?
类比归纳轴对称图形的性质: 。
应用新知
学生独立思考,完成课本P64-65习题13.1的1,2,3,4,5题
变式练习
下列几何图形中,一定是轴对称图形的是
(1)平行四边形 (2)圆 (3)三角形
(4)长方形 (5)线段
2、中国汉字很多具有对称美,你能举几个例子吗?
3、如图,△ABC与△DEF关于直线l对称,则点B
的对称点为 ,点C的对称点为 ,线段AB的
对应线段为 ,线段AC的对应线段为 。
4、如图所示,△ABC与△A’B’C’关于直线l对称,
求∠B’的度数及AB,A’C’的长。
反馈补救
布置作业
课堂作业 课本P65 第4题
家庭作业
课后反思:
13.1.2 线段垂直平分线的性质(2课时)
第一课时
线段垂直平分线的性质与判定
教学目标:
1、掌握线段的垂直平分线的性质和判定,能灵活运用线段的垂直平分线的性质和判定解题。
2、通过经历线段的垂直平分线的性质与判定的证明过程,体验逻辑推理的数学方法。
3、通过认识上的升华,使学生加深对命题证明的认识。
教学重难点:
重点:线段垂直平分线的性质和判定,能灵活运用线段的垂直平分线的性质和判定解题。
难点:灵活运用线段的垂直平分线的性质和判定解题。
教学准备:三角板 圆规 多媒体课件
教学过程
问题导入
我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴。那么,线段的垂直平分线有什么性质?这节课我们就来研究它。
探究新知
线段的垂直平分线的性质
教师出示教材P61——探究,让学生测量,思考有什么发现?
如图,直线L垂直平分线段AB,P1,P2,P3.......
是L上的点,分别量一量点P1,P2,P3........到点
A与点B的距离,你有什么发现?
(学生回答,教师小结)
线段垂直平分线上的点,与这条线段两端点距离相等。
性质的证明
教师讲解题意并在黑板上绘出图形,明确证明思路。
要求学生自己写出已知,求证并且证明。
(学生完成证明后,师制定一名学生口述证明过程,
师完善并板书供学生对照)
线段的垂直平分线的判定
问题:1、请写出上述性质定理的逆命题。
2、这个命题是真命题吗?如果是,请证明。如果不是,请举出反例。
(学生独立思考,合作交流,师巡视指导)
师生共同完善证明过程,得出结论:
与一条线段两端点距离相等的点,在这条线段的垂直平分线上。
追问:这个判定定理只能判定点在线段的垂直平分线上,那怎么才能判定这条直线就是线段的垂直平分线呢?
尺规作图
经过已知直线外一点作这条直线的垂线。
已知:直线AB和直线AB外一点C
求证:AB的垂线,使它经过点C
作法:
任意取一点K,使点K和点C在AB的两旁。
以点C为圆心,CK长为半径画弧交AB于点D和E。
分别以点D和点E为圆心,大于1/2DE的长为半径作弧,两弧相交于点F。
作直线CF。
应用新知
学生独立思考,完成 P62练习题第1,2题,师巡视指导。
四、变式练习
在△ABC中,AC=16cm,DE为AB 2、如图,在Rt△ABC中,∠A=30°,DE
的垂直平分线,△BCE的周长为26cm, 垂直平分斜边AC,交AB于D,E为垂
求BC的长。 足,连接CD,则∠BDC的度数为 。
如图,点E是∠AOB的平分线上的一
点,EC⊥OA,DE⊥OB,垂足分别是C,D
求证:OE是CD的垂直平分线。 (判定)如图,D在△ABC的边BC上,
且BC=BD+AD,则点D在 的垂直平分线上。
(性质)
如图,直线CD是线段AB的垂直平分 2、在△ABC中,AB=AC=16cm,AB的
线,点P在直线CD上,且PA=5,则线段 垂直平分线ED交AC于E点,垂足为D。
PB= 。 ①当AE=13cm时,求BE
②当△BEC的周长为26cm时,求BC
△ABC,AB=AC,AB的垂直平分线
交AC于P点 五、反馈补救
①∠A=36°,则∠BPC= 。 六、布置作业 课本P65-66 6,9
②若AB=5cm,BC=3cm,则△PBC周长为 。 七、课后反思
第二课时
教学目标:
知识与技能:
会画轴对称图形的对称轴
掌握尺规作图,线段垂直平分线的画法
过程与方法:
通过操作画图,进一步认识轴对称及轴对称的性质。
情感态度与价值观:
通过学习轴对称图形的对称轴的画法,进一步激发学生学习数学的兴趣。
教学重难点:
重点:轴对称图形对称轴的画法尺规作图,作线段中垂线。
难点:掌握作中垂线的方法。
教学准备:三角板 圆规 多媒体课件
教学过程:
问题引入
有时我们感觉两个平面图形是轴对称的,如何验证呢?不折叠图形,你能准确的作出轴对称图形的对称轴吗?
(学生回顾轴对称图形的性质,师适时点拨引导)
探究新知
活动一:
如图,点A,B关于某直线成轴对称,
你能只用圆规和直尺作出这条直线吗?
引导学生思考所作直线与A,B两点的关系,师生共同得出结论。
(学生自学教材P63线段垂直平分线的画法,并在练习本上自己画线段AB的垂直平分线)
师板书“线段垂直平分线”的作法:
分别以点A和点B为圆心,大于1/2AB的长为半径作弧,两弧相交于C,D两点
作直线CD
总结:CD就是线段AB的垂直平分线
活动二:
你能作出∠AOB的对称轴吗? 3、你能把线段AB四等分吗?
(师引导启发,学生自己完成,教师巡视指导)
活动三:
如图,你能画出五角星的对称轴吗?有几条?
教师引导,学生思考
五角星有几条对称轴?
特殊的点是那几个?它们的对称点是哪些?
师生共同得出结论:作轴对称图形的对称轴,即只要找到任意一对对应点,作对应点连线的垂直平分线即可。
新知应用
学生独立思考,完成课本P64练习题1,2,3题
如图,△ABC与△A’B’C’是成轴对称的图形,
画出它们的对称轴。
变式练习
如图,某地由于居民增多,要在公路L 2、如图,A,B,C三点表示三个工厂,
上增加一个公共汽车站,A,B是路边两个 要建一个供水站,使它到这三个工厂的
新建小区,这个公共汽车站建在什么位置, 距离相等,求作供水站的位置P。
能使两个小区到车站的路程一样长?
3、如图,平面上有A,B,C,D四个点,
求作一点P,使PA=PB,PC=PD
反馈补救
课堂小结
作业布置 课本P66 12,13
课后反思:
线段垂直平分线的性质
习题课
一、复习回顾
1、线段垂直平分线的性质
2、线段垂直平分线的判定
3、线段垂直平分线的画法
二、习题练习
1、如图所示,L使线段AB的垂直平 2、如图所示,直线CD是线段AB的
分线则有PA= ,理由 。 垂直平分线,P为直线CD上的一点,
且PA=5,则PB= 。
如图所示,AC=AD,BC=BD,则有 4、三角形ABC中,∠C=90°,AB
AB垂直平分CD 的垂直平分线交AB于点E,交BC于
CD垂直平分AB 点D,若CD:BD=1:2,BC=6cm,则
AB与CD互相垂直平分 点D到点A的距离为 。
CD平分∠ACB
如图所示,在△ABC中,AB=AC=10 6、在△ABC中,∠B=∠C,点P,Q,
DE垂直平分AB,△BEC的周长为17, R分别在AB,BC,AC上,且BP=CQ
求BC的长。 BQ=CR,求证:点Q在PR的垂直平
分线上。
如图所示,在三角形ABC中,AB=AC 8、如图,327国道OA和204国道OB
O是三角形ABC内一点,且OB=OC,试 在某市相交于点O,在∠AOB的内部有
说明:AO⊥BC 工厂C和D,现要修建货站P,使P到
OA,OB距离相等,且使PC=PD,用尺
规作图作出货站P的位置
