陕西省宁陕县城关初级中学人教版八年级数学上册导学案:13.4 最短路径问题(无答案)
文档属性
| 名称 | 陕西省宁陕县城关初级中学人教版八年级数学上册导学案:13.4 最短路径问题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 83.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-04 09:11:41 | ||
图片预览

文档简介
最短路径问题
教学目标:
知识与技能:通过对最短路径问题的探索,进一步理解和掌握两点之间线段最短和垂线段最
短。
过程与方法:让学生经历运用所学知识解决问题的过程培养学生解决问题的能力,掌握探索
最短路径问题的思想和方法。
情感态度与价值观:在数学学习活动中获得成功的体验,树立自信心,激发学生的学习兴趣,
让学生感受到数学与现实生活的密切联系。
教学重难点:重点:应用所学知识解决最短路径问题。
难点:选择合理的方法解决问题。
教学准备:三角板
教学过程:
创设情境
思考:①两点的所有连线中, 最短。
②连接直线外一点与直线上各点的所有线段中, 最短。
以上这两个问题,我们称它们为最短路径问题。
下面我们将继续来探讨两个问题,体会如何运用所学知识选择最短路径。
问题探究
探究1:
如图,牧马人从A地出发,到一条笔直的河边L饮马,然后到B地,牧马人到河边,可使所走的路径最短?
提出问题:如果点A和点B分别位于直线的两侧,如何在直线L上找到一点,使得这个点到点A和点B的距离的和最短?
思考:如果点A和点B位于直线的同侧,如何在直线L上找到一点,是的这个店到点A和点B的距离的和最短?
探究2:造桥选址问题
多媒体展示问题2(教材P86)
提出问题:(1)根据问题1 的探讨你对这道题有什么思路和想法?
(2)这个问题有什么不同?
(3)要保证路径AM NB最短,应该怎样选址?
(4)尝试选址作出图形。
新知应用
多媒体出示习题(详见课本)
归纳总结
本节课有什么收获?
布置作业
教材P93 拓广探索 第15题
六、课后反思
轴对称
总复习(第一课时)
一、知识点梳理
1、轴对称与轴对称图形概念及区别。
2、轴对称性质。
3、线段垂直平分线的性质及其判定。
4、线段垂直平分线的尺规作图。
5、画轴对称图形。
6、用坐标表示轴对称。
7、等腰三角形的性质及判定。
8、等边三角形的性质及判定。
9、最短路径问题。
二、巩固练习
1、教材P91-93 复习题13
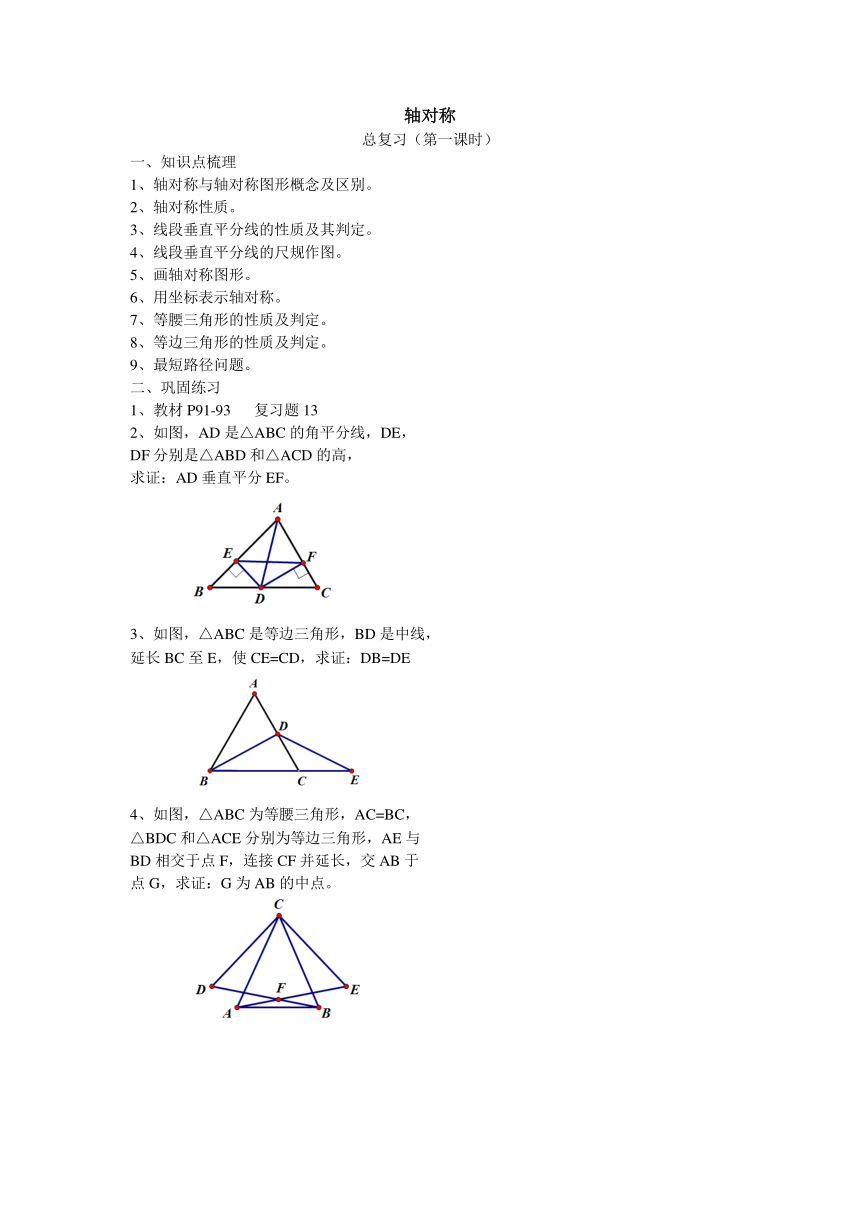
2、如图,AD是△ABC的角平分线,DE,
DF分别是△ABD和△ACD的高,
求证:AD垂直平分EF。
如图,△ABC是等边三角形,BD是中线,
延长BC至E,使CE=CD,求证:DB=DE
如图,△ABC为等腰三角形,AC=BC,
△BDC和△ACE分别为等边三角形,AE与
BD相交于点F,连接CF并延长,交AB于
点G,求证:G为AB的中点。
习题课
(第二课时)
已知,△ABC与△A’B’C’关于直线L对称, 10、△ABC的三个顶点的坐标分别
且∠A=30°,∠C’=75°,则∠B的度数为 。 为A(-2,1),B(-4,2),C(-3,4)
如图,在等腰三角形纸片ABC中,AB=AC, 在平面直角坐标系中画出△ABC,并
∠A=50°,折叠该纸片,使点A落在点B处, 作出△ABC关于y轴的对称图形
折痕为DE,则∠CBE= 。 △A’B’C’ 。
如图所示,在△ABC中,AB=AC,AB的垂直
平分线交AC于点P
若∠A=36°,则∠BPC= ;
若AB=5cm,BC=3cm,则△PBC的周长是 。
点(-1,3)与点(-1,-3)关于 对称,点
(2,-4)关于 对称。
点M(a,-5)与N(-2,b)关于y轴对称,则
a= ,b= 。
一个等腰三角形的两边长分别为3和7,则它的
周长为 。
等腰三角形的一个角是40°,则另外两个角分别
为 。
请画出△ABC关于直线L的对称图形
习题课
(第三课时)
如图,在△ABC中,AB=AC,BD=CF, 6、如图,要在河边L上修建一个泵站,
求证:DF=EF 分别向张庄,李庄送水,水泵应修建在
L的什么位置,可使所用水管最短?试
在图中确定水管的位置。
如图所示,已知,在△ABC中,BC边 7、西安某中学举行文艺晚会,桌子摆
上有D,E两点,∠1=∠2,∠3=∠4 成如图所示两直排,AO桌面上摆满
求证:△ABC是等腰三角形。 了桔子,OB桌面上摆满了糖果,站在
C处的学生小明先拿桔子再拿糖果,
然后到D处座位上,请你帮他设计行
走路线,使其所走的总路程最短?
已知△ABC的三边分别为a,b,c,满
足关系式(a-b)(b-c)(c-a)=0,则这个三角形是
三角形。
如图,在△ABC中,∠C=90°,AC=BC
点D在BC上,且∠BAD=15°
求∠CAD的度数。
若AC=a,BD=b,求AD的长。
如图所示,点E为等边△ABC的边AC上
一点,且∠1=∠2,CD=BE,试判断△ADE
的形状。
教学目标:
知识与技能:通过对最短路径问题的探索,进一步理解和掌握两点之间线段最短和垂线段最
短。
过程与方法:让学生经历运用所学知识解决问题的过程培养学生解决问题的能力,掌握探索
最短路径问题的思想和方法。
情感态度与价值观:在数学学习活动中获得成功的体验,树立自信心,激发学生的学习兴趣,
让学生感受到数学与现实生活的密切联系。
教学重难点:重点:应用所学知识解决最短路径问题。
难点:选择合理的方法解决问题。
教学准备:三角板
教学过程:
创设情境
思考:①两点的所有连线中, 最短。
②连接直线外一点与直线上各点的所有线段中, 最短。
以上这两个问题,我们称它们为最短路径问题。
下面我们将继续来探讨两个问题,体会如何运用所学知识选择最短路径。
问题探究
探究1:
如图,牧马人从A地出发,到一条笔直的河边L饮马,然后到B地,牧马人到河边,可使所走的路径最短?
提出问题:如果点A和点B分别位于直线的两侧,如何在直线L上找到一点,使得这个点到点A和点B的距离的和最短?
思考:如果点A和点B位于直线的同侧,如何在直线L上找到一点,是的这个店到点A和点B的距离的和最短?
探究2:造桥选址问题
多媒体展示问题2(教材P86)
提出问题:(1)根据问题1 的探讨你对这道题有什么思路和想法?
(2)这个问题有什么不同?
(3)要保证路径AM NB最短,应该怎样选址?
(4)尝试选址作出图形。
新知应用
多媒体出示习题(详见课本)
归纳总结
本节课有什么收获?
布置作业
教材P93 拓广探索 第15题
六、课后反思
轴对称
总复习(第一课时)
一、知识点梳理
1、轴对称与轴对称图形概念及区别。
2、轴对称性质。
3、线段垂直平分线的性质及其判定。
4、线段垂直平分线的尺规作图。
5、画轴对称图形。
6、用坐标表示轴对称。
7、等腰三角形的性质及判定。
8、等边三角形的性质及判定。
9、最短路径问题。
二、巩固练习
1、教材P91-93 复习题13
2、如图,AD是△ABC的角平分线,DE,
DF分别是△ABD和△ACD的高,
求证:AD垂直平分EF。
如图,△ABC是等边三角形,BD是中线,
延长BC至E,使CE=CD,求证:DB=DE
如图,△ABC为等腰三角形,AC=BC,
△BDC和△ACE分别为等边三角形,AE与
BD相交于点F,连接CF并延长,交AB于
点G,求证:G为AB的中点。
习题课
(第二课时)
已知,△ABC与△A’B’C’关于直线L对称, 10、△ABC的三个顶点的坐标分别
且∠A=30°,∠C’=75°,则∠B的度数为 。 为A(-2,1),B(-4,2),C(-3,4)
如图,在等腰三角形纸片ABC中,AB=AC, 在平面直角坐标系中画出△ABC,并
∠A=50°,折叠该纸片,使点A落在点B处, 作出△ABC关于y轴的对称图形
折痕为DE,则∠CBE= 。 △A’B’C’ 。
如图所示,在△ABC中,AB=AC,AB的垂直
平分线交AC于点P
若∠A=36°,则∠BPC= ;
若AB=5cm,BC=3cm,则△PBC的周长是 。
点(-1,3)与点(-1,-3)关于 对称,点
(2,-4)关于 对称。
点M(a,-5)与N(-2,b)关于y轴对称,则
a= ,b= 。
一个等腰三角形的两边长分别为3和7,则它的
周长为 。
等腰三角形的一个角是40°,则另外两个角分别
为 。
请画出△ABC关于直线L的对称图形
习题课
(第三课时)
如图,在△ABC中,AB=AC,BD=CF, 6、如图,要在河边L上修建一个泵站,
求证:DF=EF 分别向张庄,李庄送水,水泵应修建在
L的什么位置,可使所用水管最短?试
在图中确定水管的位置。
如图所示,已知,在△ABC中,BC边 7、西安某中学举行文艺晚会,桌子摆
上有D,E两点,∠1=∠2,∠3=∠4 成如图所示两直排,AO桌面上摆满
求证:△ABC是等腰三角形。 了桔子,OB桌面上摆满了糖果,站在
C处的学生小明先拿桔子再拿糖果,
然后到D处座位上,请你帮他设计行
走路线,使其所走的总路程最短?
已知△ABC的三边分别为a,b,c,满
足关系式(a-b)(b-c)(c-a)=0,则这个三角形是
三角形。
如图,在△ABC中,∠C=90°,AC=BC
点D在BC上,且∠BAD=15°
求∠CAD的度数。
若AC=a,BD=b,求AD的长。
如图所示,点E为等边△ABC的边AC上
一点,且∠1=∠2,CD=BE,试判断△ADE
的形状。
