2025中考数学复习冲刺之特色微专题巩固_专题07 各类几何图形面积求解问题(含解析)
文档属性
| 名称 | 2025中考数学复习冲刺之特色微专题巩固_专题07 各类几何图形面积求解问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 15:04:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题07 各类几何图形面积求解问题
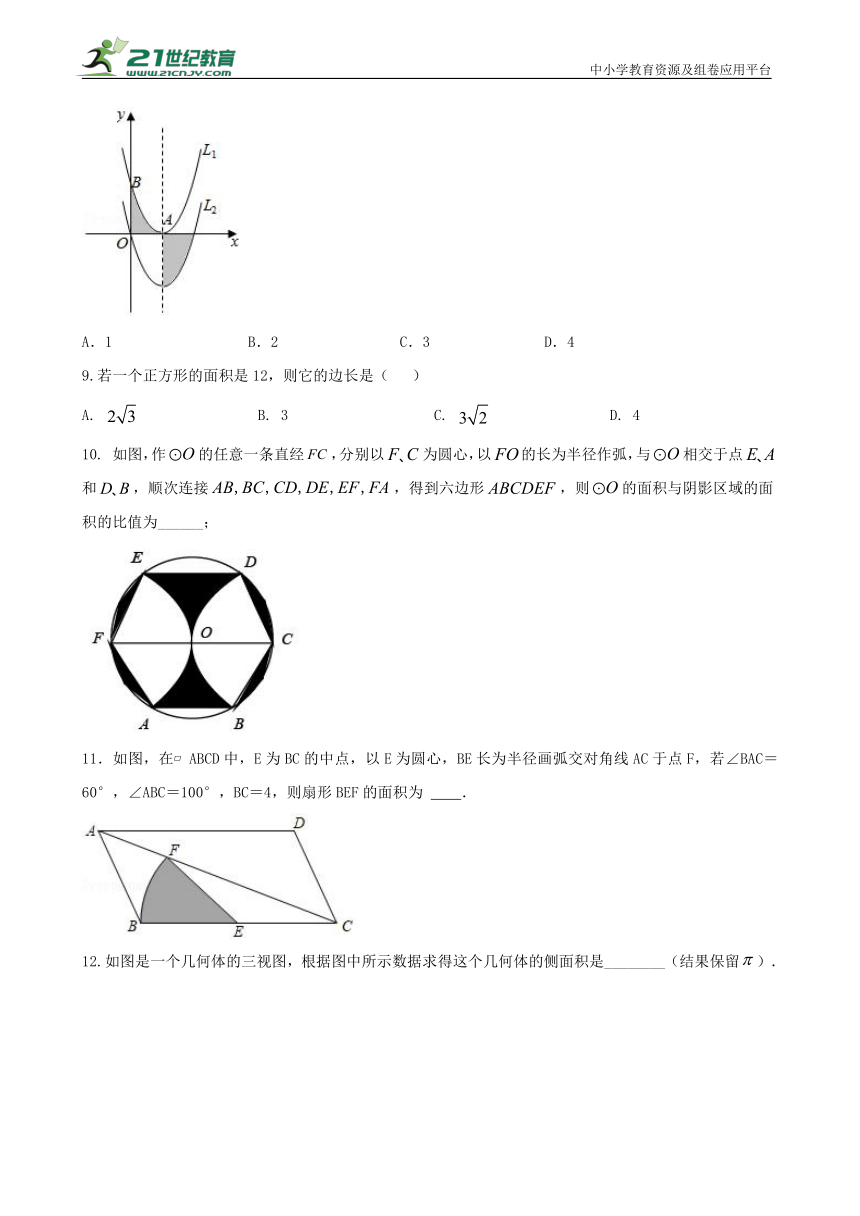
1.中,,D为的中点,,则的面积
为( )
A. B. C. D.
2.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是( )
A.3 B.3 C. D.
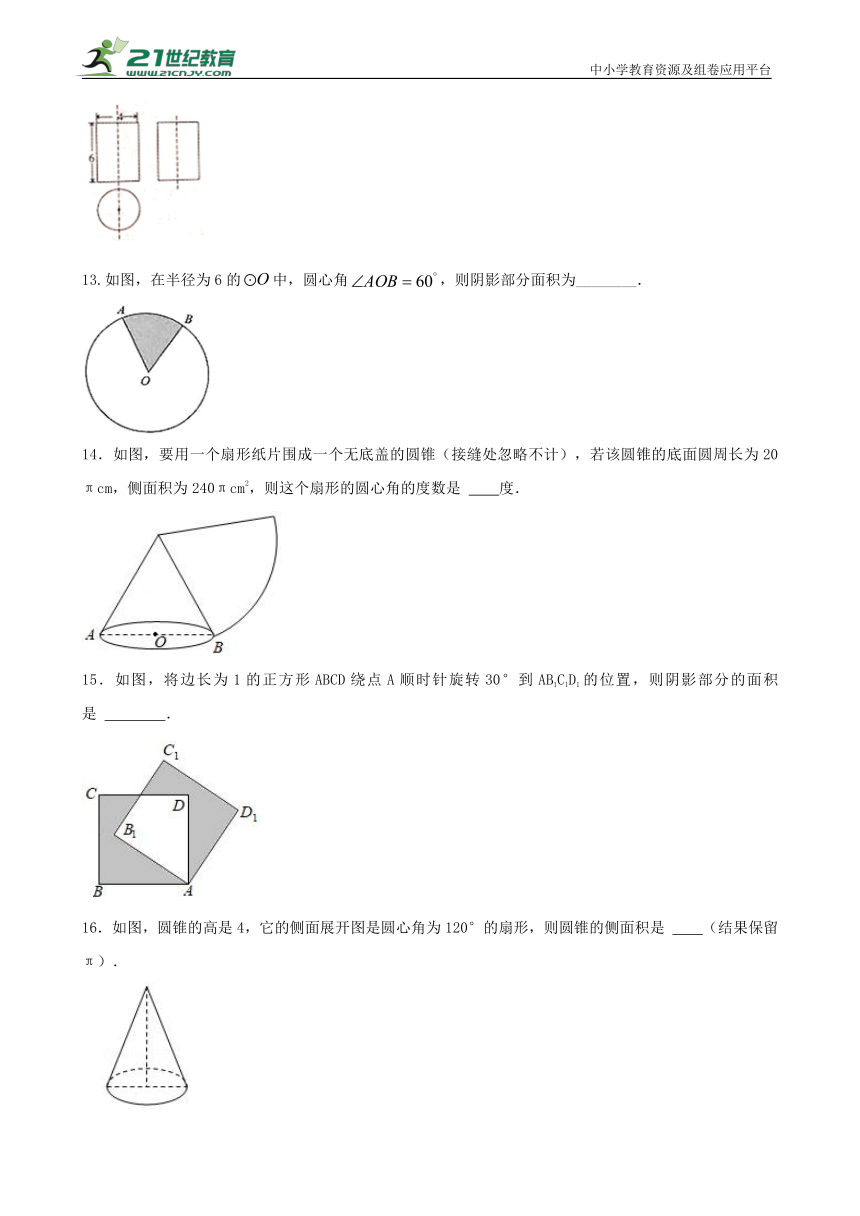
3. 如图,在平行四边形中,,.连接AC,过点B作,交DC的延长线于点E,连接AE,交BC于点F.若,则四边形ABEC的面积为( )
A. B. C. 6 D.
4.如图,在Rt△ABC中,∠ACB=90°,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8﹣π B.4﹣π C.2﹣ D.1﹣
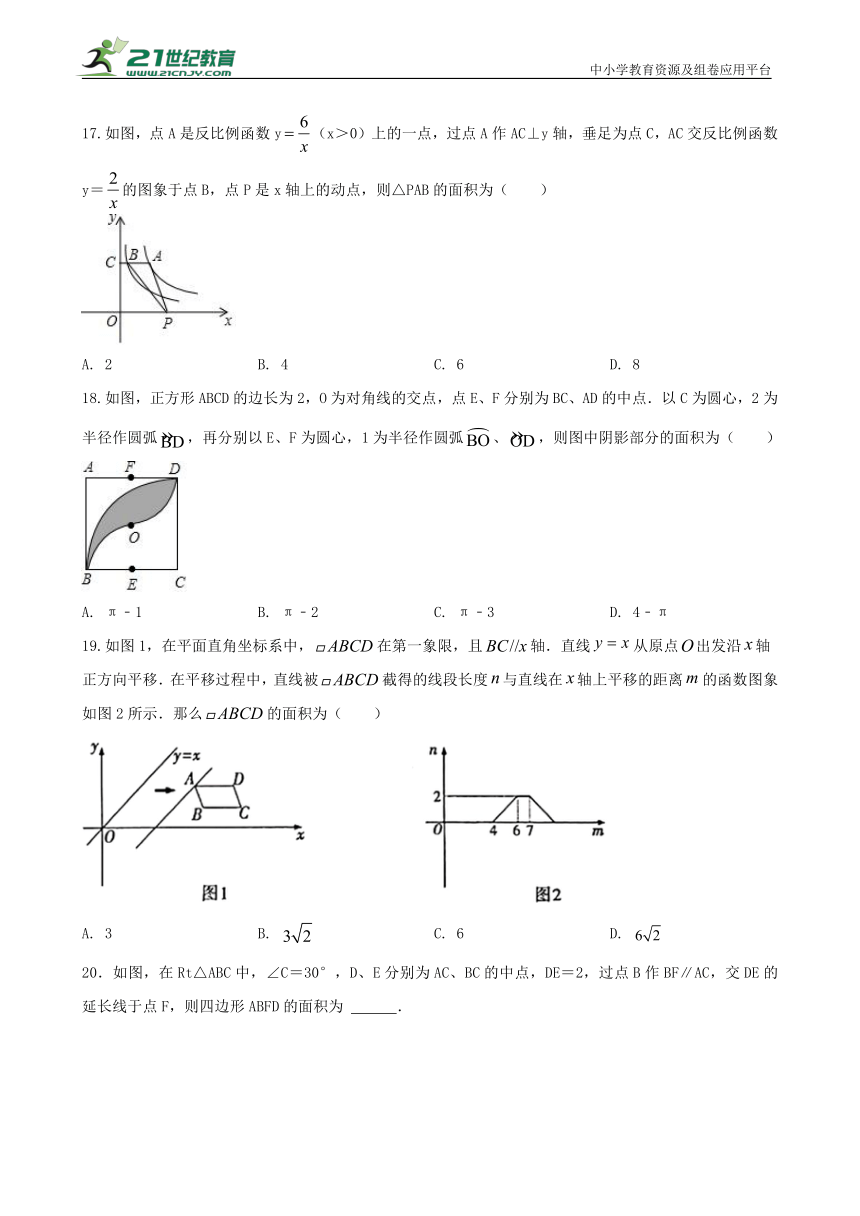
5.如图(1),在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形ABCD的面积为( )
A. B.2 C.8 D.10
6.如图,平行四边形ABFC的对角线AF、BC相交于点E,点O为AC的中点,连接BO并延长,交FC的延长线于点D,交AF于点G,连接AD、OE,若平行四边形ABFC的面积为48,则S△AOG的面积为( )
A.5.5 B.5 C.4 D.3
7.在矩形中,、相交于点,若的面积为2,则矩形的面积为( )
A. 4 B. 6 C. 8 D. 10
8.如图,抛物线L1:y=ax2+bx+c(a≠
0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
9.若一个正方形的面积是12,则它的边长是( )
A. B. 3 C. D. 4
10. 如图,作的任意一条直经,分别以为圆心,以的长为半径作弧,与相交于点和,顺次连接,得到六边形,则的面积与阴影区域的面积的比值为______;
11.如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
12.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________(结果保留).
13.如图,在半径为6的中,圆心角,则阴影部分面积为________.
14.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm2,则这个扇形的圆心角的度数是 度.
15.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置,则阴影部分的面积是 .
16.如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是 (结果保留π).
17.如图,点A是反比例函数y(x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A. 2 B. 4 C. 6 D. 8
18.如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧,再分别以E、F为圆心,1为半径作圆弧、,则图中阴影部分的面积为( )
A. π﹣1 B. π﹣2 C. π﹣3 D. 4﹣π
19.如图1,在平面直角坐标系中,在第一象限,且轴.直线从原点出发沿轴正方向平移.在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图2所示.那么的面积为( )
A. 3 B. C. 6 D.
20.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
21.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
22.如图,△ABC中,∠ABC=90°,AB=2,AC=4,点O为BC的中点,以O为圆心,以OB为半径作半圆,交AC于点D,则图中阴影部分的面积是 .
23.若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
24.如图,从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为 dm2.
25.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 .
26.如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是 .(结果保留π)
27.如图所示的扇形中,,C为上一点,,连接,过C作的垂线交于点D,则图中阴影部分的面积为_______.
28.如图,在中,,点D为AB的中点,以点D为圆心作圆心角为90°的扇形,点C恰好在上,则图中阴影部分的面积为________.
29.如图,已知半圆的直径,点在半圆上,以点为圆心,为半径画弧交于点,连接.若,则图中阴影部分的面积为______.(结果不取近似值)
30.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2、BB2,求△ABB2的面积.
31.如图,半圆的直径AB=6,点C在半圆上,∠BAC=30°,则阴影部分的面积为 (结果保留π).
32.如图,菱形ABCD的边长为4cm,∠A=60°,BD是以点A为圆心,AB长为半径的弧,CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为 cm2.
33.某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
34. 【阅读理解】如图,,的面积与的面积相等吗?为什么?
解:相等在和中,分别作,,垂足分别为E,F.
,
.
,
四边形AEFD是平行四边形,
.
又,.
.
【类比探究】如图,在正方形ABCD的右侧作等腰,,,连接AE,求的面积.
解:过点E作于点F,连接AF.
请将余下的求解步骤补充完整.
【拓展应用】如图,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,,连接BD,BF,DF,直接写出的面积.
35. 如图,在中,于点D,,,,点E是AD上一动点不与点A,D重合,在内作矩形EFGH,点F在DC上,点G,H在AC上,设,连接BE.
(1)当矩形EFGH是正方形时,直接写出EF的长;
(2)设的面积为,矩形EFGH的面积为,令,求y关于x的函数解析式不要求写出自变量x的取值范围;
(3)如图,点是中得到的函数图象上的任意一点,过点P的直线l分别与x轴正半轴,y轴正半轴交于M,N两点,求面积的最小值,并说明理由.
专题07 各类几何图形面积求解问题(解析版)
1.中,,D为的中点,,则的面积
为( )
A. B. C. D.
【答案】B
【解析】连接AD,用等腰三角形的“三线合一”,得到的度数,及,由得,得,计算的面积即可.
连接AD,如图所示:
∵,且D为BC中点
∴,且,
∴中,
∵
∴
∴
故选:B.
【点睛】考查等腰三角形的性质,及解直角三角形和三角形面积的计算,熟知以上知识是解题的关键.
2.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是( )
A.3 B.3 C. D.
【答案】D
【解析】取AC中点O,连接OP,BO,由勾股定理的逆定理可求∠APC=90°,可得点P在以AC为直径的圆上运动,由三角形的三边关系可得BP≥BO﹣OP,当点P在线段BO上时,BP有最小值,由锐角三角函数可求∠BOC=60°,即可求解.
解:取AC中点O,连接OP,BO,
∵PA2+PC2=AC2,
∴∠APC=90°,
∴点P在以AC为直径的圆上运动,
在△BPO中,BP≥BO﹣OP,
∴当点P在线段BO上时,BP有最小值,
∵点O是AC的中点,∠APC=90°,
∴PO=AO=CO=,
∵tan∠BOC==,
∴∠BOC=60°,
∴△COP是等边三角形,
∴S△COP=OC2=×3=,
∵OA=OC,
∴△ACP的面积=2S△COP=,
故选:D.
3. 如图,在平行四边形中,,.连接AC,过点B作,交DC的延长线于点E,连接AE,交BC于点F.若,则四边形ABEC的面积为( )
A. B. C. 6 D.
【答案】B
【解析】先证明四边形ABEC为矩形,再求出AC,即可求出四边形ABEC的面积.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=2,BC=AD=3,∠D=∠ABC,
∵,
∴四边形ABEC为平行四边形,
∵,
∴,
∵∠AFC=∠ABF+∠BAF,
∴∠ABF=∠BAF,
∴AF=BF,
∴2AF=2BF,
即BC=AE,
∴平行四边形ABEC是矩形,
∴∠BAC=90°,
∴,
∴矩形ABEC的面积为.
【点睛】本题考查了平行四边形的性质,矩形的判定与性质,勾股定理等知识,熟知相关定理,证明四边形ABEC为矩形是解题关键.
4.如图,在Rt△ABC中,∠ACB=90°,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8﹣π B.4﹣π C.2﹣ D.1﹣
【答案】D
【解析】先根据直角三角形中的勾股定理求得AC=1,再将求不规则的阴影部分面积转化为求规则图形的面积:S阴影部分=S△ABC﹣(S扇形EBF+S扇形DAC),将相关量代入求解即可.
解:根据题意可知AC===1,则BE=BE=AD=AC=1,
设∠B=n°,∠A=m°,
∵∠ACB=90°,
∴∠B+∠A=90°,即n+m=90,
∴S阴影部分=S△ABC﹣(S扇形EBF+S扇形DAC)=﹣()=1﹣=1﹣,
5.如图(1),在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形ABCD的面积为( )
A. B.2 C.8 D.10
【答案】C
【解析】根据函数图象中的数据可以分别求得矩形的边长BC,AB的长,从而可以求得矩形的面积.
如图所示,过点B、D分别作y=2x+1的平行线,交AD、BC于点E、F.
由图象和题意可得AE=4﹣3=1,CF=8﹣7=1,BE=DF=,BF=DE=7﹣4=3,
则AB===2,BC=BF+CF=3+1=4,
∴矩形ABCD的面积为AB BC=2×4=8.
6.如图,平行四边形ABFC的对角线AF、BC相交于点E,点O为AC的中点,连接BO并延长,交FC的延长线于点D,交AF于点G,连接AD、OE,若平行四边形ABFC的面积为48,则S△AOG的面积为( )
A.5.5 B.5 C.4 D.3
【答案】C
【分析】利用平行四边形ABFC的对角线AF、BC相交于点E,可得BE=CE,即点E为BC的中点,由于点O为AC的中点,所以OE为△ABC的中位线,可得OE∥AB,且OE=AB;利用OE∥AB可得,进而得出;利用高相等的三角形的面积比等于它们底的比可得;利用AO=OC,可得,利用△ABC≌△FCB,可得,答案可得.
解:∵四边形ABFC是平行四边形,
∴BE=EC.
∵OA=OC,
∴OE是△ABC的中位线.
∴OE=AB,OE∥AB.
∴.
∴.
∴,
∵AO=OC,
∴,
∵四边形ABFC是平行四边形,
∴FC=AB,FB=AC.
在△ABC和△FCB中,
,
∴△ABC≌△FCB(SSS).
∴S△ABC=S△FCB==24.
∴==4.
7.在矩形中,、相交于点,若的面积为2,则矩形的面积为( )
A. 4 B. 6 C. 8 D. 10
【答案】C
【解析】根据矩形的性质得到OA=OB=OC=OD,推出,即可求出矩形ABCD的面积.
∵四边形ABCD是矩形,对角线、相交于点,
∴AC=BD,且OA=OB=OC=OD,
∴,
∴矩形的面积为,
故选:C
【点睛】此题考查矩形的性质:矩形的对角线相等,且互相平分,由此可以将矩形的;面积四等分,由此可以解决问题,熟记矩形的性质定理是解题的关键.
8.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】根据题意可推出OB=2,OA=1,AD=OC=2,根据平移的性质及抛物线的对称性可知阴影部分的面积等于矩形OCDA的面积,利用矩形的面积公式进行求解即可.
如图所示,
过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,
则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),
∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA AD=1×2=2.
9.若一个正方形的面积是12,则它的边长是( )
A. B. 3 C. D. 4
【答案】A
【解析】根据正方形的面积公式即可求解.
由题意知:正方形的面积等于边长×边长,设边长为a,
故a =12,
∴a=±,又边长大于0
∴边长a=.
故选:A.
【点睛】本题考查了正方形的面积公式,开平方运算等,属于基础题.
10. 如图,作的任意一条直经,分别以为圆心,以的长为半径作弧,与相交于点和,顺次连接,得到六边形,则的面积与阴影区域的面积的比值为______;
【答案】
【解析】可将图中阴影部分的面积转化为两个等边三角形的面积之和,设⊙O的半径与等边三角形的边长为,分别表示出圆的面积和两个等边三角形的面积,即可求解
【详解】连接,,,,
由题可得:
为边长相等的等边三角形
可将图中阴影部分的面积转化为和的面积之和,如图所示:
设⊙O的半径与等边三角形的边长为,
⊙O的面积为
等边与等边的边长为
⊙O的面积与阴影部分的面积比为.
【点睛】本题考查了图形的面积转换,等边三角形面积以及圆面积的求法,将不规则图形的面积转换成规则图形的面积是解题关键.
11.如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
【答案】.
【解析】根据三角形内角和定理求出∠ACB,根据三角形的外角的性质求出∠BEF,根据扇形面积公式计算.
∵∠BAC=60°,∠ABC=100°,
∴∠ACB=20°,
又∵E为BC的中点,
∴BE=EC=BC=2,
∵BE=EF,
∴EF=EC=2,
∴∠EFC=∠ACB=20°,
∴∠BEF=40°,
∴扇形BEF的面积==
12.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________(结果保留).
【答案】24π cm
【解析】根据三视图确定该几何体是圆柱体,再计算圆柱体的侧面积.
【详解】解:先由三视图确定该几何体是圆柱体,底面半径是4÷2=2cm,高是6cm,
圆柱的侧面展开图是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,
且底面周长为:2π×2=4π(cm),
∴这个圆柱的侧面积是4π×6=24π(cm ).
故答案为:24π cm .
【点睛】主要考查由三视图确定几何体和求圆柱体的侧面积,关键是根据三视图确定该几何体是圆柱体.
13.如图,在半径为6的中,圆心角,则阴影部分面积为________.
【答案】
【解析】直接根据扇形的面积计算公式计算即可.
阴影部分面积为,
故答案为:.
【点睛】本题考查了扇形面积的计算,解题的关键是熟记扇形面积的计算公式.
14.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm2,则这个扇形的圆心角的度数是 度.
【答案】150
【解析】根据扇形面积公式求出圆锥的母线长,再根据弧长公式计算,得到答案.
设圆锥的母线长为lcm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20πcm,
∴圆锥的侧面展开图扇形的弧长为20πcm,
由题意得:×20π×l=240π,
解得:l=24,
则=20π,
解得,n=150,即扇形的圆心角为150°.
15.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置,则阴影部分的面积是 .
【答案】2﹣.
【解析】连接AE,根据旋转的性质推出Rt△AB1E≌Rt△ADE,再由含30度角的直角三角形性质得出DE=,最后由图可以得出S阴影部分=2(S正方形ABCD﹣S四边形ADEB1),将相关数值代入求解即可.如图,
连接AE,根据题意可知AB1=AD=1,∠B1=∠D=90°,∠BAB1=30°,
在Rt△AB1E和Rt△ADE中,
,
∴Rt△AB1E≌Rt△ADE(HL),
∵∠B1AE=∠DAE=∠B1AD=30°,
∴=,解得DE=,
∴S四边形ADEB1=2S△ADE=2××AD×DE=,
∴S阴影部分=2(S正方形ABCD﹣S四边形ADEB1)=2×(1﹣)=2﹣.
16.如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是 (结果保留π).
【答案】6π.
【解析】设圆锥的底面半径为r,母线长为l,根据题意得:2πr=,解得:l=3r,然后根据高为4,利用勾股定理得r2+42=(3r)2,从而求得底面半径和母线长,利用侧面积公式求得答案即可.
【解答】解:设圆锥的底面半径为r,母线长为l,
根据题意得:2πr=,
解得:l=3r,
∵高为4,
∴r2+42=(3r)2,
解得:r=,
∴母线长为3,
∴圆锥的侧面积为πrl=π××3=6π.
17.如图,点A是反比例函数y(x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A. 2 B. 4 C. 6 D. 8
【答案】A
【解析】连接OA、OB、PC.由于AC⊥y轴,根据三角形的面积公式以及反比例函数比例系数k的几何意义得到S△APC=S△AOC=3,S△BPC=S△BOC=1,然后利用S△PAB=S△APC﹣S△APB进行计算.
如图,
连接OA、OB、PC.
∵AC⊥y轴,
∴S△APC=S△AOC=×|6|=3,S△BPC=S△BOC=×|2|=1,
∴S△PAB=S△APC﹣S△BPC=2.
故选:A.
【点睛】本题考查了反比例函数的比例系数k的几何意义:在反比例函数图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
18.如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧,再分别以E、F为圆心,1为半径作圆弧、,则图中阴影部分的面积为( )
A. π﹣1 B. π﹣2 C. π﹣3 D. 4﹣π
【答案】B
【解析】根据题意和图形,可知阴影部分的面积是以2为半径的四分之一个圆(扇形)的面积减去以1为半径的半圆(扇形)的面积再减去2个以边长为1的正方形的面积减去以1半径的四分之一个圆(扇形)的面积,本题得以解决.
由题意可得,
阴影部分的面积是: π×22﹣﹣2(1×1﹣ π×12)=π﹣2,
故选:B.
【点睛】主要考查运用正方形的性质,圆的面积公式(或扇形的面积公式),正方形的面积公式计算不规则几何图形的面积,解题的关键是理解题意,观察图形,合理分割,转化为规则图形的面积和差进行计算.
19.如图1,在平面直角坐标系中,在第一象限,且轴.直线从原点出发沿轴正方向平移.在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图2所示.那么的面积为( )
A. 3 B. C. 6 D.
【答案】B
【解析】根据图象可以得到当移动的距离是4时,直线经过点A;当移动距离是6时,直线经过B,在移动距离是7时经过D,则AD=7-4=3,当直线经过D点,设交BC与N.则DN=2,作DM⊥AB于点M.利用三角函数即可求得DM即平行四边形的高,然后利用平行四边形的面积公式即可求解.
【详解】根据图象可以得到当移动的距离是4时,直线经过点A
当移动距离是6时,直线经过B
当移动距离是7时经过D,则AD=7-4=3
如图:设交BC与N,则DN=2,作DM⊥AB于点M,
∵移动直线为y=x
∴∠NDM=45°
∴DM=cos∠NDM·ND=
∴的面积为AD×DM=3×=3.
故答案为B.
【点睛】本题考查了平移变换、解直角三角形等知识,其中根据平移变换确定AD的长是解答本题的关键.
20.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
【答案】8.
【解析】由三角形的中位线定理证得DE∥AB,AB=2DE=4,进而证得四边形ABFD是平行四边形,在Rt△ABC中,根据勾股定理求出BC=4,得到BE=2,根据平行四边形的面积公式即可求出四边形ABFD的面积.
∵D、E分别为AC、BC的中点,
∵DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴AB=2DE,DF∥AB,
又∵BF∥AC,
∴BF∥AD,
∴四边形ABFD是平行四边形,
∵AB⊥BE,
∴S平行四边形ABFD=AB BE,
∵DE=2,
∴AB=2×2=4,
在Rt△ABC中,
∵∠C=30°,
∴AC=2AB=2×4=8,
∴BC===4,
∴BE=BC=2,
∴S平行四边形ABFD=4×2=8,故答案为8.
21.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
【答案】1:3.
【解析】通过证明△AEM∽△ABC,可得,可求EF的长,由相似三角形的性质可得=()2=,即可求解.
∵四边形EFGH和四边形HGNM均为正方形,
∴EF=EH=HM,EM∥BC,
∴△AEM∽△ABC,
∴,
∴,
∴EF=,
∴EM=5,
∵△AEM∽△ABC,
∴=()2=,
∴S四边形BCME=S△ABC﹣S△AEM=3S△AEM,
∴△AEM与四边形BCME的面积比为1:3,故答案为:1:3.
22.如图,△ABC中,∠ABC=90°,AB=2,AC=4,点O为BC的中点,以O为圆心,以OB为半径作半圆,交AC于点D,则图中阴影部分的面积是 .
【答案】﹣.
【解析】根据题意,作出合适的辅助线,即可求得DE的长、∠
DOB的度数,然后根据图形可知阴影部分的面积是△ABC的面积减去△COD的面积和扇形BOD的面积,从而可以解答本题.
连接OD,过D作DE⊥BC于E,
在△ABC中,∠ABC=90°,AB=2,AC=4,
∴sinC===,BC===2,
∴∠C=30°,
∴∠DOB=60°,
∵OD=BC=,
∴DE=,
∴阴影部分的面积是:2×2﹣﹣=﹣,
故答案为:﹣.
23.若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
【答案】4.
【解析】连接CD.构建直径所对的圆周角∠BDC=90°,然后利用等腰直角△ABC的性质:斜边上的中线是斜边的一半、中线与垂线重合,求得CD=BD=AD,从而求得弦BD与CD所对的弓形的面积相等,所以图中阴影部分的面积=直角三角形ABC的面积﹣直角三角形BCD的面积.
解:连接CD.
∵BC是直径,
∴∠BDC=90°,即CD⊥AB;
又∵△ABC为等腰直角三角形,
∴CD是斜边AB的垂直平分线,
∴CD=BD=AD,
∴=,
∴S弓形BD=S弓形CD,
∴S阴影=SRt△ABC﹣SRt△BCD;
∵△ABC为等腰直角三角形,CD是斜边AB的垂直平分线,
∴SRt△ABC=2SRt△BCD;
又SRt△ABC=×4×4=8,
∴S阴影=4.
24.如图,从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为 dm2.
【答案】2π.
【解析】连接AC,根据圆周角定理得出AC为圆的直径,解直角三角形求出AB,根据扇形面积公式求出即可.
连接AC,
∵从一块直径为4dm的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,
∴AC为直径,即AC=4dm,AB=BC(扇形的半径相等),
∵AB2+BC2=22,
∴AB=BC=2dm,
∴阴影部分的面积是=2π(dm2).
25.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 .
【答案】6
【解析】过A作AH⊥OC,过B作BG⊥OC,根据已知条件结合反比例函数k的几何意义,求出点A与点B的坐标关系,再确定△ACH与△AOH的面积.
解:过A作AH⊥OC,过B作BG⊥OC,
∵A、B两点在反比例函数y=﹣(x<0)的图象上,
∴设A(x,﹣),S△AOH=,
∵AB=2BC,
∴,,
∴BG=AH,HG=2CG
∴点B的纵坐标为,代反比例函数中得点B的坐标为(3x,),
∴OG=﹣3x,HG=﹣2x,CG=﹣x,则OC=﹣4x,
∴S△AOC== (﹣4x) (﹣)=6
26.如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是 .(结果保留π)
【答案】π﹣.
【解析】由∠C=45°根据圆周角定理得出∠AOB=90°,根据S阴影=S扇形AOB﹣S△AOB可得出结论.
∵∠C=45°,
∴∠AOB=90°,
∴S阴影=S扇形AOB﹣S△AOB
=
=π﹣.
27.如图所示的扇形中,,C为上一点,,连接,过C作的垂线交于点D,则图中阴影部分的面积为_______.
【答案】
【解析】先根据题目条件计算出OD,CD的长度,判断为等边三角形,之后表示出阴影面积的计算公式进行计算即可.
在中,
∴
∵
∴
∵
∴为等边三角形
∴
故答案为:
【点睛】本题考查了阴影面积的计算,熟知不规则阴影面积的计算方法是解题的关键.
28.如图,在中,,点D为AB的中点,以点D为圆心作圆心角为90°的扇形,点C恰好在上,则图中阴影部分的面积为________.
【答案】
【解析】如解图,连接,过点作于点,于点.
设交于点,交于点,
,,点为的中点,,,
,四边形是正方形,,
则,
,
,
在和中,,
,
,
.
29.如图,已知半圆的直径,点在半圆上,以点为圆心,为半径画弧交于点,连接.若,则图中阴影部分的面积为______.(结果不取近似值)
【答案】
【解析】根据60°特殊角求出AC和BC,再算出△ABC的面积,根据扇形面积公式求出扇形的面积,再用三角形的面积减去扇形面积即可.
【详解】∵AB是直径,
∴∠ACB=90°,∠ABC=60°,
∴BC=,AC=,
∴,
由以上可知∠CAB=30°,
∴扇形ACD的面积=,
∴阴影部分的面积为.
30.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2、BB2,求△ABB2的面积.
【答案】见解析。
【解析】(1)根据网格结构找出点A1、B1的位置,然后顺次连接即可;
(2)根据网格结构找出点B2的位置,然后连接即可;
(3)利用正方形的面积减去三个三角形的面积,列式计算即可得解.
解:(1)线段A1B1如图所示;
(2)线段A1B2如图所示;
(3)S=4×4﹣×2×2﹣×2×4﹣×2×4=6.
【点拨】本题考查了平移变换和旋转变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
31.如图,半圆的直径AB=6,点C在半圆上,∠BAC=30°,则阴影部分的面积为 (结果保留π).
【答案】3π﹣.
【解析】根据题意,作出合适的辅助线,即可求得CD和∠COB的度数,即可得到阴影部分的面积是半圆的面积减去△AOC和扇形BOC的面积.
连接OC、BC,作CD⊥AB于点D,
∵直径AB=6,点C在半圆上,∠BAC=30°,
∴∠ACB=90°,∠COB=60°,
∴AC=3,
∵∠CDA=90°,
∴CD=,
∴阴影部分的面积是:=3π﹣
【点评】本题考查扇形面积的计算、圆周角定理,解答本题的关键是明确题意,利用数形结合的思想解答.
32.如图,菱形ABCD的边长为4cm,∠A=60°,BD是以点A为圆心,AB长为半径的弧,CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为 cm2.
【答案】4.
【解析】连接BD,判断出△ABD是等边三角形,根据等边三角形的性质可得∠ABD=60°,再求出∠CBD=60°,然后求出阴影部分的面积=S△ABD,计算即可得解.
如图,连接BD,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠ABD=60°,
又∵菱形的对边AD∥BC,
∴∠ABC=180°﹣60°=120°,
∴∠CBD=120°﹣60°=60°,
∴S阴影=S扇形BDC﹣(S扇形ABD﹣S△ABD),
=S△ABD,
=×4×=4cm2.
故答案为:4.
33.某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
【答案】见解析。
【解析】(1)设∠BAC=n°.根据弧EF的两种求法,构建方程,可得结论.
(2)根据S阴= BC AD﹣S扇形AEF求解即可.
解:(1)设∠BAC=n°.
由题意得π DE=,AD=2DE,
∴n=90,∴∠BAC=90°.
(2)∵AD=2DE=10(cm),
∴S阴= BC AD﹣S扇形AEF=×10×20﹣=(100﹣25π)cm2.
34. 【阅读理解】如图,,的面积与的面积相等吗?为什么?
解:相等在和中,分别作,,垂足分别为E,F.
,
.
,
四边形AEFD是平行四边形,
.
又,.
.
【类比探究】如图,在正方形ABCD的右侧作等腰,,,连接AE,求的面积.
解:过点E作于点F,连接AF.
请将余下的求解步骤补充完整.
【拓展应用】如图,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,,连接BD,BF,DF,直接写出的面积.
【答案】见解析。
【解析】【类比探究】由等腰三角形的性质可得,,可证,可得,由三角形的面积公式可求解;
【拓展应用】连接CF,由正方形的性质可得,可得,可得,由三角形的面积公式可求解.
本题是四边形综合题,考查了正方形的性质,等腰三角形的性质,三角形面积公式等知识,能掌握和运用“阅读理解”中的知识是解题的关键.
【类比探究】过点E作于点F,连接AF,
四边形ABCD是正方形,
,,
,,
,,
,
,
;
【拓展应用】如图,连接CF,
四边形ABCD和四边形CGFE都是正方形,
,,
,
,
,
.
35. 如图,在中,于点D,,,,点E是AD上一动点不与点A,D重合,在内作矩形EFGH,点F在DC上,点G,H在AC上,设,连接BE.
(1)当矩形EFGH是正方形时,直接写出EF的长;
(2)设的面积为,矩形EFGH的面积为,令,求y关于x的函数解析式不要求写出自变量x的取值范围;
(3)如图,点是中得到的函数图象上的任意一点,过点P的直线l分别与x轴正半轴,y轴正半轴交于M,N两点,求面积的最小值,并说明理由.
【答案】见解析。
【解析】设.
,,
,
,
,
,
,
,
四边形EFGH是正方形,
,,
,
,
,,
,,
,
,
.
,,
,
,,
,
.
如图中,由可知点P在上,
当OP最小时,点P在第一象限的角平分线时,此时,
当直线时,的面积最小,
此时,
的面积的最小值.
专题07 各类几何图形面积求解问题
1.中,,D为的中点,,则的面积
为( )
A. B. C. D.
2.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是( )
A.3 B.3 C. D.
3. 如图,在平行四边形中,,.连接AC,过点B作,交DC的延长线于点E,连接AE,交BC于点F.若,则四边形ABEC的面积为( )
A. B. C. 6 D.
4.如图,在Rt△ABC中,∠ACB=90°,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8﹣π B.4﹣π C.2﹣ D.1﹣
5.如图(1),在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形ABCD的面积为( )
A. B.2 C.8 D.10
6.如图,平行四边形ABFC的对角线AF、BC相交于点E,点O为AC的中点,连接BO并延长,交FC的延长线于点D,交AF于点G,连接AD、OE,若平行四边形ABFC的面积为48,则S△AOG的面积为( )
A.5.5 B.5 C.4 D.3
7.在矩形中,、相交于点,若的面积为2,则矩形的面积为( )
A. 4 B. 6 C. 8 D. 10
8.如图,抛物线L1:y=ax2+bx+c(a≠
0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
9.若一个正方形的面积是12,则它的边长是( )
A. B. 3 C. D. 4
10. 如图,作的任意一条直经,分别以为圆心,以的长为半径作弧,与相交于点和,顺次连接,得到六边形,则的面积与阴影区域的面积的比值为______;
11.如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
12.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________(结果保留).
13.如图,在半径为6的中,圆心角,则阴影部分面积为________.
14.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm2,则这个扇形的圆心角的度数是 度.
15.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置,则阴影部分的面积是 .
16.如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是 (结果保留π).
17.如图,点A是反比例函数y(x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A. 2 B. 4 C. 6 D. 8
18.如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧,再分别以E、F为圆心,1为半径作圆弧、,则图中阴影部分的面积为( )
A. π﹣1 B. π﹣2 C. π﹣3 D. 4﹣π
19.如图1,在平面直角坐标系中,在第一象限,且轴.直线从原点出发沿轴正方向平移.在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图2所示.那么的面积为( )
A. 3 B. C. 6 D.
20.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
21.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
22.如图,△ABC中,∠ABC=90°,AB=2,AC=4,点O为BC的中点,以O为圆心,以OB为半径作半圆,交AC于点D,则图中阴影部分的面积是 .
23.若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
24.如图,从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为 dm2.
25.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 .
26.如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是 .(结果保留π)
27.如图所示的扇形中,,C为上一点,,连接,过C作的垂线交于点D,则图中阴影部分的面积为_______.
28.如图,在中,,点D为AB的中点,以点D为圆心作圆心角为90°的扇形,点C恰好在上,则图中阴影部分的面积为________.
29.如图,已知半圆的直径,点在半圆上,以点为圆心,为半径画弧交于点,连接.若,则图中阴影部分的面积为______.(结果不取近似值)
30.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2、BB2,求△ABB2的面积.
31.如图,半圆的直径AB=6,点C在半圆上,∠BAC=30°,则阴影部分的面积为 (结果保留π).
32.如图,菱形ABCD的边长为4cm,∠A=60°,BD是以点A为圆心,AB长为半径的弧,CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为 cm2.
33.某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
34. 【阅读理解】如图,,的面积与的面积相等吗?为什么?
解:相等在和中,分别作,,垂足分别为E,F.
,
.
,
四边形AEFD是平行四边形,
.
又,.
.
【类比探究】如图,在正方形ABCD的右侧作等腰,,,连接AE,求的面积.
解:过点E作于点F,连接AF.
请将余下的求解步骤补充完整.
【拓展应用】如图,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,,连接BD,BF,DF,直接写出的面积.
35. 如图,在中,于点D,,,,点E是AD上一动点不与点A,D重合,在内作矩形EFGH,点F在DC上,点G,H在AC上,设,连接BE.
(1)当矩形EFGH是正方形时,直接写出EF的长;
(2)设的面积为,矩形EFGH的面积为,令,求y关于x的函数解析式不要求写出自变量x的取值范围;
(3)如图,点是中得到的函数图象上的任意一点,过点P的直线l分别与x轴正半轴,y轴正半轴交于M,N两点,求面积的最小值,并说明理由.
专题07 各类几何图形面积求解问题(解析版)
1.中,,D为的中点,,则的面积
为( )
A. B. C. D.
【答案】B
【解析】连接AD,用等腰三角形的“三线合一”,得到的度数,及,由得,得,计算的面积即可.
连接AD,如图所示:
∵,且D为BC中点
∴,且,
∴中,
∵
∴
∴
故选:B.
【点睛】考查等腰三角形的性质,及解直角三角形和三角形面积的计算,熟知以上知识是解题的关键.
2.如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是( )
A.3 B.3 C. D.
【答案】D
【解析】取AC中点O,连接OP,BO,由勾股定理的逆定理可求∠APC=90°,可得点P在以AC为直径的圆上运动,由三角形的三边关系可得BP≥BO﹣OP,当点P在线段BO上时,BP有最小值,由锐角三角函数可求∠BOC=60°,即可求解.
解:取AC中点O,连接OP,BO,
∵PA2+PC2=AC2,
∴∠APC=90°,
∴点P在以AC为直径的圆上运动,
在△BPO中,BP≥BO﹣OP,
∴当点P在线段BO上时,BP有最小值,
∵点O是AC的中点,∠APC=90°,
∴PO=AO=CO=,
∵tan∠BOC==,
∴∠BOC=60°,
∴△COP是等边三角形,
∴S△COP=OC2=×3=,
∵OA=OC,
∴△ACP的面积=2S△COP=,
故选:D.
3. 如图,在平行四边形中,,.连接AC,过点B作,交DC的延长线于点E,连接AE,交BC于点F.若,则四边形ABEC的面积为( )
A. B. C. 6 D.
【答案】B
【解析】先证明四边形ABEC为矩形,再求出AC,即可求出四边形ABEC的面积.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=2,BC=AD=3,∠D=∠ABC,
∵,
∴四边形ABEC为平行四边形,
∵,
∴,
∵∠AFC=∠ABF+∠BAF,
∴∠ABF=∠BAF,
∴AF=BF,
∴2AF=2BF,
即BC=AE,
∴平行四边形ABEC是矩形,
∴∠BAC=90°,
∴,
∴矩形ABEC的面积为.
【点睛】本题考查了平行四边形的性质,矩形的判定与性质,勾股定理等知识,熟知相关定理,证明四边形ABEC为矩形是解题关键.
4.如图,在Rt△ABC中,∠ACB=90°,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8﹣π B.4﹣π C.2﹣ D.1﹣
【答案】D
【解析】先根据直角三角形中的勾股定理求得AC=1,再将求不规则的阴影部分面积转化为求规则图形的面积:S阴影部分=S△ABC﹣(S扇形EBF+S扇形DAC),将相关量代入求解即可.
解:根据题意可知AC===1,则BE=BE=AD=AC=1,
设∠B=n°,∠A=m°,
∵∠ACB=90°,
∴∠B+∠A=90°,即n+m=90,
∴S阴影部分=S△ABC﹣(S扇形EBF+S扇形DAC)=﹣()=1﹣=1﹣,
5.如图(1),在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形ABCD的面积为( )
A. B.2 C.8 D.10
【答案】C
【解析】根据函数图象中的数据可以分别求得矩形的边长BC,AB的长,从而可以求得矩形的面积.
如图所示,过点B、D分别作y=2x+1的平行线,交AD、BC于点E、F.
由图象和题意可得AE=4﹣3=1,CF=8﹣7=1,BE=DF=,BF=DE=7﹣4=3,
则AB===2,BC=BF+CF=3+1=4,
∴矩形ABCD的面积为AB BC=2×4=8.
6.如图,平行四边形ABFC的对角线AF、BC相交于点E,点O为AC的中点,连接BO并延长,交FC的延长线于点D,交AF于点G,连接AD、OE,若平行四边形ABFC的面积为48,则S△AOG的面积为( )
A.5.5 B.5 C.4 D.3
【答案】C
【分析】利用平行四边形ABFC的对角线AF、BC相交于点E,可得BE=CE,即点E为BC的中点,由于点O为AC的中点,所以OE为△ABC的中位线,可得OE∥AB,且OE=AB;利用OE∥AB可得,进而得出;利用高相等的三角形的面积比等于它们底的比可得;利用AO=OC,可得,利用△ABC≌△FCB,可得,答案可得.
解:∵四边形ABFC是平行四边形,
∴BE=EC.
∵OA=OC,
∴OE是△ABC的中位线.
∴OE=AB,OE∥AB.
∴.
∴.
∴,
∵AO=OC,
∴,
∵四边形ABFC是平行四边形,
∴FC=AB,FB=AC.
在△ABC和△FCB中,
,
∴△ABC≌△FCB(SSS).
∴S△ABC=S△FCB==24.
∴==4.
7.在矩形中,、相交于点,若的面积为2,则矩形的面积为( )
A. 4 B. 6 C. 8 D. 10
【答案】C
【解析】根据矩形的性质得到OA=OB=OC=OD,推出,即可求出矩形ABCD的面积.
∵四边形ABCD是矩形,对角线、相交于点,
∴AC=BD,且OA=OB=OC=OD,
∴,
∴矩形的面积为,
故选:C
【点睛】此题考查矩形的性质:矩形的对角线相等,且互相平分,由此可以将矩形的;面积四等分,由此可以解决问题,熟记矩形的性质定理是解题的关键.
8.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】根据题意可推出OB=2,OA=1,AD=OC=2,根据平移的性质及抛物线的对称性可知阴影部分的面积等于矩形OCDA的面积,利用矩形的面积公式进行求解即可.
如图所示,
过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,
则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),
∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA AD=1×2=2.
9.若一个正方形的面积是12,则它的边长是( )
A. B. 3 C. D. 4
【答案】A
【解析】根据正方形的面积公式即可求解.
由题意知:正方形的面积等于边长×边长,设边长为a,
故a =12,
∴a=±,又边长大于0
∴边长a=.
故选:A.
【点睛】本题考查了正方形的面积公式,开平方运算等,属于基础题.
10. 如图,作的任意一条直经,分别以为圆心,以的长为半径作弧,与相交于点和,顺次连接,得到六边形,则的面积与阴影区域的面积的比值为______;
【答案】
【解析】可将图中阴影部分的面积转化为两个等边三角形的面积之和,设⊙O的半径与等边三角形的边长为,分别表示出圆的面积和两个等边三角形的面积,即可求解
【详解】连接,,,,
由题可得:
为边长相等的等边三角形
可将图中阴影部分的面积转化为和的面积之和,如图所示:
设⊙O的半径与等边三角形的边长为,
⊙O的面积为
等边与等边的边长为
⊙O的面积与阴影部分的面积比为.
【点睛】本题考查了图形的面积转换,等边三角形面积以及圆面积的求法,将不规则图形的面积转换成规则图形的面积是解题关键.
11.如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
【答案】.
【解析】根据三角形内角和定理求出∠ACB,根据三角形的外角的性质求出∠BEF,根据扇形面积公式计算.
∵∠BAC=60°,∠ABC=100°,
∴∠ACB=20°,
又∵E为BC的中点,
∴BE=EC=BC=2,
∵BE=EF,
∴EF=EC=2,
∴∠EFC=∠ACB=20°,
∴∠BEF=40°,
∴扇形BEF的面积==
12.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________(结果保留).
【答案】24π cm
【解析】根据三视图确定该几何体是圆柱体,再计算圆柱体的侧面积.
【详解】解:先由三视图确定该几何体是圆柱体,底面半径是4÷2=2cm,高是6cm,
圆柱的侧面展开图是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,
且底面周长为:2π×2=4π(cm),
∴这个圆柱的侧面积是4π×6=24π(cm ).
故答案为:24π cm .
【点睛】主要考查由三视图确定几何体和求圆柱体的侧面积,关键是根据三视图确定该几何体是圆柱体.
13.如图,在半径为6的中,圆心角,则阴影部分面积为________.
【答案】
【解析】直接根据扇形的面积计算公式计算即可.
阴影部分面积为,
故答案为:.
【点睛】本题考查了扇形面积的计算,解题的关键是熟记扇形面积的计算公式.
14.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm2,则这个扇形的圆心角的度数是 度.
【答案】150
【解析】根据扇形面积公式求出圆锥的母线长,再根据弧长公式计算,得到答案.
设圆锥的母线长为lcm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20πcm,
∴圆锥的侧面展开图扇形的弧长为20πcm,
由题意得:×20π×l=240π,
解得:l=24,
则=20π,
解得,n=150,即扇形的圆心角为150°.
15.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB1C1D1的位置,则阴影部分的面积是 .
【答案】2﹣.
【解析】连接AE,根据旋转的性质推出Rt△AB1E≌Rt△ADE,再由含30度角的直角三角形性质得出DE=,最后由图可以得出S阴影部分=2(S正方形ABCD﹣S四边形ADEB1),将相关数值代入求解即可.如图,
连接AE,根据题意可知AB1=AD=1,∠B1=∠D=90°,∠BAB1=30°,
在Rt△AB1E和Rt△ADE中,
,
∴Rt△AB1E≌Rt△ADE(HL),
∵∠B1AE=∠DAE=∠B1AD=30°,
∴=,解得DE=,
∴S四边形ADEB1=2S△ADE=2××AD×DE=,
∴S阴影部分=2(S正方形ABCD﹣S四边形ADEB1)=2×(1﹣)=2﹣.
16.如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是 (结果保留π).
【答案】6π.
【解析】设圆锥的底面半径为r,母线长为l,根据题意得:2πr=,解得:l=3r,然后根据高为4,利用勾股定理得r2+42=(3r)2,从而求得底面半径和母线长,利用侧面积公式求得答案即可.
【解答】解:设圆锥的底面半径为r,母线长为l,
根据题意得:2πr=,
解得:l=3r,
∵高为4,
∴r2+42=(3r)2,
解得:r=,
∴母线长为3,
∴圆锥的侧面积为πrl=π××3=6π.
17.如图,点A是反比例函数y(x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A. 2 B. 4 C. 6 D. 8
【答案】A
【解析】连接OA、OB、PC.由于AC⊥y轴,根据三角形的面积公式以及反比例函数比例系数k的几何意义得到S△APC=S△AOC=3,S△BPC=S△BOC=1,然后利用S△PAB=S△APC﹣S△APB进行计算.
如图,
连接OA、OB、PC.
∵AC⊥y轴,
∴S△APC=S△AOC=×|6|=3,S△BPC=S△BOC=×|2|=1,
∴S△PAB=S△APC﹣S△BPC=2.
故选:A.
【点睛】本题考查了反比例函数的比例系数k的几何意义:在反比例函数图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
18.如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧,再分别以E、F为圆心,1为半径作圆弧、,则图中阴影部分的面积为( )
A. π﹣1 B. π﹣2 C. π﹣3 D. 4﹣π
【答案】B
【解析】根据题意和图形,可知阴影部分的面积是以2为半径的四分之一个圆(扇形)的面积减去以1为半径的半圆(扇形)的面积再减去2个以边长为1的正方形的面积减去以1半径的四分之一个圆(扇形)的面积,本题得以解决.
由题意可得,
阴影部分的面积是: π×22﹣﹣2(1×1﹣ π×12)=π﹣2,
故选:B.
【点睛】主要考查运用正方形的性质,圆的面积公式(或扇形的面积公式),正方形的面积公式计算不规则几何图形的面积,解题的关键是理解题意,观察图形,合理分割,转化为规则图形的面积和差进行计算.
19.如图1,在平面直角坐标系中,在第一象限,且轴.直线从原点出发沿轴正方向平移.在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图2所示.那么的面积为( )
A. 3 B. C. 6 D.
【答案】B
【解析】根据图象可以得到当移动的距离是4时,直线经过点A;当移动距离是6时,直线经过B,在移动距离是7时经过D,则AD=7-4=3,当直线经过D点,设交BC与N.则DN=2,作DM⊥AB于点M.利用三角函数即可求得DM即平行四边形的高,然后利用平行四边形的面积公式即可求解.
【详解】根据图象可以得到当移动的距离是4时,直线经过点A
当移动距离是6时,直线经过B
当移动距离是7时经过D,则AD=7-4=3
如图:设交BC与N,则DN=2,作DM⊥AB于点M,
∵移动直线为y=x
∴∠NDM=45°
∴DM=cos∠NDM·ND=
∴的面积为AD×DM=3×=3.
故答案为B.
【点睛】本题考查了平移变换、解直角三角形等知识,其中根据平移变换确定AD的长是解答本题的关键.
20.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 .
【答案】8.
【解析】由三角形的中位线定理证得DE∥AB,AB=2DE=4,进而证得四边形ABFD是平行四边形,在Rt△ABC中,根据勾股定理求出BC=4,得到BE=2,根据平行四边形的面积公式即可求出四边形ABFD的面积.
∵D、E分别为AC、BC的中点,
∵DE是△ABC的中位线,
∴DE∥AB,DE=AB,
∴AB=2DE,DF∥AB,
又∵BF∥AC,
∴BF∥AD,
∴四边形ABFD是平行四边形,
∵AB⊥BE,
∴S平行四边形ABFD=AB BE,
∵DE=2,
∴AB=2×2=4,
在Rt△ABC中,
∵∠C=30°,
∴AC=2AB=2×4=8,
∴BC===4,
∴BE=BC=2,
∴S平行四边形ABFD=4×2=8,故答案为8.
21.如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E、F、G、N、M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
【答案】1:3.
【解析】通过证明△AEM∽△ABC,可得,可求EF的长,由相似三角形的性质可得=()2=,即可求解.
∵四边形EFGH和四边形HGNM均为正方形,
∴EF=EH=HM,EM∥BC,
∴△AEM∽△ABC,
∴,
∴,
∴EF=,
∴EM=5,
∵△AEM∽△ABC,
∴=()2=,
∴S四边形BCME=S△ABC﹣S△AEM=3S△AEM,
∴△AEM与四边形BCME的面积比为1:3,故答案为:1:3.
22.如图,△ABC中,∠ABC=90°,AB=2,AC=4,点O为BC的中点,以O为圆心,以OB为半径作半圆,交AC于点D,则图中阴影部分的面积是 .
【答案】﹣.
【解析】根据题意,作出合适的辅助线,即可求得DE的长、∠
DOB的度数,然后根据图形可知阴影部分的面积是△ABC的面积减去△COD的面积和扇形BOD的面积,从而可以解答本题.
连接OD,过D作DE⊥BC于E,
在△ABC中,∠ABC=90°,AB=2,AC=4,
∴sinC===,BC===2,
∴∠C=30°,
∴∠DOB=60°,
∵OD=BC=,
∴DE=,
∴阴影部分的面积是:2×2﹣﹣=﹣,
故答案为:﹣.
23.若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
【答案】4.
【解析】连接CD.构建直径所对的圆周角∠BDC=90°,然后利用等腰直角△ABC的性质:斜边上的中线是斜边的一半、中线与垂线重合,求得CD=BD=AD,从而求得弦BD与CD所对的弓形的面积相等,所以图中阴影部分的面积=直角三角形ABC的面积﹣直角三角形BCD的面积.
解:连接CD.
∵BC是直径,
∴∠BDC=90°,即CD⊥AB;
又∵△ABC为等腰直角三角形,
∴CD是斜边AB的垂直平分线,
∴CD=BD=AD,
∴=,
∴S弓形BD=S弓形CD,
∴S阴影=SRt△ABC﹣SRt△BCD;
∵△ABC为等腰直角三角形,CD是斜边AB的垂直平分线,
∴SRt△ABC=2SRt△BCD;
又SRt△ABC=×4×4=8,
∴S阴影=4.
24.如图,从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为 dm2.
【答案】2π.
【解析】连接AC,根据圆周角定理得出AC为圆的直径,解直角三角形求出AB,根据扇形面积公式求出即可.
连接AC,
∵从一块直径为4dm的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,
∴AC为直径,即AC=4dm,AB=BC(扇形的半径相等),
∵AB2+BC2=22,
∴AB=BC=2dm,
∴阴影部分的面积是=2π(dm2).
25.如图,A、B两点在反比例函数y=﹣(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是 .
【答案】6
【解析】过A作AH⊥OC,过B作BG⊥OC,根据已知条件结合反比例函数k的几何意义,求出点A与点B的坐标关系,再确定△ACH与△AOH的面积.
解:过A作AH⊥OC,过B作BG⊥OC,
∵A、B两点在反比例函数y=﹣(x<0)的图象上,
∴设A(x,﹣),S△AOH=,
∵AB=2BC,
∴,,
∴BG=AH,HG=2CG
∴点B的纵坐标为,代反比例函数中得点B的坐标为(3x,),
∴OG=﹣3x,HG=﹣2x,CG=﹣x,则OC=﹣4x,
∴S△AOC== (﹣4x) (﹣)=6
26.如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是 .(结果保留π)
【答案】π﹣.
【解析】由∠C=45°根据圆周角定理得出∠AOB=90°,根据S阴影=S扇形AOB﹣S△AOB可得出结论.
∵∠C=45°,
∴∠AOB=90°,
∴S阴影=S扇形AOB﹣S△AOB
=
=π﹣.
27.如图所示的扇形中,,C为上一点,,连接,过C作的垂线交于点D,则图中阴影部分的面积为_______.
【答案】
【解析】先根据题目条件计算出OD,CD的长度,判断为等边三角形,之后表示出阴影面积的计算公式进行计算即可.
在中,
∴
∵
∴
∵
∴为等边三角形
∴
故答案为:
【点睛】本题考查了阴影面积的计算,熟知不规则阴影面积的计算方法是解题的关键.
28.如图,在中,,点D为AB的中点,以点D为圆心作圆心角为90°的扇形,点C恰好在上,则图中阴影部分的面积为________.
【答案】
【解析】如解图,连接,过点作于点,于点.
设交于点,交于点,
,,点为的中点,,,
,四边形是正方形,,
则,
,
,
在和中,,
,
,
.
29.如图,已知半圆的直径,点在半圆上,以点为圆心,为半径画弧交于点,连接.若,则图中阴影部分的面积为______.(结果不取近似值)
【答案】
【解析】根据60°特殊角求出AC和BC,再算出△ABC的面积,根据扇形面积公式求出扇形的面积,再用三角形的面积减去扇形面积即可.
【详解】∵AB是直径,
∴∠ACB=90°,∠ABC=60°,
∴BC=,AC=,
∴,
由以上可知∠CAB=30°,
∴扇形ACD的面积=,
∴阴影部分的面积为.
30.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2、BB2,求△ABB2的面积.
【答案】见解析。
【解析】(1)根据网格结构找出点A1、B1的位置,然后顺次连接即可;
(2)根据网格结构找出点B2的位置,然后连接即可;
(3)利用正方形的面积减去三个三角形的面积,列式计算即可得解.
解:(1)线段A1B1如图所示;
(2)线段A1B2如图所示;
(3)S=4×4﹣×2×2﹣×2×4﹣×2×4=6.
【点拨】本题考查了平移变换和旋转变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
31.如图,半圆的直径AB=6,点C在半圆上,∠BAC=30°,则阴影部分的面积为 (结果保留π).
【答案】3π﹣.
【解析】根据题意,作出合适的辅助线,即可求得CD和∠COB的度数,即可得到阴影部分的面积是半圆的面积减去△AOC和扇形BOC的面积.
连接OC、BC,作CD⊥AB于点D,
∵直径AB=6,点C在半圆上,∠BAC=30°,
∴∠ACB=90°,∠COB=60°,
∴AC=3,
∵∠CDA=90°,
∴CD=,
∴阴影部分的面积是:=3π﹣
【点评】本题考查扇形面积的计算、圆周角定理,解答本题的关键是明确题意,利用数形结合的思想解答.
32.如图,菱形ABCD的边长为4cm,∠A=60°,BD是以点A为圆心,AB长为半径的弧,CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为 cm2.
【答案】4.
【解析】连接BD,判断出△ABD是等边三角形,根据等边三角形的性质可得∠ABD=60°,再求出∠CBD=60°,然后求出阴影部分的面积=S△ABD,计算即可得解.
如图,连接BD,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠ABD=60°,
又∵菱形的对边AD∥BC,
∴∠ABC=180°﹣60°=120°,
∴∠CBD=120°﹣60°=60°,
∴S阴影=S扇形BDC﹣(S扇形ABD﹣S△ABD),
=S△ABD,
=×4×=4cm2.
故答案为:4.
33.某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
【答案】见解析。
【解析】(1)设∠BAC=n°.根据弧EF的两种求法,构建方程,可得结论.
(2)根据S阴= BC AD﹣S扇形AEF求解即可.
解:(1)设∠BAC=n°.
由题意得π DE=,AD=2DE,
∴n=90,∴∠BAC=90°.
(2)∵AD=2DE=10(cm),
∴S阴= BC AD﹣S扇形AEF=×10×20﹣=(100﹣25π)cm2.
34. 【阅读理解】如图,,的面积与的面积相等吗?为什么?
解:相等在和中,分别作,,垂足分别为E,F.
,
.
,
四边形AEFD是平行四边形,
.
又,.
.
【类比探究】如图,在正方形ABCD的右侧作等腰,,,连接AE,求的面积.
解:过点E作于点F,连接AF.
请将余下的求解步骤补充完整.
【拓展应用】如图,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,,连接BD,BF,DF,直接写出的面积.
【答案】见解析。
【解析】【类比探究】由等腰三角形的性质可得,,可证,可得,由三角形的面积公式可求解;
【拓展应用】连接CF,由正方形的性质可得,可得,可得,由三角形的面积公式可求解.
本题是四边形综合题,考查了正方形的性质,等腰三角形的性质,三角形面积公式等知识,能掌握和运用“阅读理解”中的知识是解题的关键.
【类比探究】过点E作于点F,连接AF,
四边形ABCD是正方形,
,,
,,
,,
,
,
;
【拓展应用】如图,连接CF,
四边形ABCD和四边形CGFE都是正方形,
,,
,
,
,
.
35. 如图,在中,于点D,,,,点E是AD上一动点不与点A,D重合,在内作矩形EFGH,点F在DC上,点G,H在AC上,设,连接BE.
(1)当矩形EFGH是正方形时,直接写出EF的长;
(2)设的面积为,矩形EFGH的面积为,令,求y关于x的函数解析式不要求写出自变量x的取值范围;
(3)如图,点是中得到的函数图象上的任意一点,过点P的直线l分别与x轴正半轴,y轴正半轴交于M,N两点,求面积的最小值,并说明理由.
【答案】见解析。
【解析】设.
,,
,
,
,
,
,
,
四边形EFGH是正方形,
,,
,
,
,,
,,
,
,
.
,,
,
,,
,
.
如图中,由可知点P在上,
当OP最小时,点P在第一象限的角平分线时,此时,
当直线时,的面积最小,
此时,
的面积的最小值.
同课章节目录
