2025中考数学复习冲刺之特色微专题巩固_专题12 新定义型数学中考问题(含解析)
文档属性
| 名称 | 2025中考数学复习冲刺之特色微专题巩固_专题12 新定义型数学中考问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 936.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览



文档简介
专题12 新定义型数学中考问题
1. 我们发现:,,,…,,一般地,对于正整数,,如果满足时,称为一组完美方根数对.如上面是一组完美方根数对.则下面4个结论:①是完美方根数对;②是完美方根数对;③若是完美方根数对,则;④若是完美方根数对,则点在抛物线上.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.在实数范围内定义运算“☆”:,例如:.如果,则的值是( ).
A. B. 1 C. 0 D. 2
3.定义新运算“ ”,规定:a b=a﹣2b.若关于x的不等式x m>3的解集为x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
4.对于任意的有理数a,b,如果满足+=,那么我们称这一对数a,b为“相随数对”,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]=( )
A.﹣2 B.﹣1 C.2 D.3
5.定义一种运算:,则不等式的解集是( )
A. 或 B.
C. 或 D. 或
6.定义a b=2a+,则方程3 x=4 2的解为( )
A.x= B.x= C.x= D.x=
7.定义:一次函数y=ax+b的特征数为[a,b],若一次函数y=﹣2x+m的图象向上平移3个单位长度后与反比例函数y=﹣的图象交于A,B两点,且点A,B关于原点对称,则一次函数y=﹣2x+m的特征数是( )
A.[2,3] B.[2,﹣3] C.[﹣2,3] D.[﹣2,﹣3]
8. 规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
9.定义:[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[m,1﹣m,2﹣m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当x>时,y随x的增大而减小.其中所有正确结论的序号是 .
10.我们规定:若=(x1,y1),=(x2,y2),则 =x1x2+y1y2.例如=(1,3),=(2,4),则 =1×2+3×4=2+12=14.已知=(x+1,x﹣1),=(x﹣3,4),且﹣2≤x≤3,则 的最大值是 .
11.规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
12.若把第n个位置上的数记为xn,则称x1,x2,x3,…,xn有限个有序放置的数为一个数列A.定义数列A的“伴生数列”B是:y1,y2,y3,…,yn,其中yn是这个数列中第n个位置上的数,n=1,2,…,k且yn=并规定x0=xn,xn+1=x1.如果数列A只有四个数,且x1,x2,x3,x4依次为3,1,2,1,则其“伴生数列”B是 .
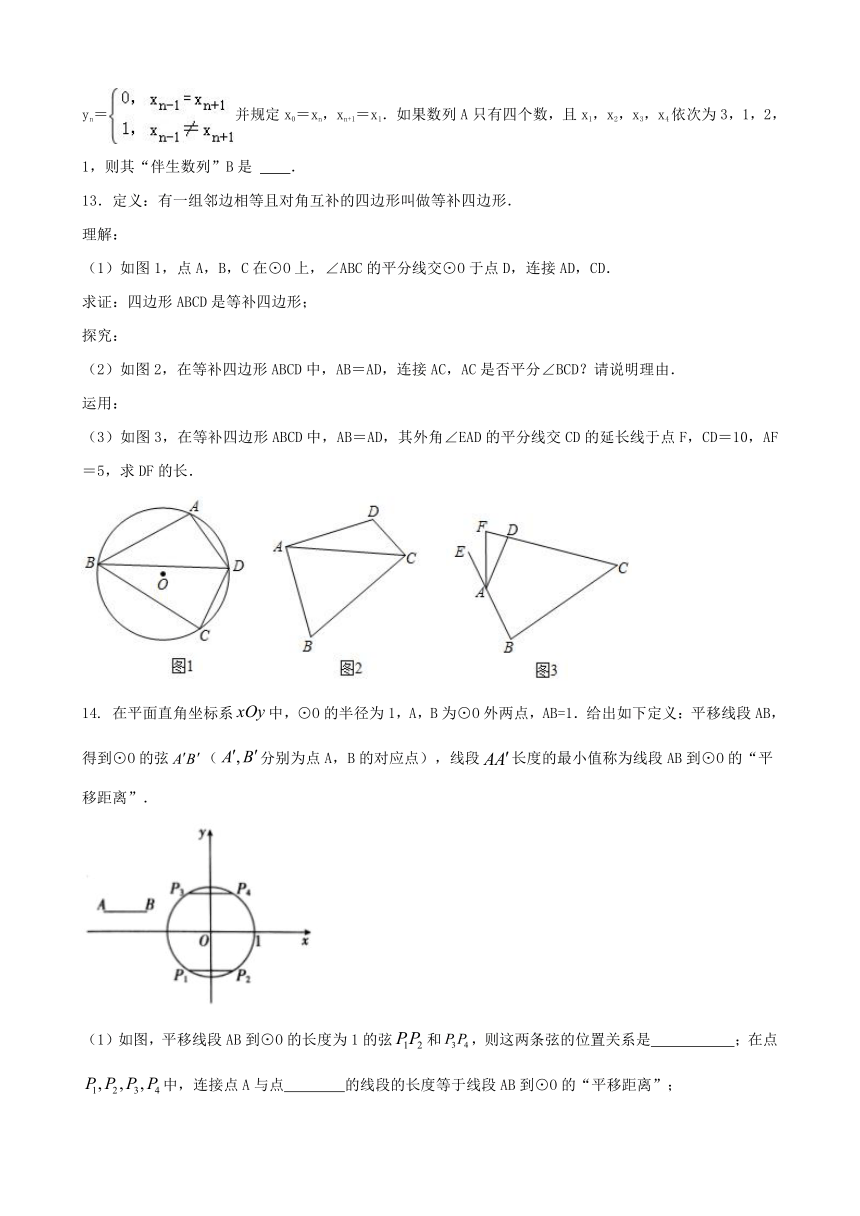
13.定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.
求证:四边形ABCD是等补四边形;
探究:
(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.
运用:
(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,求DF的长.
14. 在平面直角坐标系中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦(分别为点A,B的对应点),线段长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB到⊙O的长度为1的弦和,则这两条弦的位置关系是 ;在点中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线上,记线段AB到⊙O的“平移距离”为,求的最小值;
(3)若点A的坐标为,记线段AB到⊙O的“平移距离”为,直接写出的取值范围.
15.定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,∥,,过点D作BD垂线交BC的延长线于点E,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形内接于⊙O中,.求⊙O的半径.
16.在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如(1,1),(2021,2021)…都是“雁点”.
(1)求函数y=图象上的“雁点”坐标;
(2)若抛物线y=ax2+5x+c上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当a>1时.
①求c的取值范围;
②求∠EMN的度数;
(3)如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左侧),P是抛物线y=﹣x2+2x+3上一点,连接BP,以点P为直角顶点,构造等腰Rt△BPC,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.
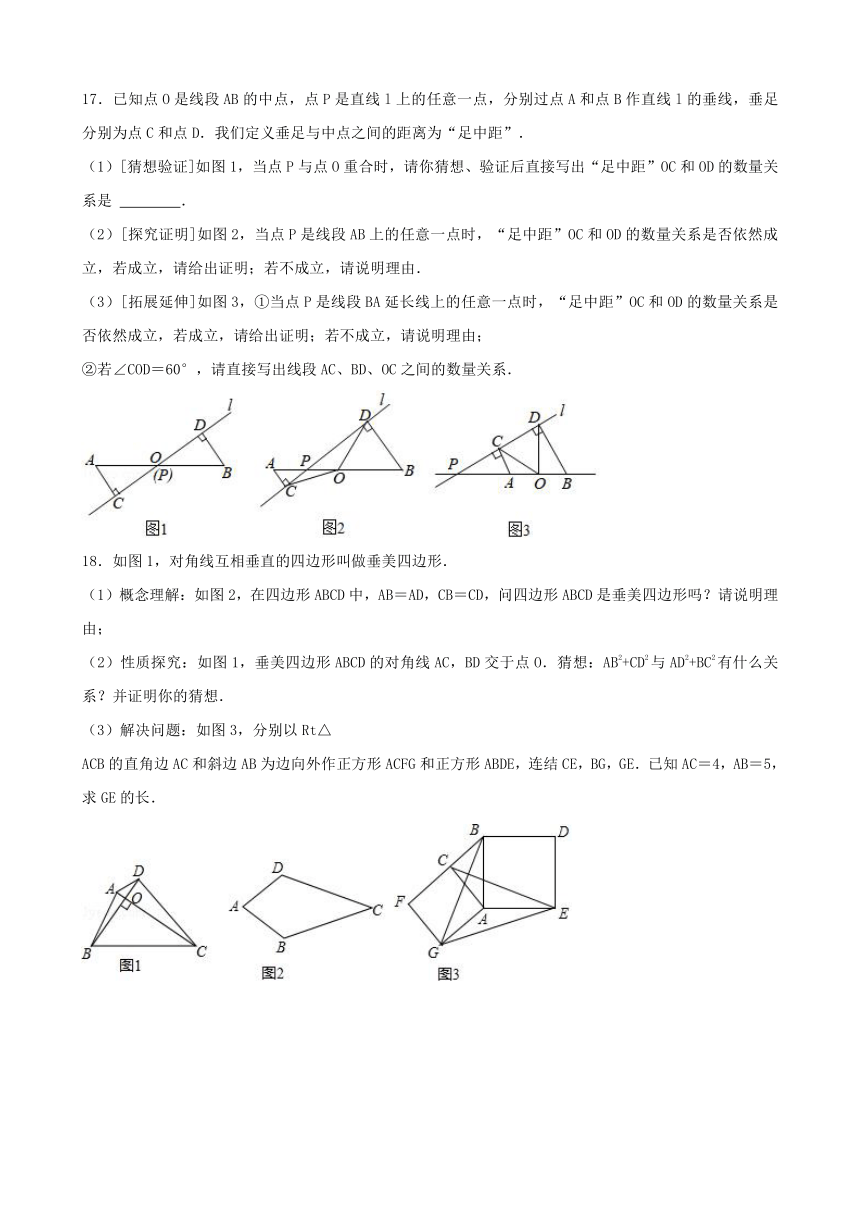
17.已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中距”.
(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 .
(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.
18.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,垂美四边形ABCD的对角线AC,BD交于点O.猜想:AB2+CD2与AD2+BC2有什么关系?并证明你的猜想.
(3)解决问题:如图3,分别以Rt△
ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE,BG,GE.已知AC=4,AB=5,求GE的长.
专题12 新定义型数学中考问题(解析版)
1. 我们发现:,,,…,,一般地,对于正整数,,如果满足时,称为一组完美方根数对.如上面是一组完美方根数对.则下面4个结论:①是完美方根数对;②是完美方根数对;③若是完美方根数对,则;④若是完美方根数对,则点在抛物线上.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】根据定义逐项分析判断即可.
,
是完美方根数对;
故①正确;
不是完美方根数对;
故②不正确;
若是完美方根数对,则
即
解得或
是正整数
则
故③正确;
若是完美方根数对,则
,
即
故④正确
故选C
【点睛】本题考查了求算术平方根,解一元二次方程,二次函数的定义,理解定义是解题的关键.
2.在实数范围内定义运算“☆”:,例如:.如果,则的值是( ).
A. B. 1 C. 0 D. 2
【答案】C
【解析】本题考查了实数的计算,一元一次方程的解法,本题的关键是能看明白题目意思,根据新定义的运算规则求解即可
根据题目中给出的新定义运算规则进行运算即可求解.
由题意知:,
又,
∴,
∴.
3.定义新运算“ ”,规定:a b=a﹣2b.若关于x的不等式x m>3的解集为x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
【答案】B
【解析】根据定义新运算的法则得出不等式,解不等式;根据解集列方程即可.
∵a b=a﹣2b,
∴x m═x﹣2m.
∵x m>3,
∴x﹣2m>3,
∴x>2m+3.
∵关于x的不等式x m>3的解集为x>﹣1,
∴2m+3=﹣1,
∴m=﹣2.
4.对于任意的有理数a,b,如果满足+=,那么我们称这一对数a,b为“相随数对”
,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]=( )
A.﹣2 B.﹣1 C.2 D.3
【答案】A
【解析】根据(m,n)是“相随数对”得出9m+4n=0,再将原式化成9m+4n﹣2,最后整体代入求值即可.
∵(m,n)是“相随数对”,
∴+=,
∴=,
即9m+4n=0,
∴3m+2[3m+(2n﹣1)]
=3m+2[3m+2n﹣1]
=3m+6m+4n﹣2
=9m+4n﹣2
=0﹣2
=﹣2,
5.定义一种运算:,则不等式的解集是( )
A. 或 B.
C. 或 D. 或
【答案】C
【解析】由新定义得或,
解得或
6.定义a b=2a+,则方程3 x=4 2的解为( )
A.x= B.x= C.x= D.x=
【答案】B
【解析】利用题中的新定义化简已知等式,求出解即可得到x的值.
根据题中的新定义得:
3 x=2×3+,
4 2=2×4+,
∵3 x=4 2,
∴2×3+=2×4+,
解得:x=,
经检验,x=是分式方程的根.
7.定义:一次函数y=ax+b的特征数为[a,b],若一次函数y=﹣2x+m的图象向上平移3个单位长度后与反比例函数y=﹣的图象交于A,B两点,且点A,B关于原点对称,则一次函数y=﹣2x+m的特征数是( )
A.[2,3] B.[2,﹣3] C.[﹣2,3] D.[﹣2,﹣3]
【答案】D
【解析】将一次函数y=﹣2x+m的图像向上平移3个单位长度后,得到解析式y=﹣2x+m+3,联立一次函数与反比例函数解析式,得到关于x的一元二次方程,设A(x1,0),B(x2,0),所以x1与x2是一元二次方程的两根,根据根与系数关系,得到,又A,B两点关于原点对称,所以x1+x2=0,则,得到m=﹣3,根据定义,得到一次函数y=﹣2x+m的特征数是[﹣2,﹣3].
解:将一次函数y=﹣2x+m向上平移3个单位长度后得到y=﹣2x+m+3,
设A(x1,0),B(x2,0),
联立,
∴2x2﹣(m+3)x﹣3=0,
∵x1和x2是方程的两根,
∴,
又∵A,B两点关于原点对称,
∴x1+x2=0,
∴,
∴m=﹣3,
根据定义,一次函数y=﹣2x+m的特征数是[﹣2,﹣3],
故选:D.
8. 规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
【答案】或
【解析】分两种情况,根据关于y轴对称的图形的对称点的坐标特点,即可求得.
函数(k为常数)的“Y函数”图象与x轴只有一个交点,
函数(k为常数)的图象与x轴也只有一个交点,
当k=0时,函数解析为,它的“Y函数”解析式为,它们的图象与x轴只有一个交点,
当时,此函数是二次函数,
它们的图象与x轴都只有一个交点,
它们的顶点分别在x轴上,
,得,
故k+1=0,解得k=-1,
故原函数的解析式为,
故它的“Y函数”解析式为,
故答案为:或.
【点睛】本题考查了新定义,二次函数图象与x轴的交点问题,坐标与图形变换-轴对称,求一次函数及二次函数的解析式,理解题意和采用分类讨论的思想是解决本题的关键.
9.定义:[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[m,1﹣m,2﹣m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当x>时,y随x的增大而减小.其中所有正确结论的序号是 .
【答案】①②③.
【解析】根据特征数的定义,写出二次函数的表达式为y=mx2+(1﹣m)x+2﹣m.①写出对称轴方程后把m=1代入即可判断;②把m=2代入即可判断;③根据开口方向即可判断;④根据对称轴,开口方向,增减性即可判断.
由特征数的定义可得:特征数为[m,1﹣m,2﹣m]的二次函数的表达式为y=mx2+(1﹣m)x+2﹣m.
∵此抛物线的的对称轴为直线x===,
∴当m=1时,对称轴为直线x=0,即y轴.故①正确;
∵当m=2时,此二次函数表达式为y=2x2﹣x,令x=0,则y=0,
∴函数图象过原点,故②正确;
∵当m>0时,二次函数图象开口向上,函数有最小值,故③正确;
∵m<0,
∴对称轴x==,抛物线开口向下,
∴在对称轴的右侧,y随x的增大而减小.
即x>时,y随x的增大而减小.
故④错误.故答案为:①②③.
10.我们规定:若=(x1,y1),=(x2,y2),则 =x1x2+y1y2.例如=(1,3),=(2,4),则 =1×2+3×4=2+12=14.已知=(x+1,x﹣1),=(x﹣3,4),且﹣2≤x≤3,则 的最大值是 .
【答案】8.
【解析】根据平面向量的新定义运算法则,列出关于x的二次函数,根据二次函数最值的求法解答即可.
根据题意知: =(x+1)(x﹣3)+4(x﹣1)=(x+1)2﹣8.
因为﹣2≤x≤3,
所以当x=3时, =(3+1)2﹣8=8.
即 的最大值是8.
11.规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°
后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
【答案】(1)B;(2)(1)(3)(5);(3)C;(4)见解析
【解析】(1)根据旋转对称图形的定义进行判断;
(2)先分别求每一个图形中的旋转角,然后再进行判断;
(3)根据旋转对称图形的定义进行判断;
(4)利用旋转对称图形的定义进行设计.
解:(1)矩形、正五边形、菱形、正六边形都是旋转对称图形,但正五边形不是中心对称图形,
故选:B.
(2)是旋转对称图形,且有一个旋转角是60度的有(1)(3)(5).
故答案为:(1)(3)(5).
(3)①中心对称图形,旋转180°一定会和本身重合,是旋转对称图形;故命题①正确;
②等腰三角形绕一个定点旋转一定的角度α(0°<α≤180°)后,不一定能与自身重合,只有等边三角形是旋转对称图形,故②不正确;
③圆具有旋转不变性,绕圆心旋转任意角度一定能与自身重合,是旋转对称图形;故命题③正确;
即命题中①③正确,
故选:C.
(4)图形如图所示:
【点拨】考查旋转对称图形,中心对称图形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
12.若把第n个位置上的数记为xn,则称x1,x2,x3,…,xn有限个有序放置的数为一个数列A.定义数列A的“伴生数列”B是:y1,y2,y3,…,yn,其中yn是这个数列中第n个位置上的数,n=1,2,…,k且yn=并规定x0=xn,xn+1=x1.如果数列A只有四个数,且x1,x2,x3,x4依次为3,1,2,1,则其“伴生数列”B是 .
【答案】0,1,0,1.
【解析】根据“伴生数列”的定义依次取n=1,2,3,4,求出对应的yn即可.
当n=1时,x0=x4=1=x2,
∴y1=0,
当n=2时,x1≠x3,
∴y2=1,
当n=3时,x2=x4,
∴y3=0,
当n=4时,x3≠x5=x1,
∴y4=1,
∴“伴生数列”B是:0,1,0,1,
故答案为0,1,0,1.
13.定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.
求证:四边形ABCD是等补四边形;
探究:
(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.
运用:
(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,求DF的长.
【答案】见解析。
【解析】(1)由圆内接四边形互补可知∠A+∠C=180°,∠ABC+∠ADC=180°,再证AD=CD,即可根据等补四边形的定义得出结论;
(2)过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,证△ABE≌△ADF,得到AE=AF,根据角平分线的判定可得出结论;
(3)连接AC,先证∠EAD=∠BCD,推出∠FCA=∠FAD,再证△ACF∽△DAF,利用相似三角形对应边的比相等可求出DF的长.
【解答】(1)证明:∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,∠ABC+∠ADC=180°,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴,
∴AD=CD,
∴四边形ABCD是等补四边形;
(2)AD平分∠BCD,理由如下:
如图2,过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,
则∠AEB=∠AFD=90°,
∵四边形ABCD是等补四边形,
∴∠B+∠ADC=180°,
又∠ADC+∠ADF=180°,
∴∠B=∠ADF,
∵AB=AD,
∴△ABE≌△ADF(AAS),
∴AE=AF,
∴AC是∠BCF的平分线,即AC平分∠BCD;
(3)如图3,连接AC,
∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180°,
又∠BAD+∠EAD=180°,
∴∠EAD=∠BCD,
∵AF平分∠EAD,
∴∠FAD=∠EAD,
由(2)知,AC平分∠BCD,
∴∠FCA=∠BCD,
∴∠FCA=∠FAD,
又∠AFC=∠DFA,
∴△ACF∽△DAF,
∴,
即,
∴DF=5﹣5.
【点评】考查新定义等补四边形,圆的有关性质,全等三角形的判定与性质,角平分线的判定,相似三角形的判定与性质等,解题关键是要能够通过自主学习来进行探究,运用等.
14. 在平面直角坐标系中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦(分别为点A,B的对应点),线段长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB到⊙O的长度为1的弦和,则这两条弦的位置关系是 ;在点中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线上,记线段AB到⊙O的“平移距离”为,求的最小值;
(3)若点A的坐标为,记线段AB到⊙O的“平移距离”为,直接写出的取值范围.
【答案】(1)平行,P3;(2);(3)
【解析】(1)根据圆的性质及“平移距离”的定义填空即可;
(2)过点O作OE⊥AB于点E,交弦CD于点F,分别求出OE、OF的长,由得到的最小值;
(3)线段AB的位置变换,可以看作是以点A为圆心,半径为1的圆,只需在⊙O内找到与之平行,且长度为1的弦即可.平移距离的最大值即点A,B点的位置,由此得出的取值范围.
【详解】解:(1)平行;P3;
(2)如图,线段AB在直线上,平移之后与圆相交,得到的弦为CD,CD∥AB,过点O作OE⊥AB于点E,交弦CD于点F,OF⊥CD,令,直线与x轴交点为(-2,0),直线与x轴夹角为60°,∴.
由垂径定理得:,
∴;
(3)线段AB的位置变换,可以看作是以点A为圆心,半径为1的圆,只需在⊙O内找到与之平行,且长度为1的弦即可;
点A到O的距离为.
如图,平移距离的最小值即点A到⊙O的最小值:;
平移距离的最大值线段是下图AB的情况,即当A1,A2关于OA对称,且A1B2⊥A1A2且A1B2=1时.∠B2A2A1=60°,则∠OA2A1=30°,
∵OA2=1,∴OM=, A2M=,
∴MA=3,AA2= ,
∴的取值范围为:.
【点睛】本题考查圆的基本性质及与一次函数的综合运用,熟练掌握圆的基本性质、点与圆的位置关系、直线与圆的位置关系是解题的关键.
15.定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,∥,,过点D作BD垂线交BC的延长线于点E,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形内接于⊙O中,.求⊙O的半径.
【答案】(1)④;(2)证明过程见解析;③4
【解析】(1)根据垂等四边形的性质对每个图形判断即可;
(2)根据已知条件可证明四边形ACED是平行四边形,即可得到AC=DE,再根据等腰直角三角形的性质即可得到结果;
(3)过点O作,根据面积公式可求得BD的长,根据垂径定理即可得到答案.
【详解】(1)①平行四边形的对角线互相平分但不垂直和相等,故不是;②矩形对角线相等但不垂直;③菱形的对角线互相垂直但不相等;④正方形的对角线互相垂直且相等,故正方形是垂等四边形;
(2)∵,,
∴AC∥DE,
又∵∥,
∴四边形ADEC是平行四边形,
∴AC=DE,
又∵,
∴△BDE是等腰直角三角形,
∴BD=DE,
∴BD=AC,
∴四边形是垂等四边形.
(3)如图,过点O作,
∵四边形是垂等四边形,
∴AC=BD,
又∵垂等四边形的面积是24,,根据垂等四边形的面积计算方法得:
,
又∵,
∴,
设半径为r,根据垂径定理可得:
在△ODE中,OD=r,DE=,
∴,
∴的半径为4.
【点睛】本题主要考查了四边形性质与圆的垂径定理应用,准确理解新定义的垂等四边形的性质是解题的关键.
16.在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如(1,1),(2021,2021)…都是“雁点”.
(1)求函数y=图象上的“雁点”坐标;
(2)若抛物线y=ax2+5x+c上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当a>1时.
①求c的取值范围;
②求∠EMN的度数;
(3)如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左侧),P是抛物线y=﹣x2+2x+3上一点,连接BP,以点P为直角顶点,构造等腰Rt△BPC,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】见解析。
【解析】(1)由题意得:x=,解得x=±2,即可求解;
(2)①由△=25﹣4ac=0,即ac=4,即可求解;
②求出点M的坐标为(﹣,0)、点E的坐标为(﹣,﹣),即可求解;
(3)证明△CMP≌△PNB(AAS),则PM=BN,CM=PN,即可求解.
解:(1)由题意得:x=,解得x=±2,
当x=±2时,y==±2,
故“雁点”坐标为(2,2)或(﹣2,﹣2);
(2)①∵“雁点”的横坐标与纵坐标相等,
故“雁点”的函数表达式为y=x,
∵物线y=ax2+5x+c上有且只有一个“雁点”E,
则ax2+5x+c=x,
则△=25﹣4ac=0,即ac=4,
∵a>1,
故c<4;
②∵ac=4,则ax2+5x+c=0为ax2+5x+=0,
解得x=﹣或﹣,即点M的坐标为(﹣,0),
由ax2+5x+c=x,ac=4,
解得x=﹣,即点E的坐标为(﹣,﹣),
故点E作EH⊥x轴于点H,
则HE=,MH=xE﹣xM=﹣﹣(﹣)==HE,
故∠EMN的度数为45°;
(3)存在,理由:
由题意知,点C在直线y=x上,故设点C的坐标为(t,t),
过点P作x轴的平行线交过点C与y轴的平行线于点M,交过点B与y轴的平行线于点N,
设点P的坐标为(m,﹣m2+2m+3),
则BN=﹣m2+2m+3,PN=3﹣m,PM=m﹣t,CM=﹣m2+2m+3﹣t,
∵∠NPB+∠MPC=90°,∠MPC+∠CPM=90°,
∴∠NPB=∠CPM,
∵∠CMP=∠PNB=90°,PC=PB,
∴△CMP≌△PNB(AAS),
∴PM=BN,CM=PN,
即m﹣t=|﹣m2+2m+3|,﹣m2+2m+3﹣t=|3﹣m|,
解得m=1+(舍去)或1﹣或,
故点P的坐标为(,)或(,).
17.已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中距”.
(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 .
(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.
【答案】见解析。
【分析】(1)猜想:OC=OD.证明Rt△AOC≌Rt△BOD(HL),可得结论.
(2)结论成立.过点O作直线EF∥CD,交BD于点F,延长AC交EF于点E,证明△COE≌DOF(SAS),可得结论.
(3)①结论成立.如图3中,延长CO交BD于点E,证明CO=OE,再利用直角三角形斜边中线的性质解决问题即可.
②结论:AC+BD=OC.利用等边三角形的判定和性质以及全等三角形的性质证明即可.
解:(1)猜想:OC=OD.
理由:如图1中,∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°
在Rt△AOC与Rt△BOD中,
,
∴Rt△AOC≌Rt△BOD(HL),
∴OC=OD,
故答案为:OC=OD;
(2)数量关系依然成立.
理由:过点O作直线EF∥CD,交BD于点F,延长AC交EF于点E,
∵EF∥CD,
∴∠DCE=∠E=∠CDF=90°,
∴四边形CEFD为矩形,
∴∠OFD=90°,CE=DF,
由(1)知,OE=OF,
在△COE与△DOF中,
,
∴△COE≌DOF(SAS),
∴OC=OD;
(3)①结论成立.
理由:如图3中,延长CO交BD于点E,
∵AC⊥CD,BD⊥CD,
∴AC∥BD,
∴∠A=∠B,
∵点O为AB的中点,
∴AO=BO,
又∵∠AOC=∠BOE,
∴△AOC≌△BOE(AAS),
∴CO=CE,
∵∠CDE=90°,
∴OD=OC=OE,
∴OC=OD.
②结论:AC+BD=OC.
理由:如图3中,∵∠COD=60°,OD=OC,
∴△COD是等边三角形,
∴CD=OC,∠OCD=60°,
∵∠CDE=90°,
∴tan60°=,
∴DE=CD,
∴△AOC≌△BOE,
∴AC=BE,
∴AC+BD=BD+BE=DE=CD,
∴AC+BD=OC.
18.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,垂美四边形ABCD的对角线AC,BD交于点O.猜想:AB2+CD2与AD2+BC2有什么关系?并证明你的猜想.
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE,BG,GE.已知AC=4,AB=5,求GE的长.
【答案】见解析.
【解析】(1)连接AC、BD,根据垂直平分线的判定定理证明即可;
(2)根据垂直的定义和勾股定理解答即可;
(3)如图3,连接CG、BE,根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
解:(1)四边形ABCD是垂美四边形.
理由如下:如图2,连接AC、BD,
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)AB2+CD2=AD2+BC2,
理由如下:
如图1中,
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2;
(3)如图3,连接CG、BE,
∵正方形ACFG和正方形ABDE,
∴AG=AC,AB=AE,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
∵∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC===3,
∵CG===4,BE===5,
∴GE2=CG2+BE2﹣CB2=(4)2+(5)2﹣32=73,
∴GE=.
1. 我们发现:,,,…,,一般地,对于正整数,,如果满足时,称为一组完美方根数对.如上面是一组完美方根数对.则下面4个结论:①是完美方根数对;②是完美方根数对;③若是完美方根数对,则;④若是完美方根数对,则点在抛物线上.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.在实数范围内定义运算“☆”:,例如:.如果,则的值是( ).
A. B. 1 C. 0 D. 2
3.定义新运算“ ”,规定:a b=a﹣2b.若关于x的不等式x m>3的解集为x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
4.对于任意的有理数a,b,如果满足+=,那么我们称这一对数a,b为“相随数对”,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]=( )
A.﹣2 B.﹣1 C.2 D.3
5.定义一种运算:,则不等式的解集是( )
A. 或 B.
C. 或 D. 或
6.定义a b=2a+,则方程3 x=4 2的解为( )
A.x= B.x= C.x= D.x=
7.定义:一次函数y=ax+b的特征数为[a,b],若一次函数y=﹣2x+m的图象向上平移3个单位长度后与反比例函数y=﹣的图象交于A,B两点,且点A,B关于原点对称,则一次函数y=﹣2x+m的特征数是( )
A.[2,3] B.[2,﹣3] C.[﹣2,3] D.[﹣2,﹣3]
8. 规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
9.定义:[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[m,1﹣m,2﹣m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当x>时,y随x的增大而减小.其中所有正确结论的序号是 .
10.我们规定:若=(x1,y1),=(x2,y2),则 =x1x2+y1y2.例如=(1,3),=(2,4),则 =1×2+3×4=2+12=14.已知=(x+1,x﹣1),=(x﹣3,4),且﹣2≤x≤3,则 的最大值是 .
11.规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
12.若把第n个位置上的数记为xn,则称x1,x2,x3,…,xn有限个有序放置的数为一个数列A.定义数列A的“伴生数列”B是:y1,y2,y3,…,yn,其中yn是这个数列中第n个位置上的数,n=1,2,…,k且yn=并规定x0=xn,xn+1=x1.如果数列A只有四个数,且x1,x2,x3,x4依次为3,1,2,1,则其“伴生数列”B是 .
13.定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.
求证:四边形ABCD是等补四边形;
探究:
(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.
运用:
(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,求DF的长.
14. 在平面直角坐标系中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦(分别为点A,B的对应点),线段长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB到⊙O的长度为1的弦和,则这两条弦的位置关系是 ;在点中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线上,记线段AB到⊙O的“平移距离”为,求的最小值;
(3)若点A的坐标为,记线段AB到⊙O的“平移距离”为,直接写出的取值范围.
15.定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,∥,,过点D作BD垂线交BC的延长线于点E,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形内接于⊙O中,.求⊙O的半径.
16.在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如(1,1),(2021,2021)…都是“雁点”.
(1)求函数y=图象上的“雁点”坐标;
(2)若抛物线y=ax2+5x+c上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当a>1时.
①求c的取值范围;
②求∠EMN的度数;
(3)如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左侧),P是抛物线y=﹣x2+2x+3上一点,连接BP,以点P为直角顶点,构造等腰Rt△BPC,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.
17.已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中距”.
(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 .
(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.
18.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,垂美四边形ABCD的对角线AC,BD交于点O.猜想:AB2+CD2与AD2+BC2有什么关系?并证明你的猜想.
(3)解决问题:如图3,分别以Rt△
ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE,BG,GE.已知AC=4,AB=5,求GE的长.
专题12 新定义型数学中考问题(解析版)
1. 我们发现:,,,…,,一般地,对于正整数,,如果满足时,称为一组完美方根数对.如上面是一组完美方根数对.则下面4个结论:①是完美方根数对;②是完美方根数对;③若是完美方根数对,则;④若是完美方根数对,则点在抛物线上.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】根据定义逐项分析判断即可.
,
是完美方根数对;
故①正确;
不是完美方根数对;
故②不正确;
若是完美方根数对,则
即
解得或
是正整数
则
故③正确;
若是完美方根数对,则
,
即
故④正确
故选C
【点睛】本题考查了求算术平方根,解一元二次方程,二次函数的定义,理解定义是解题的关键.
2.在实数范围内定义运算“☆”:,例如:.如果,则的值是( ).
A. B. 1 C. 0 D. 2
【答案】C
【解析】本题考查了实数的计算,一元一次方程的解法,本题的关键是能看明白题目意思,根据新定义的运算规则求解即可
根据题目中给出的新定义运算规则进行运算即可求解.
由题意知:,
又,
∴,
∴.
3.定义新运算“ ”,规定:a b=a﹣2b.若关于x的不等式x m>3的解集为x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
【答案】B
【解析】根据定义新运算的法则得出不等式,解不等式;根据解集列方程即可.
∵a b=a﹣2b,
∴x m═x﹣2m.
∵x m>3,
∴x﹣2m>3,
∴x>2m+3.
∵关于x的不等式x m>3的解集为x>﹣1,
∴2m+3=﹣1,
∴m=﹣2.
4.对于任意的有理数a,b,如果满足+=,那么我们称这一对数a,b为“相随数对”
,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]=( )
A.﹣2 B.﹣1 C.2 D.3
【答案】A
【解析】根据(m,n)是“相随数对”得出9m+4n=0,再将原式化成9m+4n﹣2,最后整体代入求值即可.
∵(m,n)是“相随数对”,
∴+=,
∴=,
即9m+4n=0,
∴3m+2[3m+(2n﹣1)]
=3m+2[3m+2n﹣1]
=3m+6m+4n﹣2
=9m+4n﹣2
=0﹣2
=﹣2,
5.定义一种运算:,则不等式的解集是( )
A. 或 B.
C. 或 D. 或
【答案】C
【解析】由新定义得或,
解得或
6.定义a b=2a+,则方程3 x=4 2的解为( )
A.x= B.x= C.x= D.x=
【答案】B
【解析】利用题中的新定义化简已知等式,求出解即可得到x的值.
根据题中的新定义得:
3 x=2×3+,
4 2=2×4+,
∵3 x=4 2,
∴2×3+=2×4+,
解得:x=,
经检验,x=是分式方程的根.
7.定义:一次函数y=ax+b的特征数为[a,b],若一次函数y=﹣2x+m的图象向上平移3个单位长度后与反比例函数y=﹣的图象交于A,B两点,且点A,B关于原点对称,则一次函数y=﹣2x+m的特征数是( )
A.[2,3] B.[2,﹣3] C.[﹣2,3] D.[﹣2,﹣3]
【答案】D
【解析】将一次函数y=﹣2x+m的图像向上平移3个单位长度后,得到解析式y=﹣2x+m+3,联立一次函数与反比例函数解析式,得到关于x的一元二次方程,设A(x1,0),B(x2,0),所以x1与x2是一元二次方程的两根,根据根与系数关系,得到,又A,B两点关于原点对称,所以x1+x2=0,则,得到m=﹣3,根据定义,得到一次函数y=﹣2x+m的特征数是[﹣2,﹣3].
解:将一次函数y=﹣2x+m向上平移3个单位长度后得到y=﹣2x+m+3,
设A(x1,0),B(x2,0),
联立,
∴2x2﹣(m+3)x﹣3=0,
∵x1和x2是方程的两根,
∴,
又∵A,B两点关于原点对称,
∴x1+x2=0,
∴,
∴m=﹣3,
根据定义,一次函数y=﹣2x+m的特征数是[﹣2,﹣3],
故选:D.
8. 规定:两个函数,的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数与的图象关于y轴对称,则这两个函数互为“Y函数”.若函数(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为______.
【答案】或
【解析】分两种情况,根据关于y轴对称的图形的对称点的坐标特点,即可求得.
函数(k为常数)的“Y函数”图象与x轴只有一个交点,
函数(k为常数)的图象与x轴也只有一个交点,
当k=0时,函数解析为,它的“Y函数”解析式为,它们的图象与x轴只有一个交点,
当时,此函数是二次函数,
它们的图象与x轴都只有一个交点,
它们的顶点分别在x轴上,
,得,
故k+1=0,解得k=-1,
故原函数的解析式为,
故它的“Y函数”解析式为,
故答案为:或.
【点睛】本题考查了新定义,二次函数图象与x轴的交点问题,坐标与图形变换-轴对称,求一次函数及二次函数的解析式,理解题意和采用分类讨论的思想是解决本题的关键.
9.定义:[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[m,1﹣m,2﹣m]的二次函数的一些结论:①当m=1时,函数图象的对称轴是y轴;②当m=2时,函数图象过原点;③当m>0时,函数有最小值;④如果m<0,当x>时,y随x的增大而减小.其中所有正确结论的序号是 .
【答案】①②③.
【解析】根据特征数的定义,写出二次函数的表达式为y=mx2+(1﹣m)x+2﹣m.①写出对称轴方程后把m=1代入即可判断;②把m=2代入即可判断;③根据开口方向即可判断;④根据对称轴,开口方向,增减性即可判断.
由特征数的定义可得:特征数为[m,1﹣m,2﹣m]的二次函数的表达式为y=mx2+(1﹣m)x+2﹣m.
∵此抛物线的的对称轴为直线x===,
∴当m=1时,对称轴为直线x=0,即y轴.故①正确;
∵当m=2时,此二次函数表达式为y=2x2﹣x,令x=0,则y=0,
∴函数图象过原点,故②正确;
∵当m>0时,二次函数图象开口向上,函数有最小值,故③正确;
∵m<0,
∴对称轴x==,抛物线开口向下,
∴在对称轴的右侧,y随x的增大而减小.
即x>时,y随x的增大而减小.
故④错误.故答案为:①②③.
10.我们规定:若=(x1,y1),=(x2,y2),则 =x1x2+y1y2.例如=(1,3),=(2,4),则 =1×2+3×4=2+12=14.已知=(x+1,x﹣1),=(x﹣3,4),且﹣2≤x≤3,则 的最大值是 .
【答案】8.
【解析】根据平面向量的新定义运算法则,列出关于x的二次函数,根据二次函数最值的求法解答即可.
根据题意知: =(x+1)(x﹣3)+4(x﹣1)=(x+1)2﹣8.
因为﹣2≤x≤3,
所以当x=3时, =(3+1)2﹣8=8.
即 的最大值是8.
11.规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°
后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
【答案】(1)B;(2)(1)(3)(5);(3)C;(4)见解析
【解析】(1)根据旋转对称图形的定义进行判断;
(2)先分别求每一个图形中的旋转角,然后再进行判断;
(3)根据旋转对称图形的定义进行判断;
(4)利用旋转对称图形的定义进行设计.
解:(1)矩形、正五边形、菱形、正六边形都是旋转对称图形,但正五边形不是中心对称图形,
故选:B.
(2)是旋转对称图形,且有一个旋转角是60度的有(1)(3)(5).
故答案为:(1)(3)(5).
(3)①中心对称图形,旋转180°一定会和本身重合,是旋转对称图形;故命题①正确;
②等腰三角形绕一个定点旋转一定的角度α(0°<α≤180°)后,不一定能与自身重合,只有等边三角形是旋转对称图形,故②不正确;
③圆具有旋转不变性,绕圆心旋转任意角度一定能与自身重合,是旋转对称图形;故命题③正确;
即命题中①③正确,
故选:C.
(4)图形如图所示:
【点拨】考查旋转对称图形,中心对称图形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
12.若把第n个位置上的数记为xn,则称x1,x2,x3,…,xn有限个有序放置的数为一个数列A.定义数列A的“伴生数列”B是:y1,y2,y3,…,yn,其中yn是这个数列中第n个位置上的数,n=1,2,…,k且yn=并规定x0=xn,xn+1=x1.如果数列A只有四个数,且x1,x2,x3,x4依次为3,1,2,1,则其“伴生数列”B是 .
【答案】0,1,0,1.
【解析】根据“伴生数列”的定义依次取n=1,2,3,4,求出对应的yn即可.
当n=1时,x0=x4=1=x2,
∴y1=0,
当n=2时,x1≠x3,
∴y2=1,
当n=3时,x2=x4,
∴y3=0,
当n=4时,x3≠x5=x1,
∴y4=1,
∴“伴生数列”B是:0,1,0,1,
故答案为0,1,0,1.
13.定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.
求证:四边形ABCD是等补四边形;
探究:
(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.
运用:
(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,求DF的长.
【答案】见解析。
【解析】(1)由圆内接四边形互补可知∠A+∠C=180°,∠ABC+∠ADC=180°,再证AD=CD,即可根据等补四边形的定义得出结论;
(2)过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,证△ABE≌△ADF,得到AE=AF,根据角平分线的判定可得出结论;
(3)连接AC,先证∠EAD=∠BCD,推出∠FCA=∠FAD,再证△ACF∽△DAF,利用相似三角形对应边的比相等可求出DF的长.
【解答】(1)证明:∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,∠ABC+∠ADC=180°,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴,
∴AD=CD,
∴四边形ABCD是等补四边形;
(2)AD平分∠BCD,理由如下:
如图2,过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,
则∠AEB=∠AFD=90°,
∵四边形ABCD是等补四边形,
∴∠B+∠ADC=180°,
又∠ADC+∠ADF=180°,
∴∠B=∠ADF,
∵AB=AD,
∴△ABE≌△ADF(AAS),
∴AE=AF,
∴AC是∠BCF的平分线,即AC平分∠BCD;
(3)如图3,连接AC,
∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180°,
又∠BAD+∠EAD=180°,
∴∠EAD=∠BCD,
∵AF平分∠EAD,
∴∠FAD=∠EAD,
由(2)知,AC平分∠BCD,
∴∠FCA=∠BCD,
∴∠FCA=∠FAD,
又∠AFC=∠DFA,
∴△ACF∽△DAF,
∴,
即,
∴DF=5﹣5.
【点评】考查新定义等补四边形,圆的有关性质,全等三角形的判定与性质,角平分线的判定,相似三角形的判定与性质等,解题关键是要能够通过自主学习来进行探究,运用等.
14. 在平面直角坐标系中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦(分别为点A,B的对应点),线段长度的最小值称为线段AB到⊙O的“平移距离”.
(1)如图,平移线段AB到⊙O的长度为1的弦和,则这两条弦的位置关系是 ;在点中,连接点A与点 的线段的长度等于线段AB到⊙O的“平移距离”;
(2)若点A,B都在直线上,记线段AB到⊙O的“平移距离”为,求的最小值;
(3)若点A的坐标为,记线段AB到⊙O的“平移距离”为,直接写出的取值范围.
【答案】(1)平行,P3;(2);(3)
【解析】(1)根据圆的性质及“平移距离”的定义填空即可;
(2)过点O作OE⊥AB于点E,交弦CD于点F,分别求出OE、OF的长,由得到的最小值;
(3)线段AB的位置变换,可以看作是以点A为圆心,半径为1的圆,只需在⊙O内找到与之平行,且长度为1的弦即可.平移距离的最大值即点A,B点的位置,由此得出的取值范围.
【详解】解:(1)平行;P3;
(2)如图,线段AB在直线上,平移之后与圆相交,得到的弦为CD,CD∥AB,过点O作OE⊥AB于点E,交弦CD于点F,OF⊥CD,令,直线与x轴交点为(-2,0),直线与x轴夹角为60°,∴.
由垂径定理得:,
∴;
(3)线段AB的位置变换,可以看作是以点A为圆心,半径为1的圆,只需在⊙O内找到与之平行,且长度为1的弦即可;
点A到O的距离为.
如图,平移距离的最小值即点A到⊙O的最小值:;
平移距离的最大值线段是下图AB的情况,即当A1,A2关于OA对称,且A1B2⊥A1A2且A1B2=1时.∠B2A2A1=60°,则∠OA2A1=30°,
∵OA2=1,∴OM=, A2M=,
∴MA=3,AA2= ,
∴的取值范围为:.
【点睛】本题考查圆的基本性质及与一次函数的综合运用,熟练掌握圆的基本性质、点与圆的位置关系、直线与圆的位置关系是解题的关键.
15.定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是____________(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形中,∥,,过点D作BD垂线交BC的延长线于点E,且,证明:四边形是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形内接于⊙O中,.求⊙O的半径.
【答案】(1)④;(2)证明过程见解析;③4
【解析】(1)根据垂等四边形的性质对每个图形判断即可;
(2)根据已知条件可证明四边形ACED是平行四边形,即可得到AC=DE,再根据等腰直角三角形的性质即可得到结果;
(3)过点O作,根据面积公式可求得BD的长,根据垂径定理即可得到答案.
【详解】(1)①平行四边形的对角线互相平分但不垂直和相等,故不是;②矩形对角线相等但不垂直;③菱形的对角线互相垂直但不相等;④正方形的对角线互相垂直且相等,故正方形是垂等四边形;
(2)∵,,
∴AC∥DE,
又∵∥,
∴四边形ADEC是平行四边形,
∴AC=DE,
又∵,
∴△BDE是等腰直角三角形,
∴BD=DE,
∴BD=AC,
∴四边形是垂等四边形.
(3)如图,过点O作,
∵四边形是垂等四边形,
∴AC=BD,
又∵垂等四边形的面积是24,,根据垂等四边形的面积计算方法得:
,
又∵,
∴,
设半径为r,根据垂径定理可得:
在△ODE中,OD=r,DE=,
∴,
∴的半径为4.
【点睛】本题主要考查了四边形性质与圆的垂径定理应用,准确理解新定义的垂等四边形的性质是解题的关键.
16.在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如(1,1),(2021,2021)…都是“雁点”.
(1)求函数y=图象上的“雁点”坐标;
(2)若抛物线y=ax2+5x+c上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当a>1时.
①求c的取值范围;
②求∠EMN的度数;
(3)如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左侧),P是抛物线y=﹣x2+2x+3上一点,连接BP,以点P为直角顶点,构造等腰Rt△BPC,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】见解析。
【解析】(1)由题意得:x=,解得x=±2,即可求解;
(2)①由△=25﹣4ac=0,即ac=4,即可求解;
②求出点M的坐标为(﹣,0)、点E的坐标为(﹣,﹣),即可求解;
(3)证明△CMP≌△PNB(AAS),则PM=BN,CM=PN,即可求解.
解:(1)由题意得:x=,解得x=±2,
当x=±2时,y==±2,
故“雁点”坐标为(2,2)或(﹣2,﹣2);
(2)①∵“雁点”的横坐标与纵坐标相等,
故“雁点”的函数表达式为y=x,
∵物线y=ax2+5x+c上有且只有一个“雁点”E,
则ax2+5x+c=x,
则△=25﹣4ac=0,即ac=4,
∵a>1,
故c<4;
②∵ac=4,则ax2+5x+c=0为ax2+5x+=0,
解得x=﹣或﹣,即点M的坐标为(﹣,0),
由ax2+5x+c=x,ac=4,
解得x=﹣,即点E的坐标为(﹣,﹣),
故点E作EH⊥x轴于点H,
则HE=,MH=xE﹣xM=﹣﹣(﹣)==HE,
故∠EMN的度数为45°;
(3)存在,理由:
由题意知,点C在直线y=x上,故设点C的坐标为(t,t),
过点P作x轴的平行线交过点C与y轴的平行线于点M,交过点B与y轴的平行线于点N,
设点P的坐标为(m,﹣m2+2m+3),
则BN=﹣m2+2m+3,PN=3﹣m,PM=m﹣t,CM=﹣m2+2m+3﹣t,
∵∠NPB+∠MPC=90°,∠MPC+∠CPM=90°,
∴∠NPB=∠CPM,
∵∠CMP=∠PNB=90°,PC=PB,
∴△CMP≌△PNB(AAS),
∴PM=BN,CM=PN,
即m﹣t=|﹣m2+2m+3|,﹣m2+2m+3﹣t=|3﹣m|,
解得m=1+(舍去)或1﹣或,
故点P的坐标为(,)或(,).
17.已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中距”.
(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是 .
(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.
【答案】见解析。
【分析】(1)猜想:OC=OD.证明Rt△AOC≌Rt△BOD(HL),可得结论.
(2)结论成立.过点O作直线EF∥CD,交BD于点F,延长AC交EF于点E,证明△COE≌DOF(SAS),可得结论.
(3)①结论成立.如图3中,延长CO交BD于点E,证明CO=OE,再利用直角三角形斜边中线的性质解决问题即可.
②结论:AC+BD=OC.利用等边三角形的判定和性质以及全等三角形的性质证明即可.
解:(1)猜想:OC=OD.
理由:如图1中,∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°
在Rt△AOC与Rt△BOD中,
,
∴Rt△AOC≌Rt△BOD(HL),
∴OC=OD,
故答案为:OC=OD;
(2)数量关系依然成立.
理由:过点O作直线EF∥CD,交BD于点F,延长AC交EF于点E,
∵EF∥CD,
∴∠DCE=∠E=∠CDF=90°,
∴四边形CEFD为矩形,
∴∠OFD=90°,CE=DF,
由(1)知,OE=OF,
在△COE与△DOF中,
,
∴△COE≌DOF(SAS),
∴OC=OD;
(3)①结论成立.
理由:如图3中,延长CO交BD于点E,
∵AC⊥CD,BD⊥CD,
∴AC∥BD,
∴∠A=∠B,
∵点O为AB的中点,
∴AO=BO,
又∵∠AOC=∠BOE,
∴△AOC≌△BOE(AAS),
∴CO=CE,
∵∠CDE=90°,
∴OD=OC=OE,
∴OC=OD.
②结论:AC+BD=OC.
理由:如图3中,∵∠COD=60°,OD=OC,
∴△COD是等边三角形,
∴CD=OC,∠OCD=60°,
∵∠CDE=90°,
∴tan60°=,
∴DE=CD,
∴△AOC≌△BOE,
∴AC=BE,
∴AC+BD=BD+BE=DE=CD,
∴AC+BD=OC.
18.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,垂美四边形ABCD的对角线AC,BD交于点O.猜想:AB2+CD2与AD2+BC2有什么关系?并证明你的猜想.
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE,BG,GE.已知AC=4,AB=5,求GE的长.
【答案】见解析.
【解析】(1)连接AC、BD,根据垂直平分线的判定定理证明即可;
(2)根据垂直的定义和勾股定理解答即可;
(3)如图3,连接CG、BE,根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
解:(1)四边形ABCD是垂美四边形.
理由如下:如图2,连接AC、BD,
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)AB2+CD2=AD2+BC2,
理由如下:
如图1中,
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2;
(3)如图3,连接CG、BE,
∵正方形ACFG和正方形ABDE,
∴AG=AC,AB=AE,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
∵∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC===3,
∵CG===4,BE===5,
∴GE2=CG2+BE2﹣CB2=(4)2+(5)2﹣32=73,
∴GE=.
同课章节目录
