2025中考数学复习冲刺之特色微专题巩固_专题15 初中数学重要的定理和公式的推理证明问题(含解析)
文档属性
| 名称 | 2025中考数学复习冲刺之特色微专题巩固_专题15 初中数学重要的定理和公式的推理证明问题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览


文档简介
专题15 初中数学重要的定理和公式的推理证明问题
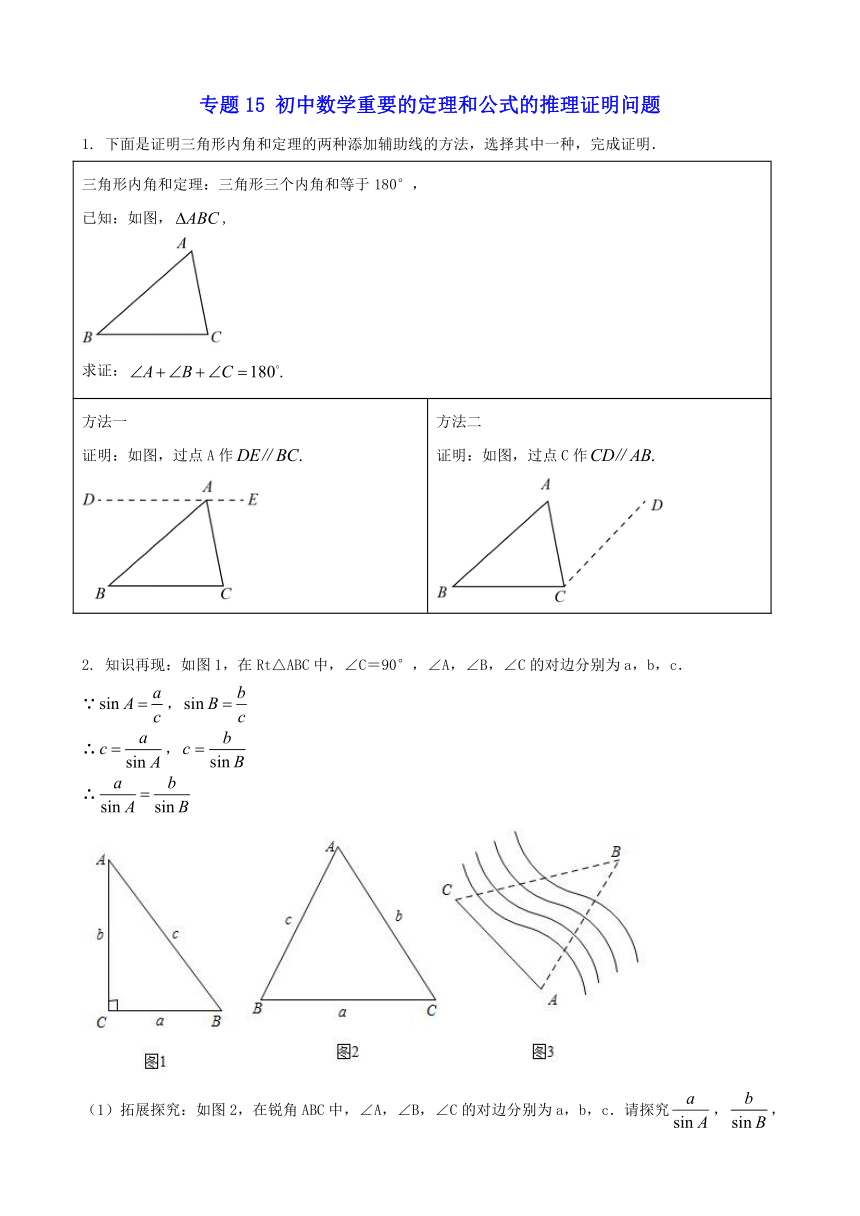
1. 下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°, 已知:如图,, 求证:
方法一 证明:如图,过点A作 方法二 证明:如图,过点C作
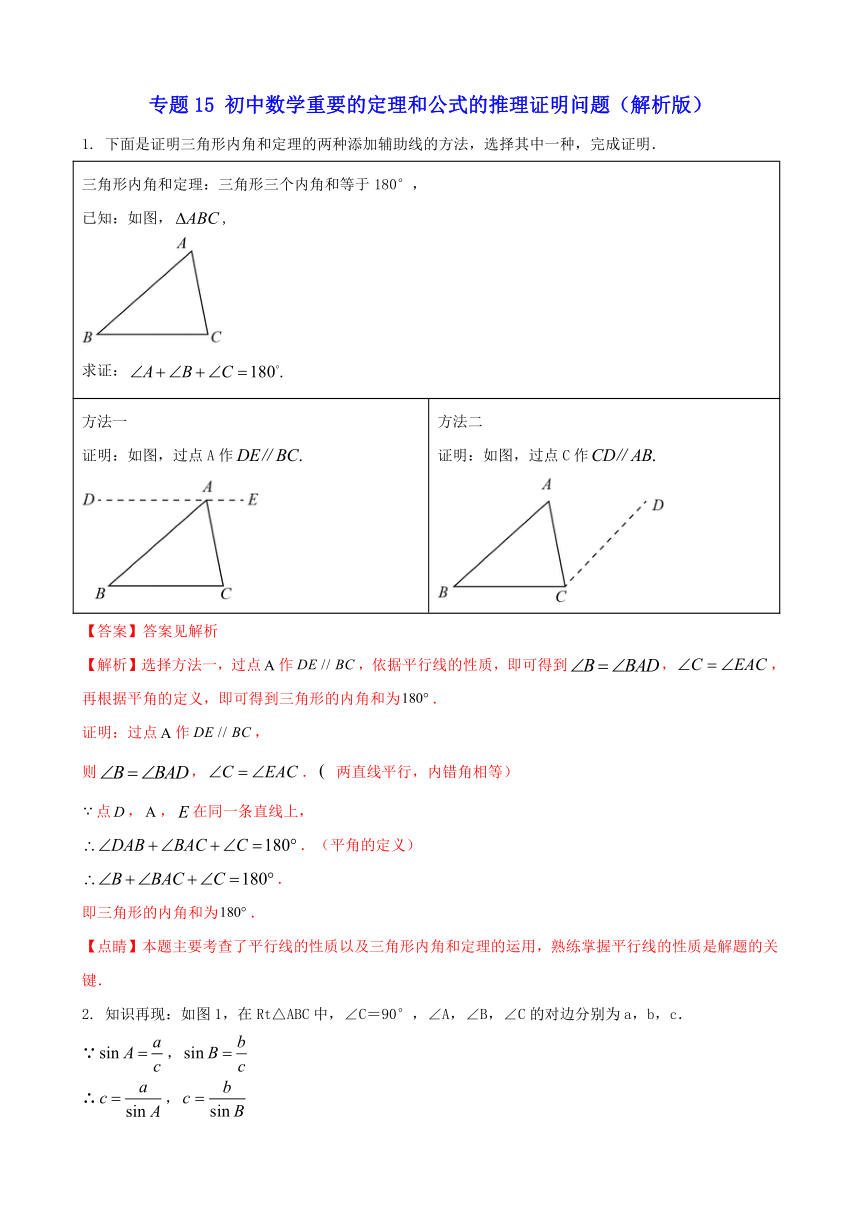
2. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵,
∴,
∴
(1)拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究,,之间的关系,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
3.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图, ∵∠A+∠B+∠ACB=180°(三角形内角和定理), 又∵∠ACD+∠ACB=180°(平角定义), ∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换). ∴∠ACD=∠A+∠B(等式性质).
证法2:如图, ∵∠A=76°,∠B=59°, 且∠ACD=135°(量角器测量所得) 又∵135°=76°+59°(计算所得) ∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
4.用1876年美国第十七任总统加菲尔德Garfield的方法证明勾股定理
专题15 初中数学重要的定理和公式的推理证明问题(解析版)
1. 下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°, 已知:如图,, 求证:
方法一 证明:如图,过点A作 方法二 证明:如图,过点C作
【答案】答案见解析
【解析】选择方法一,过点作,依据平行线的性质,即可得到,,再根据平角的定义,即可得到三角形的内角和为.
证明:过点作,
则,. 两直线平行,内错角相等)
点,,在同一条直线上,
.(平角的定义)
.
即三角形的内角和为.
【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用,熟练掌握平行线的性质是解题的关键.
2. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵,
∴,
∴
(1)拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究,,之间的关系,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
【答案】(1),证明见解析 (2)米
【解析】【分析】拓展研究:作CD⊥AB于点D,AE⊥BC于点E,根据正弦的定义得AE = csinB,
AE= bsin∠BCA,CD= asinB,CD = bsin∠BAC,从而得出结论;
解决问题:由拓展探究知, 代入计算即可.
【小问1详解】
(拓展探究)证明:作CD⊥AB于点D,AC⊥BC于点E.
在RtΔABE中,,
同理:,
.
.
.
.
.
【小问2详解】
(解答问题)解:在ΔABC中,
∴
解得:
答:点A到点B的距离为m.
【点睛】本题主要考查了解直角三角形,对于锐角三角形,利用正弦的定义,得出是解题的关键.
3.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图, ∵∠A+∠B+∠ACB=180°(三角形内角和定理), 又∵∠ACD+∠ACB=180°(平角定义), ∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换). ∴∠ACD=∠A+∠B(等式性质).
证法2:如图, ∵∠A=76°,∠B=59°, 且∠ACD=135°(量角器测量所得) 又∵135°=76°+59°(计算所得) ∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
【答案】B
【解析】依据定理证明的一般步骤进行分析判断即可得出结论.
∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,具有一般性,无需再证明其他形状的三角形,
∴A的说法不正确,不符合题意;
∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,
∴B的说法正确,符合题意;
∵定理的证明必须经过严谨的推理论证,不能用特殊情形来说明,
∴C的说法不正确,不符合题意;
∵定理的证明必须经过严谨的推理论证,与测量次解答数的多少无关,
∴D的说法不正确,不符合题意;
综上,B的说法正确.
故选:B.
4.用1876年美国第十七任总统加菲尔德Garfield的方法证明勾股定理
【答案】见解析。
【解析】以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab/2. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.
∵ RtΔEAD ≌ RtΔCBE,
∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90 ,
∴ ∠AED + ∠BEC = 90 .
∴ ∠DEC = 180 ―90 = 90 .
∴ ΔDEC是一个等腰直角三角形,
它的面积等于c2
又∵ ∠DAE = 90 , ∠EBC = 90 ,
∴ AD∥BC.
∴ ABCD是一个直角梯形,它的面积等于S=(a+b)2……
又因为这个直角梯形的面积等于三个小三角形面积之和,即S= 2×ab+c2……
由得
(a+b)2= 2×ab+c2
化简:.
从而结论得到证明。
1. 下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°, 已知:如图,, 求证:
方法一 证明:如图,过点A作 方法二 证明:如图,过点C作
2. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵,
∴,
∴
(1)拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究,,之间的关系,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
3.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图, ∵∠A+∠B+∠ACB=180°(三角形内角和定理), 又∵∠ACD+∠ACB=180°(平角定义), ∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换). ∴∠ACD=∠A+∠B(等式性质).
证法2:如图, ∵∠A=76°,∠B=59°, 且∠ACD=135°(量角器测量所得) 又∵135°=76°+59°(计算所得) ∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
4.用1876年美国第十七任总统加菲尔德Garfield的方法证明勾股定理
专题15 初中数学重要的定理和公式的推理证明问题(解析版)
1. 下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形内角和定理:三角形三个内角和等于180°, 已知:如图,, 求证:
方法一 证明:如图,过点A作 方法二 证明:如图,过点C作
【答案】答案见解析
【解析】选择方法一,过点作,依据平行线的性质,即可得到,,再根据平角的定义,即可得到三角形的内角和为.
证明:过点作,
则,. 两直线平行,内错角相等)
点,,在同一条直线上,
.(平角的定义)
.
即三角形的内角和为.
【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用,熟练掌握平行线的性质是解题的关键.
2. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵,
∴,
∴
(1)拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究,,之间的关系,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
【答案】(1),证明见解析 (2)米
【解析】【分析】拓展研究:作CD⊥AB于点D,AE⊥BC于点E,根据正弦的定义得AE = csinB,
AE= bsin∠BCA,CD= asinB,CD = bsin∠BAC,从而得出结论;
解决问题:由拓展探究知, 代入计算即可.
【小问1详解】
(拓展探究)证明:作CD⊥AB于点D,AC⊥BC于点E.
在RtΔABE中,,
同理:,
.
.
.
.
.
【小问2详解】
(解答问题)解:在ΔABC中,
∴
解得:
答:点A到点B的距离为m.
【点睛】本题主要考查了解直角三角形,对于锐角三角形,利用正弦的定义,得出是解题的关键.
3.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图, ∵∠A+∠B+∠ACB=180°(三角形内角和定理), 又∵∠ACD+∠ACB=180°(平角定义), ∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换). ∴∠ACD=∠A+∠B(等式性质).
证法2:如图, ∵∠A=76°,∠B=59°, 且∠ACD=135°(量角器测量所得) 又∵135°=76°+59°(计算所得) ∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
【答案】B
【解析】依据定理证明的一般步骤进行分析判断即可得出结论.
∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,具有一般性,无需再证明其他形状的三角形,
∴A的说法不正确,不符合题意;
∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,
∴B的说法正确,符合题意;
∵定理的证明必须经过严谨的推理论证,不能用特殊情形来说明,
∴C的说法不正确,不符合题意;
∵定理的证明必须经过严谨的推理论证,与测量次解答数的多少无关,
∴D的说法不正确,不符合题意;
综上,B的说法正确.
故选:B.
4.用1876年美国第十七任总统加菲尔德Garfield的方法证明勾股定理
【答案】见解析。
【解析】以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab/2. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.
∵ RtΔEAD ≌ RtΔCBE,
∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90 ,
∴ ∠AED + ∠BEC = 90 .
∴ ∠DEC = 180 ―90 = 90 .
∴ ΔDEC是一个等腰直角三角形,
它的面积等于c2
又∵ ∠DAE = 90 , ∠EBC = 90 ,
∴ AD∥BC.
∴ ABCD是一个直角梯形,它的面积等于S=(a+b)2……
又因为这个直角梯形的面积等于三个小三角形面积之和,即S= 2×ab+c2……
由得
(a+b)2= 2×ab+c2
化简:.
从而结论得到证明。
同课章节目录
