2025中考数学复习冲刺之特色微专题巩固_专题14 尺规作图问题大全(含解析)
文档属性
| 名称 | 2025中考数学复习冲刺之特色微专题巩固_专题14 尺规作图问题大全(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 20:29:12 | ||
图片预览




文档简介
专题14 尺规作图问题大全
1. 如图,已知直线AB和AB上的一点C,过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以为半径作弧,两弧交于点F;
第三步:作直线CF,直线CF即为所求.
下列关于的说法正确的是( )
A. ≥ B. ≤ C. D.
2.如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )
A.AN=NC B.AN=BN C.MN=BC D.BN平分∠ABC
3.如图,已知△ABC.
(1)以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N.
(2)分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BAC的内部相交于点P.
(3)作射线AP交BC于点D.
(4)分别以A,D为圆心,以大于AD的长为半径画弧,两弧相交于G,H两点.
(5)作直线GH,交AC,AB分别于点E,F.
依据以上作图,若AF=2,CE=3,BD=,则CD的长是( )
A. B.1 C. D.4
4.已知: AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3),则点A的坐标为( )
A.(,3) B.(3﹣,3) C.(﹣,3) D.(2﹣,3)
5.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,按下列步骤作图:
步骤1:以点A为圆心,小于AC的长为半径作弧分别交AC、AB于点D、E.
步骤2:分别以点D、E为圆心,大于DE的长为半径作弧,两弧交于点M.
步骤3:作射线AM交BC于点F.
则AF的长为( )
A.6 B.3 C.4 D.6
6.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20° B.30° C.40° D.50°
7.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
8.如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交AB、AC于点M、N;再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
9.如图,已知线段AB长为4.现按照以下步骤作图:
①分别以点A,B为圆心,大于AB长为半径画弧,两弧分别相交于点E,F;
②过E,F两点作直线,与线段AB相交于点O.
则AO的长为 .
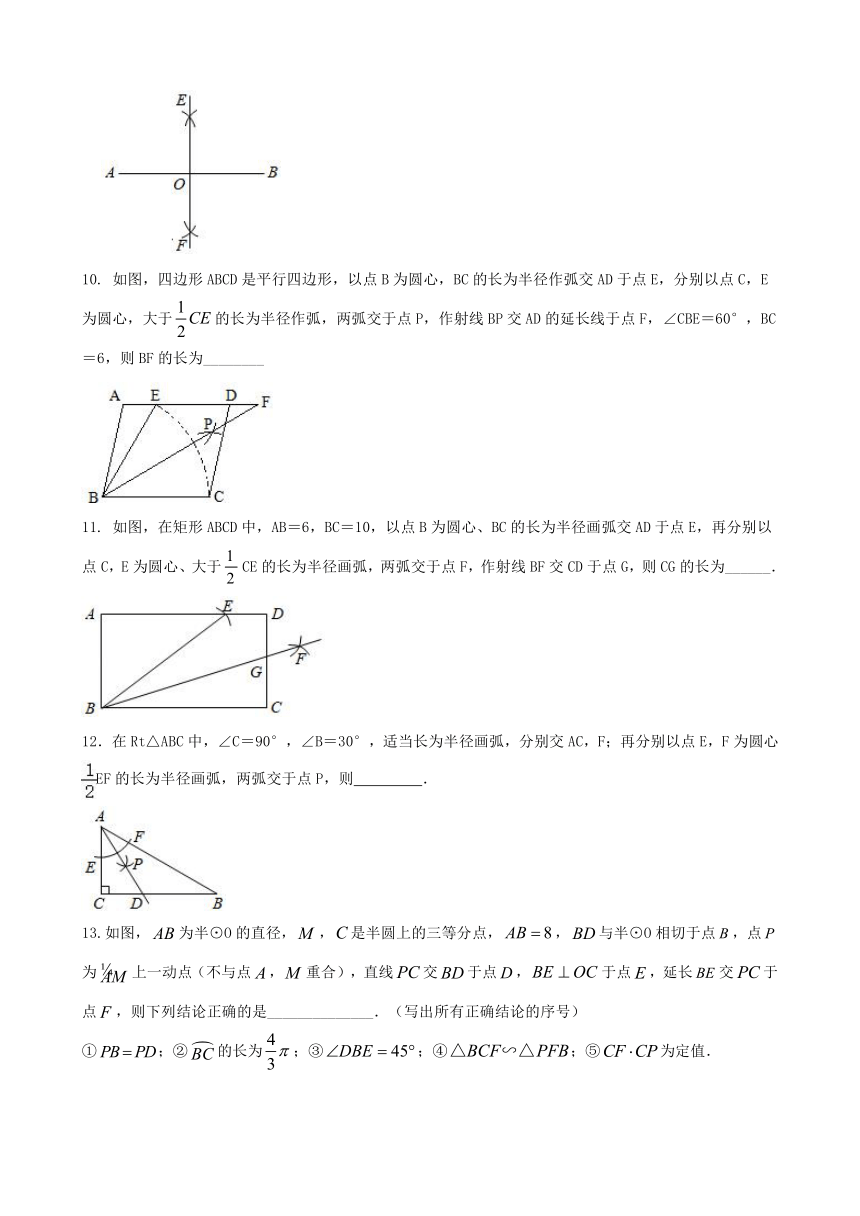
10. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,分别以点C,E为圆心,大于的长为半径作弧,两弧交于点P,作射线BP交AD的延长线于点F,∠CBE=60°,BC=6,则BF的长为________
11. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心、BC的长为半径画弧交AD于点E,再分别以点C,E为圆心、大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为______.
12.在Rt△ABC中,∠C=90°,∠B=30°,适当长为半径画弧,分别交AC,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点P,则 .
13.如图,为半⊙O的直径,,是半圆上的三等分点,,与半⊙O相切于点,点为上一动点(不与点,重合),直线交于点,于点,延长交于点,则下列结论正确的是______________.(写出所有正确结论的序号)
①;②的长为;③;④;⑤为定值.
14.如图,已知直线l1∥l2,直线l3分别与l1、l2交于点A、B.请用尺规作图法,在线段AB上求作一点P,使点P到l1、l2的距离相等.(保留作图痕迹,不写作法)
15.已知:如图,ABC为锐角三角形,AB=BC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP=.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC( )(填推理依据)
∴∠ABP=∠BAC
16.如图,在中,是边上一点,且.
(1)尺规作图(保留作图痕迹,不写作法)
①作的角平分线交于点;
②作线段的垂直平分线交于点.
(2)连接,直接写出线段和的数量关系及位置关系.
17. 如图,已知线段,垂足为a.
(1)求作四边形,使得点B,D分别在射线上,且,,;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设P,Q分别为(1)中四边形的边的中点,求证:直线相交于同一点.
18.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使△ADE∽△ACB.
19. 如图,四边形ABCD中,,,连接AC.
(1)求证:≌;
(2)尺规作图:过点C作AB的垂线,垂足为不要求写作法,保留作图痕迹;
(3)在(2)的条件下,已知四边形ABCD的面积为20,,求CE的长.
20.如图,已知Rt△ABC中,∠C=90°.
(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).
①作∠BAC的角平分线AD,交BC于点D;
②作线段AD的垂直平分线EF与AB相交于点O;
③以点O为圆心,以OD长为半径画圆,交边AB于点M.
(2)在(1)的条件下,求证:BC是⊙O的切线;
(3)若AM=4BM,AC=10,求⊙O的半径.
21. 已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
专题14 尺规作图问题大全(解析版)
1. 如图,已知直线AB和AB上的一点C,过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以为半径作弧,两弧交于点F;
第三步:作直线CF,直线CF即为所求.
下列关于的说法正确的是( )
A. ≥ B. ≤ C. D.
【答案】C
【解析】根据过直线外一点作已知直线的垂线的步骤,结合三角形三边关系判断即可.
由作图可知,分别以点和点为圆心,以为半径作弧,两弧交于点,此时.
【点睛】本题考查作图基本作图,解题的关键是理解题意,灵活运用所学知识解决问题.
2.如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )
A.AN=NC B.AN=BN C.MN=BC D.BN平分∠ABC
【答案】B
【解析】直接利用线段垂直平分线的性质求解.
由作法得DE垂直平分AB,
∴NA=NB.
3.如图,已知△ABC.
(1)以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N.
(2)分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BAC的内部相交于点P.
(3)作射线AP交BC于点D.
(4)分别以A,D为圆心,以大于AD的长为半径画弧,两弧相交于G,H两点.
(5)作直线GH,交AC,AB分别于点E,F.
依据以上作图,若AF=2,CE=3,BD=,则CD的长是( )
A. B.1 C. D.4
【答案】B
【解析】利用作法得AD平分∠BAC,EF垂直平分AD,所以∠EAD=∠FAD,EA=ED,FA=FD,再证明四边形AEDF为菱形得到AE=AF=2,然后利用平行线分线段成比例定理计算CD的长.
解:由作法得AD平分∠BAC,EF垂直平分AD,
∴∠EAD=∠FAD,EA=ED,FA=FD,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠FAD=∠EDA,
∴DE∥AF,
同理可得AE∥DF,
∴四边形AEDF为平行四边形,
而EA=ED,
∴四边形AEDF为菱形,
∴AE=AF=2,
∵DE∥AB,
∴=,即=,
∴CD=.
4.已知: AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3),则点A的坐标为( )
A.(,3) B.(3﹣,3) C.(﹣,3) D.(2﹣,3)
【答案】A
【解析】利用基本作图得到∠AOF=∠COF,再根据平行四边形的性质得到AD∥OC,接着证明∠AOF=∠AFO得到OA=AF,设AF交y轴于M,如图,设A(t,3),则AM=﹣t,AO=AF=﹣t+2,利用勾股定理得到t2+32=(﹣t+2)2,然后解方程求出t即可得到A点坐标.
解:由作法得OE平分∠AOC,则∠AOF=∠COF,
∵四边形AOCD为平行四边形,
∴AD∥OC,
∴∠AFO=∠COF,
∴∠AOF=∠AFO,
∴OA=AF,
设AF交y轴于M,如图,
∵F(2,3),
∴MF=2,OM=3,
设A(t,3),
∴AM=﹣t,AO=AF=﹣t+2,
在Rt△OAM中,t2+32=(﹣t+2)2,解得t=﹣,
∴A(﹣,3).
故选:A.
5.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,按下列步骤作图:
步骤1:以点A为圆心,小于AC的长为半径作弧分别交AC、AB于点D、E.
步骤2:分别以点D、E为圆心,大于DE的长为半径作弧,两弧交于点M.
步骤3:作射线AM交BC于点F.
则AF的长为( )
A.6 B.3 C.4 D.6
【答案】B
【解析】利用基本作图得到AF平分∠BAC,过F点作FH⊥AB于H,如图,根据角平分线的性质得到FH=FC,再根据勾股定理计算出AC=6,设CF=x,则FH=x,然后利用面积法得到×10 x+×6 x=×6×8,解得x=3,最后利用勾股定理计算AF的长.
解:由作法得AF平分∠BAC,
过F点作FH⊥AB于H,如图,
∵AF平分∠BAC,FH⊥AB,FC⊥AC,
∴FH=FC,
在△ABC中,∵∠C=90°,AB=10,BC=8,
∴AC==6,
设CF=x,则FH=x,
∵S△ABF+S△ACF=S△ABC,
∴×10 x+×6 x=×6×8,解得x=3,
在Rt△ACF中,AF===3.
故选:B.
6.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20° B.30° C.40° D.50°
【答案】B
【解析】由作法得OD=OC,DO=DE,利用等腰三角形的性质和三角形内角和计算出∠OCD=∠ODC=70°,∠DEO=∠DOE=40°,然后利用三角形外角性质计算∠CDE的度数.
解:由作法得OD=OC,DO=DE,
∵OD=OC,
∴∠OCD=∠ODC=(180°﹣∠COD)=×(180°﹣40°)=70°,
∵DO=DE,
∴∠DEO=∠DOE=40°,
∵∠OCD=∠CDE+∠DEC,
∴∠CDE=70°﹣40°=30°.
7.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
【答案】A
【解析】利用基本作图得BD平分∠ABC,过D点作DE⊥AB于E,如图,根据角平分线的性质得到则DE=DC,再利用勾股定理计算出AC=8,然后利用面积法得到 DE×10+ CD×6=×6×8,最后解方程即可.
解:由作法得BD平分∠ABC,
过D点作DE⊥AB于E,如图,则DE=DC,
在Rt△ABC中,AC===8,
∵S△ABD+S△BCD=S△ABC,
∴ DE×10+ CD×6=×6×8,
即5CD+3CD=24,
∴CD=3.
故选:A.
8.如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交AB、AC于点M、N;再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
【答案】C
【解析】根据题意判断AD是∠BAC的角平分线,可知C正确,根据重心和外心定义可知B、D选项错误,根据三角形任意两边之和大于第三边可知A错误.
由题可知AD是∠BAC的角平分线,
A、在△ABD中,AD+BD>AB,故选项A错误,不符合题意;
B、△ABC的重心是三条中线的交点,故选项B错误,不符合题意;
C、∵AD是∠BAC的角平分线,∴∠BAD=∠CAD,故选项C正确,符合题意;
D、△ABC的外心是三边中垂线的交点,故选项D错误,不符合题意.
9.如图,已知线段AB长为4.现按照以下步骤作图:
①分别以点A,B为圆心,大于AB长为半径画弧,两弧分别相交于点E,F;
②过E,F两点作直线,与线段AB相交于点O.
则AO的长为 .
【答案】2
【解析】直接利用基本作图方法得出EF垂直平分AB,即可得出答案.
由基本作图方法可得:EF垂直平分AB,
∵AB=4,
∴AO=AB=2.
10. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,分别以点C,E为圆心,大于的长为半径作弧,两弧交于点P,作射线BP交AD的延长线于点F,∠CBE=60°,BC=6,则BF的长为________
【答案】
【解析】利用基本作图得到,平分,则,再根据平行四边形的性质和平行线的性质证明,所以,过点作于,如图,则,然后利用30°的三角函数值即可求出,从而得到的长.
【详解】由作法得,平分,
又∵∠CBE=60°,
,
四边形为平行四边形,
,
,
,
,
如图,过点作于,
∵,,
∴,
在中,,
,
.
故答案为:.
【点睛】本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的性质、等腰三角形的判定及性质以及解直角三角形的应用.
11. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心、BC的长为半径画弧交AD于点E,再分别以点C,E为圆心、大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为______.
【答案】
【解析】根据作图过程可得BF是∠EBC的平分线,然后证明△EBG≌△CBG,再利用勾股定理即可求出CG的长.
如图,连接EG,
根据作图过程可知:BF是∠EBC的平分线,
∴∠EBG=∠CBG,
在△EBG和△CBG中,
,
∴△EBG≌△CBG(SAS),
∴GE=GC,∠BEG=∠C=90°,
在Rt△ABE中,AB=6,BE=BC=10,
∴AE==8,
∴DE=AD﹣AE=10﹣8=2,
Rt△DGE中,DE=2,DG=DC﹣CG=6﹣CG,EG=CG,
∴EG2﹣DE2=DG2
∴CG2﹣22=(6﹣CG)2,
解得CG=.
故答案为:.
【点睛】本题考查了矩形的性质,作图-基本作图,解决本题的关键是掌握矩形的性质.
12.在Rt△ABC中,∠C=90°,∠B=30°,适当长为半径画弧,分别交AC,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点P,则 .
【答案】BD=3CD.
【解析】证明AD=DB=2CD,可得结论.
∵∠C=90°,∠B=30°,
∴∠CAB=90°﹣30°=60°,
由作图可知AD平分∠CAB,
∴∠CAD=∠BAD=30°,
∴AD=2CD,
∵∠BAD=∠B=30°,
∴AD=DB,
∴BD=3CD,故答案为:BD=3CD.
13.如图,为半⊙O的直径,,是半圆上的三等分点,,与半⊙O相切于点,点为上一动点(不与点,重合),直线交于点,于点,延长交于点,则下列结论正确的是______________.(写出所有正确结论的序号)
①;②的长为;③;④;⑤为定值.
【答案】②⑤
【解析】①先根据圆的切线的性质可得,再根据半圆上的三等分点可得,然后根据圆周角定理可得,最后假设,根据角的和差、三角形的外角性质可得,这与点为上一动点相矛盾,由此即可得;
②根据弧长公式即可得;
③先根据等边三角形的性质可得,再根据角的和差即可得;
④先根据三角形的外角性质可得,从而可得对应角与不可能相等,由此即可得;⑤先根据相似三角形的判定与性质可得,从而可得,再根据等边三角形的性质可得,由此即可得.
【详解】如图,连接OP
与半⊙O相切于点
是半圆上的三等分点
是等边三角形
由圆周角定理得:
假设,则
又点为上一动点
不是一个定值,与相矛盾
即PB与PD不一定相等,结论①错误
则的长为,结论②正确
是等边三角形,
,则结论③错误
,即对应角与不可能相等
与不相似,则结论④错误
在和中,
,即
又是等边三角形,
即为定值,结论⑤正确
综上,结论正确的是②⑤
故答案为:②⑤.
【点睛】本题考查了圆周角定理、圆的切线的性质、弧长公式、相似三角形的判定与性质、等边三角形的判定与性质等知识点,较难的题①,先假设结论成立,再推出矛盾点是解题关键.
14.如图,已知直线l1∥l2,直线l3分别与l1、l2交于点A、B.请用尺规作图法,在线段AB上求作一点P,使点P到l1、l2的距离相等.(保留作图痕迹,不写作法)
【答案】见解析。
【解析】作线段AB的垂直平分线得到线段AB的中点,则中点为P点.
如图,点P为所作.
15.已知:如图,ABC为锐角三角形,AB=BC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP=.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC( )(填推理依据)
∴∠ABP=∠BAC
【答案】(1)见解析;(2)∠BPC,在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半
【解析】(1)按照作法的提示,逐步作图即可;
(2)利用平行线的性质证明: 再利用圆的性质得到:∠BPC=∠BAC,从而可得答案.
【详解】(1)依据作图提示作图如下:
(2)证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC(在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半. )(填推理依据)
∴∠ABP=∠BAC
故答案为:∠BPC;在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半.
【点睛】本题考查的是作图中复杂作图,同时考查了平行线的性质,圆的基本性质:在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半.掌握以上知识是解题的关键.
16.如图,在中,是边上一点,且.
(1)尺规作图(保留作图痕迹,不写作法)
①作的角平分线交于点;
②作线段的垂直平分线交于点.
(2)连接,直接写出线段和的数量关系及位置关系.
【答案】(1)①作图见解析,②作图见解析;(2)
【解析】(1)①根据角平分线的作图方法直接作图即可;②根据垂直平分线的作图方法直接作图即可;
(2)据等腰三角形的性质与垂直平分线的定义证明是的中位线,根据中位线的性质可得答案.
【详解】(1)如图,①即为所求作的的角平分线,
②过的垂线是所求作的线段的垂直平分线.
(2)如图,连接,
平分
由作图可知:
是的中位线,
【点睛】本题考查的是角平分线与垂直平分线的尺规作图,同时考查了三角形的中位线的性质,掌握以上知识是解题的关键.
17. 如图,已知线段,垂足为a.
(1)求作四边形,使得点B,D分别在射线上,且,,;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设P,Q分别为(1)中四边形的边的中点,求证:直线相交于同一点.
【答案】(1)作图见解析;(2)证明见解析
【解析】(1)根据,点B在射线上,过点A作;根据等边三角形性质,得,分别过点A、B,为半径画圆弧,交点即为点C;再根据等边三角形的性质作CD,即可得到答案;
(2)设直线与相交于点S、直线与相交于点,根据平行线和相似三角形的性质,得,从而得,即可完成证明.
【详解】(1)作图如下:
四边形是所求作的四边形;
(2)设直线与相交于点S,
∵,
∴,
∴
设直线与相交于点,
同理.
∵P,Q分别为的中点,
∴,
∴
∴,
∴,
∴,
∴,
∴点S与重合,即三条直线相交于同一点.
【点睛】本题考查了尺规作图、等边三角形、直角三角形、平行线、相似三角形等基础知识,解题的关键是熟练掌握推理能力、空间观念、化归与转化思想,从而完成求解.
18.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使△ADE∽△ACB.
【答案】见解析。
【解析】(1)作线段BC的垂直平分线交AB于点D,连接CD即可.
(2)作∠ADT=∠ACB,射线DT交AC于点E,点E即为所求.
解:(1)如图,点D即为所求.
(2)如图,点E即为所求.
19. 如图,四边形ABCD中,,,连接AC.
(1)求证:≌;
(2)尺规作图:过点C作AB的垂线,垂足为不要求写作法,保留作图痕迹;
(3)在(2)的条件下,已知四边形ABCD的面积为20,,求CE的长.
【答案】见解析。
【解析】由得,结合,,即可根据AAS证明≌;
以C为圆心,CB为半径作弧,交线段AB延长线于F,分别以B、F为圆心,大于的线段长为半径作弧,两弧交于G、H,连接GH,交AF于E,作直线CE,则CE即为AB的垂线;
由≌,四边形ABCD的面积为20,可得,即可列出,而,即得.
本题考查全等三角形的判定和性质,涉及尺规作图、三角形面积等知识,解题的关键是掌握过一点作已知直线的垂线的方法:即是作线段BF的垂直平分线.
证明:,
,
在和中,
,
≌;
解:过点C作AB的垂线,垂足为E,如图:
解:由知:≌,
四边形ABCD的面积为20,
,
,
,
.
20.如图,已知Rt△ABC中,∠C=90°.
(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).
①作∠BAC的角平分线AD,交BC于点D;
②作线段AD的垂直平分线EF与AB相交于点O;
③以点O为圆心,以OD长为半径画圆,交边AB于点M.
(2)在(1)的条件下,求证:BC是⊙O的切线;
(3)若AM=4BM,AC=10,求⊙O的半径.
【答案】见解析。
【解析】(1)①以A为圆心,以任意长度为半径画弧,与AC、AB相交,再以两个交点为圆心,以大于两点之间距离的一半为半径画弧相交于∠BAC内部一点,将点A与它连接并延长,与BC交于点D,则AD为∠BAC的平分线;
②分别以点A、点D为圆心,以大于AD长度为半径画圆,将两圆交点连接,则EF为AD的垂直平分线,EF与AB交于点O;
(2)根据线段垂直平分线及角平分线的性质推出角之间的关系,再根据平行线的判定得出OD∥AC,从而得出OD⊥BC即可;
(3)根据题意得到线段之间的关系:OM=2BM,BO=3BM,AB=5BM,再根据相似三角形的性质求解即可.
解:(1)如图所示,
①以A为圆心,以任意长度为半径画弧,与AC、AB相交,再以两个交点为圆心,以大于两点之间距离的一半为半径画弧相交于∠BAC内部一点,将点A与它连接并延长,与BC交于点D,则AD为∠BAC的平分线;
②分别以点A、点D为圆心,以大于AD长度为半径画圆,将两圆交点连接,则EF为AD的垂直平分线,EF与AB交于点O;
③如图,⊙O与AB交于点M;
(2)证明:∵EF是AD的垂直平分线,且点O在AD上,
∴OA=OD,
∴∠OAD=∠ODA,
∵AD是∠BAC的平分线,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵AC⊥BC,
∴OD⊥BC,
故BC是⊙O的切线.
(3)根据题意可知OM=OA=OD=AM,AM=4BM,
∴OM=2BM,BO=3BM,AB=5BM,
∴==,
由(2)可知Rt△BOD与Rt△BAC有公共角∠B,
∴Rt△BOD∽Rt△BAC,
∴=,即=,解得DO=6,
故⊙O的半径为6.
21. 已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
【答案】(1)作图见详解
(2)9.1
【解析】【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;
(2)利用割补法,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,这样将△ABC分成三个小三角形,这三个小三角形分别以△ABC的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.
【小问1详解】
解:如下图所示,O为所求作点,
【小问2详解】
解:如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,
∵内切圆的半径为1.3,
∴OD=OF=OE=1.3,
∵三角形ABC的周长为14,
∴AB+BC+AC=14,
则
故三角形ABC的面积为9.1.
【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.
1. 如图,已知直线AB和AB上的一点C,过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以为半径作弧,两弧交于点F;
第三步:作直线CF,直线CF即为所求.
下列关于的说法正确的是( )
A. ≥ B. ≤ C. D.
2.如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )
A.AN=NC B.AN=BN C.MN=BC D.BN平分∠ABC
3.如图,已知△ABC.
(1)以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N.
(2)分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BAC的内部相交于点P.
(3)作射线AP交BC于点D.
(4)分别以A,D为圆心,以大于AD的长为半径画弧,两弧相交于G,H两点.
(5)作直线GH,交AC,AB分别于点E,F.
依据以上作图,若AF=2,CE=3,BD=,则CD的长是( )
A. B.1 C. D.4
4.已知: AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3),则点A的坐标为( )
A.(,3) B.(3﹣,3) C.(﹣,3) D.(2﹣,3)
5.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,按下列步骤作图:
步骤1:以点A为圆心,小于AC的长为半径作弧分别交AC、AB于点D、E.
步骤2:分别以点D、E为圆心,大于DE的长为半径作弧,两弧交于点M.
步骤3:作射线AM交BC于点F.
则AF的长为( )
A.6 B.3 C.4 D.6
6.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20° B.30° C.40° D.50°
7.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
8.如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交AB、AC于点M、N;再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
9.如图,已知线段AB长为4.现按照以下步骤作图:
①分别以点A,B为圆心,大于AB长为半径画弧,两弧分别相交于点E,F;
②过E,F两点作直线,与线段AB相交于点O.
则AO的长为 .
10. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,分别以点C,E为圆心,大于的长为半径作弧,两弧交于点P,作射线BP交AD的延长线于点F,∠CBE=60°,BC=6,则BF的长为________
11. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心、BC的长为半径画弧交AD于点E,再分别以点C,E为圆心、大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为______.
12.在Rt△ABC中,∠C=90°,∠B=30°,适当长为半径画弧,分别交AC,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点P,则 .
13.如图,为半⊙O的直径,,是半圆上的三等分点,,与半⊙O相切于点,点为上一动点(不与点,重合),直线交于点,于点,延长交于点,则下列结论正确的是______________.(写出所有正确结论的序号)
①;②的长为;③;④;⑤为定值.
14.如图,已知直线l1∥l2,直线l3分别与l1、l2交于点A、B.请用尺规作图法,在线段AB上求作一点P,使点P到l1、l2的距离相等.(保留作图痕迹,不写作法)
15.已知:如图,ABC为锐角三角形,AB=BC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP=.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC( )(填推理依据)
∴∠ABP=∠BAC
16.如图,在中,是边上一点,且.
(1)尺规作图(保留作图痕迹,不写作法)
①作的角平分线交于点;
②作线段的垂直平分线交于点.
(2)连接,直接写出线段和的数量关系及位置关系.
17. 如图,已知线段,垂足为a.
(1)求作四边形,使得点B,D分别在射线上,且,,;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设P,Q分别为(1)中四边形的边的中点,求证:直线相交于同一点.
18.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使△ADE∽△ACB.
19. 如图,四边形ABCD中,,,连接AC.
(1)求证:≌;
(2)尺规作图:过点C作AB的垂线,垂足为不要求写作法,保留作图痕迹;
(3)在(2)的条件下,已知四边形ABCD的面积为20,,求CE的长.
20.如图,已知Rt△ABC中,∠C=90°.
(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).
①作∠BAC的角平分线AD,交BC于点D;
②作线段AD的垂直平分线EF与AB相交于点O;
③以点O为圆心,以OD长为半径画圆,交边AB于点M.
(2)在(1)的条件下,求证:BC是⊙O的切线;
(3)若AM=4BM,AC=10,求⊙O的半径.
21. 已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
专题14 尺规作图问题大全(解析版)
1. 如图,已知直线AB和AB上的一点C,过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以为半径作弧,两弧交于点F;
第三步:作直线CF,直线CF即为所求.
下列关于的说法正确的是( )
A. ≥ B. ≤ C. D.
【答案】C
【解析】根据过直线外一点作已知直线的垂线的步骤,结合三角形三边关系判断即可.
由作图可知,分别以点和点为圆心,以为半径作弧,两弧交于点,此时.
【点睛】本题考查作图基本作图,解题的关键是理解题意,灵活运用所学知识解决问题.
2.如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )
A.AN=NC B.AN=BN C.MN=BC D.BN平分∠ABC
【答案】B
【解析】直接利用线段垂直平分线的性质求解.
由作法得DE垂直平分AB,
∴NA=NB.
3.如图,已知△ABC.
(1)以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N.
(2)分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BAC的内部相交于点P.
(3)作射线AP交BC于点D.
(4)分别以A,D为圆心,以大于AD的长为半径画弧,两弧相交于G,H两点.
(5)作直线GH,交AC,AB分别于点E,F.
依据以上作图,若AF=2,CE=3,BD=,则CD的长是( )
A. B.1 C. D.4
【答案】B
【解析】利用作法得AD平分∠BAC,EF垂直平分AD,所以∠EAD=∠FAD,EA=ED,FA=FD,再证明四边形AEDF为菱形得到AE=AF=2,然后利用平行线分线段成比例定理计算CD的长.
解:由作法得AD平分∠BAC,EF垂直平分AD,
∴∠EAD=∠FAD,EA=ED,FA=FD,
∵EA=ED,
∴∠EAD=∠EDA,
∴∠FAD=∠EDA,
∴DE∥AF,
同理可得AE∥DF,
∴四边形AEDF为平行四边形,
而EA=ED,
∴四边形AEDF为菱形,
∴AE=AF=2,
∵DE∥AB,
∴=,即=,
∴CD=.
4.已知: AOCD的顶点O(0,0),点C在x轴的正半轴上,按以下步骤作图:
①以点O为圆心,适当长为半径画弧,分别交OA于点M,交OC于点N.
②分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠AOC内相交于点E.
③画射线OE,交AD于点F(2,3),则点A的坐标为( )
A.(,3) B.(3﹣,3) C.(﹣,3) D.(2﹣,3)
【答案】A
【解析】利用基本作图得到∠AOF=∠COF,再根据平行四边形的性质得到AD∥OC,接着证明∠AOF=∠AFO得到OA=AF,设AF交y轴于M,如图,设A(t,3),则AM=﹣t,AO=AF=﹣t+2,利用勾股定理得到t2+32=(﹣t+2)2,然后解方程求出t即可得到A点坐标.
解:由作法得OE平分∠AOC,则∠AOF=∠COF,
∵四边形AOCD为平行四边形,
∴AD∥OC,
∴∠AFO=∠COF,
∴∠AOF=∠AFO,
∴OA=AF,
设AF交y轴于M,如图,
∵F(2,3),
∴MF=2,OM=3,
设A(t,3),
∴AM=﹣t,AO=AF=﹣t+2,
在Rt△OAM中,t2+32=(﹣t+2)2,解得t=﹣,
∴A(﹣,3).
故选:A.
5.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,按下列步骤作图:
步骤1:以点A为圆心,小于AC的长为半径作弧分别交AC、AB于点D、E.
步骤2:分别以点D、E为圆心,大于DE的长为半径作弧,两弧交于点M.
步骤3:作射线AM交BC于点F.
则AF的长为( )
A.6 B.3 C.4 D.6
【答案】B
【解析】利用基本作图得到AF平分∠BAC,过F点作FH⊥AB于H,如图,根据角平分线的性质得到FH=FC,再根据勾股定理计算出AC=6,设CF=x,则FH=x,然后利用面积法得到×10 x+×6 x=×6×8,解得x=3,最后利用勾股定理计算AF的长.
解:由作法得AF平分∠BAC,
过F点作FH⊥AB于H,如图,
∵AF平分∠BAC,FH⊥AB,FC⊥AC,
∴FH=FC,
在△ABC中,∵∠C=90°,AB=10,BC=8,
∴AC==6,
设CF=x,则FH=x,
∵S△ABF+S△ACF=S△ABC,
∴×10 x+×6 x=×6×8,解得x=3,
在Rt△ACF中,AF===3.
故选:B.
6.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20° B.30° C.40° D.50°
【答案】B
【解析】由作法得OD=OC,DO=DE,利用等腰三角形的性质和三角形内角和计算出∠OCD=∠ODC=70°,∠DEO=∠DOE=40°,然后利用三角形外角性质计算∠CDE的度数.
解:由作法得OD=OC,DO=DE,
∵OD=OC,
∴∠OCD=∠ODC=(180°﹣∠COD)=×(180°﹣40°)=70°,
∵DO=DE,
∴∠DEO=∠DOE=40°,
∵∠OCD=∠CDE+∠DEC,
∴∠CDE=70°﹣40°=30°.
7.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
【答案】A
【解析】利用基本作图得BD平分∠ABC,过D点作DE⊥AB于E,如图,根据角平分线的性质得到则DE=DC,再利用勾股定理计算出AC=8,然后利用面积法得到 DE×10+ CD×6=×6×8,最后解方程即可.
解:由作法得BD平分∠ABC,
过D点作DE⊥AB于E,如图,则DE=DC,
在Rt△ABC中,AC===8,
∵S△ABD+S△BCD=S△ABC,
∴ DE×10+ CD×6=×6×8,
即5CD+3CD=24,
∴CD=3.
故选:A.
8.如图,在△ABC中,以A为圆心,任意长为半径画弧,分别交AB、AC于点M、N;再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是( )
A.AD+BD<AB B.AD一定经过△ABC的重心
C.∠BAD=∠CAD D.AD一定经过△ABC的外心
【答案】C
【解析】根据题意判断AD是∠BAC的角平分线,可知C正确,根据重心和外心定义可知B、D选项错误,根据三角形任意两边之和大于第三边可知A错误.
由题可知AD是∠BAC的角平分线,
A、在△ABD中,AD+BD>AB,故选项A错误,不符合题意;
B、△ABC的重心是三条中线的交点,故选项B错误,不符合题意;
C、∵AD是∠BAC的角平分线,∴∠BAD=∠CAD,故选项C正确,符合题意;
D、△ABC的外心是三边中垂线的交点,故选项D错误,不符合题意.
9.如图,已知线段AB长为4.现按照以下步骤作图:
①分别以点A,B为圆心,大于AB长为半径画弧,两弧分别相交于点E,F;
②过E,F两点作直线,与线段AB相交于点O.
则AO的长为 .
【答案】2
【解析】直接利用基本作图方法得出EF垂直平分AB,即可得出答案.
由基本作图方法可得:EF垂直平分AB,
∵AB=4,
∴AO=AB=2.
10. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E,分别以点C,E为圆心,大于的长为半径作弧,两弧交于点P,作射线BP交AD的延长线于点F,∠CBE=60°,BC=6,则BF的长为________
【答案】
【解析】利用基本作图得到,平分,则,再根据平行四边形的性质和平行线的性质证明,所以,过点作于,如图,则,然后利用30°的三角函数值即可求出,从而得到的长.
【详解】由作法得,平分,
又∵∠CBE=60°,
,
四边形为平行四边形,
,
,
,
,
如图,过点作于,
∵,,
∴,
在中,,
,
.
故答案为:.
【点睛】本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的性质、等腰三角形的判定及性质以及解直角三角形的应用.
11. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心、BC的长为半径画弧交AD于点E,再分别以点C,E为圆心、大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为______.
【答案】
【解析】根据作图过程可得BF是∠EBC的平分线,然后证明△EBG≌△CBG,再利用勾股定理即可求出CG的长.
如图,连接EG,
根据作图过程可知:BF是∠EBC的平分线,
∴∠EBG=∠CBG,
在△EBG和△CBG中,
,
∴△EBG≌△CBG(SAS),
∴GE=GC,∠BEG=∠C=90°,
在Rt△ABE中,AB=6,BE=BC=10,
∴AE==8,
∴DE=AD﹣AE=10﹣8=2,
Rt△DGE中,DE=2,DG=DC﹣CG=6﹣CG,EG=CG,
∴EG2﹣DE2=DG2
∴CG2﹣22=(6﹣CG)2,
解得CG=.
故答案为:.
【点睛】本题考查了矩形的性质,作图-基本作图,解决本题的关键是掌握矩形的性质.
12.在Rt△ABC中,∠C=90°,∠B=30°,适当长为半径画弧,分别交AC,F;再分别以点E,F为圆心EF的长为半径画弧,两弧交于点P,则 .
【答案】BD=3CD.
【解析】证明AD=DB=2CD,可得结论.
∵∠C=90°,∠B=30°,
∴∠CAB=90°﹣30°=60°,
由作图可知AD平分∠CAB,
∴∠CAD=∠BAD=30°,
∴AD=2CD,
∵∠BAD=∠B=30°,
∴AD=DB,
∴BD=3CD,故答案为:BD=3CD.
13.如图,为半⊙O的直径,,是半圆上的三等分点,,与半⊙O相切于点,点为上一动点(不与点,重合),直线交于点,于点,延长交于点,则下列结论正确的是______________.(写出所有正确结论的序号)
①;②的长为;③;④;⑤为定值.
【答案】②⑤
【解析】①先根据圆的切线的性质可得,再根据半圆上的三等分点可得,然后根据圆周角定理可得,最后假设,根据角的和差、三角形的外角性质可得,这与点为上一动点相矛盾,由此即可得;
②根据弧长公式即可得;
③先根据等边三角形的性质可得,再根据角的和差即可得;
④先根据三角形的外角性质可得,从而可得对应角与不可能相等,由此即可得;⑤先根据相似三角形的判定与性质可得,从而可得,再根据等边三角形的性质可得,由此即可得.
【详解】如图,连接OP
与半⊙O相切于点
是半圆上的三等分点
是等边三角形
由圆周角定理得:
假设,则
又点为上一动点
不是一个定值,与相矛盾
即PB与PD不一定相等,结论①错误
则的长为,结论②正确
是等边三角形,
,则结论③错误
,即对应角与不可能相等
与不相似,则结论④错误
在和中,
,即
又是等边三角形,
即为定值,结论⑤正确
综上,结论正确的是②⑤
故答案为:②⑤.
【点睛】本题考查了圆周角定理、圆的切线的性质、弧长公式、相似三角形的判定与性质、等边三角形的判定与性质等知识点,较难的题①,先假设结论成立,再推出矛盾点是解题关键.
14.如图,已知直线l1∥l2,直线l3分别与l1、l2交于点A、B.请用尺规作图法,在线段AB上求作一点P,使点P到l1、l2的距离相等.(保留作图痕迹,不写作法)
【答案】见解析。
【解析】作线段AB的垂直平分线得到线段AB的中点,则中点为P点.
如图,点P为所作.
15.已知:如图,ABC为锐角三角形,AB=BC,CD∥AB.
求作:线段BP,使得点P在直线CD上,且∠ABP=.
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明.
证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC( )(填推理依据)
∴∠ABP=∠BAC
【答案】(1)见解析;(2)∠BPC,在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半
【解析】(1)按照作法的提示,逐步作图即可;
(2)利用平行线的性质证明: 再利用圆的性质得到:∠BPC=∠BAC,从而可得答案.
【详解】(1)依据作图提示作图如下:
(2)证明:∵CD∥AB,
∴∠ABP= .
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC=∠BAC(在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半. )(填推理依据)
∴∠ABP=∠BAC
故答案为:∠BPC;在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半.
【点睛】本题考查的是作图中复杂作图,同时考查了平行线的性质,圆的基本性质:在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半.掌握以上知识是解题的关键.
16.如图,在中,是边上一点,且.
(1)尺规作图(保留作图痕迹,不写作法)
①作的角平分线交于点;
②作线段的垂直平分线交于点.
(2)连接,直接写出线段和的数量关系及位置关系.
【答案】(1)①作图见解析,②作图见解析;(2)
【解析】(1)①根据角平分线的作图方法直接作图即可;②根据垂直平分线的作图方法直接作图即可;
(2)据等腰三角形的性质与垂直平分线的定义证明是的中位线,根据中位线的性质可得答案.
【详解】(1)如图,①即为所求作的的角平分线,
②过的垂线是所求作的线段的垂直平分线.
(2)如图,连接,
平分
由作图可知:
是的中位线,
【点睛】本题考查的是角平分线与垂直平分线的尺规作图,同时考查了三角形的中位线的性质,掌握以上知识是解题的关键.
17. 如图,已知线段,垂足为a.
(1)求作四边形,使得点B,D分别在射线上,且,,;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设P,Q分别为(1)中四边形的边的中点,求证:直线相交于同一点.
【答案】(1)作图见解析;(2)证明见解析
【解析】(1)根据,点B在射线上,过点A作;根据等边三角形性质,得,分别过点A、B,为半径画圆弧,交点即为点C;再根据等边三角形的性质作CD,即可得到答案;
(2)设直线与相交于点S、直线与相交于点,根据平行线和相似三角形的性质,得,从而得,即可完成证明.
【详解】(1)作图如下:
四边形是所求作的四边形;
(2)设直线与相交于点S,
∵,
∴,
∴
设直线与相交于点,
同理.
∵P,Q分别为的中点,
∴,
∴
∴,
∴,
∴,
∴,
∴点S与重合,即三条直线相交于同一点.
【点睛】本题考查了尺规作图、等边三角形、直角三角形、平行线、相似三角形等基础知识,解题的关键是熟练掌握推理能力、空间观念、化归与转化思想,从而完成求解.
18.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知△ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使△ADE∽△ACB.
【答案】见解析。
【解析】(1)作线段BC的垂直平分线交AB于点D,连接CD即可.
(2)作∠ADT=∠ACB,射线DT交AC于点E,点E即为所求.
解:(1)如图,点D即为所求.
(2)如图,点E即为所求.
19. 如图,四边形ABCD中,,,连接AC.
(1)求证:≌;
(2)尺规作图:过点C作AB的垂线,垂足为不要求写作法,保留作图痕迹;
(3)在(2)的条件下,已知四边形ABCD的面积为20,,求CE的长.
【答案】见解析。
【解析】由得,结合,,即可根据AAS证明≌;
以C为圆心,CB为半径作弧,交线段AB延长线于F,分别以B、F为圆心,大于的线段长为半径作弧,两弧交于G、H,连接GH,交AF于E,作直线CE,则CE即为AB的垂线;
由≌,四边形ABCD的面积为20,可得,即可列出,而,即得.
本题考查全等三角形的判定和性质,涉及尺规作图、三角形面积等知识,解题的关键是掌握过一点作已知直线的垂线的方法:即是作线段BF的垂直平分线.
证明:,
,
在和中,
,
≌;
解:过点C作AB的垂线,垂足为E,如图:
解:由知:≌,
四边形ABCD的面积为20,
,
,
,
.
20.如图,已知Rt△ABC中,∠C=90°.
(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).
①作∠BAC的角平分线AD,交BC于点D;
②作线段AD的垂直平分线EF与AB相交于点O;
③以点O为圆心,以OD长为半径画圆,交边AB于点M.
(2)在(1)的条件下,求证:BC是⊙O的切线;
(3)若AM=4BM,AC=10,求⊙O的半径.
【答案】见解析。
【解析】(1)①以A为圆心,以任意长度为半径画弧,与AC、AB相交,再以两个交点为圆心,以大于两点之间距离的一半为半径画弧相交于∠BAC内部一点,将点A与它连接并延长,与BC交于点D,则AD为∠BAC的平分线;
②分别以点A、点D为圆心,以大于AD长度为半径画圆,将两圆交点连接,则EF为AD的垂直平分线,EF与AB交于点O;
(2)根据线段垂直平分线及角平分线的性质推出角之间的关系,再根据平行线的判定得出OD∥AC,从而得出OD⊥BC即可;
(3)根据题意得到线段之间的关系:OM=2BM,BO=3BM,AB=5BM,再根据相似三角形的性质求解即可.
解:(1)如图所示,
①以A为圆心,以任意长度为半径画弧,与AC、AB相交,再以两个交点为圆心,以大于两点之间距离的一半为半径画弧相交于∠BAC内部一点,将点A与它连接并延长,与BC交于点D,则AD为∠BAC的平分线;
②分别以点A、点D为圆心,以大于AD长度为半径画圆,将两圆交点连接,则EF为AD的垂直平分线,EF与AB交于点O;
③如图,⊙O与AB交于点M;
(2)证明:∵EF是AD的垂直平分线,且点O在AD上,
∴OA=OD,
∴∠OAD=∠ODA,
∵AD是∠BAC的平分线,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵AC⊥BC,
∴OD⊥BC,
故BC是⊙O的切线.
(3)根据题意可知OM=OA=OD=AM,AM=4BM,
∴OM=2BM,BO=3BM,AB=5BM,
∴==,
由(2)可知Rt△BOD与Rt△BAC有公共角∠B,
∴Rt△BOD∽Rt△BAC,
∴=,即=,解得DO=6,
故⊙O的半径为6.
21. 已知:.
(1)尺规作图:用直尺和圆规作出内切圆的圆心O;(只保留作图痕迹,不写作法和证明)
(2)如果的周长为14,内切圆的半径为1.3,求的面积.
【答案】(1)作图见详解
(2)9.1
【解析】【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;
(2)利用割补法,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,这样将△ABC分成三个小三角形,这三个小三角形分别以△ABC的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.
【小问1详解】
解:如下图所示,O为所求作点,
【小问2详解】
解:如图所示,连接OA,OB,OC,作OD⊥AB,OE⊥BC,OF⊥AC,
∵内切圆的半径为1.3,
∴OD=OF=OE=1.3,
∵三角形ABC的周长为14,
∴AB+BC+AC=14,
则
故三角形ABC的面积为9.1.
【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.
同课章节目录
