人教版四年级下册数学三角形的内角和(课件)(共20张PPT)
文档属性
| 名称 | 人教版四年级下册数学三角形的内角和(课件)(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 00:00:00 | ||
图片预览

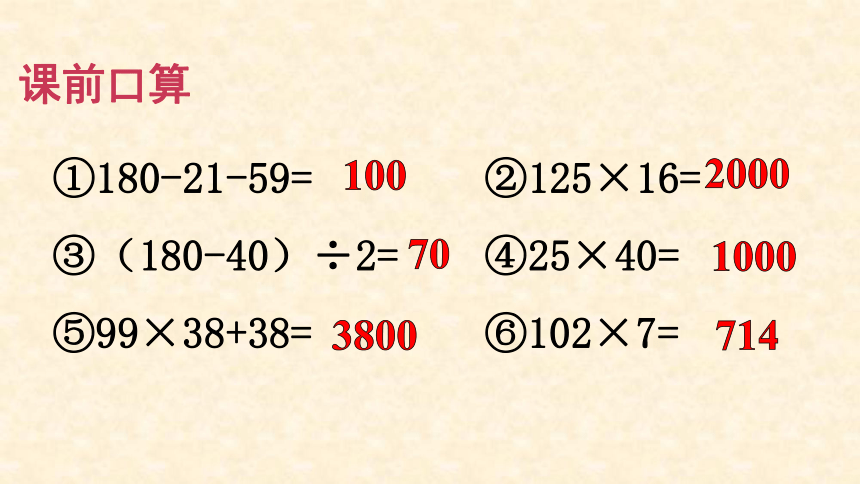




文档简介
(共20张PPT)
三角形的内角和
①180-21-59= ②125×16=
③(180-40)÷2= ④25×40=
⑤99×38+38= ⑥102×7=
100
70
3800
1000
714
2000
课前口算
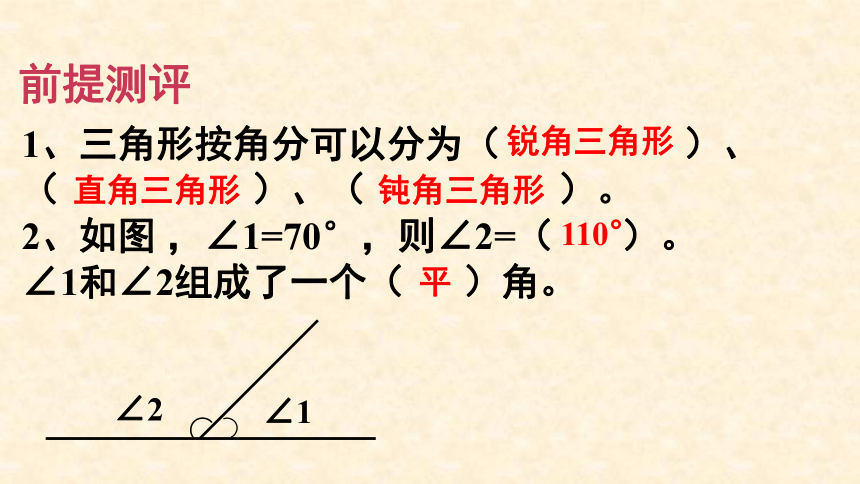
前提测评
1、三角形按角分可以分为( )、
( )、( )。
2、如图 ,∠1=70°,则∠2=( )。
∠1和∠2组成了一个( )角。
∠1
∠2
锐角三角形
钝角三角形
直角三角形
110°
平
前提测评
3、图中角的度数是( )度
40
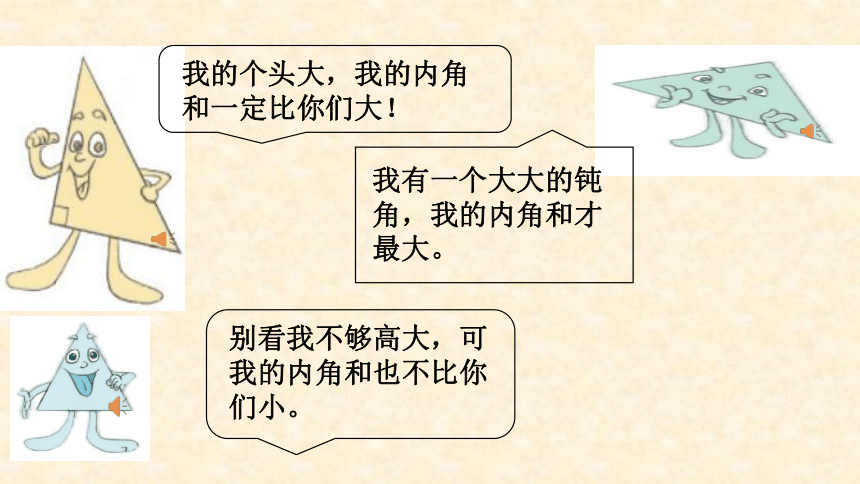
我的个头大,我的内角和一定比你们大!
我有一个大大的钝角,我的内角和才最大。
别看我不够高大,可我的内角和也不比你们小。
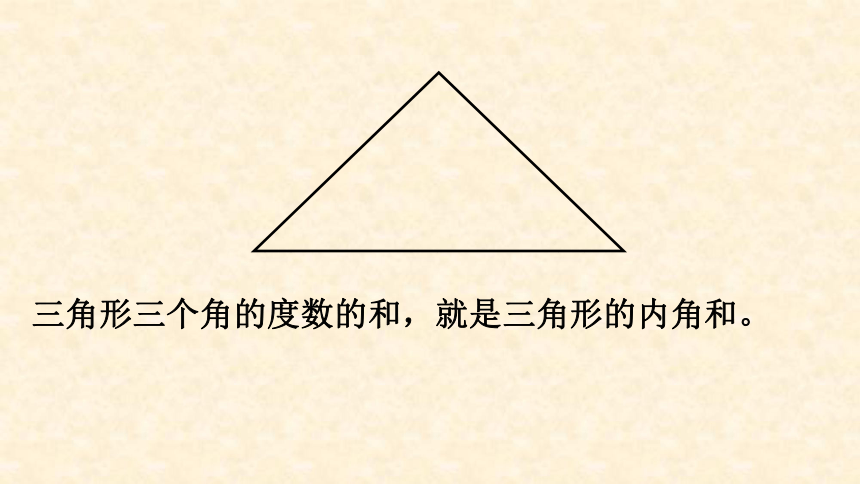
三角形的内角和
三角形三个角的度数的和,就是三角形的内角和。
量一量
1、给三角形的各个角标上∠1、∠2、∠3。
2、自己动手测量出∠1、∠2、∠3 的度数并填写在学习单上。
3、计算出三角形的3个内角的和 。
猜想
合作探究
1、前后四人为一组。
2、动手将三角形的三个角撕下来。
3、尝试将三角形的3个角拼成平角。
验证
剪拼法
1
3
2
2
3
1
拼成了一个平角。
折叠法
2
2
1
1
3
3
折成了一个平角。
归纳
锐角三角形的内角和是( ),直角三角形的内角和是( ),钝角三角形的内角和是( );而这三种三角形构成了任意三角形;因此,我们可以说( )三角形的内角和是( )。
180°
180°
180°
任意
180°
任意三角形的内角和是180度
目标检测一
我的个头大,我的内角和一定比你们大!
我有一个大大的钝角,我的内角和才最大。
别看我不够高大,可我的内角和也不比你们小。
1、算出下面各个未知角的度数。
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
目标检测二
2、求出三角形各个角的度数。
180°÷3=60°
(180°-96°)÷2
=42°
90°-40°=50°
3、爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
180°-(70°×2)=40°
答:它的顶角是40度。
一个三角形中最多有几个直角或钝角?为什么?
想一想
帕斯卡
帕斯卡:(1623—1662)
是法国著名的数学家、物理学家。早在300多年前,他12岁时,就独立发现了任何三角形的内角和都是180°
⌒
⌒
⌒
⌒
1
4
2
3
1
4
2
3
通过本节课的学习,你有什么收获?
猜想
验证
归纳
任意三角形的内角和是180度。
三角形的内角和
①180-21-59= ②125×16=
③(180-40)÷2= ④25×40=
⑤99×38+38= ⑥102×7=
100
70
3800
1000
714
2000
课前口算
前提测评
1、三角形按角分可以分为( )、
( )、( )。
2、如图 ,∠1=70°,则∠2=( )。
∠1和∠2组成了一个( )角。
∠1
∠2
锐角三角形
钝角三角形
直角三角形
110°
平
前提测评
3、图中角的度数是( )度
40
我的个头大,我的内角和一定比你们大!
我有一个大大的钝角,我的内角和才最大。
别看我不够高大,可我的内角和也不比你们小。
三角形的内角和
三角形三个角的度数的和,就是三角形的内角和。
量一量
1、给三角形的各个角标上∠1、∠2、∠3。
2、自己动手测量出∠1、∠2、∠3 的度数并填写在学习单上。
3、计算出三角形的3个内角的和 。
猜想
合作探究
1、前后四人为一组。
2、动手将三角形的三个角撕下来。
3、尝试将三角形的3个角拼成平角。
验证
剪拼法
1
3
2
2
3
1
拼成了一个平角。
折叠法
2
2
1
1
3
3
折成了一个平角。
归纳
锐角三角形的内角和是( ),直角三角形的内角和是( ),钝角三角形的内角和是( );而这三种三角形构成了任意三角形;因此,我们可以说( )三角形的内角和是( )。
180°
180°
180°
任意
180°
任意三角形的内角和是180度
目标检测一
我的个头大,我的内角和一定比你们大!
我有一个大大的钝角,我的内角和才最大。
别看我不够高大,可我的内角和也不比你们小。
1、算出下面各个未知角的度数。
180°-65°-37°
=78°
180°-90°-30°
=60°
180°-20°-25°
=135°
目标检测二
2、求出三角形各个角的度数。
180°÷3=60°
(180°-96°)÷2
=42°
90°-40°=50°
3、爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
180°-(70°×2)=40°
答:它的顶角是40度。
一个三角形中最多有几个直角或钝角?为什么?
想一想
帕斯卡
帕斯卡:(1623—1662)
是法国著名的数学家、物理学家。早在300多年前,他12岁时,就独立发现了任何三角形的内角和都是180°
⌒
⌒
⌒
⌒
1
4
2
3
1
4
2
3
通过本节课的学习,你有什么收获?
猜想
验证
归纳
任意三角形的内角和是180度。
