知识必备09 圆(3大模块知识清单 4种方法清单 16个考试清单真题专练)(含解析)
文档属性
| 名称 | 知识必备09 圆(3大模块知识清单 4种方法清单 16个考试清单真题专练)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 18:33:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
知识必备09 圆
方法1:圆中最值问题
一.选择题(共2小题)
1.(2023 江南区校级三模)如图,正方形的边长为5,以为圆心,2为半径作.点为上的动点,连接,并将绕点逆时针旋转得到,连接.在点运动的过程中,长度的最大值是
A. B. C. D.
2.(2023 明光市二模)如图,正方形的边长为2,点是射线上一个动点,点在上,且满足,则线段的最小值为( )
A. B.1 C. D.
二.填空题(共6小题)
3.(2023 南海区校级模拟)如图,点的坐标为,点的坐标为,点、点关于原点对称,点是平面上一点,且满足,则线段的最小值为 _______.
4.(2023 红旗区二模)如图,四边形中,,,,点是四边形内的一个动点,满足,连接、,则面积的最小值为 _______.
5.(2023 浙江模拟)在几何体表面上,蚂蚁怎样爬行路径最短?
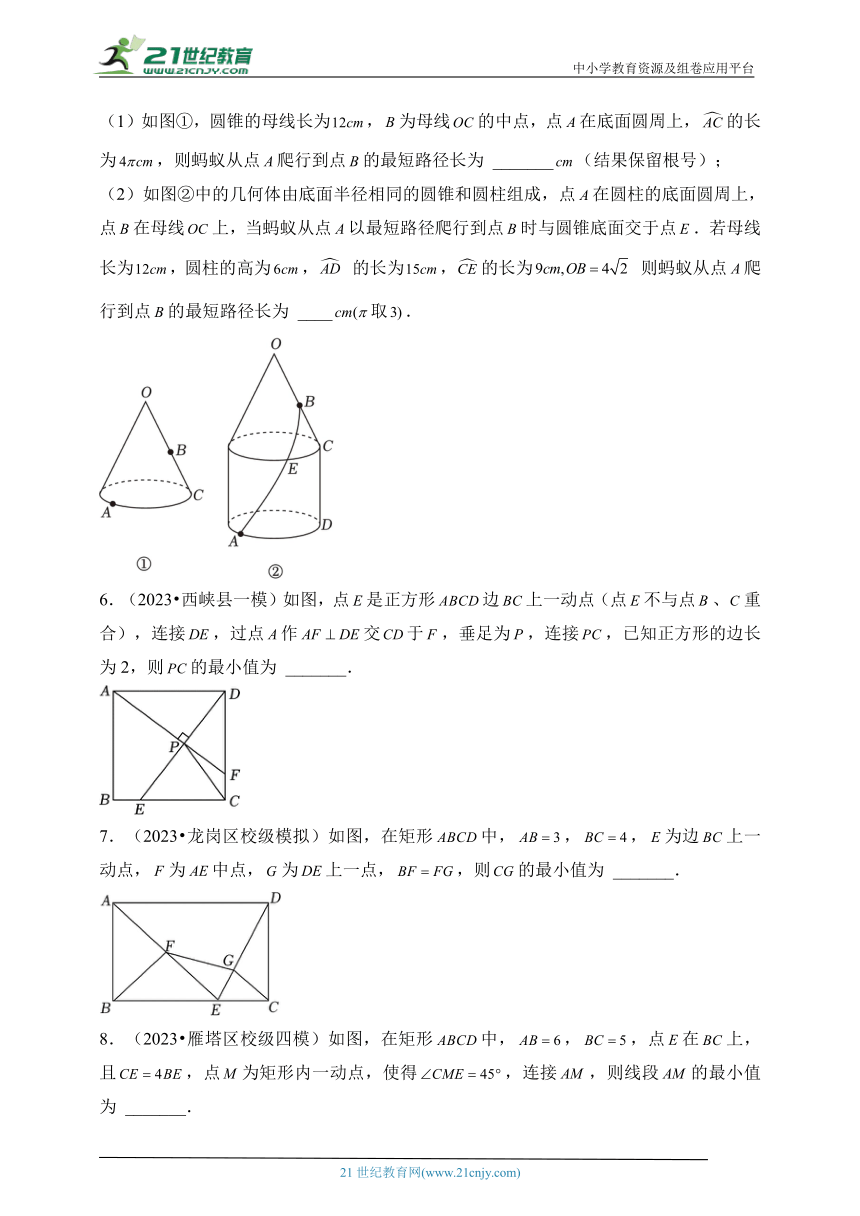
(1)如图①,圆锥的母线长为,为母线的中点,点在底面圆周上,的长为,则蚂蚁从点爬行到点的最短路径长为 _______(结果保留根号);
(2)如图②中的几何体由底面半径相同的圆锥和圆柱组成,点在圆柱的底面圆周上,点在母线上,当蚂蚁从点以最短路径爬行到点时与圆锥底面交于点.若母线长为,圆柱的高为, 的长为,的长为 则蚂蚁从点爬行到点的最短路径长为 ____取.
6.(2023 西峡县一模)如图,点是正方形边上一动点(点不与点、重合),连接,过点作交于,垂足为,连接,已知正方形的边长为2,则的最小值为 _______.
7.(2023 龙岗区校级模拟)如图,在矩形中,,,为边上一动点,为中点,为上一点,,则的最小值为 _______.
8.(2023 雁塔区校级四模)如图,在矩形中,,,点在上,且,点为矩形内一动点,使得,连接,则线段的最小值为 _______.
三.解答题(共4小题)
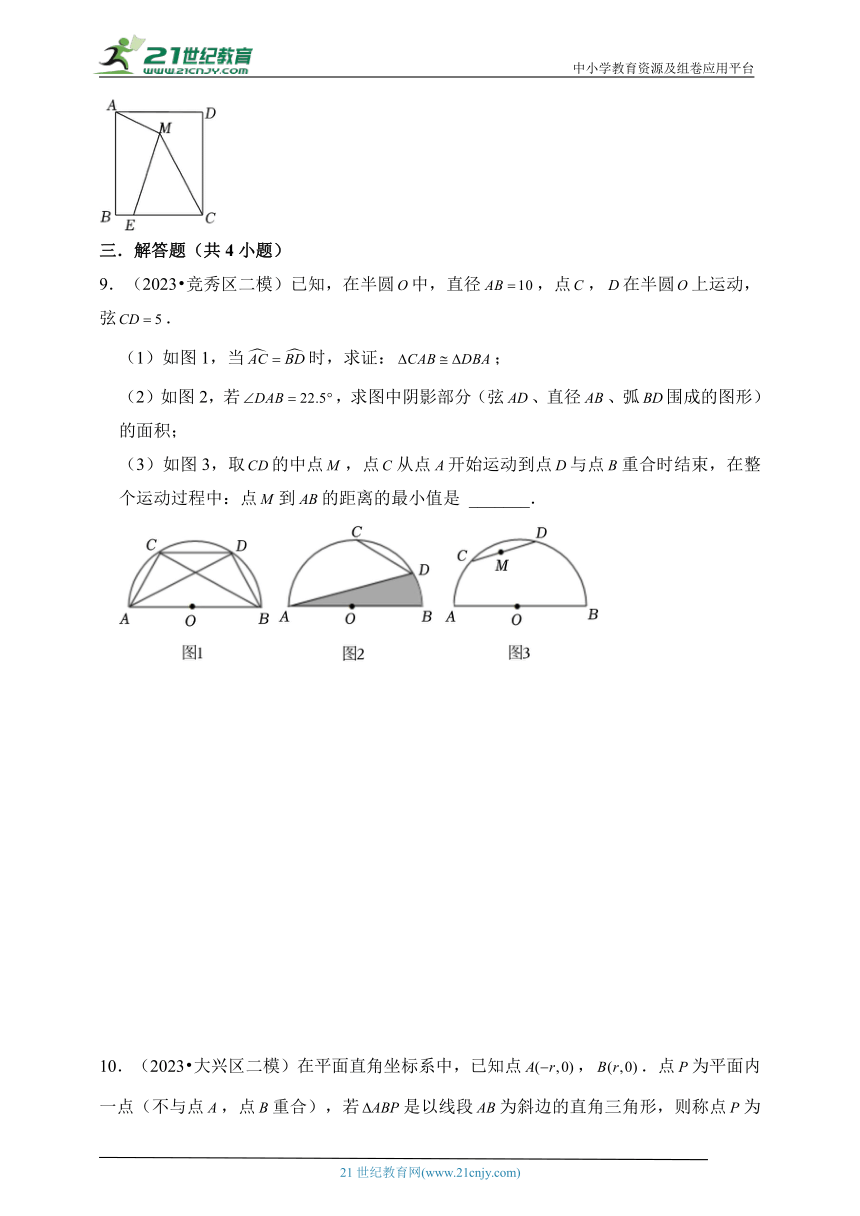
9.(2023 竞秀区二模)已知,在半圆中,直径,点,在半圆上运动,弦.
(1)如图1,当时,求证:;
(2)如图2,若,求图中阴影部分(弦、直径、弧围成的图形)的面积;
(3)如图3,取的中点,点从点开始运动到点与点重合时结束,在整个运动过程中:点到的距离的最小值是 _______.
10.(2023 大兴区二模)在平面直角坐标系中,已知点,.点为平面内一点(不与点,点重合),若是以线段为斜边的直角三角形,则称点为线段的直点.
(1)若,
①在点,,这三个点中,点 _______是线段的直点;
②点为线段的直点,点,求的取值范围;
(2)点在直线上,若点的横坐标 满足,点为线段的直点,且,直接写出的取值范围.
11.(2023 南海区一模)如图1,在矩形中,,,点在射线上运动,将沿翻折,使得点与点重合,连接交于点.
(1)【初步探究】当点落在边上时,求的长;
(2)【深入探究】在点的运动过程中,是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由;
(3)【拓展延伸】如图3,点为的中点,连接,点在射线上运动过程中,求长的最大值.
12.(2023 北京一模)在平面直角坐标系中,的半径为1,为上一点,点.
对于点给出如下定义:将点绕点顺时针旋转,得到点,点关于点的对称点为,称点为点的“对应点”.
(1)如图,已知点,点,点为点的“对应点”.
①在图中画出点;
②求证:;
(2)点在轴正半轴上,且,点为点的“对应点”,连接,当点在上运动时,直接写出长的最大值与最小值的积(用含的式子表示).
方法2:定点定长构造辅助圆
一.选择题(共1小题)
1.(2023 张家口一模)在中,要判断和的大小关系和均为锐角),同学们提供了许多方案,老师选取其中两位同学的方案(如图1和图2)
对于方案Ⅰ、Ⅱ说法正确的是
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行
C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
二.填空题(共1小题)
2.(2023 营口一模)如图,等边三角形和等边三角形,点,点分别为,的中点,,,绕点旋转过程中,的最大值为 _______.
三.解答题(共1小题)
3.(2023 新城区校级三模)圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.
(1)已知:如图1,,请利用圆规画出过、.三点的圆.若,则_______.
如图,中,,,.
(2)已知,如图2.点为边的中点,将沿方向平移2个单位长度,点、、的对应点分别为点、、,求四边形的面积和的大小.
(3)如图3,将边沿方向平移个单位至,是否存在这样的,使得直线上有一点,满足且此时四边形的面积最大?若存在,求出四边形面积的最大值及平移距离,若不存在,说明理由.
方法3:定弦定角构造辅助圆
一.选择题(共1小题)
1.(2023 肇东市校级模拟)如图,是的直径,,为的三等分点(更靠近点),点是上个动点,取弦的中点,则线段的最大值为
A.2 B. C. D.
二.填空题(共2小题)
2.(2023 利州区模拟)如图,正方形中,,动点从点出发向点运动,同时动点从点出发向点运动,点、运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段、相交于点,是线段上任意一点,则的最小值为 _______.
3.(2023 定远县校级一模)如图,半径为4的中,为直径,弦且过半径的中点,点为上一动点,于点.当点从点出发顺时针运动到点时,点所经过的路径长为 _______.
三.解答题(共2小题)
4.(2023 灞桥区校级模拟)问题提出:(1)如图①,为等腰三角形,,,是上一点,且平分的面积,则线段的长度为 _______.
问题探究:(2)如图②,中,,,试分析和判断的面积是否存在最大值,若存在,求出这个最大值;若不存在,请说明理由.
问题解决:(3)如图③,2023年第九届丝绸之路国际电影开幕式在西安曲江竞技中心举行,主办方要在会场旁规划一个四边形花圃,满足米,米,,,主办方打算过的中点点(入口)修建一条径直的通道(宽度忽略不计)其中点(出口)为四边形边上一点,通道把四边形分成面积相等并且尽可能大的两部分,分别规划成不同品种的花圃以供影迷休闲观赏.问是否存在满足上述条件的通道?若存在,请求出点距出口的距离的长;若不存在,请说明理由.
5.(2023 柯城区校级一模)如图,点与点的坐标分别是,,点是该直角坐标系内的一个动点.
(1)使的点有 ____个;
(2)若点在轴上,且,求满足条件的点的坐标;
(3)当点在轴上移动时,是否有最大值?若有,求点的坐标,并说明此时最大的理由;若没有,也请说明理由.
方法4:对角互补构造辅助圆
一.填空题(共1小题)
1.(2023 游仙区模拟)如图,在正方形中,,点是对角线上一点,连接,过点作,连接交于点,将沿翻折,得到.连接.交于点.若.则的面积是 _______.
二.解答题(共1小题)
2.(2023 朔城区一模)阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知内接于,点在上(不与点,,重合),过点分别作,,的垂线,垂足分别为点,,.求证:点,,在同一条直线上. 如下是他们的证明过程(不完整) 如图(1),连接,,,,取的中点,连接., 则,(依据 点,,,四点共圆, .(依据 又, . 同上可得点,,,四点共圆,
任务:
(1)填空:
①依据1指的是中点的定义及 __________________________;
②依据2指的是 ____.
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点是的中点时,,请你利用图(2)证明该结论的正确性.
一.垂径定理(共1小题)
1.(2023 宜昌)如图,,,都是的半径,,交于点.若,,则的长为
A.5 B.4 C.3 D.2
二.垂径定理的应用(共2小题)
2.(2023 永州)如图,是一个盛有水的容器的横截面,的半径为,水的最深处到水面的距离为,则水面的宽度为 _______.
3.(2023 广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为,拱高约为,则赵州桥主桥拱半径约为
A. B. C. D.
三.圆周角定理(共3小题)
4.(2023 广西)如图,点,,,在上,.则的度数是
A. B. C. D.
5.(2023 武汉)如图,,,都是的半径,.
(1)求证:;
(2)若,,求的半径.
6.(2023 齐齐哈尔)综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在和中,,,,连接,,延长交于点.则与的数量关系:_______,____;
(2)类比探究:如图2,在和中,,,,连接,,延长,交于点.请猜想与的数量关系及的度数,并说明理由;
(3)拓展延伸:如图3,和均为等腰直角三角形,,连接,,且点,,在一条直线上,过点作,垂足为点.则,,之间的数量关系:____;
(4)实践应用:正方形中,,若平面内存在点满足,,则____.
四.圆内接四边形的性质(共3小题)
7.(2023 西藏)如图,四边形内接于,为延长线上一点.若,则的度数是
A. B. C. D.
8.(2023 淮安)如图,四边形是的内接四边形,是的直径,,则的度数是 ____.
9.(2023 北京)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证平分,并求的大小;
(2)过点作交的延长线于点,若,,求此圆半径的长.
五.点与圆的位置关系(共1小题)
10.(2023 安徽)已知四边形内接于,对角线是的直径.
(1)如图1,连接,,若,求证:平分;
(2)如图2,为内一点,满足,.若,,求弦的长.
六.确定圆的条件(共1小题)
11.(2023 江西)如图,点,,,均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为
A.3个 B.4个 C.5个 D.6个
七.三角形的外接圆与外心(共2小题)
12.(2023 台湾)如图的方格纸中,每个方格的边长为1,、两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点、,使得的外心为,求的长度为何
A.4 B.5 C. D.
13.(2023 盘锦)如图,内接于,为的直径,延长到点,使得,连接.过点作,交于点,交于点,过点作,交的延长线于点.
(1)求证:与相切.
(2)若,,求的长.
八.直线与圆的位置关系(共1小题)
14.(2023 盐城)如图,在中,是上(异于点,的一点,恰好经过点,,于点,且平分.
(1)判断与的位置关系,并说明理由.
(2)若,,求的半径长.
九.切线的性质(共4小题)
15.(2023 青岛)如图,在平面直角坐标系中,已知点,,过原点,且与轴交于另一点,为的切线,为切点,是的直径,则的度数为 _______.
16.(2023 重庆)如图,是的切线,为切点,连接,.若,,,则的长度是
A.3 B. C. D.6
17.(2023 金华)如图,点在第一象限内,与轴相切于点,与轴相交于点,,连结,过点作于点.
(1)求证:四边形为矩形.
(2)已知的半径为4,,求弦的长.
18.(2023 南通)如图,等腰三角形的顶角,和底边相切于点,并与两腰,分别相交于,两点,连接,.
(1)求证:四边形是菱形;
(2)若的半径为2,求图中阴影部分的面积.
十.切线的判定(共2小题)
19.(2023 攀枝花)如图,为的直径,如果圆上的点恰使,求证:直线与相切.
20.(2023 江西)如图,在中,,,以为直径的与相交于点,为上一点,且.
(1)求的长;
(2)若,求证:为的切线.
十一.切线的判定与性质(共3小题)
21.(2023 鄂州)如图,为的直径,为上一点,点为的中点,过点作,交的延长线于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径长.
22.(2023 东营)如图,在中,,以为直径的交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
23.(2023 眉山)如图,中,以为直径的交于点,平分,过点作于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
十二.正多边形和圆(共3小题)
24.(2023 福建)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为,若用圆内接正十二边形作近似估计,可得的估计值为
A. B. C.3 D.
25.(2023 衡阳)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 _______.
26.(2023 上海)如果一个正多边形的中心角是,那么这个正多边形的边数为 _______.
十三.弧长的计算(共3小题)
27.(2023 青岛)如图,四边形是的内接四边形,,.若的半径为5,则的长为
A. B. C. D.
28.(2023 吉林)如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角,则的长为 _______.(结果保留
29.(2023 镇江)如图,扇形的半径为1,分别以点、为圆心,大于的长为半径画弧,两弧相交于点,,则的长_______(结果保留.
十四.扇形面积的计算(共1小题)
30.(2023 滨州)如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆,,相互经过彼此的圆心,则图中三个阴影部分的面积之和为
A. B. C. D.
十五.圆锥的计算(共3小题)
31.(2023 东营)如果圆锥侧面展开图的面积是,母线长是5,则这个圆锥的底面半径是
A.3 B.4 C.5 D.6
32.(2023 齐齐哈尔)若圆锥的底面半径长,母线长,则该圆锥的侧面积为 ___________.(结果保留
33.(2023 宿迁)若圆锥的底面半径为,侧面展开图是一个圆心角为的扇形,则这个圆锥的母线长是 _______.
十六.圆的综合题(共4小题)
34.(2023 枣庄)如图,为的直径,点是的中点,过点作射线的垂线,垂足为.
(1)求证:是的切线;
(2)若,,求的长;
(3)在(2)的条件下,求阴影部分的面积(用含有的式子表示).
35.(2023 兰州)如图,内接于,是的直径,,于点,交于点,交于点,,连接.
(1)求证:是的切线;
(2)判断的形状,并说明理由;
(3)当时,求的长.
36.(2023 杭州)如图,在中,直径垂直弦于点,连接,,,作于点,交线段于点(不与点,重合),连接.
(1)若,求的长.
(2)求证:.
(3)若,猜想的度数,并证明你的结论.
37.(2023 泰州)已知:、为圆上两定点,点在该圆上,为所对的圆周角.
知识回顾
(1)如图①,中,、位于直线异侧,.
①求的度数;
②若的半径为5,,求的长;
逆向思考
(2)如图②,若为圆内一点,且,,.求证:为该圆的圆心;
拓展应用
(3)如图③,在(2)的条件下,若,点在位于直线上方部分的圆弧上运动.点在上,满足的所有点中,必有一个点的位置始终不变.请证明.
知识必备09 圆
方法1:圆中最值问题
一.选择题(共2小题)
1.(2023 江南区校级三模)如图,正方形的边长为5,以为圆心,2为半径作.点为上的动点,连接,并将绕点逆时针旋转得到,连接.在点运动的过程中,长度的最大值是
A. B. C. D.
【分析】连接,,通过证明△可推出的轨迹是以为圆心,2为半径的圆上,从而求出取到最大值时的位置,结合勾股定理从而可求出的最大值.
【解答】解:连接,,
,
,
,,
△.
,
在以为圆心,2为半径的圆上,
连接,则当在的延长线上时,最长,
此时,
故选:.
【点评】本题主要考查了圆外一点到圆上一点的最大距离.本题的做题关键是通过全等来推出动点的轨迹.
2.(2023 明光市二模)如图,正方形的边长为2,点是射线上一个动点,点在上,且满足,则线段的最小值为( )
A. B.1 C. D.
【分析】根据已知证明,再证出,,说明点的运动轨迹是在以为直径的圆上,再根据点圆关系求出最值即可.
【解答】解:如图,连接,
,且,
,
,
,
,
,
,
,
点的运动轨迹是在以为直径的圆上,
如图,取中点,连接交于,则此时最小,
,
,
,
,
.
故选:.
【点评】本题考查了正方形的性质、相似三角形的性质等知识点的应用,点圆关系取最值的应用是解题关键.
二.填空题(共6小题)
3.(2023 南海区校级模拟)如图,点的坐标为,点的坐标为,点、点关于原点对称,点是平面上一点,且满足,则线段的最小值为 __3__.
【分析】根据直径所对的圆周角是直角,作出以为直径作,连接与交于点,此时的值最小,再根据点的坐标求出的长,即可得到答案.
【解答】解:如图,以为直径作,连接与交于点,过点作轴于点,
此时满足,的值最小,
点的坐标是,
,
点的坐标为,
,
,
.
故答案为:3.
【点评】本题主要考查了点和圆的位置关系,准确找到点的位置是解题的关键.掌握:直径所对的圆周角是直角.
4.(2023 红旗区二模)如图,四边形中,,,,点是四边形内的一个动点,满足,连接、,则面积的最小值为 ____.
【分析】取的中点.连接,过点作于点,过点作于点,交于点,则,根据垂线段最短可知,当,,三点共线时,的值最小,从而求得面积的最小值.
【解答】解:取的中点.连接,过点作于点,过点作于点,交于点,
则,
,,,
,
,
,
,
,
,
,
,
,
,
,
,,,
,
当,,三点共线时,的值最小,最小值为,
面积的最小值是:.
故答案为:.
【点评】本题考查了直径所对的圆周角是直角,垂线段最短,以及解直角三角形,解题的关键是学会用转化思想思考问题.
5.(2023 浙江模拟)在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为,为母线的中点,点在底面圆周上,的长为,则蚂蚁从点爬行到点的最短路径长为 ____(结果保留根号);
(2)如图②中的几何体由底面半径相同的圆锥和圆柱组成,点在圆柱的底面圆周上,点在母线上,当蚂蚁从点以最短路径爬行到点时与圆锥底面交于点.若母线长为,圆柱的高为, 的长为,的长为 则蚂蚁从点爬行到点的最短路径长为 ____取.
【分析】(1)先判断出为等边三角形,进而得出上等边三角形的高,即可得出结论;
(2)根据题意画出示意图,分别求出和的长,然后再求得长.
【解答】解:(1)如图③,将圆锥的侧面展开,连接,,.设.
的长为,
,,
,
,
是等边三角形,
,
,
.
最短的路径是线段,最短路径的长为.
故答案为:;
(2)将圆锥与圆柱的侧面展开蚂蚁从点爬行到点的最短路径的示意图如图④,最短路径为线段.
设与圆柱的展开图的上边的交点记作点,连接,并过点作,垂足为,
由题可知,,,
的长为,
展开后的线段.
母线长为,设,
,
,
,
作,垂足为,
,
,
,
,
,
,
,
.
故答案为:.
【点评】此题考查了平面展开最短路径问题,弧长公式,勾股定理,圆柱和圆锥的侧面展开图,等边三角形的判定和性质,作出辅助线构造出直角三角形是解本题的关键.
6.(2023 西峡县一模)如图,点是正方形边上一动点(点不与点、重合),连接,过点作交于,垂足为,连接,已知正方形的边长为2,则的最小值为 ____.
【分析】以为直径作,连接,交为点,根据点圆最值的性质,则为最小距离,再根据勾股定理计算即可.
【解答】解:,
点的运动轨迹是以为直径的圆上一段圆弧上,
如图,取中点,连接,交为点,则为所求,
正方形的边长为2,
,,
,
,
.
故答案为:.
【点评】本题考查了正方形的性质的应用,点圆最值的应用是解题关键.
7.(2023 龙岗区校级模拟)如图,在矩形中,,,为边上一动点,为中点,为上一点,,则的最小值为 ____.
【分析】如图1,连接,证明,则,根据圆周角定理可知:点在以为直径的圆上运动,取的中点,当,,三点共线时,的值最小,由此可解答.
【解答】解:如图1,连接,
四边形是矩形,
,,
是的中点,
,
,
,
,
点在以为直径的圆上运动,取的中点,连接,
当,,三点共线时,的值最小,如图2所示,
,
,
的最小值为.
故答案为:.
【点评】本题考查旋转的性质,矩形的性质,圆周角定理,线段的性质等知识,解题的关键是学会添加常用辅助线,构造动点的轨迹来解决问题,属于中考填空题中的压轴题.
8.(2023 雁塔区校级四模)如图,在矩形中,,,点在上,且,点为矩形内一动点,使得,连接,则线段的最小值为 ____.
【分析】作的外接圆,连接,当点是与的交点时,最小.
【解答】解:如图,作的外接圆,连接,,,作,,
,点在上,且,
,,
,
,
,,
,,
在中,,
当点是与的交点时,最小,
的最小值.
故答案为:.
【点评】本题考查了点圆位置关系求最值,解题的关键是构造辅助圆.
三.解答题(共4小题)
9.(2023 竞秀区二模)已知,在半圆中,直径,点,在半圆上运动,弦.
(1)如图1,当时,求证:;
(2)如图2,若,求图中阴影部分(弦、直径、弧围成的图形)的面积;
(3)如图3,取的中点,点从点开始运动到点与点重合时结束,在整个运动过程中:点到的距离的最小值是 ____.
【分析】(1)分别说明,,成立,用证明;
(2)将阴影面积分割:;
(3)先得到点在以为圆心,为半径的圆弧上运动,然后计算点从点开始运动时到的距离.
【解答】(1)证明:,
,
,
,,
,
,
又,
;
(2)解:过作于,连接,如图
半圆中,直径,
,
,
,
,,
,
;
(3)连接,,
是的中点,
,,
,
点在以为圆心,为半径的圆弧上运动,
过作,垂足为,
,
,
点到的距离的最小值是,
故答案为:.
【点评】本题考查了圆的性质、三角形全等的判定、与圆有关的面积计算、隐圆问题等知识点,对于(3),关键是确定点在以为圆心,为半径的圆弧上运动.
10.(2023 大兴区二模)在平面直角坐标系中,已知点,.点为平面内一点(不与点,点重合),若是以线段为斜边的直角三角形,则称点为线段的直点.
(1)若,
①在点,,这三个点中,点 ____是线段的直点;
②点为线段的直点,点,求的取值范围;
(2)点在直线上,若点的横坐标 满足,点为线段的直点,且,直接写出的取值范围.
【分析】(1)①按所给点,逐个计算,再根半径比较即可;
②连接作直线,交于、,则是的最小值,是的最大值,再分别计算、即可;
(2)若点在处和若点在处时,分别求出当时的长即可.
【解答】解:(1)①若,
则,.
以为圆心,1为半径作圆,
则线段的直点满足在上,
,,
,
在内,
不是线段的直点;
,
,
在上,
是线段的直点;
,
,
在外,
不是线段的直点;
故答案为:.
②如图,作直线,交于、,则是的最小值,是的最大值,
点,
,
,,
-1≤OP≤+1,
(2)在直线上且满足,
点在如图中的两个点之间,
当时,
若点在处,,
连接交于,
当时,,
即,
若点在处,,
连接交于,
当时,,
即,
的取值范围.
当时,
即,
的取值范围.
【点评】本题考查了点圆最值的应用解答,一次函数性质及勾股定理的计算是解题关键.
11.(2023 南海区一模)如图1,在矩形中,,,点在射线上运动,将沿翻折,使得点与点重合,连接交于点.
(1)【初步探究】当点落在边上时,求的长;
(2)【深入探究】在点的运动过程中,是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由;
(3)【拓展延伸】如图3,点为的中点,连接,点在射线上运动过程中,求长的最大值.
【分析】(1)由翻折得:,根据勾股定理可得,再由,即可求得答案;
(2)以为圆心,长为半径作,可得点在上运动,当点在线段上时,最小,此时,,由勾股定理可得,即可求得的最小值为;
(3)以为圆心,长为半径作,延长至,使,连接,根据三角形中位线定理可得,则最大时,最大,由于点在上运动,当经过点时,最大,即可求得答案.
【解答】解:(1)当点落在边上时,如图1,
四边形是矩形,
,,,
由翻折得:,
在中,,
;
(2)如图2,以为圆心,长为半径作,
由翻折得:,
点在上运动,
当点在线段上时,最小,此时,,
在中,,
,
故在点的运动过程中,存在最小值,的最小值为;
(3)如图3,以为圆心,长为半径作,延长至,使,连接,
,
点是的中点,
点为的中点,
是的中位线,
,
则最大时,最大,
由翻折得:,
点在上运动,
当经过点时,最大,如图4,
在中,,
,
,
故点在射线上运动过程中,长的最大值为.
【点评】此题是四边形综合题,主要考查了矩形的性质,翻折的性质,勾股定理,三角形的中位线定理,圆的有关性质,点到圆上各点距离的最大值和最小值的应用,解决问题的关键是运用三角形中位线定理和圆中的最值.
12.(2023 北京一模)在平面直角坐标系中,的半径为1,为上一点,点.
对于点给出如下定义:将点绕点顺时针旋转,得到点,点关于点的对称点为,称点为点的“对应点”.
(1)如图,已知点,点,点为点的“对应点”.
①在图中画出点;
②求证:;
(2)点在轴正半轴上,且,点为点的“对应点”,连接,当点在上运动时,直接写出长的最大值与最小值的积(用含的式子表示).
【分析】(1)①根据定义,先确定点的位置,再得出点的位置;
②过点作轴于点,利用证明△,设,利用中点坐标公式可求得,再运用两点间距离公式可求得,即可证得结论;
(2)点绕点顺时针旋转后得到点,可求得,则在以为圆心,为半径的圆上,设点关于点的对称点为,则,求得,则点在以为圆心为半径的圆上,再根据点到圆上各点距离的最大值和最小值即可求得答案.
【解答】(1)①解:如图,点即为所求;
②证明:过点作轴于点,
点,点,
,,
由旋转得:,,
,
,
,
,
△,
,,
,
,
设,又点,
点关于点的对称点为,
,,
解得:,,
,
由两点间距离公式可得:,
;
(2)解:点绕点顺时针旋转后得到点,
,,
设,当点在第四象限时,过点作轴于,过点作于,
则,,
,,
,
△,
,,
,
,
在上,
,
,
在以为圆心,为半径的圆上,
设点关于点的对称点为,则,
,,
点在以为圆心为半径的圆上,
的最大值为,的最小值为,
长的最大值与最小值的积为,
故答案为:.
【点评】本题考查圆的综合应用,熟练掌握三角形全等的判定及性质,两个相交圆的性质,图形旋转的性质,弄清定义,并能够判断出、点的运动轨迹是解题的关键.
方法2:定点定长构造辅助圆
一.选择题(共1小题)
1.(2023 张家口一模)在中,要判断和的大小关系和均为锐角),同学们提供了许多方案,老师选取其中两位同学的方案(如图1和图2)
对于方案Ⅰ、Ⅱ说法正确的是
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行
C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
【分析】根据作图得出,根等边对等角得出,根据即可判断方案Ⅰ;根据垂直平分线的性质可得,则,根据即可判断方案Ⅱ.
【解答】解:方案Ⅰ:
由作图可知:,
,
,
,
,
故方案Ⅰ可行,符合题意;
方案Ⅱ:
垂直平分,
,
,
,
,
故方案Ⅱ可行,符合题意;
故选:.
【点评】本题主要考查了等腰三角形的性质,垂直平分线的性质,三角形的外角定理,解题的关键是掌握等腰三角形等边对等角;垂直平分线上的点到两端距离相等.
二.填空题(共1小题)
2.(2023 营口一模)如图,等边三角形和等边三角形,点,点分别为,的中点,,,绕点旋转过程中,的最大值为 ____.
【分析】分析题意可知,点是在以为半径,点为圆心的圆上运动,连接,,以为半径,点为圆心作圆,反向延长与圆交于点,以此得到、、三点共线时,的值最大,再根据勾股定理分别算出、的值,则的最大值.
【解答】解:连接,,以为半径,点为圆心作圆,反向延长与圆交于点,如图,
绕点旋转,
点是在以为半径,点为圆心的圆上运动,
,
当点旋转到,即、、三点共线时,的值最大,最大为,
和都是等边三角形,
点,点分别为,的中点,,,
,,,,
在中,由勾股定理得,
在中,由勾股定理得,
根据旋转的性质得,,
,即的最大值为.
故答案为:.
【点评】本题主要考查等边三角形的性质、旋转的性质、勾股定理,解题关键在于确定点是在以为半径,点为圆心的圆上运动.
三.解答题(共1小题)
3.(2023 新城区校级三模)圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.
(1)已知:如图1,,请利用圆规画出过、.三点的圆.若,则____.
如图,中,,,.
(2)已知,如图2.点为边的中点,将沿方向平移2个单位长度,点、、的对应点分别为点、、,求四边形的面积和的大小.
(3)如图3,将边沿方向平移个单位至,是否存在这样的,使得直线上有一点,满足且此时四边形的面积最大?若存在,求出四边形面积的最大值及平移距离,若不存在,说明理由.
【分析】(1)利用圆的定义知,,三点共圆,再利用圆周角定理求解.
(2)根据图形的平移性质,判定平移后图形形状,继而确定面积的计算方式和方法,角度问题也迎刃而解.
(3)因角度不变,借助圆周角定点在圆周上运动时角度不变的思想,判断出点能够向右移动的最大距离,求出四边形的最大面积.
【解答】(1)以为圆心,为半径作辅助圆,如图,
,
,
,
故答案为.
(2)连接,,如图,
,
中,,,.
,,.
为斜边中点,
,
线段平移到之后,,,
四边形为菱形,
,
,
,且,
四边形为直角梯形,
,
(3)如图所示,以为斜边在的右侧作等腰直角三角形,以为圆心,为半径作,
当边沿方向平移个单位至时,
满足且此时四边形的面积最大,
直线与相切于点,
连接交于,过点作于,
则,,,
,,,
,,
,,,
,,
,
,
此时直角梯形的最大面积为:
.
【点评】本题主要考查图形的平移,圆心角,圆周角之间的关系,解题的关键是数形结合,找到极值点求解.
方法3:定弦定角构造辅助圆
一.选择题(共1小题)
1.(2023 肇东市校级模拟)如图,是的直径,,为的三等分点(更靠近点),点是上个动点,取弦的中点,则线段的最大值为
A.2 B. C. D.
【分析】如图,连接,,首先证明点的运动轨迹为以为直径的,连接,当点在的延长线上时,的值最大,利用勾股定理求出即可解决问题.
【解答】解:如图,连接,,
,
,
,
点的运动轨迹为以为直径的,连接,,
当点在的延长线上时,的值最大,
为的三等分点,
,
是等边三角形,
,
在中,,,,
,
,
,
的最大值为,
故选:.
【点评】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识,解题的关键是正确寻找点的运动轨迹,学会构造辅助圆解决问题.
二.填空题(共2小题)
2.(2023 利州区模拟)如图,正方形中,,动点从点出发向点运动,同时动点从点出发向点运动,点、运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段、相交于点,是线段上任意一点,则的最小值为 ____.
【分析】首先作出点关于的对称点从而可知当点、、在一条直线上时,路径最短,当点与点重合,点与点重合时,和均最短,即最短,然后由正方形的性质和轴对称图形的性质可知:,,最后由勾股定理即可求得的长,从而可求得的最小值.
【解答】解:如图作点关于的对称点,连接,
由轴对称的性质可知:,,
过点作垂直,垂足为,
易证,故可知的轨迹为以为直径的四分之一圆弧上,当点与点重合,点与点重合时,和均最短,
此时,最短.
四边形为正方形,
,.
.
在中,由勾股定理得:.
故答案为:.
【点评】本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点的位置是解题的关键.
3.(2023 定远县校级一模)如图,半径为4的中,为直径,弦且过半径的中点,点为上一动点,于点.当点从点出发顺时针运动到点时,点所经过的路径长为 ____.
【分析】由,得点在以为直径的圆上运动,当点与重合时,此时点与重合,当点与重合时,此时点与重合,则点从点出发顺时针运动到点时,点所经过的路径长为的长,然后根据条件求出所在圆的半径和圆心角,从而解决问题.
【解答】解:,
,
点在以为直径的圆上运动,
以为直径画半圆,连接,
当点与重合时,此时点与重合,
当点与重合时,此时点与重合,
点从点出发顺时针运动到点时,点所经过的路径长为的长,
点为的中点,
,
,
,,
,
,
,
所在圆的半径为,圆心角为,
的长为,
故答案为:.
【点评】本题主要考查了垂径定理,圆周角定理,定角对定弦,弧长公式等知识,确定点的运动路径是解题的关键.
三.解答题(共2小题)
4.(2023 灞桥区校级模拟)问题提出:(1)如图①,为等腰三角形,,,是上一点,且平分的面积,则线段的长度为 __4__.
问题探究:(2)如图②,中,,,试分析和判断的面积是否存在最大值,若存在,求出这个最大值;若不存在,请说明理由.
问题解决:(3)如图③,2023年第九届丝绸之路国际电影开幕式在西安曲江竞技中心举行,主办方要在会场旁规划一个四边形花圃,满足米,米,,,主办方打算过的中点点(入口)修建一条径直的通道(宽度忽略不计)其中点(出口)为四边形边上一点,通道把四边形分成面积相等并且尽可能大的两部分,分别规划成不同品种的花圃以供影迷休闲观赏.问是否存在满足上述条件的通道?若存在,请求出点距出口的距离的长;若不存在,请说明理由.
【分析】(1)由题意可知,是的中线,利用等腰三角形的性质推出,利用三角函数求解即可解决问题;
(2)当的边上的高最大时,三角形的面积最大,即过圆心,连接.求出的最大值即可得出答案;
(3)连接,.首先证明,求出,推出的面积是定值,要使得四边形的面积最大,只要的面积最大即可,因为为定值,为定角,推出当是等边三角形时,求出四边形的面积最大值,然后再求出,构建方程解决问题即可.
【解答】解:(1)如图①,
平分的面积,
,
,
,,
,
的长度为4,
故答案为:4;
(2)存在.如图②,
,都是定值,
点在上,并且当点在的中点时,的面积最大;
连接交于点,则,,
,
,,
,
答:的面积最大值是;
(3)存在.如图③,连接,,
是的中点,
,
,
又,
是等边三角形,
,,
,
,
米,
在中,米,为定值,
由(2)可知当时,即为等边三角形时的面积最大,
此时也为四边形的最大值的面积不变),
;
是等边三角形,
,
,
由,得:
,
解得:,
(米,
答:点距出口的距离的长为米.
【点评】本题是圆的综合题,考查了勾股定理,垂径定理,解直角三角形,等边三角形的判定和性质等知识,解题的关键是理解题意构造辅助圆,灵活运用所学知识解决问题,难度较大,属于中考压轴题.
5.(2023 柯城区校级一模)如图,点与点的坐标分别是,,点是该直角坐标系内的一个动点.
(1)使的点有 __无数__个;
(2)若点在轴上,且,求满足条件的点的坐标;
(3)当点在轴上移动时,是否有最大值?若有,求点的坐标,并说明此时最大的理由;若没有,也请说明理由.
【分析】(1)已知点、点是定点,要使,只需点在过点、点的圆上,且弧所对的圆心角为即可,显然符合条件的点有无数个.
(2)结合(1)中的分析可知:当点在轴的正半轴上时,点是(1)中的圆与轴的交点,借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点的坐标;当点在轴的负半轴上时,同理可求出符合条件的点的坐标.
(3)由三角形外角的性质可证得:在同圆或等圆中,同弧所对的圆周角大于同弧所对的圆外角.要最大,只需构造过点、点且与轴相切的圆,切点就是使得最大的点,然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题.
【解答】解:(1)以为边,在第一象限内作等边三角形,
以点为圆心,为半径作,交轴于点、.
在优弧上任取一点,如图1,
则.
使的点有无数个.
故答案为:无数.
(2)①当点在轴的正半轴上时,
过点作,垂足为,如图1.
点,点,
,.
.
点为圆心,,
.
.
是等边三角形,
.
.
点的坐标为,.
过点作轴,垂足为,连接,如图1,
点的坐标为,,
,.
、是与轴的交点,
.
,,
.
点为圆心,,
.
,.,.
②当点在轴的负半轴上时,
同理可得:..
综上所述:满足条件的点的坐标有:
,、,、、.
(3)当过点、的与轴相切于点时,最大.
理由:可证:,当最大时,最大.由 得:当最小即最小时,最大.所以当圆与轴相切时,最大.
①当点在轴的正半轴上时,
连接,作轴,垂足为,如图2.
与轴相切于点,
.
,,
.
四边形是矩形.
,.
.
,,,
.
②当点在轴的负半轴上时,
同理可得:.
理由:
①若点在轴的正半轴上,
在轴的正半轴上任取一点(不与点重合),
连接,,交于点,连接,如图2所示.
是的外角,
.
,
.
②若点在轴的负半轴上,
同理可证得:.
综上所述:当点在轴上移动时,有最大值,
此时点的坐标为和.
【点评】本题考查了垂径定理、圆周角定理、勾股定理、等边三角形的性质、矩形的判定与性质,切线的性质、三角形外角性质等知识,综合性强.同时也考查了创造性思维,有一定的难度.构造辅助圆是解决本题关键.
方法4:对角互补构造辅助圆
一.填空题(共1小题)
1.(2023 游仙区模拟)如图,在正方形中,,点是对角线上一点,连接,过点作,连接交于点,将沿翻折,得到.连接.交于点.若.则的面积是 ____.
【分析】如图,取的中点,连接,.连接交于.首先证明是等腰直角三角形求出,,解直角三角形求出,即可解决问题.
【解答】解:如图,取的中点,连接,.连接交于.
四边形是正方形,
,,,,
,
,
四边形对角互补,
,,,四点共圆,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
故答案为.
【点评】本题考查正方形的性质,翻折变换,解直角三角形,等腰三角形的判定和性质,四点共圆,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,学会利用辅助圆解决问题,属于中考填空题中的压轴题.
二.解答题(共1小题)
2.(2023 朔城区一模)阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知内接于,点在上(不与点,,重合),过点分别作,,的垂线,垂足分别为点,,.求证:点,,在同一条直线上. 如下是他们的证明过程(不完整) 如图(1),连接,,,,取的中点,连接., 则,(依据 点,,,四点共圆, .(依据 又, . 同上可得点,,,四点共圆,
任务:
(1)填空:
①依据1指的是中点的定义及 __直角三角形斜边上的中线等于斜边的一半__;
②依据2指的是 ____.
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点是的中点时,,请你利用图(2)证明该结论的正确性.
【分析】(1)利用直角直角三角形斜边上的中线的性质和圆内接四边形对角互补即可;
(2)利用直角三角形斜边上中线的性质证明点,,,和点,,,四点分别共圆,再说明,可证明结论;
(3)连接,,,利用证明,从而得出结论.
【解答】(1)解:①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半,
②依据2指的是圆内接四边形对角互补,
故答案为:①直角三角形斜边上的中线等于斜边的一半;②圆内接四边形对角互补;
(2)解:如图(1),连接,,,,取的中点,连接.,
则,
点,,,四点共圆,
,
又,
,
同上可得点,,,四点共圆,
,
,
,
点,,在同一直线上;
(3)证明:如图,连接,,,
点是的中点,
,
,,
又,,
,
,
.
【点评】本题主要考查了四点共圆,以及圆内接四边形的性质,角平分线的性质,全等三角形的判定与性质等知识,证明是解题的关键.
一.垂径定理(共1小题)
1.(2023 宜昌)如图,,,都是的半径,,交于点.若,,则的长为
A.5 B.4 C.3 D.2
【分析】根据垂径定理的推论得,再根据勾股定理得,即可求出答案.
【解答】解:,
,
在中,,
,
.
故选:.
【点评】本题考查了垂径定理和勾股定理,由垂径定理得是解题的关键.
二.垂径定理的应用(共2小题)
2.(2023 永州)如图,是一个盛有水的容器的横截面,的半径为,水的最深处到水面的距离为,则水面的宽度为 __16__.
【分析】过点作于点,交于点,连接,由垂径定理可得,然后在中根据勾股定理求出的长,即可得出的长.
【解答】解:如图,过点作于点,交于点,连接,
,
由题意知,,,
,
在中,,
,
故答案为:16.
【点评】本题考查了垂径定理,熟练掌握垂径定理:垂直于弦的直径平分这条弦,同时需熟练掌握勾股定理.
3.(2023 广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为,拱高约为,则赵州桥主桥拱半径约为
A. B. C. D.
【分析】设主桥拱半径,根据垂径定理得到,再利用勾股定理列方程求解,即可得到答案.
【解答】解:由题意可知,,,
设主桥拱半径为 ,
,
是半径,,
,
在中,,
,
解得.
故选:.
【点评】本题主要考查垂径定理的应用,涉及勾股定理,解题的关键是用勾股定理列出关于的方程解决问题.
三.圆周角定理(共3小题)
4.(2023 广西)如图,点,,,在上,.则的度数是
A. B. C. D.
【分析】由圆周角定理即可得到答案.
【解答】解:,,
.
故选:.
【点评】本题考查圆周角定理,关键是掌握圆周角定理.
5.(2023 武汉)如图,,,都是的半径,.
(1)求证:;
(2)若,,求的半径.
【分析】(1)利用圆周角定理可得,,结合可证明结论;
(2)过点作半径于点,可得,根据圆周角、弦、弧的关系可证得,即可求得,,利用勾股定理可求解,再利用勾股定理可求解圆的半径.
【解答】(1)证明:,,,
;
(2)解:过点作半径于点,连接,
,
,,
.
.
,,
,,
在 中,,
,
在中,,
,
解得,
即的半径是.
【点评】本题主要考查圆周角定理,勾股定理,垂径定理,圆心角、弦、弧的关系,掌握圆周角定理是解题的关键.
6.(2023 齐齐哈尔)综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在和中,,,,连接,,延长交于点.则与的数量关系:____,____;
(2)类比探究:如图2,在和中,,,,连接,,延长,交于点.请猜想与的数量关系及的度数,并说明理由;
(3)拓展延伸:如图3,和均为等腰直角三角形,,连接,,且点,,在一条直线上,过点作,垂足为点.则,,之间的数量关系:____;
(4)实践应用:正方形中,,若平面内存在点满足,,则____.
【分析】(1)根据等腰三角形的性质,利用证明即可得出结论;
(2)根据等腰三角形的性质,利用证明即可得出结论;
(3)根据等腰直角三角形的性质,利用证明即可得出结论;
(4)根据直径所对的圆周角是直角,先找到点,利用勾股定理计算出,再利用第3小题的结论得到三角形的高,的面积即可求出.
【解答】解:(1),,
理由如下:如图1所示:
和都是等腰三角形,
,,
又,
,
,
,
,
,
;
(2),,
理由如下:如图2所示:
证明:,
,
即,
又和都是等腰三角形,
,,
,
,
,,
,
;
(3),
理由如下:如图3所示:
和都是等腰三角形,
,,,
,
即:,
,
,
,,,
,
,
;
(4)如图4所示:
连接,以为直径作圆,
由题意,取满足条件的点,,则.,
,
,
连接,作于点,在上截取,
,,
,
,,
,
由(3)可得:,
,
,
同理可得:,
故的面积为:或.
【点评】本题是几何变换综合题,主要考查了全等三角形的判定,等腰三角形和等腰直角三角形的性质,圆周角定理,勾股定理,三角形的面积等知识,熟练掌握全等三角形的判定是解题的关键.
四.圆内接四边形的性质(共3小题)
7.(2023 西藏)如图,四边形内接于,为延长线上一点.若,则的度数是
A. B. C. D.
【分析】根据邻补角互补求出的度数,再根据圆内接四边形对角互补求出的度数,最后根据圆周角定理即可求出的度数.
【解答】解:,
,
四边形内接于,
,
,
,
故选:.
【点评】本题考查了圆内接四边形的性质、圆周角定理,熟练掌握这些定理和性质是解题的关键.
8.(2023 淮安)如图,四边形是的内接四边形,是的直径,,则的度数是 __120__.
【分析】连接,根据等边三角形的性质得到,再根据圆内接四边形的性质计算,得到答案.
【解答】解:如图,连接,
是的直径,,
,
为等边三角形,
,
四边形是的内接四边形,
,
,
故答案为:120.
【点评】本题考查的是圆内接四边形的性质、等边三角形的判定和性质,掌握圆内接四边形的对角互补是解题的关键.
9.(2023 北京)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证平分,并求的大小;
(2)过点作交的延长线于点,若,,求此圆半径的长.
【分析】(1)由圆周角定理得到,而,因此,得到平分,由圆内接四边形的性质得到,即可求出;
(2)由垂径定理推出是等边三角形,得到由,得到,由平行线的性质求出,由圆内接四边形的性质求出,得到,由直角三角形的性质得到,因为是圆的直径,即可得到圆半径的长是4.
【解答】(1)证明:,,
,
平分,
平分,
,
四边形是圆内接四边形,
,
,
,
,
;
(2)解:,,
,
,
,
是圆的直径,
垂直平分,
,
,
是等边三角形,
,
,
,
,
,
四边形是圆内接四边形,
,
,
,
,
,,
,
是圆的直径,
圆的半径长是4.
【点评】本题考查圆内接四边形的性质,圆周角定理,平行线的性质,等边三角形的判定和性质,关键是由圆内接四边形的性质得到,由垂径定理推出是等边三角形.
五.点与圆的位置关系(共1小题)
10.(2023 安徽)已知四边形内接于,对角线是的直径.
(1)如图1,连接,,若,求证:平分;
(2)如图2,为内一点,满足,.若,,求弦的长.
【分析】(1)由垂径定理证出,则可得出结论;
(2)延长交于,延长交于,证明四边形是平行四边形,则,根据勾股定理即可得出答案.
【解答】(1)证明:,
,
,
即平分;
(2)延长交于,延长交于,
,,
,
是的直径,
,
,,
,,
四边形是平行四边形,
,
.
【点评】本题主要考查了圆周角定理,垂径定理,勾股定理,平行四边形三角形的判定与性质,熟练掌握圆周角定理是解题的关键.
六.确定圆的条件(共1小题)
11.(2023 江西)如图,点,,,均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为
A.3个 B.4个 C.5个 D.6个
【分析】根据不在同一直线上的三点确定一个圆即可得到结论.
【解答】解:根据经过不在同一直线上的三点确定一个圆得,经过其中任意三个点,最多可画出圆的个数为6个,
故选:.
【点评】本题考查了确定圆的条件,熟练掌握不在同一直线上的三点确定一个圆是解题的关键.
七.三角形的外接圆与外心(共2小题)
12.(2023 台湾)如图的方格纸中,每个方格的边长为1,、两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点、,使得的外心为,求的长度为何
A.4 B.5 C. D.
【分析】三角形外心的性质:三角形的外心到三角形三顶点的距离相等,由此得到,从而确定、的位置.
【解答】解:的外心为,
,
,
,
、是方格纸格线的交点,
、的位置如图所示,
.
故选:.
【点评】本题考查三角形的外接圆与外心,勾股定理,关键是掌握三角形的外心的性质.
13.(2023 盘锦)如图,内接于,为的直径,延长到点,使得,连接.过点作,交于点,交于点,过点作,交的延长线于点.
(1)求证:与相切.
(2)若,,求的长.
【分析】(1)连接,先证为等腰直角三角形得,由得,,再根据圆心角与圆周角的关系得,然后可得,据此即可得出结论;
(2)先由勾股定理求出,则,再求出,然后根据得,由此可求出,进而可求出,最后再证四边形为平行四边形即可得出的长.
【解答】(1)证明:连接,如图:
为的直径,
,
,
为等腰直角三角形,
,
,
,,
,
,
,
即:,
又点在上,
为的半径,
为的切线,
即:与相切.
(2)解:由(1)可知:,,,
在中,,,
由勾股定理得:,
,
,,,
,
设,,
,
,
,
,
在中,,,
由勾股定理得:,
,,
四边形为平行四边形,
.
【点评】此题主要考查了切线的判定,平行四边形的判定和性质,勾股定理,圆周角定理等,熟练掌握切线的判定,平行四边形的判定和性质,理解直径所对的圆周角是直角,在同圆或等圆中,同弧(或等弧)所对的圆心角是圆周角度数的2倍是解答此题的关键,
八.直线与圆的位置关系(共1小题)
14.(2023 盐城)如图,在中,是上(异于点,的一点,恰好经过点,,于点,且平分.
(1)判断与的位置关系,并说明理由.
(2)若,,求的半径长.
【分析】(1)连接,证明,进而可以解决问题;
(2)利用勾股定理求出,然后根据平行线分线段成比例定理即可求出半径.
【解答】解:(1)与相切,理由如下:
如图,连接,
,
,
平分,
,
,
,
,
,
是的半径,
与相切;
(2),,,
,
,
,
,
,
,
的半径长为.
【点评】本题考查了直线和圆的位置关系,勾股定理,平行线分线段成比例定理,切线的判定,平行线的性质,解决本题的关键是掌握切线的判定方法.
九.切线的性质(共4小题)
15.(2023 青岛)如图,在平面直角坐标系中,已知点,,过原点,且与轴交于另一点,为的切线,为切点,是的直径,则的度数为 __60__.
【分析】先根据点,的坐标得,进而得的半径为1,然后再在中利用锐角三角函数求出,进而得,最后再证为等边三角形即可求出的度数.
【解答】解:点,,
,
过原点,
为的半径,
为的切线,
,,
在中,,,,
,
,
,
又,
三角形为等边三角形,
,
即的度数为.
故答案为:60.
【点评】此题主要考查了点的坐标,切线的性质,锐角三角函数,等边三角形的判定和性质等,熟练掌握切线的性质,锐角三角函数的定义和等边三角形的判定和性质是解答此题的关键.
16.(2023 重庆)如图,是的切线,为切点,连接,.若,,,则的长度是
A.3 B. C. D.6
【分析】根据切线的性质得到,求得,得到,根据勾股定理即可得到结论.
【解答】解:连接,
是的切线,
,
,
,,
,
,
,
故选:.
【点评】本题考查了切线的性质,解直角三角形,正确的作出辅助线是解题的关键.
17.(2023 金华)如图,点在第一象限内,与轴相切于点,与轴相交于点,,连结,过点作于点.
(1)求证:四边形为矩形.
(2)已知的半径为4,,求弦的长.
【分析】(1)根据切线的性质得到轴根据垂直的定义得到,根据矩形的判定定理得到四边形是矩形;
(2)连接,根据矩形的性质得到,根据勾股定理得到,根据垂径定理即可得到结论.
【解答】(1)证明:与轴相切于点,
轴
又,,
,
四边形是矩形;
(2)解:连接,
四边形是矩形,
,
,
,
,
.
【点评】本题考查了切线的性质,矩形的判定和性质,勾股定理,垂径定理,正确都作出辅助线是解题的关键.
18.(2023 南通)如图,等腰三角形的顶角,和底边相切于点,并与两腰,分别相交于,两点,连接,.
(1)求证:四边形是菱形;
(2)若的半径为2,求图中阴影部分的面积.
【分析】(1)连接,根据切线的性质可得,然后利用等腰三角形的三线合一性质可得,从而可得和都是等边三角形,最后利用等边三角形的性质可得,即可解答;
(2)连接交于点,利用菱形的性质可得,,,然后在中,利用勾股定理求出的长,从而求出的长,最后根据图中阴影部分的面积扇形的面积菱形的面积,进行计算即可解答.
【解答】(1)证明:连接,
和底边相切于点,
,
,,
,
,,
和都是等边三角形,
,,
,
四边形是菱形;
(2)解:连接交于点,
四边形是菱形,
,,,
在中,,
,
,
图中阴影部分的面积扇形的面积菱形的面积
,
图中阴影部分的面积为.
【点评】本题考查了切线的性质,扇形面积的计算,等腰三角形的性质,菱形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
十.切线的判定(共2小题)
19.(2023 攀枝花)如图,为的直径,如果圆上的点恰使,求证:直线与相切.
【分析】由等腰三角形的性质和圆周角定理得出,则,再由切线的判定即可得出结论.
【解答】证明:如图,连接,
,
,
为的直径,
,
,
,
,
即,
,
是的半径,
直线与相切.
【点评】本题考查了切线的判定、圆周角定理、直角三角形的性质、等腰三角形的性质等知识;熟练掌握圆周角定理和切线的判定是解题的关键.
20.(2023 江西)如图,在中,,,以为直径的与相交于点,为上一点,且.
(1)求的长;
(2)若,求证:为的切线.
【分析】(1)由圆周角定理求出,由邻补角的性质的,由弧长公式即可求出的长.
(2)由圆周角定理得到,因此,得到,因此,得到直径,即可证明为的切线.
【解答】(1)解:,
,
,
,
半径长是2,
的长;
(2)证明:,
,
,
,
,
直径,
为的切线.
【点评】本题考查弧长的计算,切线的判定,圆周角定理,关键是由圆周角定理求出,得到的度数,即可求出的长,求出的度数,得到的度数,即可求出,从而证明为的切线.
十一.切线的判定与性质(共3小题)
21.(2023 鄂州)如图,为的直径,为上一点,点为的中点,过点作,交的延长线于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径长.
【分析】(1)连接,由等弧所对的圆周角相等得出,根据同圆的半径相等得出,于是有,可得出,再根据,即可得出,从而问题得证;
(2)连接,,先根据切割线定理求出的长,然后由勾股定理求出、的长,再根据等弧所对的弦相等得出,在中根据勾股定理求出的长,即可求出的半径.
【解答】(1)证明:连接,
点为的中点,
,
,
,
,
,
,
,
,
,
,
即,
又为的半径,
是的切线;
(2)解:连接,,
由(1)知是的切线,
,
,,
,
在中,由勾股定理得,
在中,由勾股定理得,
点是的中点,
,
,
为的直径,
,
由勾股定理得,
的半径长是2.5.
【点评】本题考查了切线的判定与性质,圆周角定理的推论,勾股定理,弧、弦之间的关系定理,熟练掌握这些定理是解题的关键.
22.(2023 东营)如图,在中,,以为直径的交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
【分析】(1)连接,则,所以,由,得,则,所以,则,即可证明是的切线;
(2)连接,由是的直径,得,则,因为,,所以,可求得,再证明是等边三角形,则,而,根据弧长公式求出的长即可.
【解答】(1)证明:连接,则,
,
,
,
,
,
于点,
,
是的半径,,
是的切线.
(2)解:连接,
是的直径,
,
,
,,
,
,
,
,,
是等边三角形,
,
,
,
的长是.
【点评】此题重点考查等腰三角形的性质、平行线的判定与性质、切线的判定定理等知识,证明是解题的关键.
23.(2023 眉山)如图,中,以为直径的交于点,平分,过点作于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
【分析】(1)连接,证明,即可得到结论;
(2)根据锐角三角函数先求出半径和的长,然后证明,,进而根据线段的和差即可解决问题.
【解答】(1)证明:如图,连接,
平分,
,
,
,
,
,
,
,
是的半径,
是的切线;
(2)解:,,,
,
,
,
,
在中,,
,
为的直径,
,
平分,
,
,
,
,
,
的长为.
【点评】本题考查切线的判定和性质,全等三角形的判定和性质、等腰三角形的性质、圆周角定理、解题的关键是学会添加常用辅助线,构造基本图形解决问题.
十二.正多边形和圆(共3小题)
24.(2023 福建)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为,若用圆内接正十二边形作近似估计,可得的估计值为
A. B. C.3 D.
【分析】过作于,求得,根据直角三角形的性质得到,根据三角形的面积公式得到,于是得到正十二边形的面积为,根据圆的面积公式即可得到结论.
【解答】解:如图,是正十二边形的一条边,点是正十二边形的中心,
过作于,
在正十二边形中,,
,
,
正十二边形的面积为,
,
,
的近似值为3,
故选:.
【点评】本题考查了正多边形与圆,三角形的面积的计算,正确地作出辅助线是解题的关键.
25.(2023 衡阳)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 __10__.
【分析】先求出多边形的每一个内角为,可得到,即可求解.
【解答】解:多边形是正五边形,
正五边形的每一个内角为:,
,
正五边形的个数是.
故答案为:10.
【点评】本题主要考查正多边形与圆,多边形内角和问题,熟练掌握相关知识点是解题关键.
26.(2023 上海)如果一个正多边形的中心角是,那么这个正多边形的边数为 __18__.
【分析】根据正边形的中心角的度数为进行计算即可得到答案.
【解答】解:.
故这个正多边形的边数为18.
故答案为:18.
【点评】本题考查的是正多边形内角、外角和中心角的知识,掌握中心角的计算公式是解题的关键.
十三.弧长的计算(共3小题)
27.(2023 青岛)如图,四边形是的内接四边形,,.若的半径为5,则的长为
A. B. C. D.
【分析】根据圆周角的性质,计算出弧所对的圆心角度数,按照公式求出弧长即可.
【解答】解:连接、、,
,.
,,
,
.
故选:.
【点评】本题考查了弧长的计算和圆周角定理,同弧所对的圆周角是圆心角的一半.
28.(2023 吉林)如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角,则的长为 ____.(结果保留
【分析】由弧长公式:是弧长,是扇形圆心角的度数,是扇形的半径长),由此即可计算.
【解答】解:,半径为,
的长.
故答案为:.
【点评】本题考查弧长的计算,关键是掌握弧长公式.
29.(2023 镇江)如图,扇形的半径为1,分别以点、为圆心,大于的长为半径画弧,两弧相交于点,,则的长____(结果保留.
【分析】由等腰三角形的性质求出的度数,由弧长公式即可计算.
【解答】解:由作图知:垂直平分,
,
,
扇形的半径是1,
的长.
故答案为:.
【点评】本题考查弧长的计算,关键是掌握弧长公式.
十四.扇形面积的计算(共1小题)
30.(2023 滨州)如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆,,相互经过彼此的圆心,则图中三个阴影部分的面积之和为
A. B. C. D.
【分析】根据扇形面积的计算方法进行计算即可.
【解答】解:如图,连接,,,,,,,,,则△,△,△,△是边长为1的正三角形,
所以,
,
故选:.
【点评】本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的前提.
十五.圆锥的计算(共3小题)
31.(2023 东营)如果圆锥侧面展开图的面积是,母线长是5,则这个圆锥的底面半径是
A.3 B.4 C.5 D.6
【分析】根据圆锥的侧面积底面周长母线长即可求出答案.
【解答】解:设底面半径为,则底面周长,圆锥的侧面展开图的面积,
.
故选:.
【点评】本题考查了圆锥的计算,利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.
32.(2023 齐齐哈尔)若圆锥的底面半径长,母线长,则该圆锥的侧面积为 __6___.(结果保留
【分析】解析圆锥的侧面积底面周长母线长,把相应数值代入即可求解.
【解答】解:圆锥的侧面积
故答案为:.
【点评】本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.
33.(2023 宿迁)若圆锥的底面半径为,侧面展开图是一个圆心角为的扇形,则这个圆锥的母线长是 __6__.
【分析】设圆锥的母线长为,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,然后解关于的方程即可.
【解答】解:设圆锥的母线长为,
根据题意得,
解得,
即圆锥的母线长为.
故答案为6.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
十六.圆的综合题(共4小题)
34.(2023 枣庄)如图,为的直径,点是的中点,过点作射线的垂线,垂足为.
(1)求证:是的切线;
(2)若,,求的长;
(3)在(2)的条件下,求阴影部分的面积(用含有的式子表示).
【分析】(1)连接,证明,即可得到结论.
(2)连接,证明,从而可得,再代入求值即可.
(3)连接,,证明,从而可得,求出扇形的面积即可得到阴影部分的面积.
【解答】(1)证明:如图,连接,
点是的中点,
,
,
,
,
,
,
,
半径,
是的切线.
(2)解:如图,连接,
为的直径,
,
,
,
,
,
,
.
答:的长为.
(3)解:如图,连接、,
,
,
在中,,
,
,
,
,
,
是等边三角形,
,
,
,
,
.
答:阴影部分的面积为.
【点评】本题考查了圆的综合应用,熟练掌握切线的判断定理以及扇形面积的求法是解题的关键.
35.(2023 兰州)如图,内接于,是的直径,,于点,交于点,交于点,,连接.
(1)求证:是的切线;
(2)判断的形状,并说明理由;
(3)当时,求的长.
【分析】(1)连接,由圆周角定理得出,由等腰三角形的性质证出,由切线的判定可得出结论;
(2)由垂径定理得出,,证出,由直角三角形的性质得出,则可得出结论;
(3)由(2)可知,,,则可得出答案.
【解答】(1)证明:连接,
,
,
,
,
,
又,
,
又,
,
,
,
,
,
为半径,
是的切线;
(2)解:为等腰三角形,
理由:,
,,
,
,
,
,
又,
,
又,
,
,
,,
,
,
即为等腰三角形;
(3)解:由(2)可知,,,
,
,
.
【点评】本题是圆的综合题,考查了圆周角定理,切线的判定与性质,垂径定理,等腰三角形的判定与性质,直角三角形的性质,熟练掌握切线的判定是解题的关键.
36.(2023 杭州)如图,在中,直径垂直弦于点,连接,,,作于点,交线段于点(不与点,重合),连接.
(1)若,求的长.
(2)求证:.
(3)若,猜想的度数,并证明你的结论.
【分析】(1)由垂径定理可得,结合可得,根据圆周角定理可得,进而可得,通过证明,可得;
(2)证明,根据对应边成比例可得,再根据,,可证;
(3)方法一:设,,可证,,通过证明,进而可得,即,则.方法二:延长交于点,连接,证明是等腰直角三角形,即可解决问题.
【解答】(1)解:直径垂直弦,
,
,
,
,
,
由圆周角定理得,
,
在和中,
,
,
;
(2)证明:是的直径,
,
,
,
,
,
,
由(1)知,
,
,
;
(3)解:,证明如下:
解法一:如图,连接,
,
,
直径垂直弦,
,,
,
,
,
设,,
则,
,
,
,
,
,,,
,
,
,
,
,
在和中,
,
,
,
即,
,
.
解法二:
如图,延长交于点,连接,
,
,
,
,
是的直径,
,
,
,
,
,
,
是等腰直角三角形,
.
【点评】本题是圆的综合题,考查垂径定理,圆周角定理,全等三角形的判定与性质,相似三角形的判定与性质,等腰三角形的性质等,难度较大,解题的关键是综合应用上述知识点,特别是第3问,需要大胆猜想,再逐步论证.
37.(2023 泰州)已知:、为圆上两定点,点在该圆上,为所对的圆周角.
知识回顾
(1)如图①,中,、位于直线异侧,.
①求的度数;
②若的半径为5,,求的长;
逆向思考
(2)如图②,若为圆内一点,且,,.求证:为该圆的圆心;
拓展应用
(3)如图③,在(2)的条件下,若,点在位于直线上方部分的圆弧上运动.点在上,满足的所有点中,必有一个点的位置始终不变.请证明.
【分析】(1)①根据,结合圆周角定理求的度数;
②构造直角三角形;
(2)只要说明点到圆上、和另一点的距离相等即可;
(3)根据,构造一条线段等于,利用三角形全等来说明此线段和相等.
【解答】(1)解:①,,
,
.
②连接,过作,垂足为,
,,
是等腰直角三角形,且,
,,
是等腰直角三角形,
,
在直角三角形中,,
.
(2)延长交圆于点,则,
,
,
,
,
,
,
,
为该圆的圆心.
(3)过作的垂线交的延长线于点,连接,延长交圆于点,连接,,
,
,
是等腰直角三角形,
,
,,
,
是直径,
,
,
,
,
,
,
,
必有一个点的位置始终不变,点即为所求.
【点评】本题考查了圆周角定理,并对圆周角定理的逆命题进行了创新,还考查了解直角三角形和三角形全等的知识,对于(3)构造一条线段等于是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
知识必备09 圆
方法1:圆中最值问题
一.选择题(共2小题)
1.(2023 江南区校级三模)如图,正方形的边长为5,以为圆心,2为半径作.点为上的动点,连接,并将绕点逆时针旋转得到,连接.在点运动的过程中,长度的最大值是
A. B. C. D.
2.(2023 明光市二模)如图,正方形的边长为2,点是射线上一个动点,点在上,且满足,则线段的最小值为( )
A. B.1 C. D.
二.填空题(共6小题)
3.(2023 南海区校级模拟)如图,点的坐标为,点的坐标为,点、点关于原点对称,点是平面上一点,且满足,则线段的最小值为 _______.
4.(2023 红旗区二模)如图,四边形中,,,,点是四边形内的一个动点,满足,连接、,则面积的最小值为 _______.
5.(2023 浙江模拟)在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为,为母线的中点,点在底面圆周上,的长为,则蚂蚁从点爬行到点的最短路径长为 _______(结果保留根号);
(2)如图②中的几何体由底面半径相同的圆锥和圆柱组成,点在圆柱的底面圆周上,点在母线上,当蚂蚁从点以最短路径爬行到点时与圆锥底面交于点.若母线长为,圆柱的高为, 的长为,的长为 则蚂蚁从点爬行到点的最短路径长为 ____取.
6.(2023 西峡县一模)如图,点是正方形边上一动点(点不与点、重合),连接,过点作交于,垂足为,连接,已知正方形的边长为2,则的最小值为 _______.
7.(2023 龙岗区校级模拟)如图,在矩形中,,,为边上一动点,为中点,为上一点,,则的最小值为 _______.
8.(2023 雁塔区校级四模)如图,在矩形中,,,点在上,且,点为矩形内一动点,使得,连接,则线段的最小值为 _______.
三.解答题(共4小题)
9.(2023 竞秀区二模)已知,在半圆中,直径,点,在半圆上运动,弦.
(1)如图1,当时,求证:;
(2)如图2,若,求图中阴影部分(弦、直径、弧围成的图形)的面积;
(3)如图3,取的中点,点从点开始运动到点与点重合时结束,在整个运动过程中:点到的距离的最小值是 _______.
10.(2023 大兴区二模)在平面直角坐标系中,已知点,.点为平面内一点(不与点,点重合),若是以线段为斜边的直角三角形,则称点为线段的直点.
(1)若,
①在点,,这三个点中,点 _______是线段的直点;
②点为线段的直点,点,求的取值范围;
(2)点在直线上,若点的横坐标 满足,点为线段的直点,且,直接写出的取值范围.
11.(2023 南海区一模)如图1,在矩形中,,,点在射线上运动,将沿翻折,使得点与点重合,连接交于点.
(1)【初步探究】当点落在边上时,求的长;
(2)【深入探究】在点的运动过程中,是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由;
(3)【拓展延伸】如图3,点为的中点,连接,点在射线上运动过程中,求长的最大值.
12.(2023 北京一模)在平面直角坐标系中,的半径为1,为上一点,点.
对于点给出如下定义:将点绕点顺时针旋转,得到点,点关于点的对称点为,称点为点的“对应点”.
(1)如图,已知点,点,点为点的“对应点”.
①在图中画出点;
②求证:;
(2)点在轴正半轴上,且,点为点的“对应点”,连接,当点在上运动时,直接写出长的最大值与最小值的积(用含的式子表示).
方法2:定点定长构造辅助圆
一.选择题(共1小题)
1.(2023 张家口一模)在中,要判断和的大小关系和均为锐角),同学们提供了许多方案,老师选取其中两位同学的方案(如图1和图2)
对于方案Ⅰ、Ⅱ说法正确的是
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行
C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
二.填空题(共1小题)
2.(2023 营口一模)如图,等边三角形和等边三角形,点,点分别为,的中点,,,绕点旋转过程中,的最大值为 _______.
三.解答题(共1小题)
3.(2023 新城区校级三模)圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.
(1)已知:如图1,,请利用圆规画出过、.三点的圆.若,则_______.
如图,中,,,.
(2)已知,如图2.点为边的中点,将沿方向平移2个单位长度,点、、的对应点分别为点、、,求四边形的面积和的大小.
(3)如图3,将边沿方向平移个单位至,是否存在这样的,使得直线上有一点,满足且此时四边形的面积最大?若存在,求出四边形面积的最大值及平移距离,若不存在,说明理由.
方法3:定弦定角构造辅助圆
一.选择题(共1小题)
1.(2023 肇东市校级模拟)如图,是的直径,,为的三等分点(更靠近点),点是上个动点,取弦的中点,则线段的最大值为
A.2 B. C. D.
二.填空题(共2小题)
2.(2023 利州区模拟)如图,正方形中,,动点从点出发向点运动,同时动点从点出发向点运动,点、运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段、相交于点,是线段上任意一点,则的最小值为 _______.
3.(2023 定远县校级一模)如图,半径为4的中,为直径,弦且过半径的中点,点为上一动点,于点.当点从点出发顺时针运动到点时,点所经过的路径长为 _______.
三.解答题(共2小题)
4.(2023 灞桥区校级模拟)问题提出:(1)如图①,为等腰三角形,,,是上一点,且平分的面积,则线段的长度为 _______.
问题探究:(2)如图②,中,,,试分析和判断的面积是否存在最大值,若存在,求出这个最大值;若不存在,请说明理由.
问题解决:(3)如图③,2023年第九届丝绸之路国际电影开幕式在西安曲江竞技中心举行,主办方要在会场旁规划一个四边形花圃,满足米,米,,,主办方打算过的中点点(入口)修建一条径直的通道(宽度忽略不计)其中点(出口)为四边形边上一点,通道把四边形分成面积相等并且尽可能大的两部分,分别规划成不同品种的花圃以供影迷休闲观赏.问是否存在满足上述条件的通道?若存在,请求出点距出口的距离的长;若不存在,请说明理由.
5.(2023 柯城区校级一模)如图,点与点的坐标分别是,,点是该直角坐标系内的一个动点.
(1)使的点有 ____个;
(2)若点在轴上,且,求满足条件的点的坐标;
(3)当点在轴上移动时,是否有最大值?若有,求点的坐标,并说明此时最大的理由;若没有,也请说明理由.
方法4:对角互补构造辅助圆
一.填空题(共1小题)
1.(2023 游仙区模拟)如图,在正方形中,,点是对角线上一点,连接,过点作,连接交于点,将沿翻折,得到.连接.交于点.若.则的面积是 _______.
二.解答题(共1小题)
2.(2023 朔城区一模)阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知内接于,点在上(不与点,,重合),过点分别作,,的垂线,垂足分别为点,,.求证:点,,在同一条直线上. 如下是他们的证明过程(不完整) 如图(1),连接,,,,取的中点,连接., 则,(依据 点,,,四点共圆, .(依据 又, . 同上可得点,,,四点共圆,
任务:
(1)填空:
①依据1指的是中点的定义及 __________________________;
②依据2指的是 ____.
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点是的中点时,,请你利用图(2)证明该结论的正确性.
一.垂径定理(共1小题)
1.(2023 宜昌)如图,,,都是的半径,,交于点.若,,则的长为
A.5 B.4 C.3 D.2
二.垂径定理的应用(共2小题)
2.(2023 永州)如图,是一个盛有水的容器的横截面,的半径为,水的最深处到水面的距离为,则水面的宽度为 _______.
3.(2023 广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为,拱高约为,则赵州桥主桥拱半径约为
A. B. C. D.
三.圆周角定理(共3小题)
4.(2023 广西)如图,点,,,在上,.则的度数是
A. B. C. D.
5.(2023 武汉)如图,,,都是的半径,.
(1)求证:;
(2)若,,求的半径.
6.(2023 齐齐哈尔)综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在和中,,,,连接,,延长交于点.则与的数量关系:_______,____;
(2)类比探究:如图2,在和中,,,,连接,,延长,交于点.请猜想与的数量关系及的度数,并说明理由;
(3)拓展延伸:如图3,和均为等腰直角三角形,,连接,,且点,,在一条直线上,过点作,垂足为点.则,,之间的数量关系:____;
(4)实践应用:正方形中,,若平面内存在点满足,,则____.
四.圆内接四边形的性质(共3小题)
7.(2023 西藏)如图,四边形内接于,为延长线上一点.若,则的度数是
A. B. C. D.
8.(2023 淮安)如图,四边形是的内接四边形,是的直径,,则的度数是 ____.
9.(2023 北京)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证平分,并求的大小;
(2)过点作交的延长线于点,若,,求此圆半径的长.
五.点与圆的位置关系(共1小题)
10.(2023 安徽)已知四边形内接于,对角线是的直径.
(1)如图1,连接,,若,求证:平分;
(2)如图2,为内一点,满足,.若,,求弦的长.
六.确定圆的条件(共1小题)
11.(2023 江西)如图,点,,,均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为
A.3个 B.4个 C.5个 D.6个
七.三角形的外接圆与外心(共2小题)
12.(2023 台湾)如图的方格纸中,每个方格的边长为1,、两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点、,使得的外心为,求的长度为何
A.4 B.5 C. D.
13.(2023 盘锦)如图,内接于,为的直径,延长到点,使得,连接.过点作,交于点,交于点,过点作,交的延长线于点.
(1)求证:与相切.
(2)若,,求的长.
八.直线与圆的位置关系(共1小题)
14.(2023 盐城)如图,在中,是上(异于点,的一点,恰好经过点,,于点,且平分.
(1)判断与的位置关系,并说明理由.
(2)若,,求的半径长.
九.切线的性质(共4小题)
15.(2023 青岛)如图,在平面直角坐标系中,已知点,,过原点,且与轴交于另一点,为的切线,为切点,是的直径,则的度数为 _______.
16.(2023 重庆)如图,是的切线,为切点,连接,.若,,,则的长度是
A.3 B. C. D.6
17.(2023 金华)如图,点在第一象限内,与轴相切于点,与轴相交于点,,连结,过点作于点.
(1)求证:四边形为矩形.
(2)已知的半径为4,,求弦的长.
18.(2023 南通)如图,等腰三角形的顶角,和底边相切于点,并与两腰,分别相交于,两点,连接,.
(1)求证:四边形是菱形;
(2)若的半径为2,求图中阴影部分的面积.
十.切线的判定(共2小题)
19.(2023 攀枝花)如图,为的直径,如果圆上的点恰使,求证:直线与相切.
20.(2023 江西)如图,在中,,,以为直径的与相交于点,为上一点,且.
(1)求的长;
(2)若,求证:为的切线.
十一.切线的判定与性质(共3小题)
21.(2023 鄂州)如图,为的直径,为上一点,点为的中点,过点作,交的延长线于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径长.
22.(2023 东营)如图,在中,,以为直径的交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
23.(2023 眉山)如图,中,以为直径的交于点,平分,过点作于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
十二.正多边形和圆(共3小题)
24.(2023 福建)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为,若用圆内接正十二边形作近似估计,可得的估计值为
A. B. C.3 D.
25.(2023 衡阳)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 _______.
26.(2023 上海)如果一个正多边形的中心角是,那么这个正多边形的边数为 _______.
十三.弧长的计算(共3小题)
27.(2023 青岛)如图,四边形是的内接四边形,,.若的半径为5,则的长为
A. B. C. D.
28.(2023 吉林)如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角,则的长为 _______.(结果保留
29.(2023 镇江)如图,扇形的半径为1,分别以点、为圆心,大于的长为半径画弧,两弧相交于点,,则的长_______(结果保留.
十四.扇形面积的计算(共1小题)
30.(2023 滨州)如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆,,相互经过彼此的圆心,则图中三个阴影部分的面积之和为
A. B. C. D.
十五.圆锥的计算(共3小题)
31.(2023 东营)如果圆锥侧面展开图的面积是,母线长是5,则这个圆锥的底面半径是
A.3 B.4 C.5 D.6
32.(2023 齐齐哈尔)若圆锥的底面半径长,母线长,则该圆锥的侧面积为 ___________.(结果保留
33.(2023 宿迁)若圆锥的底面半径为,侧面展开图是一个圆心角为的扇形,则这个圆锥的母线长是 _______.
十六.圆的综合题(共4小题)
34.(2023 枣庄)如图,为的直径,点是的中点,过点作射线的垂线,垂足为.
(1)求证:是的切线;
(2)若,,求的长;
(3)在(2)的条件下,求阴影部分的面积(用含有的式子表示).
35.(2023 兰州)如图,内接于,是的直径,,于点,交于点,交于点,,连接.
(1)求证:是的切线;
(2)判断的形状,并说明理由;
(3)当时,求的长.
36.(2023 杭州)如图,在中,直径垂直弦于点,连接,,,作于点,交线段于点(不与点,重合),连接.
(1)若,求的长.
(2)求证:.
(3)若,猜想的度数,并证明你的结论.
37.(2023 泰州)已知:、为圆上两定点,点在该圆上,为所对的圆周角.
知识回顾
(1)如图①,中,、位于直线异侧,.
①求的度数;
②若的半径为5,,求的长;
逆向思考
(2)如图②,若为圆内一点,且,,.求证:为该圆的圆心;
拓展应用
(3)如图③,在(2)的条件下,若,点在位于直线上方部分的圆弧上运动.点在上,满足的所有点中,必有一个点的位置始终不变.请证明.
知识必备09 圆
方法1:圆中最值问题
一.选择题(共2小题)
1.(2023 江南区校级三模)如图,正方形的边长为5,以为圆心,2为半径作.点为上的动点,连接,并将绕点逆时针旋转得到,连接.在点运动的过程中,长度的最大值是
A. B. C. D.
【分析】连接,,通过证明△可推出的轨迹是以为圆心,2为半径的圆上,从而求出取到最大值时的位置,结合勾股定理从而可求出的最大值.
【解答】解:连接,,
,
,
,,
△.
,
在以为圆心,2为半径的圆上,
连接,则当在的延长线上时,最长,
此时,
故选:.
【点评】本题主要考查了圆外一点到圆上一点的最大距离.本题的做题关键是通过全等来推出动点的轨迹.
2.(2023 明光市二模)如图,正方形的边长为2,点是射线上一个动点,点在上,且满足,则线段的最小值为( )
A. B.1 C. D.
【分析】根据已知证明,再证出,,说明点的运动轨迹是在以为直径的圆上,再根据点圆关系求出最值即可.
【解答】解:如图,连接,
,且,
,
,
,
,
,
,
,
点的运动轨迹是在以为直径的圆上,
如图,取中点,连接交于,则此时最小,
,
,
,
,
.
故选:.
【点评】本题考查了正方形的性质、相似三角形的性质等知识点的应用,点圆关系取最值的应用是解题关键.
二.填空题(共6小题)
3.(2023 南海区校级模拟)如图,点的坐标为,点的坐标为,点、点关于原点对称,点是平面上一点,且满足,则线段的最小值为 __3__.
【分析】根据直径所对的圆周角是直角,作出以为直径作,连接与交于点,此时的值最小,再根据点的坐标求出的长,即可得到答案.
【解答】解:如图,以为直径作,连接与交于点,过点作轴于点,
此时满足,的值最小,
点的坐标是,
,
点的坐标为,
,
,
.
故答案为:3.
【点评】本题主要考查了点和圆的位置关系,准确找到点的位置是解题的关键.掌握:直径所对的圆周角是直角.
4.(2023 红旗区二模)如图,四边形中,,,,点是四边形内的一个动点,满足,连接、,则面积的最小值为 ____.
【分析】取的中点.连接,过点作于点,过点作于点,交于点,则,根据垂线段最短可知,当,,三点共线时,的值最小,从而求得面积的最小值.
【解答】解:取的中点.连接,过点作于点,过点作于点,交于点,
则,
,,,
,
,
,
,
,
,
,
,
,
,
,
,,,
,
当,,三点共线时,的值最小,最小值为,
面积的最小值是:.
故答案为:.
【点评】本题考查了直径所对的圆周角是直角,垂线段最短,以及解直角三角形,解题的关键是学会用转化思想思考问题.
5.(2023 浙江模拟)在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为,为母线的中点,点在底面圆周上,的长为,则蚂蚁从点爬行到点的最短路径长为 ____(结果保留根号);
(2)如图②中的几何体由底面半径相同的圆锥和圆柱组成,点在圆柱的底面圆周上,点在母线上,当蚂蚁从点以最短路径爬行到点时与圆锥底面交于点.若母线长为,圆柱的高为, 的长为,的长为 则蚂蚁从点爬行到点的最短路径长为 ____取.
【分析】(1)先判断出为等边三角形,进而得出上等边三角形的高,即可得出结论;
(2)根据题意画出示意图,分别求出和的长,然后再求得长.
【解答】解:(1)如图③,将圆锥的侧面展开,连接,,.设.
的长为,
,,
,
,
是等边三角形,
,
,
.
最短的路径是线段,最短路径的长为.
故答案为:;
(2)将圆锥与圆柱的侧面展开蚂蚁从点爬行到点的最短路径的示意图如图④,最短路径为线段.
设与圆柱的展开图的上边的交点记作点,连接,并过点作,垂足为,
由题可知,,,
的长为,
展开后的线段.
母线长为,设,
,
,
,
作,垂足为,
,
,
,
,
,
,
,
.
故答案为:.
【点评】此题考查了平面展开最短路径问题,弧长公式,勾股定理,圆柱和圆锥的侧面展开图,等边三角形的判定和性质,作出辅助线构造出直角三角形是解本题的关键.
6.(2023 西峡县一模)如图,点是正方形边上一动点(点不与点、重合),连接,过点作交于,垂足为,连接,已知正方形的边长为2,则的最小值为 ____.
【分析】以为直径作,连接,交为点,根据点圆最值的性质,则为最小距离,再根据勾股定理计算即可.
【解答】解:,
点的运动轨迹是以为直径的圆上一段圆弧上,
如图,取中点,连接,交为点,则为所求,
正方形的边长为2,
,,
,
,
.
故答案为:.
【点评】本题考查了正方形的性质的应用,点圆最值的应用是解题关键.
7.(2023 龙岗区校级模拟)如图,在矩形中,,,为边上一动点,为中点,为上一点,,则的最小值为 ____.
【分析】如图1,连接,证明,则,根据圆周角定理可知:点在以为直径的圆上运动,取的中点,当,,三点共线时,的值最小,由此可解答.
【解答】解:如图1,连接,
四边形是矩形,
,,
是的中点,
,
,
,
,
点在以为直径的圆上运动,取的中点,连接,
当,,三点共线时,的值最小,如图2所示,
,
,
的最小值为.
故答案为:.
【点评】本题考查旋转的性质,矩形的性质,圆周角定理,线段的性质等知识,解题的关键是学会添加常用辅助线,构造动点的轨迹来解决问题,属于中考填空题中的压轴题.
8.(2023 雁塔区校级四模)如图,在矩形中,,,点在上,且,点为矩形内一动点,使得,连接,则线段的最小值为 ____.
【分析】作的外接圆,连接,当点是与的交点时,最小.
【解答】解:如图,作的外接圆,连接,,,作,,
,点在上,且,
,,
,
,
,,
,,
在中,,
当点是与的交点时,最小,
的最小值.
故答案为:.
【点评】本题考查了点圆位置关系求最值,解题的关键是构造辅助圆.
三.解答题(共4小题)
9.(2023 竞秀区二模)已知,在半圆中,直径,点,在半圆上运动,弦.
(1)如图1,当时,求证:;
(2)如图2,若,求图中阴影部分(弦、直径、弧围成的图形)的面积;
(3)如图3,取的中点,点从点开始运动到点与点重合时结束,在整个运动过程中:点到的距离的最小值是 ____.
【分析】(1)分别说明,,成立,用证明;
(2)将阴影面积分割:;
(3)先得到点在以为圆心,为半径的圆弧上运动,然后计算点从点开始运动时到的距离.
【解答】(1)证明:,
,
,
,,
,
,
又,
;
(2)解:过作于,连接,如图
半圆中,直径,
,
,
,
,,
,
;
(3)连接,,
是的中点,
,,
,
点在以为圆心,为半径的圆弧上运动,
过作,垂足为,
,
,
点到的距离的最小值是,
故答案为:.
【点评】本题考查了圆的性质、三角形全等的判定、与圆有关的面积计算、隐圆问题等知识点,对于(3),关键是确定点在以为圆心,为半径的圆弧上运动.
10.(2023 大兴区二模)在平面直角坐标系中,已知点,.点为平面内一点(不与点,点重合),若是以线段为斜边的直角三角形,则称点为线段的直点.
(1)若,
①在点,,这三个点中,点 ____是线段的直点;
②点为线段的直点,点,求的取值范围;
(2)点在直线上,若点的横坐标 满足,点为线段的直点,且,直接写出的取值范围.
【分析】(1)①按所给点,逐个计算,再根半径比较即可;
②连接作直线,交于、,则是的最小值,是的最大值,再分别计算、即可;
(2)若点在处和若点在处时,分别求出当时的长即可.
【解答】解:(1)①若,
则,.
以为圆心,1为半径作圆,
则线段的直点满足在上,
,,
,
在内,
不是线段的直点;
,
,
在上,
是线段的直点;
,
,
在外,
不是线段的直点;
故答案为:.
②如图,作直线,交于、,则是的最小值,是的最大值,
点,
,
,,
-1≤OP≤+1,
(2)在直线上且满足,
点在如图中的两个点之间,
当时,
若点在处,,
连接交于,
当时,,
即,
若点在处,,
连接交于,
当时,,
即,
的取值范围.
当时,
即,
的取值范围.
【点评】本题考查了点圆最值的应用解答,一次函数性质及勾股定理的计算是解题关键.
11.(2023 南海区一模)如图1,在矩形中,,,点在射线上运动,将沿翻折,使得点与点重合,连接交于点.
(1)【初步探究】当点落在边上时,求的长;
(2)【深入探究】在点的运动过程中,是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由;
(3)【拓展延伸】如图3,点为的中点,连接,点在射线上运动过程中,求长的最大值.
【分析】(1)由翻折得:,根据勾股定理可得,再由,即可求得答案;
(2)以为圆心,长为半径作,可得点在上运动,当点在线段上时,最小,此时,,由勾股定理可得,即可求得的最小值为;
(3)以为圆心,长为半径作,延长至,使,连接,根据三角形中位线定理可得,则最大时,最大,由于点在上运动,当经过点时,最大,即可求得答案.
【解答】解:(1)当点落在边上时,如图1,
四边形是矩形,
,,,
由翻折得:,
在中,,
;
(2)如图2,以为圆心,长为半径作,
由翻折得:,
点在上运动,
当点在线段上时,最小,此时,,
在中,,
,
故在点的运动过程中,存在最小值,的最小值为;
(3)如图3,以为圆心,长为半径作,延长至,使,连接,
,
点是的中点,
点为的中点,
是的中位线,
,
则最大时,最大,
由翻折得:,
点在上运动,
当经过点时,最大,如图4,
在中,,
,
,
故点在射线上运动过程中,长的最大值为.
【点评】此题是四边形综合题,主要考查了矩形的性质,翻折的性质,勾股定理,三角形的中位线定理,圆的有关性质,点到圆上各点距离的最大值和最小值的应用,解决问题的关键是运用三角形中位线定理和圆中的最值.
12.(2023 北京一模)在平面直角坐标系中,的半径为1,为上一点,点.
对于点给出如下定义:将点绕点顺时针旋转,得到点,点关于点的对称点为,称点为点的“对应点”.
(1)如图,已知点,点,点为点的“对应点”.
①在图中画出点;
②求证:;
(2)点在轴正半轴上,且,点为点的“对应点”,连接,当点在上运动时,直接写出长的最大值与最小值的积(用含的式子表示).
【分析】(1)①根据定义,先确定点的位置,再得出点的位置;
②过点作轴于点,利用证明△,设,利用中点坐标公式可求得,再运用两点间距离公式可求得,即可证得结论;
(2)点绕点顺时针旋转后得到点,可求得,则在以为圆心,为半径的圆上,设点关于点的对称点为,则,求得,则点在以为圆心为半径的圆上,再根据点到圆上各点距离的最大值和最小值即可求得答案.
【解答】(1)①解:如图,点即为所求;
②证明:过点作轴于点,
点,点,
,,
由旋转得:,,
,
,
,
,
△,
,,
,
,
设,又点,
点关于点的对称点为,
,,
解得:,,
,
由两点间距离公式可得:,
;
(2)解:点绕点顺时针旋转后得到点,
,,
设,当点在第四象限时,过点作轴于,过点作于,
则,,
,,
,
△,
,,
,
,
在上,
,
,
在以为圆心,为半径的圆上,
设点关于点的对称点为,则,
,,
点在以为圆心为半径的圆上,
的最大值为,的最小值为,
长的最大值与最小值的积为,
故答案为:.
【点评】本题考查圆的综合应用,熟练掌握三角形全等的判定及性质,两个相交圆的性质,图形旋转的性质,弄清定义,并能够判断出、点的运动轨迹是解题的关键.
方法2:定点定长构造辅助圆
一.选择题(共1小题)
1.(2023 张家口一模)在中,要判断和的大小关系和均为锐角),同学们提供了许多方案,老师选取其中两位同学的方案(如图1和图2)
对于方案Ⅰ、Ⅱ说法正确的是
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行
C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
【分析】根据作图得出,根等边对等角得出,根据即可判断方案Ⅰ;根据垂直平分线的性质可得,则,根据即可判断方案Ⅱ.
【解答】解:方案Ⅰ:
由作图可知:,
,
,
,
,
故方案Ⅰ可行,符合题意;
方案Ⅱ:
垂直平分,
,
,
,
,
故方案Ⅱ可行,符合题意;
故选:.
【点评】本题主要考查了等腰三角形的性质,垂直平分线的性质,三角形的外角定理,解题的关键是掌握等腰三角形等边对等角;垂直平分线上的点到两端距离相等.
二.填空题(共1小题)
2.(2023 营口一模)如图,等边三角形和等边三角形,点,点分别为,的中点,,,绕点旋转过程中,的最大值为 ____.
【分析】分析题意可知,点是在以为半径,点为圆心的圆上运动,连接,,以为半径,点为圆心作圆,反向延长与圆交于点,以此得到、、三点共线时,的值最大,再根据勾股定理分别算出、的值,则的最大值.
【解答】解:连接,,以为半径,点为圆心作圆,反向延长与圆交于点,如图,
绕点旋转,
点是在以为半径,点为圆心的圆上运动,
,
当点旋转到,即、、三点共线时,的值最大,最大为,
和都是等边三角形,
点,点分别为,的中点,,,
,,,,
在中,由勾股定理得,
在中,由勾股定理得,
根据旋转的性质得,,
,即的最大值为.
故答案为:.
【点评】本题主要考查等边三角形的性质、旋转的性质、勾股定理,解题关键在于确定点是在以为半径,点为圆心的圆上运动.
三.解答题(共1小题)
3.(2023 新城区校级三模)圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.
(1)已知:如图1,,请利用圆规画出过、.三点的圆.若,则____.
如图,中,,,.
(2)已知,如图2.点为边的中点,将沿方向平移2个单位长度,点、、的对应点分别为点、、,求四边形的面积和的大小.
(3)如图3,将边沿方向平移个单位至,是否存在这样的,使得直线上有一点,满足且此时四边形的面积最大?若存在,求出四边形面积的最大值及平移距离,若不存在,说明理由.
【分析】(1)利用圆的定义知,,三点共圆,再利用圆周角定理求解.
(2)根据图形的平移性质,判定平移后图形形状,继而确定面积的计算方式和方法,角度问题也迎刃而解.
(3)因角度不变,借助圆周角定点在圆周上运动时角度不变的思想,判断出点能够向右移动的最大距离,求出四边形的最大面积.
【解答】(1)以为圆心,为半径作辅助圆,如图,
,
,
,
故答案为.
(2)连接,,如图,
,
中,,,.
,,.
为斜边中点,
,
线段平移到之后,,,
四边形为菱形,
,
,
,且,
四边形为直角梯形,
,
(3)如图所示,以为斜边在的右侧作等腰直角三角形,以为圆心,为半径作,
当边沿方向平移个单位至时,
满足且此时四边形的面积最大,
直线与相切于点,
连接交于,过点作于,
则,,,
,,,
,,
,,,
,,
,
,
此时直角梯形的最大面积为:
.
【点评】本题主要考查图形的平移,圆心角,圆周角之间的关系,解题的关键是数形结合,找到极值点求解.
方法3:定弦定角构造辅助圆
一.选择题(共1小题)
1.(2023 肇东市校级模拟)如图,是的直径,,为的三等分点(更靠近点),点是上个动点,取弦的中点,则线段的最大值为
A.2 B. C. D.
【分析】如图,连接,,首先证明点的运动轨迹为以为直径的,连接,当点在的延长线上时,的值最大,利用勾股定理求出即可解决问题.
【解答】解:如图,连接,,
,
,
,
点的运动轨迹为以为直径的,连接,,
当点在的延长线上时,的值最大,
为的三等分点,
,
是等边三角形,
,
在中,,,,
,
,
,
的最大值为,
故选:.
【点评】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识,解题的关键是正确寻找点的运动轨迹,学会构造辅助圆解决问题.
二.填空题(共2小题)
2.(2023 利州区模拟)如图,正方形中,,动点从点出发向点运动,同时动点从点出发向点运动,点、运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段、相交于点,是线段上任意一点,则的最小值为 ____.
【分析】首先作出点关于的对称点从而可知当点、、在一条直线上时,路径最短,当点与点重合,点与点重合时,和均最短,即最短,然后由正方形的性质和轴对称图形的性质可知:,,最后由勾股定理即可求得的长,从而可求得的最小值.
【解答】解:如图作点关于的对称点,连接,
由轴对称的性质可知:,,
过点作垂直,垂足为,
易证,故可知的轨迹为以为直径的四分之一圆弧上,当点与点重合,点与点重合时,和均最短,
此时,最短.
四边形为正方形,
,.
.
在中,由勾股定理得:.
故答案为:.
【点评】本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点的位置是解题的关键.
3.(2023 定远县校级一模)如图,半径为4的中,为直径,弦且过半径的中点,点为上一动点,于点.当点从点出发顺时针运动到点时,点所经过的路径长为 ____.
【分析】由,得点在以为直径的圆上运动,当点与重合时,此时点与重合,当点与重合时,此时点与重合,则点从点出发顺时针运动到点时,点所经过的路径长为的长,然后根据条件求出所在圆的半径和圆心角,从而解决问题.
【解答】解:,
,
点在以为直径的圆上运动,
以为直径画半圆,连接,
当点与重合时,此时点与重合,
当点与重合时,此时点与重合,
点从点出发顺时针运动到点时,点所经过的路径长为的长,
点为的中点,
,
,
,,
,
,
,
所在圆的半径为,圆心角为,
的长为,
故答案为:.
【点评】本题主要考查了垂径定理,圆周角定理,定角对定弦,弧长公式等知识,确定点的运动路径是解题的关键.
三.解答题(共2小题)
4.(2023 灞桥区校级模拟)问题提出:(1)如图①,为等腰三角形,,,是上一点,且平分的面积,则线段的长度为 __4__.
问题探究:(2)如图②,中,,,试分析和判断的面积是否存在最大值,若存在,求出这个最大值;若不存在,请说明理由.
问题解决:(3)如图③,2023年第九届丝绸之路国际电影开幕式在西安曲江竞技中心举行,主办方要在会场旁规划一个四边形花圃,满足米,米,,,主办方打算过的中点点(入口)修建一条径直的通道(宽度忽略不计)其中点(出口)为四边形边上一点,通道把四边形分成面积相等并且尽可能大的两部分,分别规划成不同品种的花圃以供影迷休闲观赏.问是否存在满足上述条件的通道?若存在,请求出点距出口的距离的长;若不存在,请说明理由.
【分析】(1)由题意可知,是的中线,利用等腰三角形的性质推出,利用三角函数求解即可解决问题;
(2)当的边上的高最大时,三角形的面积最大,即过圆心,连接.求出的最大值即可得出答案;
(3)连接,.首先证明,求出,推出的面积是定值,要使得四边形的面积最大,只要的面积最大即可,因为为定值,为定角,推出当是等边三角形时,求出四边形的面积最大值,然后再求出,构建方程解决问题即可.
【解答】解:(1)如图①,
平分的面积,
,
,
,,
,
的长度为4,
故答案为:4;
(2)存在.如图②,
,都是定值,
点在上,并且当点在的中点时,的面积最大;
连接交于点,则,,
,
,,
,
答:的面积最大值是;
(3)存在.如图③,连接,,
是的中点,
,
,
又,
是等边三角形,
,,
,
,
米,
在中,米,为定值,
由(2)可知当时,即为等边三角形时的面积最大,
此时也为四边形的最大值的面积不变),
;
是等边三角形,
,
,
由,得:
,
解得:,
(米,
答:点距出口的距离的长为米.
【点评】本题是圆的综合题,考查了勾股定理,垂径定理,解直角三角形,等边三角形的判定和性质等知识,解题的关键是理解题意构造辅助圆,灵活运用所学知识解决问题,难度较大,属于中考压轴题.
5.(2023 柯城区校级一模)如图,点与点的坐标分别是,,点是该直角坐标系内的一个动点.
(1)使的点有 __无数__个;
(2)若点在轴上,且,求满足条件的点的坐标;
(3)当点在轴上移动时,是否有最大值?若有,求点的坐标,并说明此时最大的理由;若没有,也请说明理由.
【分析】(1)已知点、点是定点,要使,只需点在过点、点的圆上,且弧所对的圆心角为即可,显然符合条件的点有无数个.
(2)结合(1)中的分析可知:当点在轴的正半轴上时,点是(1)中的圆与轴的交点,借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点的坐标;当点在轴的负半轴上时,同理可求出符合条件的点的坐标.
(3)由三角形外角的性质可证得:在同圆或等圆中,同弧所对的圆周角大于同弧所对的圆外角.要最大,只需构造过点、点且与轴相切的圆,切点就是使得最大的点,然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题.
【解答】解:(1)以为边,在第一象限内作等边三角形,
以点为圆心,为半径作,交轴于点、.
在优弧上任取一点,如图1,
则.
使的点有无数个.
故答案为:无数.
(2)①当点在轴的正半轴上时,
过点作,垂足为,如图1.
点,点,
,.
.
点为圆心,,
.
.
是等边三角形,
.
.
点的坐标为,.
过点作轴,垂足为,连接,如图1,
点的坐标为,,
,.
、是与轴的交点,
.
,,
.
点为圆心,,
.
,.,.
②当点在轴的负半轴上时,
同理可得:..
综上所述:满足条件的点的坐标有:
,、,、、.
(3)当过点、的与轴相切于点时,最大.
理由:可证:,当最大时,最大.由 得:当最小即最小时,最大.所以当圆与轴相切时,最大.
①当点在轴的正半轴上时,
连接,作轴,垂足为,如图2.
与轴相切于点,
.
,,
.
四边形是矩形.
,.
.
,,,
.
②当点在轴的负半轴上时,
同理可得:.
理由:
①若点在轴的正半轴上,
在轴的正半轴上任取一点(不与点重合),
连接,,交于点,连接,如图2所示.
是的外角,
.
,
.
②若点在轴的负半轴上,
同理可证得:.
综上所述:当点在轴上移动时,有最大值,
此时点的坐标为和.
【点评】本题考查了垂径定理、圆周角定理、勾股定理、等边三角形的性质、矩形的判定与性质,切线的性质、三角形外角性质等知识,综合性强.同时也考查了创造性思维,有一定的难度.构造辅助圆是解决本题关键.
方法4:对角互补构造辅助圆
一.填空题(共1小题)
1.(2023 游仙区模拟)如图,在正方形中,,点是对角线上一点,连接,过点作,连接交于点,将沿翻折,得到.连接.交于点.若.则的面积是 ____.
【分析】如图,取的中点,连接,.连接交于.首先证明是等腰直角三角形求出,,解直角三角形求出,即可解决问题.
【解答】解:如图,取的中点,连接,.连接交于.
四边形是正方形,
,,,,
,
,
四边形对角互补,
,,,四点共圆,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
故答案为.
【点评】本题考查正方形的性质,翻折变换,解直角三角形,等腰三角形的判定和性质,四点共圆,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,学会利用辅助圆解决问题,属于中考填空题中的压轴题.
二.解答题(共1小题)
2.(2023 朔城区一模)阅读下列材料,并完成相应的任务.
西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线). 某数学兴趣小组的同学们尝试证明该定理. 如图(1),已知内接于,点在上(不与点,,重合),过点分别作,,的垂线,垂足分别为点,,.求证:点,,在同一条直线上. 如下是他们的证明过程(不完整) 如图(1),连接,,,,取的中点,连接., 则,(依据 点,,,四点共圆, .(依据 又, . 同上可得点,,,四点共圆,
任务:
(1)填空:
①依据1指的是中点的定义及 __直角三角形斜边上的中线等于斜边的一半__;
②依据2指的是 ____.
(2)请将证明过程补充完整.
(3)善于思考的小虎发现当点是的中点时,,请你利用图(2)证明该结论的正确性.
【分析】(1)利用直角直角三角形斜边上的中线的性质和圆内接四边形对角互补即可;
(2)利用直角三角形斜边上中线的性质证明点,,,和点,,,四点分别共圆,再说明,可证明结论;
(3)连接,,,利用证明,从而得出结论.
【解答】(1)解:①依据1指的是中点的定义及直角三角形斜边上的中线等于斜边的一半,
②依据2指的是圆内接四边形对角互补,
故答案为:①直角三角形斜边上的中线等于斜边的一半;②圆内接四边形对角互补;
(2)解:如图(1),连接,,,,取的中点,连接.,
则,
点,,,四点共圆,
,
又,
,
同上可得点,,,四点共圆,
,
,
,
点,,在同一直线上;
(3)证明:如图,连接,,,
点是的中点,
,
,,
又,,
,
,
.
【点评】本题主要考查了四点共圆,以及圆内接四边形的性质,角平分线的性质,全等三角形的判定与性质等知识,证明是解题的关键.
一.垂径定理(共1小题)
1.(2023 宜昌)如图,,,都是的半径,,交于点.若,,则的长为
A.5 B.4 C.3 D.2
【分析】根据垂径定理的推论得,再根据勾股定理得,即可求出答案.
【解答】解:,
,
在中,,
,
.
故选:.
【点评】本题考查了垂径定理和勾股定理,由垂径定理得是解题的关键.
二.垂径定理的应用(共2小题)
2.(2023 永州)如图,是一个盛有水的容器的横截面,的半径为,水的最深处到水面的距离为,则水面的宽度为 __16__.
【分析】过点作于点,交于点,连接,由垂径定理可得,然后在中根据勾股定理求出的长,即可得出的长.
【解答】解:如图,过点作于点,交于点,连接,
,
由题意知,,,
,
在中,,
,
故答案为:16.
【点评】本题考查了垂径定理,熟练掌握垂径定理:垂直于弦的直径平分这条弦,同时需熟练掌握勾股定理.
3.(2023 广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为,拱高约为,则赵州桥主桥拱半径约为
A. B. C. D.
【分析】设主桥拱半径,根据垂径定理得到,再利用勾股定理列方程求解,即可得到答案.
【解答】解:由题意可知,,,
设主桥拱半径为 ,
,
是半径,,
,
在中,,
,
解得.
故选:.
【点评】本题主要考查垂径定理的应用,涉及勾股定理,解题的关键是用勾股定理列出关于的方程解决问题.
三.圆周角定理(共3小题)
4.(2023 广西)如图,点,,,在上,.则的度数是
A. B. C. D.
【分析】由圆周角定理即可得到答案.
【解答】解:,,
.
故选:.
【点评】本题考查圆周角定理,关键是掌握圆周角定理.
5.(2023 武汉)如图,,,都是的半径,.
(1)求证:;
(2)若,,求的半径.
【分析】(1)利用圆周角定理可得,,结合可证明结论;
(2)过点作半径于点,可得,根据圆周角、弦、弧的关系可证得,即可求得,,利用勾股定理可求解,再利用勾股定理可求解圆的半径.
【解答】(1)证明:,,,
;
(2)解:过点作半径于点,连接,
,
,,
.
.
,,
,,
在 中,,
,
在中,,
,
解得,
即的半径是.
【点评】本题主要考查圆周角定理,勾股定理,垂径定理,圆心角、弦、弧的关系,掌握圆周角定理是解题的关键.
6.(2023 齐齐哈尔)综合与实践:
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在和中,,,,连接,,延长交于点.则与的数量关系:____,____;
(2)类比探究:如图2,在和中,,,,连接,,延长,交于点.请猜想与的数量关系及的度数,并说明理由;
(3)拓展延伸:如图3,和均为等腰直角三角形,,连接,,且点,,在一条直线上,过点作,垂足为点.则,,之间的数量关系:____;
(4)实践应用:正方形中,,若平面内存在点满足,,则____.
【分析】(1)根据等腰三角形的性质,利用证明即可得出结论;
(2)根据等腰三角形的性质,利用证明即可得出结论;
(3)根据等腰直角三角形的性质,利用证明即可得出结论;
(4)根据直径所对的圆周角是直角,先找到点,利用勾股定理计算出,再利用第3小题的结论得到三角形的高,的面积即可求出.
【解答】解:(1),,
理由如下:如图1所示:
和都是等腰三角形,
,,
又,
,
,
,
,
,
;
(2),,
理由如下:如图2所示:
证明:,
,
即,
又和都是等腰三角形,
,,
,
,
,,
,
;
(3),
理由如下:如图3所示:
和都是等腰三角形,
,,,
,
即:,
,
,
,,,
,
,
;
(4)如图4所示:
连接,以为直径作圆,
由题意,取满足条件的点,,则.,
,
,
连接,作于点,在上截取,
,,
,
,,
,
由(3)可得:,
,
,
同理可得:,
故的面积为:或.
【点评】本题是几何变换综合题,主要考查了全等三角形的判定,等腰三角形和等腰直角三角形的性质,圆周角定理,勾股定理,三角形的面积等知识,熟练掌握全等三角形的判定是解题的关键.
四.圆内接四边形的性质(共3小题)
7.(2023 西藏)如图,四边形内接于,为延长线上一点.若,则的度数是
A. B. C. D.
【分析】根据邻补角互补求出的度数,再根据圆内接四边形对角互补求出的度数,最后根据圆周角定理即可求出的度数.
【解答】解:,
,
四边形内接于,
,
,
,
故选:.
【点评】本题考查了圆内接四边形的性质、圆周角定理,熟练掌握这些定理和性质是解题的关键.
8.(2023 淮安)如图,四边形是的内接四边形,是的直径,,则的度数是 __120__.
【分析】连接,根据等边三角形的性质得到,再根据圆内接四边形的性质计算,得到答案.
【解答】解:如图,连接,
是的直径,,
,
为等边三角形,
,
四边形是的内接四边形,
,
,
故答案为:120.
【点评】本题考查的是圆内接四边形的性质、等边三角形的判定和性质,掌握圆内接四边形的对角互补是解题的关键.
9.(2023 北京)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证平分,并求的大小;
(2)过点作交的延长线于点,若,,求此圆半径的长.
【分析】(1)由圆周角定理得到,而,因此,得到平分,由圆内接四边形的性质得到,即可求出;
(2)由垂径定理推出是等边三角形,得到由,得到,由平行线的性质求出,由圆内接四边形的性质求出,得到,由直角三角形的性质得到,因为是圆的直径,即可得到圆半径的长是4.
【解答】(1)证明:,,
,
平分,
平分,
,
四边形是圆内接四边形,
,
,
,
,
;
(2)解:,,
,
,
,
是圆的直径,
垂直平分,
,
,
是等边三角形,
,
,
,
,
,
四边形是圆内接四边形,
,
,
,
,
,,
,
是圆的直径,
圆的半径长是4.
【点评】本题考查圆内接四边形的性质,圆周角定理,平行线的性质,等边三角形的判定和性质,关键是由圆内接四边形的性质得到,由垂径定理推出是等边三角形.
五.点与圆的位置关系(共1小题)
10.(2023 安徽)已知四边形内接于,对角线是的直径.
(1)如图1,连接,,若,求证:平分;
(2)如图2,为内一点,满足,.若,,求弦的长.
【分析】(1)由垂径定理证出,则可得出结论;
(2)延长交于,延长交于,证明四边形是平行四边形,则,根据勾股定理即可得出答案.
【解答】(1)证明:,
,
,
即平分;
(2)延长交于,延长交于,
,,
,
是的直径,
,
,,
,,
四边形是平行四边形,
,
.
【点评】本题主要考查了圆周角定理,垂径定理,勾股定理,平行四边形三角形的判定与性质,熟练掌握圆周角定理是解题的关键.
六.确定圆的条件(共1小题)
11.(2023 江西)如图,点,,,均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为
A.3个 B.4个 C.5个 D.6个
【分析】根据不在同一直线上的三点确定一个圆即可得到结论.
【解答】解:根据经过不在同一直线上的三点确定一个圆得,经过其中任意三个点,最多可画出圆的个数为6个,
故选:.
【点评】本题考查了确定圆的条件,熟练掌握不在同一直线上的三点确定一个圆是解题的关键.
七.三角形的外接圆与外心(共2小题)
12.(2023 台湾)如图的方格纸中,每个方格的边长为1,、两点皆在格线的交点上,今在此方格纸格线的交点上另外找两点、,使得的外心为,求的长度为何
A.4 B.5 C. D.
【分析】三角形外心的性质:三角形的外心到三角形三顶点的距离相等,由此得到,从而确定、的位置.
【解答】解:的外心为,
,
,
,
、是方格纸格线的交点,
、的位置如图所示,
.
故选:.
【点评】本题考查三角形的外接圆与外心,勾股定理,关键是掌握三角形的外心的性质.
13.(2023 盘锦)如图,内接于,为的直径,延长到点,使得,连接.过点作,交于点,交于点,过点作,交的延长线于点.
(1)求证:与相切.
(2)若,,求的长.
【分析】(1)连接,先证为等腰直角三角形得,由得,,再根据圆心角与圆周角的关系得,然后可得,据此即可得出结论;
(2)先由勾股定理求出,则,再求出,然后根据得,由此可求出,进而可求出,最后再证四边形为平行四边形即可得出的长.
【解答】(1)证明:连接,如图:
为的直径,
,
,
为等腰直角三角形,
,
,
,,
,
,
,
即:,
又点在上,
为的半径,
为的切线,
即:与相切.
(2)解:由(1)可知:,,,
在中,,,
由勾股定理得:,
,
,,,
,
设,,
,
,
,
,
在中,,,
由勾股定理得:,
,,
四边形为平行四边形,
.
【点评】此题主要考查了切线的判定,平行四边形的判定和性质,勾股定理,圆周角定理等,熟练掌握切线的判定,平行四边形的判定和性质,理解直径所对的圆周角是直角,在同圆或等圆中,同弧(或等弧)所对的圆心角是圆周角度数的2倍是解答此题的关键,
八.直线与圆的位置关系(共1小题)
14.(2023 盐城)如图,在中,是上(异于点,的一点,恰好经过点,,于点,且平分.
(1)判断与的位置关系,并说明理由.
(2)若,,求的半径长.
【分析】(1)连接,证明,进而可以解决问题;
(2)利用勾股定理求出,然后根据平行线分线段成比例定理即可求出半径.
【解答】解:(1)与相切,理由如下:
如图,连接,
,
,
平分,
,
,
,
,
,
是的半径,
与相切;
(2),,,
,
,
,
,
,
,
的半径长为.
【点评】本题考查了直线和圆的位置关系,勾股定理,平行线分线段成比例定理,切线的判定,平行线的性质,解决本题的关键是掌握切线的判定方法.
九.切线的性质(共4小题)
15.(2023 青岛)如图,在平面直角坐标系中,已知点,,过原点,且与轴交于另一点,为的切线,为切点,是的直径,则的度数为 __60__.
【分析】先根据点,的坐标得,进而得的半径为1,然后再在中利用锐角三角函数求出,进而得,最后再证为等边三角形即可求出的度数.
【解答】解:点,,
,
过原点,
为的半径,
为的切线,
,,
在中,,,,
,
,
,
又,
三角形为等边三角形,
,
即的度数为.
故答案为:60.
【点评】此题主要考查了点的坐标,切线的性质,锐角三角函数,等边三角形的判定和性质等,熟练掌握切线的性质,锐角三角函数的定义和等边三角形的判定和性质是解答此题的关键.
16.(2023 重庆)如图,是的切线,为切点,连接,.若,,,则的长度是
A.3 B. C. D.6
【分析】根据切线的性质得到,求得,得到,根据勾股定理即可得到结论.
【解答】解:连接,
是的切线,
,
,
,,
,
,
,
故选:.
【点评】本题考查了切线的性质,解直角三角形,正确的作出辅助线是解题的关键.
17.(2023 金华)如图,点在第一象限内,与轴相切于点,与轴相交于点,,连结,过点作于点.
(1)求证:四边形为矩形.
(2)已知的半径为4,,求弦的长.
【分析】(1)根据切线的性质得到轴根据垂直的定义得到,根据矩形的判定定理得到四边形是矩形;
(2)连接,根据矩形的性质得到,根据勾股定理得到,根据垂径定理即可得到结论.
【解答】(1)证明:与轴相切于点,
轴
又,,
,
四边形是矩形;
(2)解:连接,
四边形是矩形,
,
,
,
,
.
【点评】本题考查了切线的性质,矩形的判定和性质,勾股定理,垂径定理,正确都作出辅助线是解题的关键.
18.(2023 南通)如图,等腰三角形的顶角,和底边相切于点,并与两腰,分别相交于,两点,连接,.
(1)求证:四边形是菱形;
(2)若的半径为2,求图中阴影部分的面积.
【分析】(1)连接,根据切线的性质可得,然后利用等腰三角形的三线合一性质可得,从而可得和都是等边三角形,最后利用等边三角形的性质可得,即可解答;
(2)连接交于点,利用菱形的性质可得,,,然后在中,利用勾股定理求出的长,从而求出的长,最后根据图中阴影部分的面积扇形的面积菱形的面积,进行计算即可解答.
【解答】(1)证明:连接,
和底边相切于点,
,
,,
,
,,
和都是等边三角形,
,,
,
四边形是菱形;
(2)解:连接交于点,
四边形是菱形,
,,,
在中,,
,
,
图中阴影部分的面积扇形的面积菱形的面积
,
图中阴影部分的面积为.
【点评】本题考查了切线的性质,扇形面积的计算,等腰三角形的性质,菱形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
十.切线的判定(共2小题)
19.(2023 攀枝花)如图,为的直径,如果圆上的点恰使,求证:直线与相切.
【分析】由等腰三角形的性质和圆周角定理得出,则,再由切线的判定即可得出结论.
【解答】证明:如图,连接,
,
,
为的直径,
,
,
,
,
即,
,
是的半径,
直线与相切.
【点评】本题考查了切线的判定、圆周角定理、直角三角形的性质、等腰三角形的性质等知识;熟练掌握圆周角定理和切线的判定是解题的关键.
20.(2023 江西)如图,在中,,,以为直径的与相交于点,为上一点,且.
(1)求的长;
(2)若,求证:为的切线.
【分析】(1)由圆周角定理求出,由邻补角的性质的,由弧长公式即可求出的长.
(2)由圆周角定理得到,因此,得到,因此,得到直径,即可证明为的切线.
【解答】(1)解:,
,
,
,
半径长是2,
的长;
(2)证明:,
,
,
,
,
直径,
为的切线.
【点评】本题考查弧长的计算,切线的判定,圆周角定理,关键是由圆周角定理求出,得到的度数,即可求出的长,求出的度数,得到的度数,即可求出,从而证明为的切线.
十一.切线的判定与性质(共3小题)
21.(2023 鄂州)如图,为的直径,为上一点,点为的中点,过点作,交的延长线于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径长.
【分析】(1)连接,由等弧所对的圆周角相等得出,根据同圆的半径相等得出,于是有,可得出,再根据,即可得出,从而问题得证;
(2)连接,,先根据切割线定理求出的长,然后由勾股定理求出、的长,再根据等弧所对的弦相等得出,在中根据勾股定理求出的长,即可求出的半径.
【解答】(1)证明:连接,
点为的中点,
,
,
,
,
,
,
,
,
,
,
即,
又为的半径,
是的切线;
(2)解:连接,,
由(1)知是的切线,
,
,,
,
在中,由勾股定理得,
在中,由勾股定理得,
点是的中点,
,
,
为的直径,
,
由勾股定理得,
的半径长是2.5.
【点评】本题考查了切线的判定与性质,圆周角定理的推论,勾股定理,弧、弦之间的关系定理,熟练掌握这些定理是解题的关键.
22.(2023 东营)如图,在中,,以为直径的交于点,,垂足为.
(1)求证:是的切线;
(2)若,,求的长.
【分析】(1)连接,则,所以,由,得,则,所以,则,即可证明是的切线;
(2)连接,由是的直径,得,则,因为,,所以,可求得,再证明是等边三角形,则,而,根据弧长公式求出的长即可.
【解答】(1)证明:连接,则,
,
,
,
,
,
于点,
,
是的半径,,
是的切线.
(2)解:连接,
是的直径,
,
,
,,
,
,
,
,,
是等边三角形,
,
,
,
的长是.
【点评】此题重点考查等腰三角形的性质、平行线的判定与性质、切线的判定定理等知识,证明是解题的关键.
23.(2023 眉山)如图,中,以为直径的交于点,平分,过点作于点,延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
【分析】(1)连接,证明,即可得到结论;
(2)根据锐角三角函数先求出半径和的长,然后证明,,进而根据线段的和差即可解决问题.
【解答】(1)证明:如图,连接,
平分,
,
,
,
,
,
,
,
是的半径,
是的切线;
(2)解:,,,
,
,
,
,
在中,,
,
为的直径,
,
平分,
,
,
,
,
,
的长为.
【点评】本题考查切线的判定和性质,全等三角形的判定和性质、等腰三角形的性质、圆周角定理、解题的关键是学会添加常用辅助线,构造基本图形解决问题.
十二.正多边形和圆(共3小题)
24.(2023 福建)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为,若用圆内接正十二边形作近似估计,可得的估计值为
A. B. C.3 D.
【分析】过作于,求得,根据直角三角形的性质得到,根据三角形的面积公式得到,于是得到正十二边形的面积为,根据圆的面积公式即可得到结论.
【解答】解:如图,是正十二边形的一条边,点是正十二边形的中心,
过作于,
在正十二边形中,,
,
,
正十二边形的面积为,
,
,
的近似值为3,
故选:.
【点评】本题考查了正多边形与圆,三角形的面积的计算,正确地作出辅助线是解题的关键.
25.(2023 衡阳)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 __10__.
【分析】先求出多边形的每一个内角为,可得到,即可求解.
【解答】解:多边形是正五边形,
正五边形的每一个内角为:,
,
正五边形的个数是.
故答案为:10.
【点评】本题主要考查正多边形与圆,多边形内角和问题,熟练掌握相关知识点是解题关键.
26.(2023 上海)如果一个正多边形的中心角是,那么这个正多边形的边数为 __18__.
【分析】根据正边形的中心角的度数为进行计算即可得到答案.
【解答】解:.
故这个正多边形的边数为18.
故答案为:18.
【点评】本题考查的是正多边形内角、外角和中心角的知识,掌握中心角的计算公式是解题的关键.
十三.弧长的计算(共3小题)
27.(2023 青岛)如图,四边形是的内接四边形,,.若的半径为5,则的长为
A. B. C. D.
【分析】根据圆周角的性质,计算出弧所对的圆心角度数,按照公式求出弧长即可.
【解答】解:连接、、,
,.
,,
,
.
故选:.
【点评】本题考查了弧长的计算和圆周角定理,同弧所对的圆周角是圆心角的一半.
28.(2023 吉林)如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角,则的长为 ____.(结果保留
【分析】由弧长公式:是弧长,是扇形圆心角的度数,是扇形的半径长),由此即可计算.
【解答】解:,半径为,
的长.
故答案为:.
【点评】本题考查弧长的计算,关键是掌握弧长公式.
29.(2023 镇江)如图,扇形的半径为1,分别以点、为圆心,大于的长为半径画弧,两弧相交于点,,则的长____(结果保留.
【分析】由等腰三角形的性质求出的度数,由弧长公式即可计算.
【解答】解:由作图知:垂直平分,
,
,
扇形的半径是1,
的长.
故答案为:.
【点评】本题考查弧长的计算,关键是掌握弧长公式.
十四.扇形面积的计算(共1小题)
30.(2023 滨州)如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆,,相互经过彼此的圆心,则图中三个阴影部分的面积之和为
A. B. C. D.
【分析】根据扇形面积的计算方法进行计算即可.
【解答】解:如图,连接,,,,,,,,,则△,△,△,△是边长为1的正三角形,
所以,
,
故选:.
【点评】本题考查扇形面积的计算,掌握扇形面积的计算方法是正确解答的前提.
十五.圆锥的计算(共3小题)
31.(2023 东营)如果圆锥侧面展开图的面积是,母线长是5,则这个圆锥的底面半径是
A.3 B.4 C.5 D.6
【分析】根据圆锥的侧面积底面周长母线长即可求出答案.
【解答】解:设底面半径为,则底面周长,圆锥的侧面展开图的面积,
.
故选:.
【点评】本题考查了圆锥的计算,利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.
32.(2023 齐齐哈尔)若圆锥的底面半径长,母线长,则该圆锥的侧面积为 __6___.(结果保留
【分析】解析圆锥的侧面积底面周长母线长,把相应数值代入即可求解.
【解答】解:圆锥的侧面积
故答案为:.
【点评】本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.
33.(2023 宿迁)若圆锥的底面半径为,侧面展开图是一个圆心角为的扇形,则这个圆锥的母线长是 __6__.
【分析】设圆锥的母线长为,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到,然后解关于的方程即可.
【解答】解:设圆锥的母线长为,
根据题意得,
解得,
即圆锥的母线长为.
故答案为6.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
十六.圆的综合题(共4小题)
34.(2023 枣庄)如图,为的直径,点是的中点,过点作射线的垂线,垂足为.
(1)求证:是的切线;
(2)若,,求的长;
(3)在(2)的条件下,求阴影部分的面积(用含有的式子表示).
【分析】(1)连接,证明,即可得到结论.
(2)连接,证明,从而可得,再代入求值即可.
(3)连接,,证明,从而可得,求出扇形的面积即可得到阴影部分的面积.
【解答】(1)证明:如图,连接,
点是的中点,
,
,
,
,
,
,
,
半径,
是的切线.
(2)解:如图,连接,
为的直径,
,
,
,
,
,
,
.
答:的长为.
(3)解:如图,连接、,
,
,
在中,,
,
,
,
,
,
是等边三角形,
,
,
,
,
.
答:阴影部分的面积为.
【点评】本题考查了圆的综合应用,熟练掌握切线的判断定理以及扇形面积的求法是解题的关键.
35.(2023 兰州)如图,内接于,是的直径,,于点,交于点,交于点,,连接.
(1)求证:是的切线;
(2)判断的形状,并说明理由;
(3)当时,求的长.
【分析】(1)连接,由圆周角定理得出,由等腰三角形的性质证出,由切线的判定可得出结论;
(2)由垂径定理得出,,证出,由直角三角形的性质得出,则可得出结论;
(3)由(2)可知,,,则可得出答案.
【解答】(1)证明:连接,
,
,
,
,
,
又,
,
又,
,
,
,
,
,
为半径,
是的切线;
(2)解:为等腰三角形,
理由:,
,,
,
,
,
,
又,
,
又,
,
,
,,
,
,
即为等腰三角形;
(3)解:由(2)可知,,,
,
,
.
【点评】本题是圆的综合题,考查了圆周角定理,切线的判定与性质,垂径定理,等腰三角形的判定与性质,直角三角形的性质,熟练掌握切线的判定是解题的关键.
36.(2023 杭州)如图,在中,直径垂直弦于点,连接,,,作于点,交线段于点(不与点,重合),连接.
(1)若,求的长.
(2)求证:.
(3)若,猜想的度数,并证明你的结论.
【分析】(1)由垂径定理可得,结合可得,根据圆周角定理可得,进而可得,通过证明,可得;
(2)证明,根据对应边成比例可得,再根据,,可证;
(3)方法一:设,,可证,,通过证明,进而可得,即,则.方法二:延长交于点,连接,证明是等腰直角三角形,即可解决问题.
【解答】(1)解:直径垂直弦,
,
,
,
,
,
由圆周角定理得,
,
在和中,
,
,
;
(2)证明:是的直径,
,
,
,
,
,
,
由(1)知,
,
,
;
(3)解:,证明如下:
解法一:如图,连接,
,
,
直径垂直弦,
,,
,
,
,
设,,
则,
,
,
,
,
,,,
,
,
,
,
,
在和中,
,
,
,
即,
,
.
解法二:
如图,延长交于点,连接,
,
,
,
,
是的直径,
,
,
,
,
,
,
是等腰直角三角形,
.
【点评】本题是圆的综合题,考查垂径定理,圆周角定理,全等三角形的判定与性质,相似三角形的判定与性质,等腰三角形的性质等,难度较大,解题的关键是综合应用上述知识点,特别是第3问,需要大胆猜想,再逐步论证.
37.(2023 泰州)已知:、为圆上两定点,点在该圆上,为所对的圆周角.
知识回顾
(1)如图①,中,、位于直线异侧,.
①求的度数;
②若的半径为5,,求的长;
逆向思考
(2)如图②,若为圆内一点,且,,.求证:为该圆的圆心;
拓展应用
(3)如图③,在(2)的条件下,若,点在位于直线上方部分的圆弧上运动.点在上,满足的所有点中,必有一个点的位置始终不变.请证明.
【分析】(1)①根据,结合圆周角定理求的度数;
②构造直角三角形;
(2)只要说明点到圆上、和另一点的距离相等即可;
(3)根据,构造一条线段等于,利用三角形全等来说明此线段和相等.
【解答】(1)解:①,,
,
.
②连接,过作,垂足为,
,,
是等腰直角三角形,且,
,,
是等腰直角三角形,
,
在直角三角形中,,
.
(2)延长交圆于点,则,
,
,
,
,
,
,
,
为该圆的圆心.
(3)过作的垂线交的延长线于点,连接,延长交圆于点,连接,,
,
,
是等腰直角三角形,
,
,,
,
是直径,
,
,
,
,
,
,
,
必有一个点的位置始终不变,点即为所求.
【点评】本题考查了圆周角定理,并对圆周角定理的逆命题进行了创新,还考查了解直角三角形和三角形全等的知识,对于(3)构造一条线段等于是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
