知识必备12 相似三角形(知识清单 易错清单 11个考试清单真题专练)(含解析)
文档属性
| 名称 | 知识必备12 相似三角形(知识清单 易错清单 11个考试清单真题专练)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
知识必备12 相似三角形
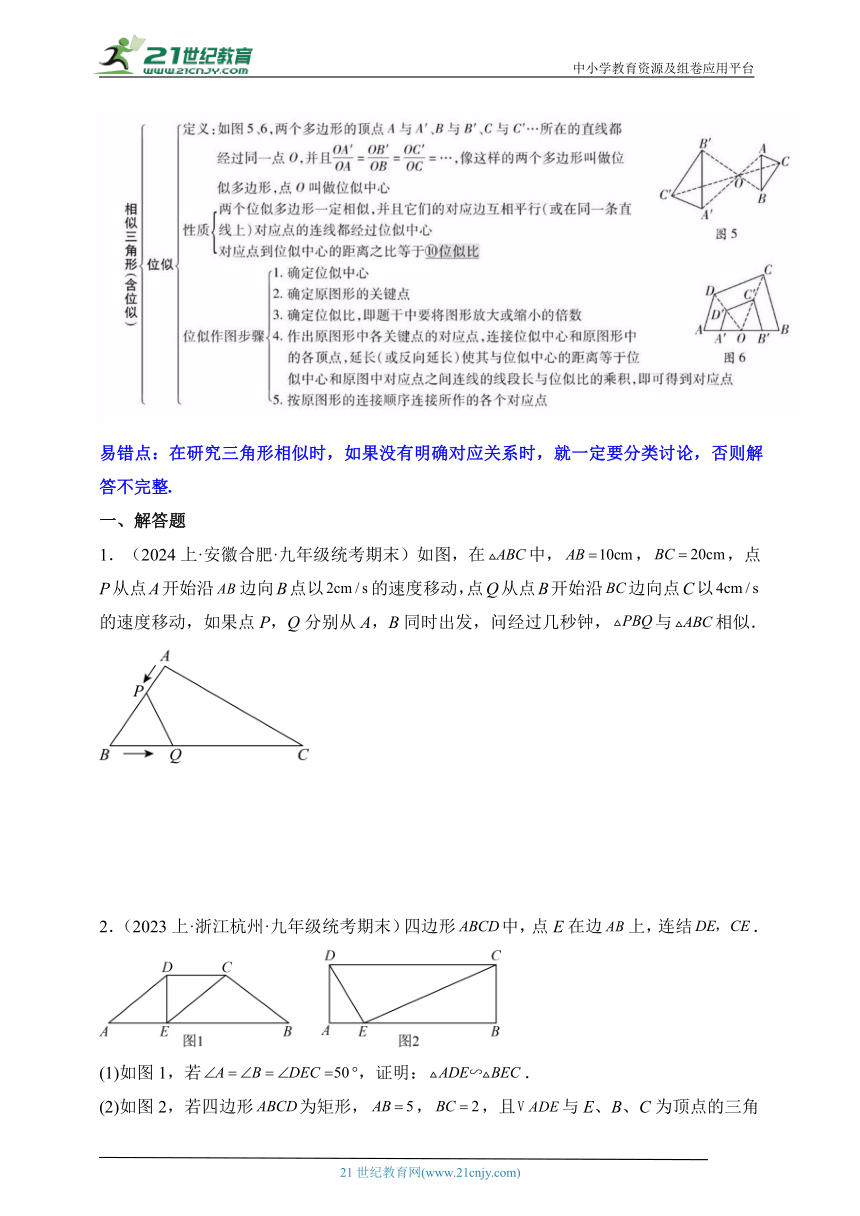
易错点:在研究三角形相似时,如果没有明确对应关系时,就一定要分类讨论,否则解答不完整.
一、解答题
1.(2024上·安徽合肥·九年级统考期末)如图,在中,,,点P从点A开始沿边向B点以的速度移动,点Q从点B开始沿边向点C以的速度移动,如果点P,Q分别从A,B同时出发,问经过几秒钟,与相似.
2.(2023上·浙江杭州·九年级统考期末)四边形中,点E在边上,连结.
(1)如图1,若,证明:.
(2)如图2,若四边形为矩形,,,且与E、B、C为顶点的三角形相似,求的长.
3.(2024上·陕西宝鸡·九年级宝鸡市新建路中学校考期末)如图,在中,,,,点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动.若点、点同时出发,当某点到终点时,另一点立即停止运动.运动时间为.
(1)_________,_________;(用含的代数式表示)
(2)请计算当点运动多少秒时,以、、为顶点的三角形与相似.
4.(湖南省常德市初中教学联盟校2023-2024学年九年级上学期期末数学试题)综合与实践
如图,在中,,点P以每秒2个单位长度的速度从点A出发,沿方向向终点B匀速运动,同时点Q以每秒1个单位长度的速度从点C出发,沿方向向终点A匀速运动,连接.设运动的时间为t秒.
(1)求的长(用含t的代数式表示).
(2)当秒时,求的面积.
(3)如图2,连接,当为直角三角形时,求所有满足条件t的值.
一.比例的性质(共2小题)
1.(2023 金昌)若,则
A.6 B. C.1 D.
2.(2023 甘孜州)若,则____.
二.黄金分割(共1小题)
3.(2023 广东)我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了
A.黄金分割数 B.平均数 C.众数 D.中位数
三.平行线分线段成比例(共3小题)
4.(2023 吉林)如图,在中,点在边上,过点作,交于点.若,,则的值是
A. B. C. D.
5.(2023 常州)小明按照以下步骤画线段的三等分点:
画法 图形
(1)以为端点画一条射线; (2)用圆规在射线上依次截取3条等长线段、、,连接; (3)过点、分别画的平行线,交线段于点、.、就是线段的三等分点.
这一画图过程体现的数学依据是
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
6.(2023 北京)如图,直线,交于点,,若,,,则的值为 ____.
四.相似图形(共1小题)
7.(2023 泰州)两个相似图形的周长比为,则面积比为 ____.
五.相似多边形的性质(共1小题)
8.(2023 威海)如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为.若矩形与原矩形相似,,则的长为
A. B. C. D.
六.相似三角形的性质(共2小题)
9.(2023 重庆)如图,已知,,若的长度为6,则的长度为
A.4 B.9 C.12 D.13.5
10.(2023 重庆)若两个相似三角形周长的比为,则这两个三角形对应边的比是
A. B. C. D.
七.相似三角形的判定(共1小题)
11.(2023 大庆)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为,点对应的点记为点,若点恰好落在边上,则图中与一定相似的三角形是 ____.
八.相似三角形的判定与性质(共7小题)
12.(2023 雅安)如图,在中,是上一点,交于点,的延长线交的延长线于点,,,则的长为
A.4 B.6 C.8 D.10
13.(2023 哈尔滨)如图,,相交于点,,是的中点,,交于点,若,,则的长为
A.2 B.4 C.6 D.8
14.(2023 乐山)如图,在平行四边形中,是线段上一点,连结、交于点.若,则____.
15.(2023 江西)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的.“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点,,在同一水平线上,和均为直角,与相交于点.测得,,,则树高____.
16.(2023 邵阳)如图,,,点是线段上的一点,且.已知,,.
(1)证明:.
(2)求线段的长.
17.(2023 眉山)如图,中,点是的中点,连结并延长交的延长线于点.
(1)求证:;
(2)点是线段上一点,满足,交于点,若,,求的长.
18.(2023 苏州)如图,是的内接三角形,是的直径,,,点在上,连接并延长,交于点,连接,作,垂足为.
(1)求证:;
(2)若,求的长.
九.相似三角形的应用(共2小题)
19.(2023 南充)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为
A. B. C. D.
20.(2023 镇江)如图,用一个卡钳测量某个零件的内孔直径,量得长度为,则等于 ____.
十.位似变换(共5小题)
21.(2023 朝阳)如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为2,把放大,则点的对应点的坐标是
A. B.或
C. D.或
22.(2023 遂宁)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点、成位似关系,则位似中心的坐标为
A. B. C. D.
23.(2023 烟台)如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点为位似中心作正方形,正方形,,按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为,,,,则顶点的坐标为
A. B. C. D.
24.(2023 阜新)如图,和是以点为位似中心的位似图形,相似比为,则和的面积比是 ____.
25.(2023 盘锦)如图,的顶点坐标是,,,以点为位似中心,将缩小为原来的,得到△,则点的坐标为 ____.
十一.相似形综合题(共1小题)
26.(2023 福建)如图1,在中,,,是边上不与,重合的一个定点.于点,交于点.是由线段绕点顺时针旋转得到的,,的延长线相交于点.
(1)求证:;
(2)求的度数;
(3)若是的中点,如图2,求证:.
知识必备12 相似三角形
易错点:在研究三角形相似时,如果没有明确对应关系时,就一定要分类讨论,否则解答不完整.
一、解答题
1.(2024上·安徽合肥·九年级统考期末)如图,在中,,,点P从点A开始沿边向B点以的速度移动,点Q从点B开始沿边向点C以的速度移动,如果点P,Q分别从A,B同时出发,问经过几秒钟,与相似.
【答案】经过秒或秒钟,与相似.
【分析】本题考查相似三角形的性质,设经过秒钟时,与相似,得到,,,讨论对应边的不同,分别利用相似三角形对应边成比例,建立方程求解即可.
【详解】解:设经过秒钟,与相似.
由题意得,,
,,
,,
与相似,
当与对应时,有,即,解得,
当与对应时,有,即,解得,
综上所述,经过秒或秒钟,与相似.
2.(2023上·浙江杭州·九年级统考期末)四边形中,点E在边上,连结.
(1)如图1,若,证明:.
(2)如图2,若四边形为矩形,,,且与E、B、C为顶点的三角形相似,求的长.
【答案】(1)见解析
(2)或1或4
【分析】本题考查相似三角形的判定与性质、矩形的性质等知识.
(1)由点E在边上,且,得,,所以,又因为,所以根据“有两个角分别相等的两个三角形相似”即可证明;
(2)分两种情况:或,设,根据相似三角形的对应边成比例列方程求出x的值即可.
【详解】(1)证明:∵点E在边上,且,
∴,,
∴,
∵,
∴;
(2)如图2、如图3,
分两种情况:
设,
∵,
当时,
∴,
∴,
解得;
时,
∴,
∴,
解得:,
综上,或1或4.
3.(2024上·陕西宝鸡·九年级宝鸡市新建路中学校考期末)如图,在中,,,,点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动.若点、点同时出发,当某点到终点时,另一点立即停止运动.运动时间为.
(1)_________,_________;(用含的代数式表示)
(2)请计算当点运动多少秒时,以、、为顶点的三角形与相似.
【答案】(1);
(2)秒或秒
【分析】本题考查相似三角形的判定和性质,三角形的面积,
(1)根据路程=速度×时间以及线段的和差,即可列出代数式;
(2)分两种情况,或,分别得到关于的方程,求出的值,即可解决问题;
掌握相似三角形的判定和性质是解题的关键.
【详解】(1)解:∵点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动,,,
∴,,
故答案为:;;
(2)设点运动秒时,以、、为顶点的三角形与相似,
∵点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动,点、点同时出发,当某点到终点时,另一点立即停止运动,,,
∴点运动到终点所需时间为:,
点运动到终点所需时间为:,
∴的取值范围是:,
∵,
∴可分两种情况:
当时,
∴,
∴,
∴;
当时,
∴,
∴,
∴;
∴当点运动2.4秒或秒时,以、、为顶点的三角形与相似.
4.(湖南省常德市初中教学联盟校2023-2024学年九年级上学期期末数学试题)综合与实践
如图,在中,,点P以每秒2个单位长度的速度从点A出发,沿方向向终点B匀速运动,同时点Q以每秒1个单位长度的速度从点C出发,沿方向向终点A匀速运动,连接.设运动的时间为t秒.
(1)求的长(用含t的代数式表示).
(2)当秒时,求的面积.
(3)如图2,连接,当为直角三角形时,求所有满足条件t的值.
【答案】(1)
(2)9
(3)或
【分析】本题考查了勾股定理解直角三角形,相似三角形的性质与判定等知识,熟知相关知识并根据题意添加适当辅助线构造直角三角形运用勾股定理或相似三角形是解题关键,第(3)步要注意分类讨论.
(1)根据勾股定理求出,根据题意即可表示出;
(2)作,根据题意得到,,证明,求出,根据三角形面积公式即可求出;
(3)先表示出,,,,分和两种情况,分别根据勾股定理和相似三角形的判定和性质即可求解.
【详解】(1)解:在中,由勾股定理可得,
由题意可得:,则;
(2)解:如图,作,
由题意可得:,,
∵,
∴,
∵,
∴,
∴,
即,
解得,
;
(3)解:由题意可得:,,,,
①如图2,当时,根据勾股定理得,,
∴,
∴
解得:,符合题意;
②如图3,当时,作垂足为E,
由(1)得,
∴,
即,
∴,,
∴.
∵,
∴,
∴,
∴,
,
,
即,
解得,(不合题意,舍去).
∴或.
一.比例的性质(共2小题)
1.(2023 金昌)若,则
A.6 B. C.1 D.
【分析】直接利用比例的性质,内项之积等于外项之积即可得出答案.
【解答】解:,
.
故选:.
【点评】此题主要考查了比例的性质,正确将原式变形是解题关键.
2.(2023 甘孜州)若,则__1__.
【分析】根据比例的性质解答即可.
【解答】解:,
.
故答案为:1.
【点评】本题考查了比例的性质,解决本题的关键是掌握比例的性质.
二.黄金分割(共1小题)
3.(2023 广东)我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了
A.黄金分割数 B.平均数 C.众数 D.中位数
【分析】根据黄金分割的定义,即可解答.
【解答】解:我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了黄金分割数,
故选:.
【点评】本题考查了黄金分割,算术平均数,中位线,众数,统计量的选择,熟练掌握这些数学知识是解题的关键.
三.平行线分线段成比例(共3小题)
4.(2023 吉林)如图,在中,点在边上,过点作,交于点.若,,则的值是
A. B. C. D.
【分析】由,利用平行线分线段成比例,可得出,再代入,,,即可求出结论.
【解答】解:,
.
故选:.
【点评】本题考查了平行线分线段成比例,牢记“平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例”是解题的关键.
5.(2023 常州)小明按照以下步骤画线段的三等分点:
画法 图形
(1)以为端点画一条射线; (2)用圆规在射线上依次截取3条等长线段、、,连接; (3)过点、分别画的平行线,交线段于点、.、就是线段的三等分点.
这一画图过程体现的数学依据是
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
【分析】根据平行线分线段成比例定理解答即可.
【解答】解:,
,
,
,
这一画图过程体现的数学依据是两条直线被一组平行线所截,所得的对应线段成比例,
故选:.
【点评】本题考查的是平行线分线段成比例定理,尺规作图,掌握平行线分线段成比例定理是解题的关键.
6.(2023 北京)如图,直线,交于点,,若,,,则的值为 ____.
【分析】根据题意求出,再根据平行线分线段成比例定理计算即可.
【解答】解:,,
,
,
,
故答案为:.
【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
四.相似图形(共1小题)
7.(2023 泰州)两个相似图形的周长比为,则面积比为 ____.
【分析】由两个相似图形,其周长之比为,根据相似图形的周长的比等于相似比,即可求得其相似比,又由相似图形的面积的比等于相似比的平方,即可求得答案.
【解答】解:两个相似图形,其周长之比为,
其相似比为,
其面积比为.
故答案为:.
【点评】此题考查了相似图形的性质.此题比较简单,注意熟记定理是关键.
五.相似多边形的性质(共1小题)
8.(2023 威海)如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为.若矩形与原矩形相似,,则的长为
A. B. C. D.
【分析】设,根据矩形的性质可得,,再根据折叠的性质可得:,,,从而可得四边形是正方形,然后利用正方形的性质可得,最后利用相似多边形的性质,进行计算即可解答.
【解答】解:设,
四边形是矩形,
,,
由折叠得:,,,
四边形是矩形,
,
四边形是正方形,
,
矩形与原矩形相似,
,
,
解得:或,
经检验:或都是原方程的根,
,
,
,
故选:.
【点评】本题考查了相似多边形的性质,解一元二次方程公式法,矩形的性质,翻折变换(折叠问题),正方形的判定与性质熟练掌握相似多边形的性质是解题的关键.
六.相似三角形的性质(共2小题)
9.(2023 重庆)如图,已知,,若的长度为6,则的长度为
A.4 B.9 C.12 D.13.5
【分析】根据相似三角形的性质列出方程即可求解.
【解答】解:,.
,
当时,.
故选:.
【点评】本题主要考查了相似三角形的性质,找到对应的边成比例是解题的关键.
10.(2023 重庆)若两个相似三角形周长的比为,则这两个三角形对应边的比是
A. B. C. D.
【分析】根据相似三角形的性质:相似三角形周长的比等于相似比,求解即可.
【解答】解:两个相似三角形周长的比为,
这两个三角形对应边的比为,
故选:.
【点评】本题考查了相似三角形的性质,熟练掌握相似三角形的性质是解题的关键.
七.相似三角形的判定(共1小题)
11.(2023 大庆)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为,点对应的点记为点,若点恰好落在边上,则图中与一定相似的三角形是 ____.
【分析】利用矩形的性质得到,然后利用折叠的性质推导出,进而得到,由此推断出.
【解答】解:四边形是矩形,
,
,由折叠的性质可知,,
,
,
,
故答案为:.
【点评】本题主要考查了相似三角形的判定、矩形的性质以及翻折变换(折叠问题),熟练掌握相似三角形的判定方法是解答本题的关键:两角法:有两组角对应相等的两个三角形相似.
八.相似三角形的判定与性质(共7小题)
12.(2023 雅安)如图,在中,是上一点,交于点,的延长线交的延长线于点,,,则的长为
A.4 B.6 C.8 D.10
【分析】根据平行四边形的性质得出,,,于是推出,,先求出与的比值,继而得出与的比值,再根据相似三角形对应边成比例即可求出的长.
【解答】解:四边形是平行四边形,
,,,
,
,
,
,,
,
即,
,
,
,
,
,,
,
,
,
故选:.
【点评】本题考查了平行四边形的性质和相似三角形的判定与性质,熟练掌握这些图形的性质是解题的关键.
13.(2023 哈尔滨)如图,,相交于点,,是的中点,,交于点,若,,则的长为
A.2 B.4 C.6 D.8
【分析】由易得,根据相似三角形的性质可得,于是,求出,易得为的中位线,则.
【解答】解:,
,
,
,
,
,
,
,
,
,是的中点,
为的中位线,
.
故选:.
【点评】本题主要考查相似三角形的判定与性质、三角形中位线定理,熟记“8”字模型相似三角形,以及三角形中位线定理是解题关键.
14.(2023 乐山)如图,在平行四边形中,是线段上一点,连结、交于点.若,则____.
【分析】通过证明,可得,即可求解.
【解答】解:四边形是平行四边形,
,,
,
设,则,
,
,
,
,
,
故答案为:.
【点评】本题考查了相似三角形的判定和性质,平行四边形的性质,证明三角形相似是解题的关键.
15.(2023 江西)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的.“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点,,在同一水平线上,和均为直角,与相交于点.测得,,,则树高__6__.
【分析】根据题意可知:,从而可以得到,然后代入数据计算,即可得到的长.
【解答】解:由题意可得,
,,,,
,
,
即,
解得,
树高,
故答案为:6
【点评】本题考查相似三角形的判定与性质,解答本题的关键是明确题意,利用数形结合的思想解答.
16.(2023 邵阳)如图,,,点是线段上的一点,且.已知,,.
(1)证明:.
(2)求线段的长.
【分析】(1)利用同角的余角相等得,可证明结论;
(2)根据相似三角形的性质即可求出答案.
【解答】(1)证明:,,,
,
,,
,
;
(2)解:,
,
,
.
【点评】本题主要考查了相似三角形的性质和判定,利用同角的余角相等得是解决问题的关键.
17.(2023 眉山)如图,中,点是的中点,连结并延长交的延长线于点.
(1)求证:;
(2)点是线段上一点,满足,交于点,若,,求的长.
【分析】(1)先根据证明,得,再根据平行线分线段成比例定理可得结论;
(2)先根据(1)可得:,由平行线的性质和等腰三角形的判定可得,证明,列比例式可得的长.
【解答】(1)证明:四边形是平行四边形,
,,
,,
是的中点,
,
,
,
,
,
;
(2)解:,,
,
,
四边形是平行四边形,
,
,,
,
,
,
,
,即,
.
【点评】本题考查平行四边形的性质,相似三角形的性质和判定,全等三角形的性质和判定等知识,掌握三角形全等和相似的性质和判定是解本题的关键.
18.(2023 苏州)如图,是的内接三角形,是的直径,,,点在上,连接并延长,交于点,连接,作,垂足为.
(1)求证:;
(2)若,求的长.
【分析】(1)根据圆周角定理得,进而可以证明结论;
(2)过点作,垂足为,证明,得,代入值即可解决问题.
【解答】(1)证明:为直径,
,
,
,
所对的圆周角为和,
,
;
(2)解:如图,过点作,垂足为,
,,,
,
,
,
,
,
,
,
,
,
,
,
.
【点评】本题考查圆周角定理、相似三角形的判定与性质、解直角三角形、勾股定理等知识点,解决本题的关键是得到.
九.相似三角形的应用(共2小题)
19.(2023 南充)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为
A. B. C. D.
【分析】根据镜面反射的性质,,再根据相似三角形对应边成比例列式求解即可.
【解答】解:如图:
,,
,
,
,
,
即,
,
故选:.
【点评】本题考查了相似三角形的应用.应用镜面反射的基本性质,得出三角形相似,再运用相似三角形对应边成比例即可解答.
20.(2023 镇江)如图,用一个卡钳测量某个零件的内孔直径,量得长度为,则等于 __18__.
【分析】根据相似三角形的判定和性质,可以求得的长.
【解答】解:,,
,
,
,
,
故答案为:18.
【点评】本题考查相似三角形的应用,求出的值是解答本题的关键.
十.位似变换(共5小题)
21.(2023 朝阳)如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为2,把放大,则点的对应点的坐标是
A. B.或
C. D.或
【分析】根据位似变换的性质计算,得到答案.
【解答】解:以原点为位似中心,相似比为2,把放大,点的坐标为,
点的对应点的坐标为或,,即或,
故选:.
【点评】本题考查的是位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或.
22.(2023 遂宁)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点、成位似关系,则位似中心的坐标为
A. B. C. D.
【分析】根据位似中心的定义作答.
【解答】解:如图:
与的对应顶点的连线相交于点,则位似中心的坐标为.
故选:.
【点评】本题主要考查了位似变换,坐标与图形性质,解题的关键是掌握“位似中心”的确定方法.
23.(2023 烟台)如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点为位似中心作正方形,正方形,,按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为,,,,则顶点的坐标为
A. B. C. D.
【分析】根据位似变换的概念、点的坐标的变化情况找出点的横纵坐标的变化规律,根据规律解答即可.
【解答】解:由题意可知:点,点,点,
,,,,,,,,,,,
顶点的坐标为,即,
故选:.
【点评】本题考查的是位似变换、点的坐标的变化规律,根据点的坐标的变化情况正确找出规律是解题的关键.
24.(2023 阜新)如图,和是以点为位似中心的位似图形,相似比为,则和的面积比是 ____.
【分析】先利用位似的性质得到,相似比为,然后根据相似三角形的性质解决问题.
【解答】解:与是以点为位似中心的位似图形,位似比为,
,相似比为,
与的面积之比为.
故答案为:.
【点评】本题考查的是位似变换的概念和性质、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.
25.(2023 盘锦)如图,的顶点坐标是,,,以点为位似中心,将缩小为原来的,得到△,则点的坐标为 __,或,__.
【分析】根据位似变换的性质计算,得到答案.
【解答】解:以原点为位似中心,把缩小为原来的,可以得到△,点的坐标为,
点的坐标是,或,,即,或,.
故答案为:,或,.
【点评】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或.
十一.相似形综合题(共1小题)
26.(2023 福建)如图1,在中,,,是边上不与,重合的一个定点.于点,交于点.是由线段绕点顺时针旋转得到的,,的延长线相交于点.
(1)求证:;
(2)求的度数;
(3)若是的中点,如图2,求证:.
【分析】(1)由是由线段绕点顺时针旋转 得到的,得,,,又,,可得,根据,有,故;
(2)设与的交点为,由,,有,,即,可得,即得,从而;
(3)延长交于点,连接,,由,知,,而是的中点,有,可得,从而,,可证,,得,,即可得,故.
【解答】(1)证明:如图:
是由线段绕点顺时针旋转 得到的,
,,,
,,
.
,
,
,
,
,
;
(2)解:设与的交点为,如图:
,,
,
,即,
,
,
,
,
,
,
;
(3)证明:延长交于点,连接,,如图:
,
,
.
是的中点,
,
,
,
,,
,,,
,
,
由(2)知,,
.
,
,
,,
,即,
,
,
.
【点评】本题考查相似三角形综合应用,涉及三角形内角和定理、平行线的判定与性质、全等三角形的判定与性质、等腰三角形及直角三角形的判定与性质等基础知识,解题的关键是掌握相似三角形的判定与性质定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
知识必备12 相似三角形
易错点:在研究三角形相似时,如果没有明确对应关系时,就一定要分类讨论,否则解答不完整.
一、解答题
1.(2024上·安徽合肥·九年级统考期末)如图,在中,,,点P从点A开始沿边向B点以的速度移动,点Q从点B开始沿边向点C以的速度移动,如果点P,Q分别从A,B同时出发,问经过几秒钟,与相似.
2.(2023上·浙江杭州·九年级统考期末)四边形中,点E在边上,连结.
(1)如图1,若,证明:.
(2)如图2,若四边形为矩形,,,且与E、B、C为顶点的三角形相似,求的长.
3.(2024上·陕西宝鸡·九年级宝鸡市新建路中学校考期末)如图,在中,,,,点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动.若点、点同时出发,当某点到终点时,另一点立即停止运动.运动时间为.
(1)_________,_________;(用含的代数式表示)
(2)请计算当点运动多少秒时,以、、为顶点的三角形与相似.
4.(湖南省常德市初中教学联盟校2023-2024学年九年级上学期期末数学试题)综合与实践
如图,在中,,点P以每秒2个单位长度的速度从点A出发,沿方向向终点B匀速运动,同时点Q以每秒1个单位长度的速度从点C出发,沿方向向终点A匀速运动,连接.设运动的时间为t秒.
(1)求的长(用含t的代数式表示).
(2)当秒时,求的面积.
(3)如图2,连接,当为直角三角形时,求所有满足条件t的值.
一.比例的性质(共2小题)
1.(2023 金昌)若,则
A.6 B. C.1 D.
2.(2023 甘孜州)若,则____.
二.黄金分割(共1小题)
3.(2023 广东)我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了
A.黄金分割数 B.平均数 C.众数 D.中位数
三.平行线分线段成比例(共3小题)
4.(2023 吉林)如图,在中,点在边上,过点作,交于点.若,,则的值是
A. B. C. D.
5.(2023 常州)小明按照以下步骤画线段的三等分点:
画法 图形
(1)以为端点画一条射线; (2)用圆规在射线上依次截取3条等长线段、、,连接; (3)过点、分别画的平行线,交线段于点、.、就是线段的三等分点.
这一画图过程体现的数学依据是
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
6.(2023 北京)如图,直线,交于点,,若,,,则的值为 ____.
四.相似图形(共1小题)
7.(2023 泰州)两个相似图形的周长比为,则面积比为 ____.
五.相似多边形的性质(共1小题)
8.(2023 威海)如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为.若矩形与原矩形相似,,则的长为
A. B. C. D.
六.相似三角形的性质(共2小题)
9.(2023 重庆)如图,已知,,若的长度为6,则的长度为
A.4 B.9 C.12 D.13.5
10.(2023 重庆)若两个相似三角形周长的比为,则这两个三角形对应边的比是
A. B. C. D.
七.相似三角形的判定(共1小题)
11.(2023 大庆)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为,点对应的点记为点,若点恰好落在边上,则图中与一定相似的三角形是 ____.
八.相似三角形的判定与性质(共7小题)
12.(2023 雅安)如图,在中,是上一点,交于点,的延长线交的延长线于点,,,则的长为
A.4 B.6 C.8 D.10
13.(2023 哈尔滨)如图,,相交于点,,是的中点,,交于点,若,,则的长为
A.2 B.4 C.6 D.8
14.(2023 乐山)如图,在平行四边形中,是线段上一点,连结、交于点.若,则____.
15.(2023 江西)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的.“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点,,在同一水平线上,和均为直角,与相交于点.测得,,,则树高____.
16.(2023 邵阳)如图,,,点是线段上的一点,且.已知,,.
(1)证明:.
(2)求线段的长.
17.(2023 眉山)如图,中,点是的中点,连结并延长交的延长线于点.
(1)求证:;
(2)点是线段上一点,满足,交于点,若,,求的长.
18.(2023 苏州)如图,是的内接三角形,是的直径,,,点在上,连接并延长,交于点,连接,作,垂足为.
(1)求证:;
(2)若,求的长.
九.相似三角形的应用(共2小题)
19.(2023 南充)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为
A. B. C. D.
20.(2023 镇江)如图,用一个卡钳测量某个零件的内孔直径,量得长度为,则等于 ____.
十.位似变换(共5小题)
21.(2023 朝阳)如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为2,把放大,则点的对应点的坐标是
A. B.或
C. D.或
22.(2023 遂宁)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点、成位似关系,则位似中心的坐标为
A. B. C. D.
23.(2023 烟台)如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点为位似中心作正方形,正方形,,按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为,,,,则顶点的坐标为
A. B. C. D.
24.(2023 阜新)如图,和是以点为位似中心的位似图形,相似比为,则和的面积比是 ____.
25.(2023 盘锦)如图,的顶点坐标是,,,以点为位似中心,将缩小为原来的,得到△,则点的坐标为 ____.
十一.相似形综合题(共1小题)
26.(2023 福建)如图1,在中,,,是边上不与,重合的一个定点.于点,交于点.是由线段绕点顺时针旋转得到的,,的延长线相交于点.
(1)求证:;
(2)求的度数;
(3)若是的中点,如图2,求证:.
知识必备12 相似三角形
易错点:在研究三角形相似时,如果没有明确对应关系时,就一定要分类讨论,否则解答不完整.
一、解答题
1.(2024上·安徽合肥·九年级统考期末)如图,在中,,,点P从点A开始沿边向B点以的速度移动,点Q从点B开始沿边向点C以的速度移动,如果点P,Q分别从A,B同时出发,问经过几秒钟,与相似.
【答案】经过秒或秒钟,与相似.
【分析】本题考查相似三角形的性质,设经过秒钟时,与相似,得到,,,讨论对应边的不同,分别利用相似三角形对应边成比例,建立方程求解即可.
【详解】解:设经过秒钟,与相似.
由题意得,,
,,
,,
与相似,
当与对应时,有,即,解得,
当与对应时,有,即,解得,
综上所述,经过秒或秒钟,与相似.
2.(2023上·浙江杭州·九年级统考期末)四边形中,点E在边上,连结.
(1)如图1,若,证明:.
(2)如图2,若四边形为矩形,,,且与E、B、C为顶点的三角形相似,求的长.
【答案】(1)见解析
(2)或1或4
【分析】本题考查相似三角形的判定与性质、矩形的性质等知识.
(1)由点E在边上,且,得,,所以,又因为,所以根据“有两个角分别相等的两个三角形相似”即可证明;
(2)分两种情况:或,设,根据相似三角形的对应边成比例列方程求出x的值即可.
【详解】(1)证明:∵点E在边上,且,
∴,,
∴,
∵,
∴;
(2)如图2、如图3,
分两种情况:
设,
∵,
当时,
∴,
∴,
解得;
时,
∴,
∴,
解得:,
综上,或1或4.
3.(2024上·陕西宝鸡·九年级宝鸡市新建路中学校考期末)如图,在中,,,,点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动.若点、点同时出发,当某点到终点时,另一点立即停止运动.运动时间为.
(1)_________,_________;(用含的代数式表示)
(2)请计算当点运动多少秒时,以、、为顶点的三角形与相似.
【答案】(1);
(2)秒或秒
【分析】本题考查相似三角形的判定和性质,三角形的面积,
(1)根据路程=速度×时间以及线段的和差,即可列出代数式;
(2)分两种情况,或,分别得到关于的方程,求出的值,即可解决问题;
掌握相似三角形的判定和性质是解题的关键.
【详解】(1)解:∵点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动,,,
∴,,
故答案为:;;
(2)设点运动秒时,以、、为顶点的三角形与相似,
∵点从点开始沿边向点以的速度运动,点从点沿边向点以的速度运动,点、点同时出发,当某点到终点时,另一点立即停止运动,,,
∴点运动到终点所需时间为:,
点运动到终点所需时间为:,
∴的取值范围是:,
∵,
∴可分两种情况:
当时,
∴,
∴,
∴;
当时,
∴,
∴,
∴;
∴当点运动2.4秒或秒时,以、、为顶点的三角形与相似.
4.(湖南省常德市初中教学联盟校2023-2024学年九年级上学期期末数学试题)综合与实践
如图,在中,,点P以每秒2个单位长度的速度从点A出发,沿方向向终点B匀速运动,同时点Q以每秒1个单位长度的速度从点C出发,沿方向向终点A匀速运动,连接.设运动的时间为t秒.
(1)求的长(用含t的代数式表示).
(2)当秒时,求的面积.
(3)如图2,连接,当为直角三角形时,求所有满足条件t的值.
【答案】(1)
(2)9
(3)或
【分析】本题考查了勾股定理解直角三角形,相似三角形的性质与判定等知识,熟知相关知识并根据题意添加适当辅助线构造直角三角形运用勾股定理或相似三角形是解题关键,第(3)步要注意分类讨论.
(1)根据勾股定理求出,根据题意即可表示出;
(2)作,根据题意得到,,证明,求出,根据三角形面积公式即可求出;
(3)先表示出,,,,分和两种情况,分别根据勾股定理和相似三角形的判定和性质即可求解.
【详解】(1)解:在中,由勾股定理可得,
由题意可得:,则;
(2)解:如图,作,
由题意可得:,,
∵,
∴,
∵,
∴,
∴,
即,
解得,
;
(3)解:由题意可得:,,,,
①如图2,当时,根据勾股定理得,,
∴,
∴
解得:,符合题意;
②如图3,当时,作垂足为E,
由(1)得,
∴,
即,
∴,,
∴.
∵,
∴,
∴,
∴,
,
,
即,
解得,(不合题意,舍去).
∴或.
一.比例的性质(共2小题)
1.(2023 金昌)若,则
A.6 B. C.1 D.
【分析】直接利用比例的性质,内项之积等于外项之积即可得出答案.
【解答】解:,
.
故选:.
【点评】此题主要考查了比例的性质,正确将原式变形是解题关键.
2.(2023 甘孜州)若,则__1__.
【分析】根据比例的性质解答即可.
【解答】解:,
.
故答案为:1.
【点评】本题考查了比例的性质,解决本题的关键是掌握比例的性质.
二.黄金分割(共1小题)
3.(2023 广东)我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了
A.黄金分割数 B.平均数 C.众数 D.中位数
【分析】根据黄金分割的定义,即可解答.
【解答】解:我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了黄金分割数,
故选:.
【点评】本题考查了黄金分割,算术平均数,中位线,众数,统计量的选择,熟练掌握这些数学知识是解题的关键.
三.平行线分线段成比例(共3小题)
4.(2023 吉林)如图,在中,点在边上,过点作,交于点.若,,则的值是
A. B. C. D.
【分析】由,利用平行线分线段成比例,可得出,再代入,,,即可求出结论.
【解答】解:,
.
故选:.
【点评】本题考查了平行线分线段成比例,牢记“平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例”是解题的关键.
5.(2023 常州)小明按照以下步骤画线段的三等分点:
画法 图形
(1)以为端点画一条射线; (2)用圆规在射线上依次截取3条等长线段、、,连接; (3)过点、分别画的平行线,交线段于点、.、就是线段的三等分点.
这一画图过程体现的数学依据是
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
【分析】根据平行线分线段成比例定理解答即可.
【解答】解:,
,
,
,
这一画图过程体现的数学依据是两条直线被一组平行线所截,所得的对应线段成比例,
故选:.
【点评】本题考查的是平行线分线段成比例定理,尺规作图,掌握平行线分线段成比例定理是解题的关键.
6.(2023 北京)如图,直线,交于点,,若,,,则的值为 ____.
【分析】根据题意求出,再根据平行线分线段成比例定理计算即可.
【解答】解:,,
,
,
,
故答案为:.
【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
四.相似图形(共1小题)
7.(2023 泰州)两个相似图形的周长比为,则面积比为 ____.
【分析】由两个相似图形,其周长之比为,根据相似图形的周长的比等于相似比,即可求得其相似比,又由相似图形的面积的比等于相似比的平方,即可求得答案.
【解答】解:两个相似图形,其周长之比为,
其相似比为,
其面积比为.
故答案为:.
【点评】此题考查了相似图形的性质.此题比较简单,注意熟记定理是关键.
五.相似多边形的性质(共1小题)
8.(2023 威海)如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为.若矩形与原矩形相似,,则的长为
A. B. C. D.
【分析】设,根据矩形的性质可得,,再根据折叠的性质可得:,,,从而可得四边形是正方形,然后利用正方形的性质可得,最后利用相似多边形的性质,进行计算即可解答.
【解答】解:设,
四边形是矩形,
,,
由折叠得:,,,
四边形是矩形,
,
四边形是正方形,
,
矩形与原矩形相似,
,
,
解得:或,
经检验:或都是原方程的根,
,
,
,
故选:.
【点评】本题考查了相似多边形的性质,解一元二次方程公式法,矩形的性质,翻折变换(折叠问题),正方形的判定与性质熟练掌握相似多边形的性质是解题的关键.
六.相似三角形的性质(共2小题)
9.(2023 重庆)如图,已知,,若的长度为6,则的长度为
A.4 B.9 C.12 D.13.5
【分析】根据相似三角形的性质列出方程即可求解.
【解答】解:,.
,
当时,.
故选:.
【点评】本题主要考查了相似三角形的性质,找到对应的边成比例是解题的关键.
10.(2023 重庆)若两个相似三角形周长的比为,则这两个三角形对应边的比是
A. B. C. D.
【分析】根据相似三角形的性质:相似三角形周长的比等于相似比,求解即可.
【解答】解:两个相似三角形周长的比为,
这两个三角形对应边的比为,
故选:.
【点评】本题考查了相似三角形的性质,熟练掌握相似三角形的性质是解题的关键.
七.相似三角形的判定(共1小题)
11.(2023 大庆)在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为,点对应的点记为点,若点恰好落在边上,则图中与一定相似的三角形是 ____.
【分析】利用矩形的性质得到,然后利用折叠的性质推导出,进而得到,由此推断出.
【解答】解:四边形是矩形,
,
,由折叠的性质可知,,
,
,
,
故答案为:.
【点评】本题主要考查了相似三角形的判定、矩形的性质以及翻折变换(折叠问题),熟练掌握相似三角形的判定方法是解答本题的关键:两角法:有两组角对应相等的两个三角形相似.
八.相似三角形的判定与性质(共7小题)
12.(2023 雅安)如图,在中,是上一点,交于点,的延长线交的延长线于点,,,则的长为
A.4 B.6 C.8 D.10
【分析】根据平行四边形的性质得出,,,于是推出,,先求出与的比值,继而得出与的比值,再根据相似三角形对应边成比例即可求出的长.
【解答】解:四边形是平行四边形,
,,,
,
,
,
,,
,
即,
,
,
,
,
,,
,
,
,
故选:.
【点评】本题考查了平行四边形的性质和相似三角形的判定与性质,熟练掌握这些图形的性质是解题的关键.
13.(2023 哈尔滨)如图,,相交于点,,是的中点,,交于点,若,,则的长为
A.2 B.4 C.6 D.8
【分析】由易得,根据相似三角形的性质可得,于是,求出,易得为的中位线,则.
【解答】解:,
,
,
,
,
,
,
,
,
,是的中点,
为的中位线,
.
故选:.
【点评】本题主要考查相似三角形的判定与性质、三角形中位线定理,熟记“8”字模型相似三角形,以及三角形中位线定理是解题关键.
14.(2023 乐山)如图,在平行四边形中,是线段上一点,连结、交于点.若,则____.
【分析】通过证明,可得,即可求解.
【解答】解:四边形是平行四边形,
,,
,
设,则,
,
,
,
,
,
故答案为:.
【点评】本题考查了相似三角形的判定和性质,平行四边形的性质,证明三角形相似是解题的关键.
15.(2023 江西)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的.“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点,,在同一水平线上,和均为直角,与相交于点.测得,,,则树高__6__.
【分析】根据题意可知:,从而可以得到,然后代入数据计算,即可得到的长.
【解答】解:由题意可得,
,,,,
,
,
即,
解得,
树高,
故答案为:6
【点评】本题考查相似三角形的判定与性质,解答本题的关键是明确题意,利用数形结合的思想解答.
16.(2023 邵阳)如图,,,点是线段上的一点,且.已知,,.
(1)证明:.
(2)求线段的长.
【分析】(1)利用同角的余角相等得,可证明结论;
(2)根据相似三角形的性质即可求出答案.
【解答】(1)证明:,,,
,
,,
,
;
(2)解:,
,
,
.
【点评】本题主要考查了相似三角形的性质和判定,利用同角的余角相等得是解决问题的关键.
17.(2023 眉山)如图,中,点是的中点,连结并延长交的延长线于点.
(1)求证:;
(2)点是线段上一点,满足,交于点,若,,求的长.
【分析】(1)先根据证明,得,再根据平行线分线段成比例定理可得结论;
(2)先根据(1)可得:,由平行线的性质和等腰三角形的判定可得,证明,列比例式可得的长.
【解答】(1)证明:四边形是平行四边形,
,,
,,
是的中点,
,
,
,
,
,
;
(2)解:,,
,
,
四边形是平行四边形,
,
,,
,
,
,
,
,即,
.
【点评】本题考查平行四边形的性质,相似三角形的性质和判定,全等三角形的性质和判定等知识,掌握三角形全等和相似的性质和判定是解本题的关键.
18.(2023 苏州)如图,是的内接三角形,是的直径,,,点在上,连接并延长,交于点,连接,作,垂足为.
(1)求证:;
(2)若,求的长.
【分析】(1)根据圆周角定理得,进而可以证明结论;
(2)过点作,垂足为,证明,得,代入值即可解决问题.
【解答】(1)证明:为直径,
,
,
,
所对的圆周角为和,
,
;
(2)解:如图,过点作,垂足为,
,,,
,
,
,
,
,
,
,
,
,
,
,
.
【点评】本题考查圆周角定理、相似三角形的判定与性质、解直角三角形、勾股定理等知识点,解决本题的关键是得到.
九.相似三角形的应用(共2小题)
19.(2023 南充)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为
A. B. C. D.
【分析】根据镜面反射的性质,,再根据相似三角形对应边成比例列式求解即可.
【解答】解:如图:
,,
,
,
,
,
即,
,
故选:.
【点评】本题考查了相似三角形的应用.应用镜面反射的基本性质,得出三角形相似,再运用相似三角形对应边成比例即可解答.
20.(2023 镇江)如图,用一个卡钳测量某个零件的内孔直径,量得长度为,则等于 __18__.
【分析】根据相似三角形的判定和性质,可以求得的长.
【解答】解:,,
,
,
,
,
故答案为:18.
【点评】本题考查相似三角形的应用,求出的值是解答本题的关键.
十.位似变换(共5小题)
21.(2023 朝阳)如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为2,把放大,则点的对应点的坐标是
A. B.或
C. D.或
【分析】根据位似变换的性质计算,得到答案.
【解答】解:以原点为位似中心,相似比为2,把放大,点的坐标为,
点的对应点的坐标为或,,即或,
故选:.
【点评】本题考查的是位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或.
22.(2023 遂宁)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点、成位似关系,则位似中心的坐标为
A. B. C. D.
【分析】根据位似中心的定义作答.
【解答】解:如图:
与的对应顶点的连线相交于点,则位似中心的坐标为.
故选:.
【点评】本题主要考查了位似变换,坐标与图形性质,解题的关键是掌握“位似中心”的确定方法.
23.(2023 烟台)如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点为位似中心作正方形,正方形,,按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为,,,,则顶点的坐标为
A. B. C. D.
【分析】根据位似变换的概念、点的坐标的变化情况找出点的横纵坐标的变化规律,根据规律解答即可.
【解答】解:由题意可知:点,点,点,
,,,,,,,,,,,
顶点的坐标为,即,
故选:.
【点评】本题考查的是位似变换、点的坐标的变化规律,根据点的坐标的变化情况正确找出规律是解题的关键.
24.(2023 阜新)如图,和是以点为位似中心的位似图形,相似比为,则和的面积比是 ____.
【分析】先利用位似的性质得到,相似比为,然后根据相似三角形的性质解决问题.
【解答】解:与是以点为位似中心的位似图形,位似比为,
,相似比为,
与的面积之比为.
故答案为:.
【点评】本题考查的是位似变换的概念和性质、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.
25.(2023 盘锦)如图,的顶点坐标是,,,以点为位似中心,将缩小为原来的,得到△,则点的坐标为 __,或,__.
【分析】根据位似变换的性质计算,得到答案.
【解答】解:以原点为位似中心,把缩小为原来的,可以得到△,点的坐标为,
点的坐标是,或,,即,或,.
故答案为:,或,.
【点评】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或.
十一.相似形综合题(共1小题)
26.(2023 福建)如图1,在中,,,是边上不与,重合的一个定点.于点,交于点.是由线段绕点顺时针旋转得到的,,的延长线相交于点.
(1)求证:;
(2)求的度数;
(3)若是的中点,如图2,求证:.
【分析】(1)由是由线段绕点顺时针旋转 得到的,得,,,又,,可得,根据,有,故;
(2)设与的交点为,由,,有,,即,可得,即得,从而;
(3)延长交于点,连接,,由,知,,而是的中点,有,可得,从而,,可证,,得,,即可得,故.
【解答】(1)证明:如图:
是由线段绕点顺时针旋转 得到的,
,,,
,,
.
,
,
,
,
,
;
(2)解:设与的交点为,如图:
,,
,
,即,
,
,
,
,
,
,
;
(3)证明:延长交于点,连接,,如图:
,
,
.
是的中点,
,
,
,
,,
,,,
,
,
由(2)知,,
.
,
,
,,
,即,
,
,
.
【点评】本题考查相似三角形综合应用,涉及三角形内角和定理、平行线的判定与性质、全等三角形的判定与性质、等腰三角形及直角三角形的判定与性质等基础知识,解题的关键是掌握相似三角形的判定与性质定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
