10.2等腰三角形--反证法

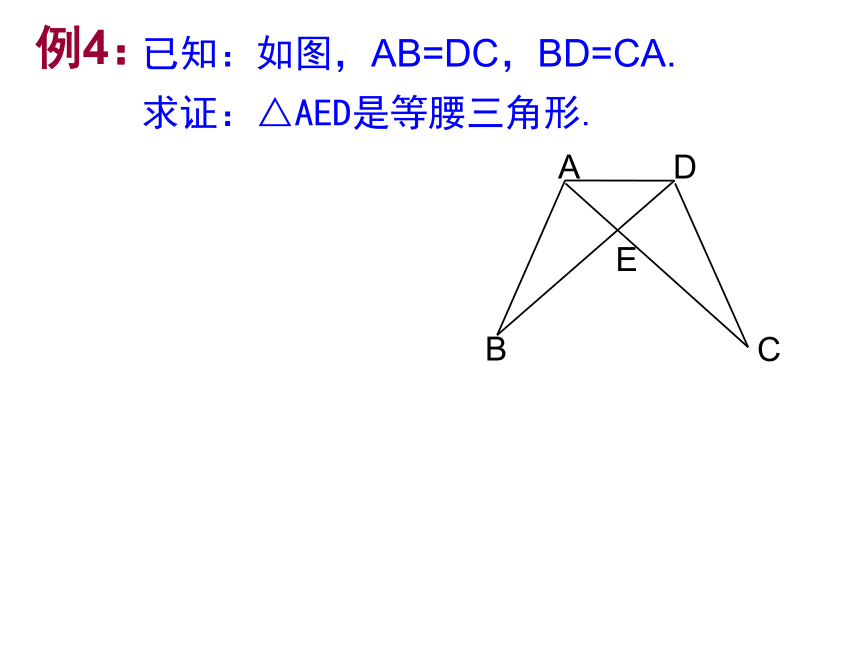
课件14张PPT。10.2等腰三角形（4）第十章 三角形的有关证明例4：已知：如图，AB=DC，BD=CA.
求证：△AED是等腰三角形. 从前有个聪明的孩子叫王戎。他7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么，
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的呢?
他运用了怎样的推理方法?小故事:路边苦李假设“李子甜”树在道边则李子少与已知条件“树在道边而多子”产生矛盾假设 “李子甜”不成立所以“树在道边而多子,此必为苦李” 是正确的王戎推理方法是:反证法教学 目 标1、了解反证法的概念及其基本步骤，并会用反证法证明简单的命题。
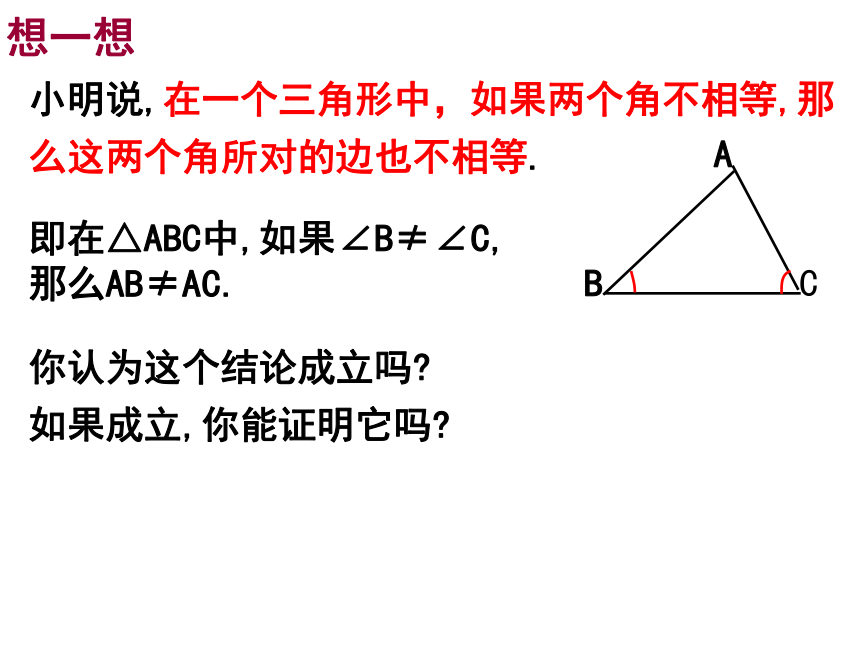
2、通过利用反证法证明命题，体会逆向思维。小明说,在一个三角形中，如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?
如果成立,你能证明它吗?即在△ABC中,如果∠B≠∠C,
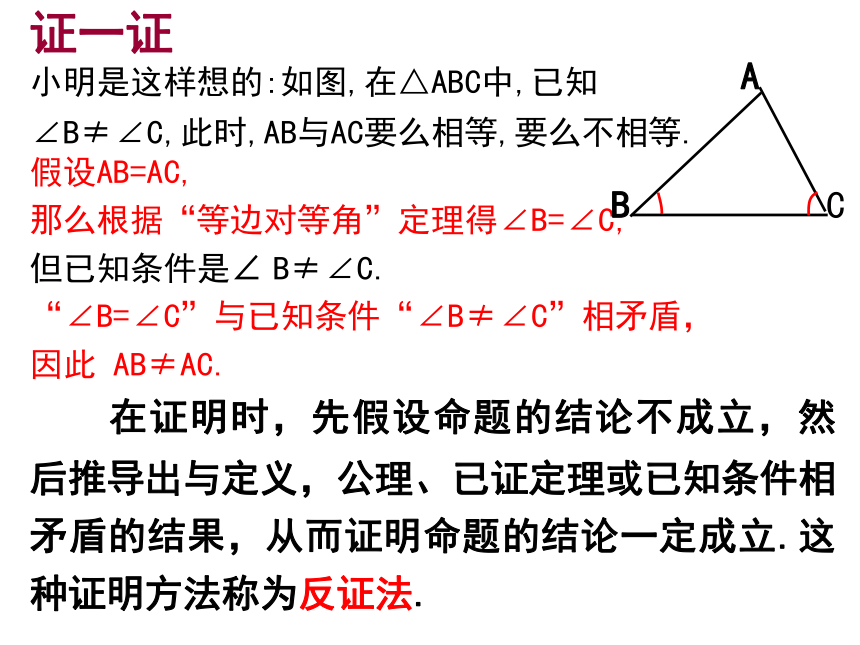
那么AB≠AC.想一想小明是这样想的:如图,在△ABC中,已知∠B≠∠C,此时,AB与AC要么相等,要么不相等.假设AB=AC,
那么根据“等边对等角”定理得∠B=∠C,
但已知条件是∠ B≠∠C.
“∠B=∠C”与已知条件“∠B≠∠C”相矛盾，
因此 AB≠AC.证一证 在证明时，先假设命题的结论不成立，然后推导出与定义，公理、已证定理或已知条件相矛盾的结果，从而证明命题的结论一定成立.这种证明方法称为反证法.1.提出假设:先假设命题的结论不成立;即结论的反面成立;
2.推出矛盾:从这个假设出发,应用正确的推论方法,得出与定义，公理、已证定理或已知条件相矛盾的结果;
3.肯定结论:由矛盾的结果判定假设不正确,从而肯定命题的结论正确.反证法的一般步骤:　 用反证法证明（填空）：在三角形的内角中，至少有一个角大于或等于６０°已知：如图， ∠Ａ，∠Ｂ，∠Ｃ是△ＡＢＣ的内角。求证： ∠Ａ，∠Ｂ，∠Ｃ中至少有一个角大于或等于６０度。证明：假设所求证的结论不成立，即
∠Ａ＿＿６０°， ∠Ｂ＿＿６０°，∠Ｃ＿＿６０°
则　∠Ａ＋∠Ｂ＋∠Ｃ　＜　１８０度
这与＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿相矛盾。
所以假设命题＿＿＿＿＿＿，
因此， ∠Ａ，∠Ｂ，∠Ｃ中至少有
一个角大于或等于６０度．＜＜＜三角形的内角和等于１８０°不成立试试看!已知a1、a2、a3、a4、a5都是正数，且a1+a2+a3+a4+a5=1，那么这五个数中至少有一个大于或等于1/5.试一试 如何证明这个结论？用反证法来证:
证明: 假设这五个数中没有一个大于或等于1/5,
即都不得小于1/5,
那么这五个数的和a1+a2+a3+a4+a5就小于1.
这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.
因此,假设不成立，即这五个数中至少有一个大于或等于1/5成立.已知，在△ABC中,求证∠A、∠B、∠C这三个角中，至少有两个锐角.你能用反证法证明以下命题吗？延伸拓展证明：假设△ABC的三个内角中至多有一个锐角,
则这三个角中，至少有两个直角或钝角.这与三角形的三个内角和等于180°相矛盾；不妨设900≤∠B＜1800,900≤∠C＜1800,
则∠A+∠B+∠C＞1800.因此,假设不成立，三角形中至少有两个锐角.作业：109页：随堂练习
当堂达标见导学案课堂小结1. 知识方面: ______________________________

2.数学思想方法方面:_________________________-