2.3简单的轴对称图形课件(13张ppt)
文档属性
| 名称 | 2.3简单的轴对称图形课件(13张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 86.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-04 00:00:00 | ||
图片预览



文档简介
课件13张PPT。角是轴对称图形吗?2.3简单的轴对称图形2学习目标1.了解角的对称轴并会画出图形;
2.探索角的平分线的性质;
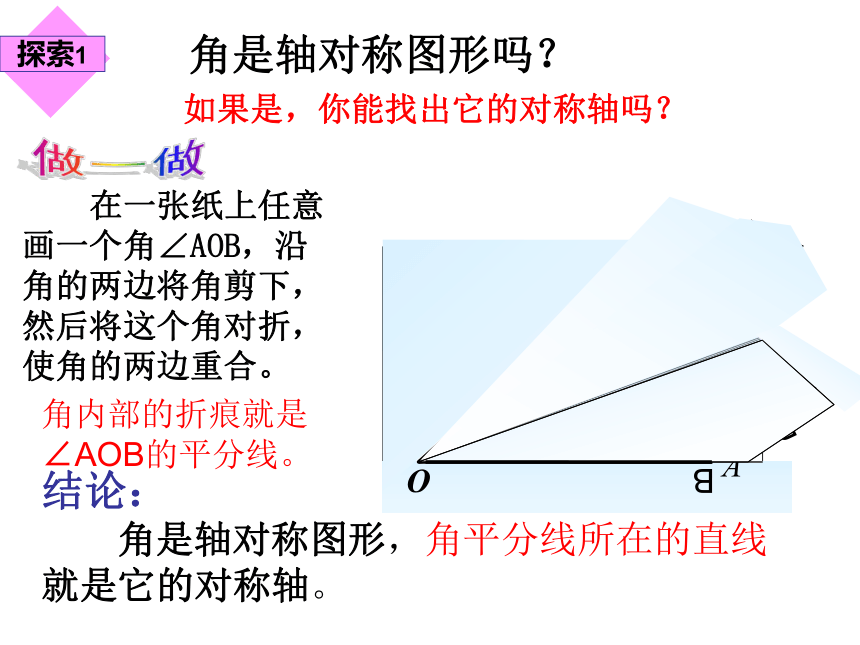
3.能用尺规作已知角的平分线。AOB角是轴对称图形吗?如果是,你能找出它的对称轴吗? 在一张纸上任意画一个角∠AOB,沿角的两边将角剪下,然后将这个角对折,使角的两边重合。做一做结论:
角是轴对称图形,角平分线所在的直线
就是它的对称轴。角内部的折痕就是
∠AOB的平分线。 新的折痕与OB
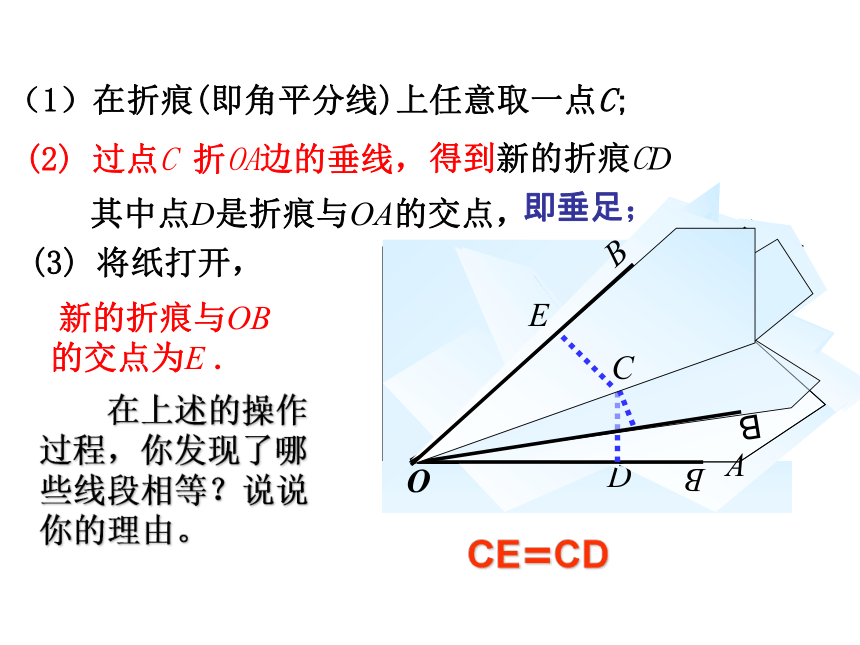
的交点为E .AOB(2) 过点C 折OA边的垂线,得到新的折痕CD,(3) 将纸打开,E 其中点D是折痕与OA的交点,即垂足;(1)在折痕(即角平分线)上任意取一点C; 在上述的操作过程,你发现了哪些线段相等?说说你的理由。CE=CDAOBCE=CDE在折痕上另取一点,
再试一试。角平分线的性质:
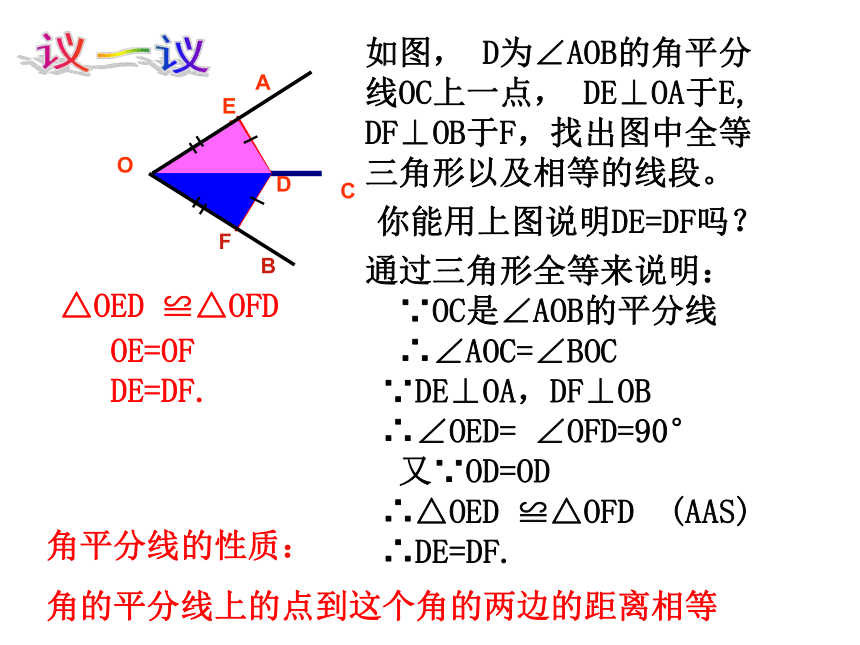
角的平分线上的点到这个角的两边的距离相等CDEF如图, D为∠AOB的角平分线OC上一点, DE⊥OA于E, DF⊥OB于F,找出图中全等三角形以及相等的线段。议一议你能用上图说明DE=DF吗?通过三角形全等来说明:
∵OC是∠AOB的平分线
∴∠AOC=∠BOC
∵DE⊥OA,DF⊥OB
∴∠OED= ∠OFD=90°
又∵OD=OD
∴△OED ≌△OFD (AAS)
∴DE=DF.△OED ≌△OFDOE=OF
DE=DF.角平分线的性质:
角的平分线上的点到这个角的两边的距离相等(1)∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。BD CD(×)判断:(2)∵ 如图, DC⊥AC,DB⊥AB (已知) BD CD∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。(×)(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。(√)不必再证全等用尺规作角的平分线的方法AB作法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.3.作射线OC.则射线OC就是∠AOB的平分线. ⒈如图,在Rt△ABC中,∠C=90°,BD 是∠B的平分线,DE⊥AB,垂足为E,DE与DC相等吗?说明理由。分析:
因为BD是∠ABC的平分线;
在Rt△ABC中, ∠C=90°,
所以DC⊥BC
又因为DE⊥AB
所以DE=DC开拓创新 试一试有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD与角的两边重合,沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?回味无穷◆这节课我们学习了哪些知识? 1、角的平分线的性质: 角的平分线上的点到角的两边的距离相等。几何语言:∵ OC是∠AOB的平分线,
又 PD⊥OA,PE⊥OB
∴ PD=PE(角的平分线上的点
到角的两边距离相等). 2、“作已知角的平分线”的尺规作图;当堂达标见导学案作 业: 课本P50习题2.4:1、2。
2.探索角的平分线的性质;
3.能用尺规作已知角的平分线。AOB角是轴对称图形吗?如果是,你能找出它的对称轴吗? 在一张纸上任意画一个角∠AOB,沿角的两边将角剪下,然后将这个角对折,使角的两边重合。做一做结论:
角是轴对称图形,角平分线所在的直线
就是它的对称轴。角内部的折痕就是
∠AOB的平分线。 新的折痕与OB
的交点为E .AOB(2) 过点C 折OA边的垂线,得到新的折痕CD,(3) 将纸打开,E 其中点D是折痕与OA的交点,即垂足;(1)在折痕(即角平分线)上任意取一点C; 在上述的操作过程,你发现了哪些线段相等?说说你的理由。CE=CDAOBCE=CDE在折痕上另取一点,
再试一试。角平分线的性质:
角的平分线上的点到这个角的两边的距离相等CDEF如图, D为∠AOB的角平分线OC上一点, DE⊥OA于E, DF⊥OB于F,找出图中全等三角形以及相等的线段。议一议你能用上图说明DE=DF吗?通过三角形全等来说明:
∵OC是∠AOB的平分线
∴∠AOC=∠BOC
∵DE⊥OA,DF⊥OB
∴∠OED= ∠OFD=90°
又∵OD=OD
∴△OED ≌△OFD (AAS)
∴DE=DF.△OED ≌△OFDOE=OF
DE=DF.角平分线的性质:
角的平分线上的点到这个角的两边的距离相等(1)∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。BD CD(×)判断:(2)∵ 如图, DC⊥AC,DB⊥AB (已知) BD CD∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。(×)(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。(√)不必再证全等用尺规作角的平分线的方法AB作法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.3.作射线OC.则射线OC就是∠AOB的平分线. ⒈如图,在Rt△ABC中,∠C=90°,BD 是∠B的平分线,DE⊥AB,垂足为E,DE与DC相等吗?说明理由。分析:
因为BD是∠ABC的平分线;
在Rt△ABC中, ∠C=90°,
所以DC⊥BC
又因为DE⊥AB
所以DE=DC开拓创新 试一试有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD与角的两边重合,沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?回味无穷◆这节课我们学习了哪些知识? 1、角的平分线的性质: 角的平分线上的点到角的两边的距离相等。几何语言:∵ OC是∠AOB的平分线,
又 PD⊥OA,PE⊥OB
∴ PD=PE(角的平分线上的点
到角的两边距离相等). 2、“作已知角的平分线”的尺规作图;当堂达标见导学案作 业: 课本P50习题2.4:1、2。
