期末评估测试卷A (含答案)2024-2025学年数学北师版七年级下册
文档属性
| 名称 | 期末评估测试卷A (含答案)2024-2025学年数学北师版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 690.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 20:47:19 | ||
图片预览




文档简介
期末评估测试卷A
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024赤峰中考)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
2.芯片是信息世界的基础核心,传统晶体管因接近物理极限而制约了芯片的进一步发展。北京大学研究团队成功构筑了0.000 000 01 m超短沟道弹道二维硒化铟晶体管,成为国际上迄今速度最快、能耗最低的二维晶体管,将数据0.000 000 01 m用科学记数法表示为( )
A.1×10-8 m B.1×10-9 m
C.0.1×10-8 m D.0.1×10-9 m
3.下列事件是必然事件的是( )
A.抛出的篮球不会下落
B.射击运动员射击一次,命中10环
C.早晨太阳从东方升起
D.任意掷一枚硬币,落地后正面向上
4.(2024云南中考)下列计算正确的是( )
A.x3+5x3=6x4 B.x6÷x3=x5
C.(a2)3=a7 D.(ab)3=a3b3
5.(2024南充中考)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A.80° B.90° C.100° D.120°
6.下列各式能用平方差公式计算的是( )
A.(2x-y)(x+2y) B.(x-y)(y-x)
C.(b+a)(b-c) D.(-a+b)(a+b)
7.(2024盐城中考)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
A.25° B.35° C.45° D.55°
8.如图,△AOB≌△OCD,∠B=∠D=90°,下列结论错误的是( )
A.∠AOB=∠C B.∠A+∠C=90°
C.AO⊥CO D.AO=CD
9.下面三个问题中都有两个变量:①如图1,货车匀速通过隧道(隧道长大于货车长),货车在隧道内的长度y与从车头进入隧道至车尾离开隧道的时间x;②如图2,实线是王大爷从家出发匀速散步行走的路线(圆心O表示王大爷家的位置),他离家的距离y与散步的时间x;③如图3,往空杯中匀速倒水,倒满后停止,一段时间后,再匀速倒出杯中的水,杯中水的体积y与所用时间x。
其中,变量y与x之间的关系大致符合下图的是( )
A.①② B.①③ C.②③ D.①②③
10.如图,已知△ABC,按如下步骤作图:①分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点E和F;②作直线EF,分别交AB,BC于点M,N;③连接AN。若AM=2,△ACN的周长为12,则△ABC的周长为( )
A.16 B.15 C.14 D.13
二、填空题(本题共5小题,每小题3分,共15分)
11.计算3-1的结果是________。
12.北普陀山是锦州著名的景点之一,五一期间,某中学组织20名教师和x名学生到北普陀山开展活动,已知成人票每张50元,学生票每张25元,若设门票的总费用为y元,则y与x之间的关系式为________。
13.(2024泸州中考)在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同。若从中随机摸出一个球是白球的概率是,则黄球的个数为________。
14.如图,点E,F在线段AC上(不与点A,C重合),△ADF≌△CBE,若AC=8,EF=2,则AE的长为________。
15.如图,△APB与△CPD均是等腰三角形,且∠APB=∠CPD=90°,连接AC,AD,BC,BD,AP=3,CP=2,在△CPD绕点P旋转的过程中,四边形ABCD面积的最大值为________。
三、解答题(本题共8小题,共75分。解答应写出文字说明、演算步骤或推理过程)
16.(8分)(1)计算:xy·(-2xy2)2÷x2y4。
(2)先化简,再求值:[(a-2b)2+(a-b)·(a+4b)]÷2a,其中a=-1,b=2。
17.(8分)某商场促销,顾客当日消费即可参与一次转盘抽奖,如图,转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时无效,需要重转),若指计指向的数字为4的倍数则可以领取一份奖品,请计算顾客获奖的概率。
18.(8分)在弹性限度内,弹簧的长度随所挂物体质量的增加而伸长,经过实验发现,弹簧的长度y(cm)与所挂物体质量x(kg)之间的对应关系如下表:
所挂物体质量x/kg 0 1 2 3 4 …
弹簧的长度y/cm 12 12.5 13 13.5 14 …
(1)在这个变化过程中,自变量和因变量各是什么?
(2)请根据表格中的数据,求挂物体后弹簧的长度y(cm)与所挂物体质量x(kg)之间的关系式。
(3)在弹性限度内,弹簧伸长后的最大长度为20 cm,该弹簧最多能挂多重的物体?
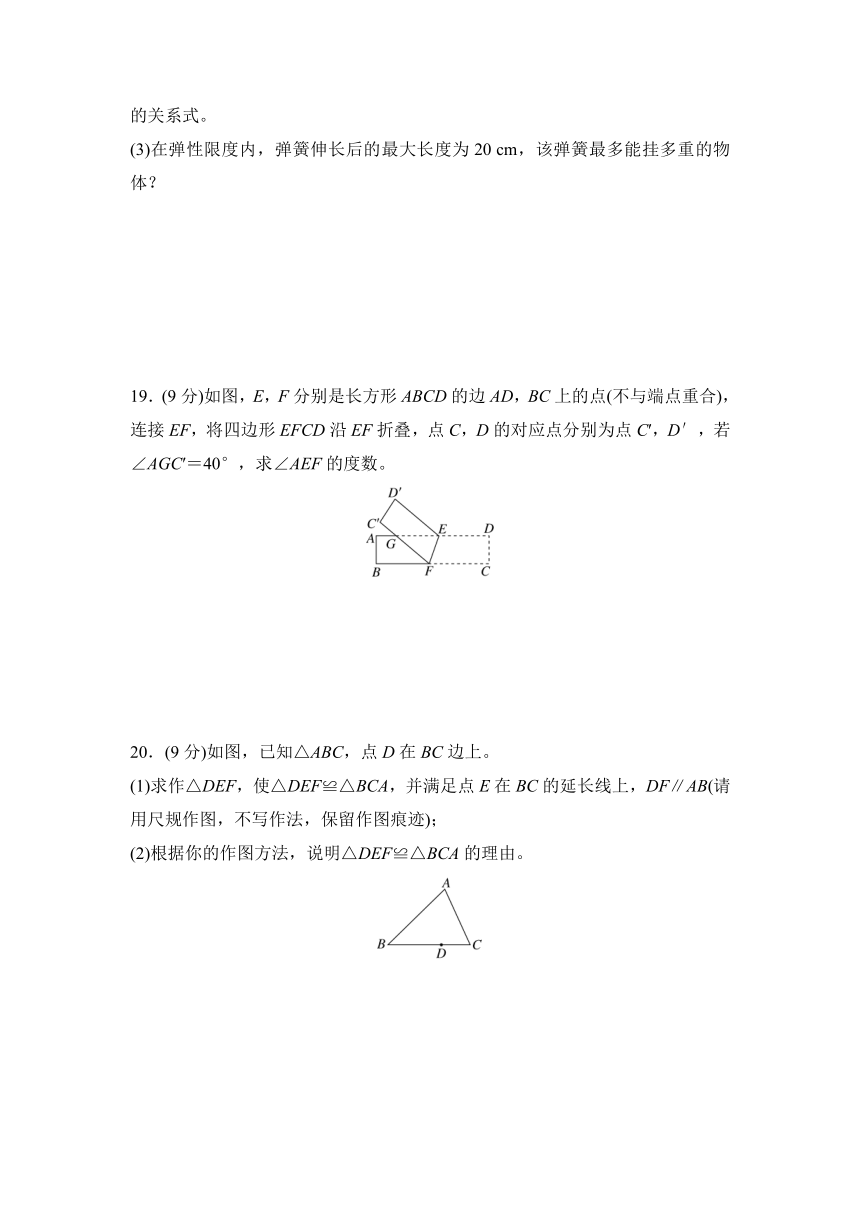
19.(9分)如图,E,F分别是长方形ABCD的边AD,BC上的点(不与端点重合),连接EF,将四边形EFCD沿EF折叠,点C,D的对应点分别为点C′,D′,若∠AGC′=40°,求∠AEF的度数。
20.(9分)如图,已知△ABC,点D在BC边上。
(1)求作△DEF,使△DEF≌△BCA,并满足点E在BC的延长线上,DF∥AB(请用尺规作图,不写作法,保留作图痕迹);
(2)根据你的作图方法,说明△DEF≌△BCA的理由。
21.(10分)2024年6月2日,锦州迎来了一场体育盛宴——“跑遍辽宁”“奔赴山海前程‘是’锦”2024锦州马拉松赛。这场全民参与的体育盛宴在风景如画的滨河路凌川大桥下拉开帷幕。甲、乙两名选手均参加了10 km健康跑项目(5 km处折返),他们同时出发,两选手所跑的路程y(km)与时间x(min)之间的关系如图所示,请根据图象回答下列问题:
(1)求甲选手前4 km的平均速度。
(2)乙选手追上甲选手时,他们距离终点还有多少千米?
(3)若甲选手跑最后一段的平均速度与他前4 km的平均速度相同,那么当乙选手到达终点时,甲选手还要经过多长时间到达终点?
22.(11分)【方法回顾】
在学习整式的乘法时,我们曾用两种不同的方法,表示同一个长方形的面积,进而得到单项式与多项式相乘的法则,也曾经用两种不同的方法,表示同一个正方形的面积来验证和解释乘法公式,我们将这种方法称为“等积法”。它的基本思想是:将同一个量从两个不同角度计算两次,我们常用“等积法”列出等量关系、求线段长度或线段之间的数量关系。
【方法应用】
(1)如图1,正方形ABCD是由长为a、宽为b的4个全等的小长方形拼摆而成的,我们可以利用该正方形面积的不同表示方法验证一个与完全平方公式相关的等量关系,请你写出这个等量关系。
【方法迁移】
(2)如图2,长方形ABCD是由8个长为a、宽为b的全等的小长方形拼摆而成的,请你根据“等积法”计算两次的基本思想,解答下列问题:
①求a,b之间的数量关系;
②若长方形ABCD的宽AB=40 cm,求小长方形的面积。
【拓展应用】
(3)如图3,在△ABC中,∠ABC=90°,AB=6,BC=8,AC=10,P是△ABC三条角平分线的交点,求点P到边AC的距离。
23.(12分)【问题提出】
期末复习课上,数学丁老师出示了下面一个问题:如图1,在△ABC中,D是BA延长线的点,E是AC边上一点,且满足DE=BC,∠DEA=∠ACB,那么A是BD的中点。请你说明理由。
【思路探究】
小王同学从条件出发分析解题思路:以DE为腰构造等腰三角形DEF和平行八字型全等三角形,如图2,以点D为圆心,以DE长为半径画弧,交CA的延长线于点F,先应用等腰三角形的轴对称性,再应用三角形全等“AAS”(或“ASA”)的判定方法即可得AB=AD;
小张同学从结论出发分析解题思路:以AB为腰构造等腰三角形ABF,将说明AD=AB的问题转化为说明AD=BF的问题,如图3,以点B为圆心,以AB长为半径画弧,交AC于点F,于是可得∠BFA=∠BAF,再应用三角形全等“AAS”(或“ASA”)的判定方法即可得AB=BF=AD。
(1)请你选择小王同学或小张同学的思路或按自己的思路写出完整的解题过程。
【学以致用】
(2)请你在理解了小张同学或小王同学解题思路的基础上,解答下面一道图形较为复杂的同类问题:如图4,在四边形ABCD中,AB=AC=CD,∠ACD=90°,过点B作线段BE⊥AB,且BE=AB,连接DE,交BC的延长线于点F,猜想DF与EF的数量关系并说明理由。
【详解答案】
1.A 解析:A.是轴对称图形,故本选项符合题意;B.不是轴对称图形,故本选项不合题意;C.不是轴对称图形,故本选项不合题意;D.不是轴对称图形,故本选项不合题意。故选A。
2.A 解析:0.000 000 01 m=1×10-8 m。故选A。
3.C 解析:A.抛出的篮球不会下落,是不可能事件,故本选项不符合题意;B.射击运动员射击一次,命中10环是随机事件,故本选项不符合题意;C.早晨太阳从东方升起,是必然事件,故本选项符合题意;D.任意掷一枚硬币,落地后正面向上,是随机事件,故本选项不符合题意。故选C。
4.D 解析:A.x3+5x3=6x3,故A选项错误;B.x6÷x3=x3,故B选项错误;C.(a2)3=a6,故C选项错误;D.(ab)3=a3b3,故D选项正确。故选D。
5.C 解析:如图。因为∠1=∠2=40°,
所以∠4=180°-∠1-∠2=100°。因为两个平面镜平行放置,所以经过两次反射后的光线与入射光线平行,所以∠3=∠4=100°。故选C。
6.D 解析:A.(2x-y)(x+2y)不能用平方差公式计算,故本选项不符合题意;B.(x-y)(y-x)不能用平方差公式计算,故本选项不符合题意;C.(b+a)(b-c)不能用平方差公式计算,故本选项不符合题意;D.(-a+b)(a+b)能用平方差公式计算,故本选项符合题意。故选D。
7.B 解析:如图:
因为直尺的两边平行,∠1=55°,所以∠ABC=∠1=55°,∠ACB=∠2。因为∠BAC=90°,所以∠ACB=180°-∠BAC-∠ABC=180°-90°-55°=35°,所以∠2=∠ACB=35°。故选B。
8.D 解析:因为△AOB≌△OCD,所以∠AOB=∠C,故A选项正确;因为△AOB中,∠B=90°,所以∠A+∠AOB=90°。因为∠AOB=∠C,所以∠A+∠C=90°,故B选项正确;因为△OCD中,∠D=90°,所以∠COD+∠C=90°。因为∠AOB=∠C,所以∠COD+∠AOB=90°,所以∠AOC=90°,所以AO⊥CO,故C选项正确;因为△AOB≌△OCD,所以AO=CO,所以AO≠CD,故D选项错误。故选D。
9.D 解析:①当货车开始进入隧道时,y逐渐变大;当货车完全进入隧道,由于隧道长大于货车长,此时y不变且最大;当货车开始离开隧道时,y逐渐变小。故①正确。②王大爷离家的距离y先逐渐变大,他走的是一段弧线时,此时y不变且最大,之后逐渐离家越来越近直至回家,即y逐渐变小,故②正确。③往空杯中匀速倒水,倒满后停止,水的体积逐渐增加,一段时间后,再匀速倒出杯中的水,这期间,水的体积先保持不变,然后逐渐减少,杯中水的体积y与所用时间x之间的关系符合图象,故③正确。故选D。
10.A 解析:根据作图可知MN为AB的垂直平分线,所以AB=2AM=2BM=4,AN=BN。因为C△ACN=AN+CN+AC=12,所以BN+CN+AC=12,所以C△ABC=AB+BN+CN+AC=4+12=16。故选A。
11. 解析:3-1=。
12.y=25x+1 000 解析:依等量关系式“总费用=老师费用+学生费用”可得y=20×50+25x=25x+1 000。
13.3 解析:设黄球的个数为x,根据题意得==,所以6+x=9,解得x=3。
所以黄球的个数为3。
14.3 解析:因为△ADF≌△CBE,所以AF=CE,所以AF-EF=CE-EF,即AE=CF。因为2AE=AC-EF=8-2=6,所以AE=3。
15. 解析:如图,设AC,BD交于点J,BD,PC交于点O。
因为∠APB=∠CPD=90°,所以∠APC=∠BPD。因为PA=PB,PC=PD,所以△APC≌△BPD(SAS),所以AC=BD,∠ACP=∠BDP。因为∠POD=∠COJ,所以∠CJO=∠OPD=90°,所以AC⊥BD,所以四边形ABCD的面积=·AC2。因为AC≤PA+PC=5,所以四边形ABCD面积的最大值为。
16.解:(1)原式=xy·4x2y4÷x2y4=x3y5÷x2y4=xy。
(2)原式=(a2-4ab+4b2+a2+4ab-ab-4b2)÷2a
=(2a2-ab)÷2a
=a-b。
当a=-1,b=2时,
原式=-1-1=-2。
17.解:由题意可知,任意转动一次转盘,指针指向的数字共有12种可能的结果,因为转盘是12等份,所以每种结果出现的可能性相同,其中指针指向数字是4的倍数的结果有3种,分别是4,8,12。
所以P(顾客获奖)==。
18.解:(1)自变量是所挂物体质量,因变量是弹簧的长度。
(2)由表格数据可知,x每增加1 kg,y就增加0.5 cm,
所以挂物体后弹簧的长度y与所挂物体的质量x之间的关系式为y=12+0.5x。
(3)令y=20,则12+0.5x=20,
解得x=16,
所以该弹簧最多能挂16 kg的物体。
19.解:因为长方形ABCD,
所以AD∥BC,所以∠BFG=∠AGC′=40°,∠AEF=∠EFC,
所以∠CFG=180°-∠BFG=140°。
由折叠性质可知∠GFE=∠EFC=∠CFG,
所以∠EFC=×140°=70°,
所以∠AEF=70°。
20.解:(1)如图所示即为所求。
(2)根据作图得DF=AB,∠FDE=∠B,DE=BC,
所以△DEF≌△BCA(SAS)。
21.解:(1)根据题图可知,v甲=4÷10=(km/min)。
答:甲选手前4 km的平均速度为 km/min。
(2)由题图可知,v乙=10÷50=(km/min),
乙选手追上甲选手时,他们距离终点的路程s=×(50-30)=4(km)。
答:乙选手追上甲选手时,他们距离终点还有4 km。
(3)由题图可知,甲最后的冲刺阶段距离终点还有10-8=2(km),
所以t甲=2÷=5(min)。
答:乙选手到达终点时,甲选手还要经过5 min到达终点。
22.解:(1)大正方形的边长为(a+b),面积为(a+b)2;小正方形的边长为(a-b),面积为(a-b)2;4个长方形的面积之和为4ab,所以(a+b)2=(a-b)2+4ab。
(2)①因为长方形ABCD的面积为2a·(a+b),小长方形的面积为ab,
所以2a·(a+b)=8ab,即2a2+2ab=8ab,所以2a2-6ab=0,即a2-3ab=0。
因为a≠0,所以a2=3ab,所以a=3b。
②因为AB=40 cm,所以a+b=40 cm,
所以3b+b=40 cm,
解得b=10 cm,所以a=3b=30 cm,
所以小长方形的面积为ab=30×10=300(cm2)。
(3)设点P到边AC的距离为h。
因为点P是△ABC三条角平分线的交点,
所以点P到边AB的距离,到边BC的距离都等于点P到边AC的距离,
即点P到边AB的距离为h,到边BC的距离为h。
因为在△ABC中,∠ABC=90°,AB=6,BC=8,
所以S△ABC=×6×8=24。
因为S△ABC=S△PAC+S△PBC+S△PAB
=AC·h+BC·h+AB·h,
=×10h+×8h+×6h
=12h,
所以12h=24,解得h=2,即点P到边AC的距离为2。
23.解:(1)小王同学的思路:
如题图2,以点D为圆心,以DE长为半径画弧,交CA的延长线于点F,则DF=DE。
所以∠F=∠DEA。
因为∠DEA=∠ACB,DE=BC,
所以∠F=∠ACB,DF=BC。
因为∠DAF=∠BAC,
所以△DAF≌△BAC(AAS),
所以AD=AB,即A是BD的中点。
小张同学的思路:
如题图3,以点B为圆心,以AB长为半径画弧,交AC于点F,连接BF,则BF=AB,
所以∠BAF=∠AFB。
因为∠DAE=180°-∠BAF,∠BFC=180°-∠AFB,
所以∠DAE=∠BFC。
因为∠DEA=∠ACB,DE=BC,
所以△DEA≌△BCF(AAS),所以AD=BF,
所以AB=AD,即A是BD的中点。
(答案不唯一)
(2)猜想DF=EF。理由:
方法1:如图1,以点D为圆心,CD长为半径作弧,交BF的延长线于点M,连接DM,
图1
则DM=DC,所以∠M=∠DCM。
因为AB=AC=CD=DM,∠ACD=90°,EB=BA,EB⊥BA,
所以DM=BE,∠ABC=∠ACB,∠ACB+∠DCM=90°,∠ABE=90°,
所以∠ABC+∠EBF=90°,
所以∠M=∠DCM=∠EBF。
又因为∠DFM=∠EFB,所以△DFM≌△EFB(AAS),所以DF=EF。
方法2:如图2,以点E为圆心,以EF长为半径画弧,交BF于点N,连接EN,则EN=EF,所以∠EFN=∠ENF。
因为∠CFD=180°-∠EFN,∠BNE=180°-∠ENF,所以∠CFD=∠BNE。
因为AB=AC,∠ACD=90°,EB⊥BA,
所以∠ABC=∠ACB,∠ACB+∠DCF=90°,∠ABE=90°,
图2
所以∠ABC+∠EBF=90°,
所以∠DCF=∠EBF。
因为AB=CD=BE,
所以△DCF≌△EBN(AAS),所以DF=EN,所以DF=EF。
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024赤峰中考)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
2.芯片是信息世界的基础核心,传统晶体管因接近物理极限而制约了芯片的进一步发展。北京大学研究团队成功构筑了0.000 000 01 m超短沟道弹道二维硒化铟晶体管,成为国际上迄今速度最快、能耗最低的二维晶体管,将数据0.000 000 01 m用科学记数法表示为( )
A.1×10-8 m B.1×10-9 m
C.0.1×10-8 m D.0.1×10-9 m
3.下列事件是必然事件的是( )
A.抛出的篮球不会下落
B.射击运动员射击一次,命中10环
C.早晨太阳从东方升起
D.任意掷一枚硬币,落地后正面向上
4.(2024云南中考)下列计算正确的是( )
A.x3+5x3=6x4 B.x6÷x3=x5
C.(a2)3=a7 D.(ab)3=a3b3
5.(2024南充中考)如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40°,则∠3的度数为( )
A.80° B.90° C.100° D.120°
6.下列各式能用平方差公式计算的是( )
A.(2x-y)(x+2y) B.(x-y)(y-x)
C.(b+a)(b-c) D.(-a+b)(a+b)
7.(2024盐城中考)小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
A.25° B.35° C.45° D.55°
8.如图,△AOB≌△OCD,∠B=∠D=90°,下列结论错误的是( )
A.∠AOB=∠C B.∠A+∠C=90°
C.AO⊥CO D.AO=CD
9.下面三个问题中都有两个变量:①如图1,货车匀速通过隧道(隧道长大于货车长),货车在隧道内的长度y与从车头进入隧道至车尾离开隧道的时间x;②如图2,实线是王大爷从家出发匀速散步行走的路线(圆心O表示王大爷家的位置),他离家的距离y与散步的时间x;③如图3,往空杯中匀速倒水,倒满后停止,一段时间后,再匀速倒出杯中的水,杯中水的体积y与所用时间x。
其中,变量y与x之间的关系大致符合下图的是( )
A.①② B.①③ C.②③ D.①②③
10.如图,已知△ABC,按如下步骤作图:①分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点E和F;②作直线EF,分别交AB,BC于点M,N;③连接AN。若AM=2,△ACN的周长为12,则△ABC的周长为( )
A.16 B.15 C.14 D.13
二、填空题(本题共5小题,每小题3分,共15分)
11.计算3-1的结果是________。
12.北普陀山是锦州著名的景点之一,五一期间,某中学组织20名教师和x名学生到北普陀山开展活动,已知成人票每张50元,学生票每张25元,若设门票的总费用为y元,则y与x之间的关系式为________。
13.(2024泸州中考)在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同。若从中随机摸出一个球是白球的概率是,则黄球的个数为________。
14.如图,点E,F在线段AC上(不与点A,C重合),△ADF≌△CBE,若AC=8,EF=2,则AE的长为________。
15.如图,△APB与△CPD均是等腰三角形,且∠APB=∠CPD=90°,连接AC,AD,BC,BD,AP=3,CP=2,在△CPD绕点P旋转的过程中,四边形ABCD面积的最大值为________。
三、解答题(本题共8小题,共75分。解答应写出文字说明、演算步骤或推理过程)
16.(8分)(1)计算:xy·(-2xy2)2÷x2y4。
(2)先化简,再求值:[(a-2b)2+(a-b)·(a+4b)]÷2a,其中a=-1,b=2。
17.(8分)某商场促销,顾客当日消费即可参与一次转盘抽奖,如图,转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时无效,需要重转),若指计指向的数字为4的倍数则可以领取一份奖品,请计算顾客获奖的概率。
18.(8分)在弹性限度内,弹簧的长度随所挂物体质量的增加而伸长,经过实验发现,弹簧的长度y(cm)与所挂物体质量x(kg)之间的对应关系如下表:
所挂物体质量x/kg 0 1 2 3 4 …
弹簧的长度y/cm 12 12.5 13 13.5 14 …
(1)在这个变化过程中,自变量和因变量各是什么?
(2)请根据表格中的数据,求挂物体后弹簧的长度y(cm)与所挂物体质量x(kg)之间的关系式。
(3)在弹性限度内,弹簧伸长后的最大长度为20 cm,该弹簧最多能挂多重的物体?
19.(9分)如图,E,F分别是长方形ABCD的边AD,BC上的点(不与端点重合),连接EF,将四边形EFCD沿EF折叠,点C,D的对应点分别为点C′,D′,若∠AGC′=40°,求∠AEF的度数。
20.(9分)如图,已知△ABC,点D在BC边上。
(1)求作△DEF,使△DEF≌△BCA,并满足点E在BC的延长线上,DF∥AB(请用尺规作图,不写作法,保留作图痕迹);
(2)根据你的作图方法,说明△DEF≌△BCA的理由。
21.(10分)2024年6月2日,锦州迎来了一场体育盛宴——“跑遍辽宁”“奔赴山海前程‘是’锦”2024锦州马拉松赛。这场全民参与的体育盛宴在风景如画的滨河路凌川大桥下拉开帷幕。甲、乙两名选手均参加了10 km健康跑项目(5 km处折返),他们同时出发,两选手所跑的路程y(km)与时间x(min)之间的关系如图所示,请根据图象回答下列问题:
(1)求甲选手前4 km的平均速度。
(2)乙选手追上甲选手时,他们距离终点还有多少千米?
(3)若甲选手跑最后一段的平均速度与他前4 km的平均速度相同,那么当乙选手到达终点时,甲选手还要经过多长时间到达终点?
22.(11分)【方法回顾】
在学习整式的乘法时,我们曾用两种不同的方法,表示同一个长方形的面积,进而得到单项式与多项式相乘的法则,也曾经用两种不同的方法,表示同一个正方形的面积来验证和解释乘法公式,我们将这种方法称为“等积法”。它的基本思想是:将同一个量从两个不同角度计算两次,我们常用“等积法”列出等量关系、求线段长度或线段之间的数量关系。
【方法应用】
(1)如图1,正方形ABCD是由长为a、宽为b的4个全等的小长方形拼摆而成的,我们可以利用该正方形面积的不同表示方法验证一个与完全平方公式相关的等量关系,请你写出这个等量关系。
【方法迁移】
(2)如图2,长方形ABCD是由8个长为a、宽为b的全等的小长方形拼摆而成的,请你根据“等积法”计算两次的基本思想,解答下列问题:
①求a,b之间的数量关系;
②若长方形ABCD的宽AB=40 cm,求小长方形的面积。
【拓展应用】
(3)如图3,在△ABC中,∠ABC=90°,AB=6,BC=8,AC=10,P是△ABC三条角平分线的交点,求点P到边AC的距离。
23.(12分)【问题提出】
期末复习课上,数学丁老师出示了下面一个问题:如图1,在△ABC中,D是BA延长线的点,E是AC边上一点,且满足DE=BC,∠DEA=∠ACB,那么A是BD的中点。请你说明理由。
【思路探究】
小王同学从条件出发分析解题思路:以DE为腰构造等腰三角形DEF和平行八字型全等三角形,如图2,以点D为圆心,以DE长为半径画弧,交CA的延长线于点F,先应用等腰三角形的轴对称性,再应用三角形全等“AAS”(或“ASA”)的判定方法即可得AB=AD;
小张同学从结论出发分析解题思路:以AB为腰构造等腰三角形ABF,将说明AD=AB的问题转化为说明AD=BF的问题,如图3,以点B为圆心,以AB长为半径画弧,交AC于点F,于是可得∠BFA=∠BAF,再应用三角形全等“AAS”(或“ASA”)的判定方法即可得AB=BF=AD。
(1)请你选择小王同学或小张同学的思路或按自己的思路写出完整的解题过程。
【学以致用】
(2)请你在理解了小张同学或小王同学解题思路的基础上,解答下面一道图形较为复杂的同类问题:如图4,在四边形ABCD中,AB=AC=CD,∠ACD=90°,过点B作线段BE⊥AB,且BE=AB,连接DE,交BC的延长线于点F,猜想DF与EF的数量关系并说明理由。
【详解答案】
1.A 解析:A.是轴对称图形,故本选项符合题意;B.不是轴对称图形,故本选项不合题意;C.不是轴对称图形,故本选项不合题意;D.不是轴对称图形,故本选项不合题意。故选A。
2.A 解析:0.000 000 01 m=1×10-8 m。故选A。
3.C 解析:A.抛出的篮球不会下落,是不可能事件,故本选项不符合题意;B.射击运动员射击一次,命中10环是随机事件,故本选项不符合题意;C.早晨太阳从东方升起,是必然事件,故本选项符合题意;D.任意掷一枚硬币,落地后正面向上,是随机事件,故本选项不符合题意。故选C。
4.D 解析:A.x3+5x3=6x3,故A选项错误;B.x6÷x3=x3,故B选项错误;C.(a2)3=a6,故C选项错误;D.(ab)3=a3b3,故D选项正确。故选D。
5.C 解析:如图。因为∠1=∠2=40°,
所以∠4=180°-∠1-∠2=100°。因为两个平面镜平行放置,所以经过两次反射后的光线与入射光线平行,所以∠3=∠4=100°。故选C。
6.D 解析:A.(2x-y)(x+2y)不能用平方差公式计算,故本选项不符合题意;B.(x-y)(y-x)不能用平方差公式计算,故本选项不符合题意;C.(b+a)(b-c)不能用平方差公式计算,故本选项不符合题意;D.(-a+b)(a+b)能用平方差公式计算,故本选项符合题意。故选D。
7.B 解析:如图:
因为直尺的两边平行,∠1=55°,所以∠ABC=∠1=55°,∠ACB=∠2。因为∠BAC=90°,所以∠ACB=180°-∠BAC-∠ABC=180°-90°-55°=35°,所以∠2=∠ACB=35°。故选B。
8.D 解析:因为△AOB≌△OCD,所以∠AOB=∠C,故A选项正确;因为△AOB中,∠B=90°,所以∠A+∠AOB=90°。因为∠AOB=∠C,所以∠A+∠C=90°,故B选项正确;因为△OCD中,∠D=90°,所以∠COD+∠C=90°。因为∠AOB=∠C,所以∠COD+∠AOB=90°,所以∠AOC=90°,所以AO⊥CO,故C选项正确;因为△AOB≌△OCD,所以AO=CO,所以AO≠CD,故D选项错误。故选D。
9.D 解析:①当货车开始进入隧道时,y逐渐变大;当货车完全进入隧道,由于隧道长大于货车长,此时y不变且最大;当货车开始离开隧道时,y逐渐变小。故①正确。②王大爷离家的距离y先逐渐变大,他走的是一段弧线时,此时y不变且最大,之后逐渐离家越来越近直至回家,即y逐渐变小,故②正确。③往空杯中匀速倒水,倒满后停止,水的体积逐渐增加,一段时间后,再匀速倒出杯中的水,这期间,水的体积先保持不变,然后逐渐减少,杯中水的体积y与所用时间x之间的关系符合图象,故③正确。故选D。
10.A 解析:根据作图可知MN为AB的垂直平分线,所以AB=2AM=2BM=4,AN=BN。因为C△ACN=AN+CN+AC=12,所以BN+CN+AC=12,所以C△ABC=AB+BN+CN+AC=4+12=16。故选A。
11. 解析:3-1=。
12.y=25x+1 000 解析:依等量关系式“总费用=老师费用+学生费用”可得y=20×50+25x=25x+1 000。
13.3 解析:设黄球的个数为x,根据题意得==,所以6+x=9,解得x=3。
所以黄球的个数为3。
14.3 解析:因为△ADF≌△CBE,所以AF=CE,所以AF-EF=CE-EF,即AE=CF。因为2AE=AC-EF=8-2=6,所以AE=3。
15. 解析:如图,设AC,BD交于点J,BD,PC交于点O。
因为∠APB=∠CPD=90°,所以∠APC=∠BPD。因为PA=PB,PC=PD,所以△APC≌△BPD(SAS),所以AC=BD,∠ACP=∠BDP。因为∠POD=∠COJ,所以∠CJO=∠OPD=90°,所以AC⊥BD,所以四边形ABCD的面积=·AC2。因为AC≤PA+PC=5,所以四边形ABCD面积的最大值为。
16.解:(1)原式=xy·4x2y4÷x2y4=x3y5÷x2y4=xy。
(2)原式=(a2-4ab+4b2+a2+4ab-ab-4b2)÷2a
=(2a2-ab)÷2a
=a-b。
当a=-1,b=2时,
原式=-1-1=-2。
17.解:由题意可知,任意转动一次转盘,指针指向的数字共有12种可能的结果,因为转盘是12等份,所以每种结果出现的可能性相同,其中指针指向数字是4的倍数的结果有3种,分别是4,8,12。
所以P(顾客获奖)==。
18.解:(1)自变量是所挂物体质量,因变量是弹簧的长度。
(2)由表格数据可知,x每增加1 kg,y就增加0.5 cm,
所以挂物体后弹簧的长度y与所挂物体的质量x之间的关系式为y=12+0.5x。
(3)令y=20,则12+0.5x=20,
解得x=16,
所以该弹簧最多能挂16 kg的物体。
19.解:因为长方形ABCD,
所以AD∥BC,所以∠BFG=∠AGC′=40°,∠AEF=∠EFC,
所以∠CFG=180°-∠BFG=140°。
由折叠性质可知∠GFE=∠EFC=∠CFG,
所以∠EFC=×140°=70°,
所以∠AEF=70°。
20.解:(1)如图所示即为所求。
(2)根据作图得DF=AB,∠FDE=∠B,DE=BC,
所以△DEF≌△BCA(SAS)。
21.解:(1)根据题图可知,v甲=4÷10=(km/min)。
答:甲选手前4 km的平均速度为 km/min。
(2)由题图可知,v乙=10÷50=(km/min),
乙选手追上甲选手时,他们距离终点的路程s=×(50-30)=4(km)。
答:乙选手追上甲选手时,他们距离终点还有4 km。
(3)由题图可知,甲最后的冲刺阶段距离终点还有10-8=2(km),
所以t甲=2÷=5(min)。
答:乙选手到达终点时,甲选手还要经过5 min到达终点。
22.解:(1)大正方形的边长为(a+b),面积为(a+b)2;小正方形的边长为(a-b),面积为(a-b)2;4个长方形的面积之和为4ab,所以(a+b)2=(a-b)2+4ab。
(2)①因为长方形ABCD的面积为2a·(a+b),小长方形的面积为ab,
所以2a·(a+b)=8ab,即2a2+2ab=8ab,所以2a2-6ab=0,即a2-3ab=0。
因为a≠0,所以a2=3ab,所以a=3b。
②因为AB=40 cm,所以a+b=40 cm,
所以3b+b=40 cm,
解得b=10 cm,所以a=3b=30 cm,
所以小长方形的面积为ab=30×10=300(cm2)。
(3)设点P到边AC的距离为h。
因为点P是△ABC三条角平分线的交点,
所以点P到边AB的距离,到边BC的距离都等于点P到边AC的距离,
即点P到边AB的距离为h,到边BC的距离为h。
因为在△ABC中,∠ABC=90°,AB=6,BC=8,
所以S△ABC=×6×8=24。
因为S△ABC=S△PAC+S△PBC+S△PAB
=AC·h+BC·h+AB·h,
=×10h+×8h+×6h
=12h,
所以12h=24,解得h=2,即点P到边AC的距离为2。
23.解:(1)小王同学的思路:
如题图2,以点D为圆心,以DE长为半径画弧,交CA的延长线于点F,则DF=DE。
所以∠F=∠DEA。
因为∠DEA=∠ACB,DE=BC,
所以∠F=∠ACB,DF=BC。
因为∠DAF=∠BAC,
所以△DAF≌△BAC(AAS),
所以AD=AB,即A是BD的中点。
小张同学的思路:
如题图3,以点B为圆心,以AB长为半径画弧,交AC于点F,连接BF,则BF=AB,
所以∠BAF=∠AFB。
因为∠DAE=180°-∠BAF,∠BFC=180°-∠AFB,
所以∠DAE=∠BFC。
因为∠DEA=∠ACB,DE=BC,
所以△DEA≌△BCF(AAS),所以AD=BF,
所以AB=AD,即A是BD的中点。
(答案不唯一)
(2)猜想DF=EF。理由:
方法1:如图1,以点D为圆心,CD长为半径作弧,交BF的延长线于点M,连接DM,
图1
则DM=DC,所以∠M=∠DCM。
因为AB=AC=CD=DM,∠ACD=90°,EB=BA,EB⊥BA,
所以DM=BE,∠ABC=∠ACB,∠ACB+∠DCM=90°,∠ABE=90°,
所以∠ABC+∠EBF=90°,
所以∠M=∠DCM=∠EBF。
又因为∠DFM=∠EFB,所以△DFM≌△EFB(AAS),所以DF=EF。
方法2:如图2,以点E为圆心,以EF长为半径画弧,交BF于点N,连接EN,则EN=EF,所以∠EFN=∠ENF。
因为∠CFD=180°-∠EFN,∠BNE=180°-∠ENF,所以∠CFD=∠BNE。
因为AB=AC,∠ACD=90°,EB⊥BA,
所以∠ABC=∠ACB,∠ACB+∠DCF=90°,∠ABE=90°,
图2
所以∠ABC+∠EBF=90°,
所以∠DCF=∠EBF。
因为AB=CD=BE,
所以△DCF≌△EBN(AAS),所以DF=EN,所以DF=EF。
同课章节目录
