期末评估测试卷B (含答案)2024-2025学年数学北师版七年级下册
文档属性
| 名称 | 期末评估测试卷B (含答案)2024-2025学年数学北师版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 426.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 00:00:00 | ||
图片预览



文档简介
期末评估测试卷B
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024齐齐哈尔中考)下列计算正确的是( )
A.4a2+2a2=6a4
B.5a·2a=10a
C.a6÷a2=a3
D.(-a2)2=a4
2.视力表中的字母“E”有各种不同的摆放形式,下面每种组合的两个字母“E”是关于某条直线成轴对称的是( )
3.现有两根长度分别为3 cm和7 cm的木棒,若要钉成一个三角形木架,则应选取的第三根木棒长为( )
A.4 cm B.7 cm C.10 cm D.13 cm
4.长方形的长为6x2y,宽为3xy,则它的面积为( )
A.9x3y2 B.18x3y2
C.18x2y D.6xy2
5.如图,在△ABC和△DEF中,
∠A=∠D,AC=DF,要使得△ABC≌△DEF,还需要补充一个条件,则下列错误的条件是( )
A.BF=CE B.AC∥DF
C.∠B=∠E D.AB=DE
6.任意掷一枚骰子,下列情况出现的可能性比较大的是( )
A.面朝上的点数是3
B.面朝上的点数是奇数
C.面朝上的点数小于2
D.面朝上的点数小于3
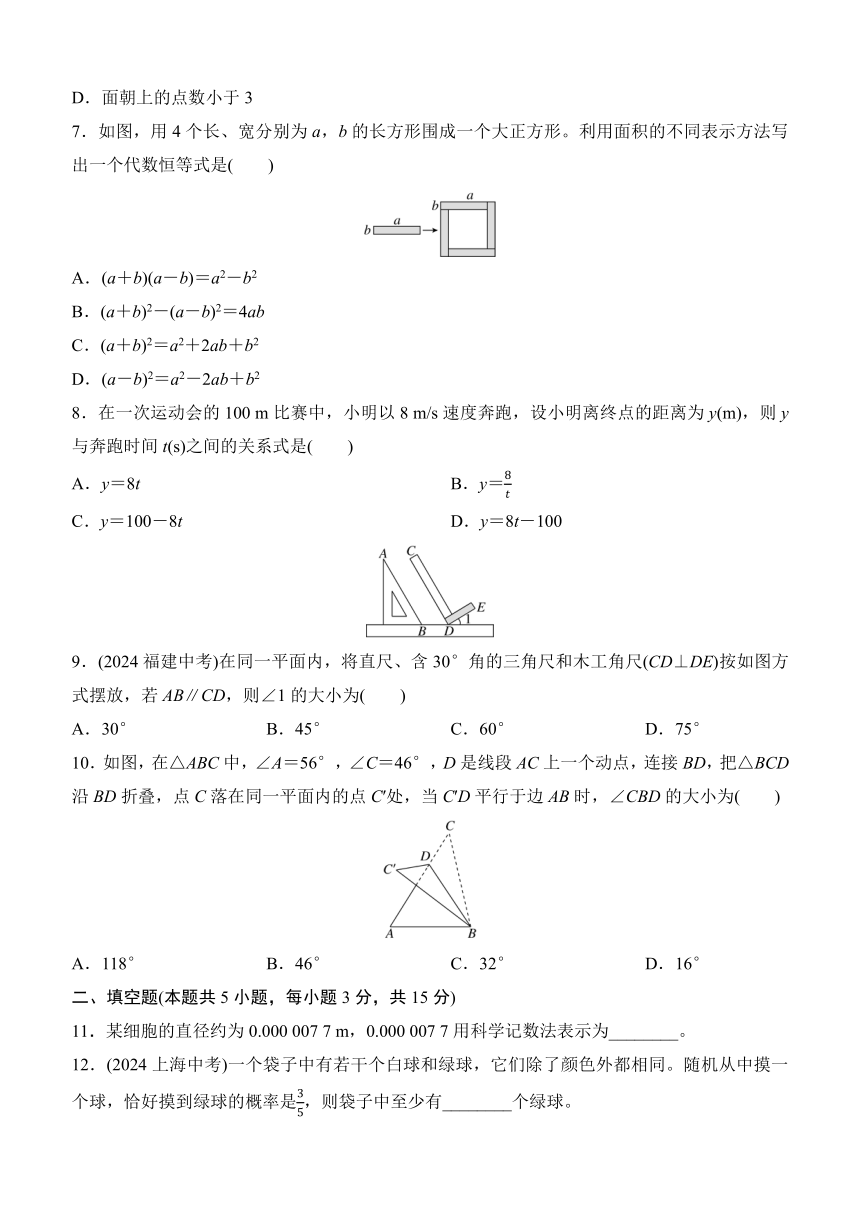
7.如图,用4个长、宽分别为a,b的长方形围成一个大正方形。利用面积的不同表示方法写出一个代数恒等式是( )
A.(a+b)(a-b)=a2-b2
B.(a+b)2-(a-b)2=4ab
C.(a+b)2=a2+2ab+b2
D.(a-b)2=a2-2ab+b2
8.在一次运动会的100 m比赛中,小明以8 m/s速度奔跑,设小明离终点的距离为y(m),则y与奔跑时间t(s)之间的关系式是( )
A.y=8t B.y=
C.y=100-8t D.y=8t-100
9.(2024福建中考)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为( )
A.30° B.45° C.60° D.75°
10.如图,在△ABC中,∠A=56°,∠C=46°,D是线段AC上一个动点,连接BD,把△BCD沿BD折叠,点C落在同一平面内的点C′处,当C′D平行于边AB时,∠CBD的大小为( )
A.118° B.46° C.32° D.16°
二、填空题(本题共5小题,每小题3分,共15分)
11.某细胞的直径约为0.000 007 7 m,0.000 007 7用科学记数法表示为________。
12.(2024上海中考)一个袋子中有若干个白球和绿球,它们除了颜色外都相同。随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有________个绿球。
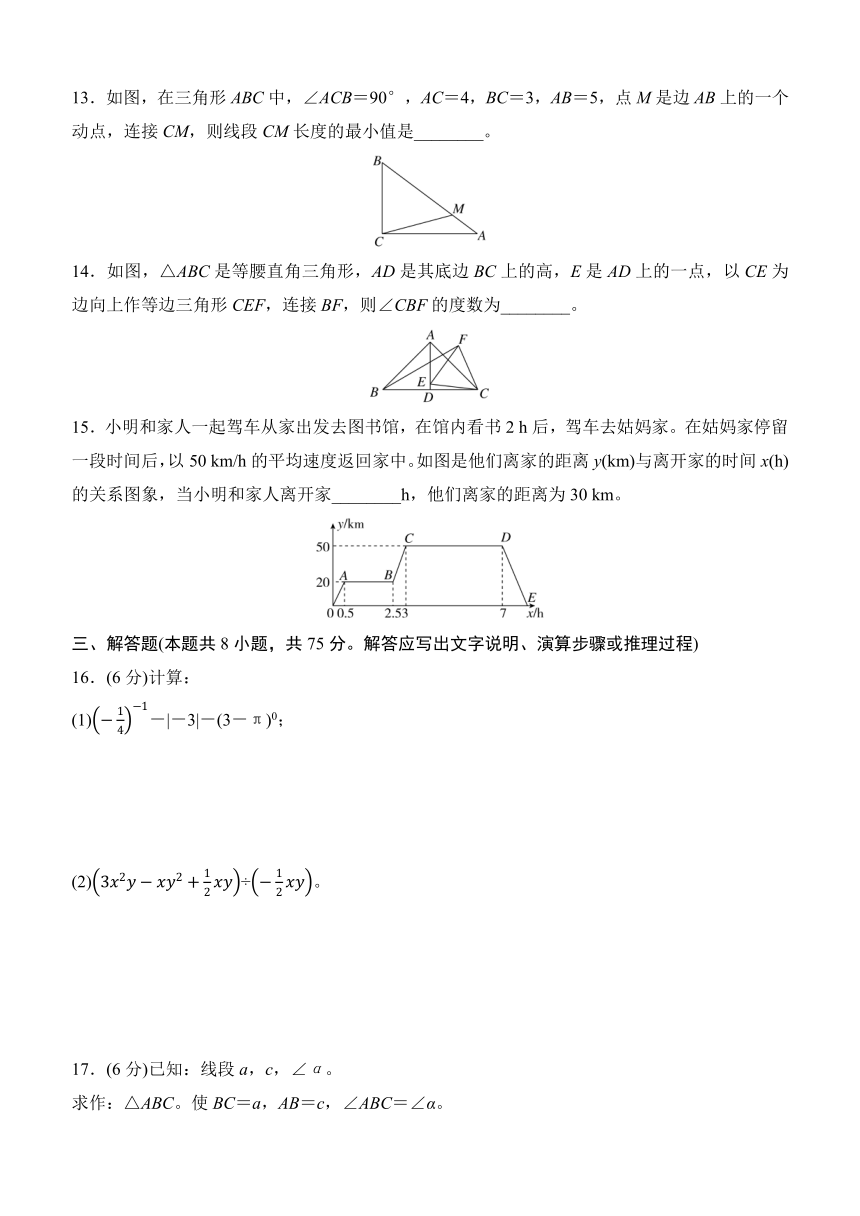
13.如图,在三角形ABC中,∠ACB=90°,AC=4,BC=3,AB=5,点M是边AB上的一个动点,连接CM,则线段CM长度的最小值是________。
14.如图,△ABC是等腰直角三角形,AD是其底边BC上的高,E是AD上的一点,以CE为边向上作等边三角形CEF,连接BF,则∠CBF的度数为________。
15.小明和家人一起驾车从家出发去图书馆,在馆内看书2 h后,驾车去姑妈家。在姑妈家停留一段时间后,以50 km/h的平均速度返回家中。如图是他们离家的距离y(km)与离开家的时间x(h)的关系图象,当小明和家人离开家________h,他们离家的距离为30 km。
三、解答题(本题共8小题,共75分。解答应写出文字说明、演算步骤或推理过程)
16.(6分)计算:
(1)-|-3|-(3-π)0;
(2)÷。
17.(6分)已知:线段a,c,∠α。
求作:△ABC。使BC=a,AB=c,∠ABC=∠α。
18.(8分)如图,分别过△ABC的顶点A,B作AD∥BE。若∠CAD=25°,∠EBC=80°,求∠ACB的度数。
19.(9分)从背面相同的同一副扑克牌中取出9张红桃、10张黑桃、11张方块。
(1)将取出的这些牌洗匀背面朝上放在桌面上,求从中随机抽出一张是红桃的概率;
(2)若先从取出的这些牌中抽掉6张红桃和m张黑桃后,将剩下的牌洗匀背面朝上放在桌面上,从中再随机抽出一张牌,若抽取黑桃牌的概率为,求m的值。
20.(9分)如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,连接BE,CD相交于点F。
(1)试说明:BE=CD;
(2)若BE=7.5 cm,DF=2.4 cm,求CF的长。
21.(11分)一个水果零售商在批发市场按每千克1.8元批发了若干千克西瓜出售,为了方便,他带了一些零钱备用。他先按市场价售出一些后,又降价出售。售出的西瓜质量x(kg)与他手中持有的钱数y(元)(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)零售商自带的零钱是多少?
(2)降价前每千克西瓜的价格是多少?
(3)随后他按每千克降价0.5元将剩余的西瓜售完,这时他手中的钱(含备用零钱)是450元,他一共批发了多少千克西瓜?
(4)这个水果零售商一共赚了多少钱?
22.(12分)(1)如图1,是一个长和宽分别为m,n的长方形纸片,如果它的长和宽分别增加a,b,所得如图2长方形,用不同的方法表示这个长方形的面积,得到的等式为(m+a)·(n+b)=________________。
(2)①如图3,是几个小正方形和小长方形拼成的一个边长为a+b+c的大正方形,用不同的方法表示这个大正方形的面积,得到的等式为(a+b+c)2=________________________________________________________________________;
②已知a+b+c=15,a2+b2+c2=77,利用①中所得到的等式,求代数式ab+bc+ac的值。
(3)如图4,是用2个小正方体和6个小长方体拼成的一个棱长为a+b的大正方体,通过用不同的方法表示这个大正方体的体积,求当a+b=5.9,ab=4.5时,代数式a3+b3的值。
23.(14分)在△ABC中,AB=AC,∠BAC=α,作射线AP,点C关于直线AP的对称点为D,连接AD,直线DC,DB分别交AP于点E,F,连接CF。
(1)如图1,射线AP在△ABC的外部,当α=40°时,求∠BDC的度数。
(2)如图2,射线AP的一部分落在△ABC内部,当α=60°时,
①直接写出∠BDC的度数;
②试说明:AF=BF+CF。
(3)当α=60°时,若△DBC是等腰三角形,直接写出∠CAD的度数。
【详解答案】
1.D 解析:A.4a2+2a2=6a2,故本选项不符合题意;B.5a·2a=10a2,故本选项不符合题意;C.a6÷a2=a4,故本选项不符合题意;D.(-a2)2=a4,故本选项符合题意。故选D。
2.D 解析:A,B,C选项中,两个字母“E”不能关于某条直线成轴对称,而D选项中,两个字母“E”能沿着直线翻折互相重合,所以选项D符合题意。故选D。
3.B 解析:设此三角形第三条边长为a cm,由三角形任意两边之和大于第三边,任意两边之差小于第三边可知,第三根木棒长的范围应为44.B 解析:因为长方形的长为6x2y,宽为3xy,所以长方形的面积=6x2y·3xy=18x3y2。故选B。
5.A 解析:A.添加BF=CE,可得,BC=EF,不能得出△ABC≌△DEF,符合题意;B.添加AC∥DF,可得,∠ACB=∠DFE,利用ASA得出△ABC≌△DEF,不符合题意;C.添加∠B=∠E,利用AAS得出△ABC≌△DEF,不符合题意;D.添加AB=DE,利用SAS得出△ABC≌△DEF,不符合题意。故选A。
6.B 解析:A.面朝上的点数是3的概率为;B.面朝上的点数是奇数的概率为=;C.面朝上的点数小于2的概率为;D.面朝上的点数小于3的概率为=。所以概率最大的是面朝上的点数是奇数。故选B。
7.B 解析:右边阴影部分的面积是(a+b)2-(a-b)2;4个长方形的面积是4ab,则验证的等式是(a+b)2-(a-b)2=4ab。故选B。
8.C 解析:由题意得y=100-8t。故选C。
9.A 解析:因为AB∥CD,所以∠CDB=∠ABF=60°。因为CD⊥DE,所以∠CDE=90°,所以∠1=180°-60°-90°=30°。故选A。
10.D 解析:当C′D∥AB时,如图,
所以∠C′DA=∠A=56°,所以∠C′DC=180°-∠C′DA=124°。
由折叠的性质可得,∠CDB=∠C′DB==118°,所以∠CBD=180°-118°-46°=16°。故选D。
11.7.7×10-6 解析:0.000 007 7=7.7×10-6。
12.3 解析:因为一个袋子中有若干个白球和绿球,随机从中摸一个球,恰好摸到绿球的概率是,所以袋子中至少有3个绿球。
13. 解析:当CM⊥AB时,CM最短。因为∠ACB=90°,AC=4,BC=3,AB=5,所以4×3=5CM,所以CM==。
14.30° 解析:如图,连接BE并延长交CF于点H。
因为△ABC是等腰直角三角形,AD⊥BC,所以AD是BC的垂直平分线,所以EB=EC,所以∠EBC=∠ECB。因为△CEF是等边三角形,所以∠FEC=60°,EF=EC,所以EF=EB,所以∠FBE=∠EFB。因为∠FEH=180°-∠BEF=∠FBE+∠EFB,∠CEH=180°-∠BEC=∠EBC+∠ECB,所以∠FEC=∠FEH+∠CEH=∠FBE+
∠EFB+∠EBC+∠ECB=2∠FBE+2∠EBC=2∠CBF,所以∠CBF=∠FEC=30°。
15.或 解析:驾车去姑妈家的速度是(50-20)÷(3-2.5)=60(km/h),2.5+(30-20)÷60=(h),7+(50-30)÷50=(h),所以当小明和家人离开家或 h时,他们离家的距离为30 km。
16.解:(1)原式=-4-3-1=-8。
(2)原式=3x2y÷-xy2÷+xy÷=-6x+2y-1。
17.解:如图所示。①先画射线BM,②以∠α的顶点B′为圆心,任意长为半径画弧,分别交∠α的两边于点A′,C′,③以B为圆心,相同长度为半径画弧,交BC于点F,④以F为圆心,C′A′长为半径画弧,交前弧于点E,画射线BN;⑤在射线BM上取点C,使CB=a,以B为圆心,c为半径画弧交射线BN于点A,连接AC。结论:△ABC即为所求三角形。
18.解:因为AD∥BE,
所以∠ADC=∠EBC=80°。
因为∠CAD=25°,所以∠ACB=180°-∠CAD-∠ADC=75°,
所以∠ACB的度数为75°。
19.解:(1)因为9+10+11=30,所以从中随机抽出一张牌,共有30种等可能结果,其中出现红桃的有9种结果,
所以从中随机抽出一张是红桃的概率是=。
(2)因为9+10+11-6-m=24-m,
所以抽掉6张红桃和m张黑桃后,桌面上共有(24-m)张牌,其中黑桃有(10-m)张,
所以从中再随机抽出一张牌,共有(24-m)种等可能结果,其中出现黑桃的有(10-m)种结果,
又因为抽取黑桃牌的概率为。
所以(24-m)=10-m,
解得m=3,
所以m的值为3。
20.解:(1)因为D,E分别是AB,AC的中点,
所以AD=AB,AE=AC。
因为AB=AC,所以AD=AE。
在△ABE和△ACD中,
所以△ABE≌△ACD(SAS),所以BE=CD。
(2)因为CD=BE=7.5 cm,所以CF=CD-DF=7.5-2.4=5.1(cm)。
21.解:(1)零售商自带的零钱是50元。
(2)(330-50)÷80=280÷80=3.5(元)。
答:降价前每千克西瓜的价格是3.5元。
(3)(450-330)÷(3.5-0.5)=120÷3=40(kg),
80+40=120(kg)。
答:他一共批发了120 kg西瓜。
(4)450-120×1.8-50=184(元)。
答:这个水果零售商一共赚了184元。
22.解:(1)mn+mb+na+ab
(2)①a2+b2+c2+2(ab+bc+ac)
②因为a+b+c=15,a2+b2+c2=77,
所以152=77+2(ab+bc+ac),
所以ab+bc+ac=74。
(3)如题图4,是用2个小正方体和6个小长方体拼成 的一个棱长为a+b的大正方体,
整体上大正方体的体积为(a+b)3。
组成大正方体的2个小正方体和6个小长方体的体积的和为a3+3a2b+3ab2+b3,
所以得到的等式为(a+b)3=a3+3a2b+3ab2+b3。
因为a+b=5.9,ab=4.5,
所以a3+b3
=(a+b)3-3a2b-3ab2
=(a+b)3-3ab(a+b)
=5.93-3×4.5×5.9
=205.379-79.65
=125.729。
23.解:(1)因为点C与点D关于直线AP对称,
所以∠CAE=∠DAE,AC=AD。
因为AB=AC,∠BAC=α=40°,
所以∠ABC=∠ACB=70°,
AB=AC=AD。
设∠CAE=∠DAE=β,则∠BAD=40°+2β,
所以∠ADB=∠ABD==70°-β,∠ADC=∠ACD==90°-β,
所以∠BDC=∠ADC-∠ADB=90°-β-(70°-β)=20°。
(2)①∠BDC的度数为30°。
②如图1,将AF绕点A逆时针旋转60°得到AG,连接CG,
因为∠FAG=60°,AF=AG,所以△AFG是等边三角形,所以AF=FG=AG。
因为∠BAC=60°,
所以∠BAF=∠CAG=60°-∠CAF。
因为AB=AC,AF=AG,
所以△ABF≌△ACG(SAS),
所以BF=CG,∠ABF=∠ACG。
由①知∠BDC=30°,因为AF是点C与点D的对称轴,所以∠DEF=∠CEF=90°,∠BDC=∠ECF=30°,
所以∠DFE=60°=∠CFE,
所以∠BFC=120°。
因为∠BAC=60°,
所以∠ABF+∠ACF=180°,
所以∠ACF+∠ACG=180°,即F,C,G三点在同一条直线上,
所以FG=CF+CG=CF+BF,
所以AF=BF+CF。
(3)∠CAD的度数为120°或60°或30°或150°。
解析:①因为α=60°,AB=AC,
所以△ABC是等边三角形,
所以AB=AC=BC。
如图2,当AP与AB重合时,BD=BC,此时∠CAD=2∠BAC=120°;
②如图3,△ACD是等边三角形时,AC=AD=CB,此时∠CAD=∠CAB=60°;
③如图4,当点D落在BC的垂直平分线上,且在BC下方时,DB=DC,
因为△ABC是等边三角形,
所以∠CAD=∠CAB=30°;
④如图5,当点D落在BC的垂直平分线上,且在BC上方时,DB=DC,
此时∠CAD=180°-30°=150°。
综上所述,∠CAD的度数为120°或60°或30°或150°。
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024齐齐哈尔中考)下列计算正确的是( )
A.4a2+2a2=6a4
B.5a·2a=10a
C.a6÷a2=a3
D.(-a2)2=a4
2.视力表中的字母“E”有各种不同的摆放形式,下面每种组合的两个字母“E”是关于某条直线成轴对称的是( )
3.现有两根长度分别为3 cm和7 cm的木棒,若要钉成一个三角形木架,则应选取的第三根木棒长为( )
A.4 cm B.7 cm C.10 cm D.13 cm
4.长方形的长为6x2y,宽为3xy,则它的面积为( )
A.9x3y2 B.18x3y2
C.18x2y D.6xy2
5.如图,在△ABC和△DEF中,
∠A=∠D,AC=DF,要使得△ABC≌△DEF,还需要补充一个条件,则下列错误的条件是( )
A.BF=CE B.AC∥DF
C.∠B=∠E D.AB=DE
6.任意掷一枚骰子,下列情况出现的可能性比较大的是( )
A.面朝上的点数是3
B.面朝上的点数是奇数
C.面朝上的点数小于2
D.面朝上的点数小于3
7.如图,用4个长、宽分别为a,b的长方形围成一个大正方形。利用面积的不同表示方法写出一个代数恒等式是( )
A.(a+b)(a-b)=a2-b2
B.(a+b)2-(a-b)2=4ab
C.(a+b)2=a2+2ab+b2
D.(a-b)2=a2-2ab+b2
8.在一次运动会的100 m比赛中,小明以8 m/s速度奔跑,设小明离终点的距离为y(m),则y与奔跑时间t(s)之间的关系式是( )
A.y=8t B.y=
C.y=100-8t D.y=8t-100
9.(2024福建中考)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为( )
A.30° B.45° C.60° D.75°
10.如图,在△ABC中,∠A=56°,∠C=46°,D是线段AC上一个动点,连接BD,把△BCD沿BD折叠,点C落在同一平面内的点C′处,当C′D平行于边AB时,∠CBD的大小为( )
A.118° B.46° C.32° D.16°
二、填空题(本题共5小题,每小题3分,共15分)
11.某细胞的直径约为0.000 007 7 m,0.000 007 7用科学记数法表示为________。
12.(2024上海中考)一个袋子中有若干个白球和绿球,它们除了颜色外都相同。随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有________个绿球。
13.如图,在三角形ABC中,∠ACB=90°,AC=4,BC=3,AB=5,点M是边AB上的一个动点,连接CM,则线段CM长度的最小值是________。
14.如图,△ABC是等腰直角三角形,AD是其底边BC上的高,E是AD上的一点,以CE为边向上作等边三角形CEF,连接BF,则∠CBF的度数为________。
15.小明和家人一起驾车从家出发去图书馆,在馆内看书2 h后,驾车去姑妈家。在姑妈家停留一段时间后,以50 km/h的平均速度返回家中。如图是他们离家的距离y(km)与离开家的时间x(h)的关系图象,当小明和家人离开家________h,他们离家的距离为30 km。
三、解答题(本题共8小题,共75分。解答应写出文字说明、演算步骤或推理过程)
16.(6分)计算:
(1)-|-3|-(3-π)0;
(2)÷。
17.(6分)已知:线段a,c,∠α。
求作:△ABC。使BC=a,AB=c,∠ABC=∠α。
18.(8分)如图,分别过△ABC的顶点A,B作AD∥BE。若∠CAD=25°,∠EBC=80°,求∠ACB的度数。
19.(9分)从背面相同的同一副扑克牌中取出9张红桃、10张黑桃、11张方块。
(1)将取出的这些牌洗匀背面朝上放在桌面上,求从中随机抽出一张是红桃的概率;
(2)若先从取出的这些牌中抽掉6张红桃和m张黑桃后,将剩下的牌洗匀背面朝上放在桌面上,从中再随机抽出一张牌,若抽取黑桃牌的概率为,求m的值。
20.(9分)如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,连接BE,CD相交于点F。
(1)试说明:BE=CD;
(2)若BE=7.5 cm,DF=2.4 cm,求CF的长。
21.(11分)一个水果零售商在批发市场按每千克1.8元批发了若干千克西瓜出售,为了方便,他带了一些零钱备用。他先按市场价售出一些后,又降价出售。售出的西瓜质量x(kg)与他手中持有的钱数y(元)(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)零售商自带的零钱是多少?
(2)降价前每千克西瓜的价格是多少?
(3)随后他按每千克降价0.5元将剩余的西瓜售完,这时他手中的钱(含备用零钱)是450元,他一共批发了多少千克西瓜?
(4)这个水果零售商一共赚了多少钱?
22.(12分)(1)如图1,是一个长和宽分别为m,n的长方形纸片,如果它的长和宽分别增加a,b,所得如图2长方形,用不同的方法表示这个长方形的面积,得到的等式为(m+a)·(n+b)=________________。
(2)①如图3,是几个小正方形和小长方形拼成的一个边长为a+b+c的大正方形,用不同的方法表示这个大正方形的面积,得到的等式为(a+b+c)2=________________________________________________________________________;
②已知a+b+c=15,a2+b2+c2=77,利用①中所得到的等式,求代数式ab+bc+ac的值。
(3)如图4,是用2个小正方体和6个小长方体拼成的一个棱长为a+b的大正方体,通过用不同的方法表示这个大正方体的体积,求当a+b=5.9,ab=4.5时,代数式a3+b3的值。
23.(14分)在△ABC中,AB=AC,∠BAC=α,作射线AP,点C关于直线AP的对称点为D,连接AD,直线DC,DB分别交AP于点E,F,连接CF。
(1)如图1,射线AP在△ABC的外部,当α=40°时,求∠BDC的度数。
(2)如图2,射线AP的一部分落在△ABC内部,当α=60°时,
①直接写出∠BDC的度数;
②试说明:AF=BF+CF。
(3)当α=60°时,若△DBC是等腰三角形,直接写出∠CAD的度数。
【详解答案】
1.D 解析:A.4a2+2a2=6a2,故本选项不符合题意;B.5a·2a=10a2,故本选项不符合题意;C.a6÷a2=a4,故本选项不符合题意;D.(-a2)2=a4,故本选项符合题意。故选D。
2.D 解析:A,B,C选项中,两个字母“E”不能关于某条直线成轴对称,而D选项中,两个字母“E”能沿着直线翻折互相重合,所以选项D符合题意。故选D。
3.B 解析:设此三角形第三条边长为a cm,由三角形任意两边之和大于第三边,任意两边之差小于第三边可知,第三根木棒长的范围应为4
5.A 解析:A.添加BF=CE,可得,BC=EF,不能得出△ABC≌△DEF,符合题意;B.添加AC∥DF,可得,∠ACB=∠DFE,利用ASA得出△ABC≌△DEF,不符合题意;C.添加∠B=∠E,利用AAS得出△ABC≌△DEF,不符合题意;D.添加AB=DE,利用SAS得出△ABC≌△DEF,不符合题意。故选A。
6.B 解析:A.面朝上的点数是3的概率为;B.面朝上的点数是奇数的概率为=;C.面朝上的点数小于2的概率为;D.面朝上的点数小于3的概率为=。所以概率最大的是面朝上的点数是奇数。故选B。
7.B 解析:右边阴影部分的面积是(a+b)2-(a-b)2;4个长方形的面积是4ab,则验证的等式是(a+b)2-(a-b)2=4ab。故选B。
8.C 解析:由题意得y=100-8t。故选C。
9.A 解析:因为AB∥CD,所以∠CDB=∠ABF=60°。因为CD⊥DE,所以∠CDE=90°,所以∠1=180°-60°-90°=30°。故选A。
10.D 解析:当C′D∥AB时,如图,
所以∠C′DA=∠A=56°,所以∠C′DC=180°-∠C′DA=124°。
由折叠的性质可得,∠CDB=∠C′DB==118°,所以∠CBD=180°-118°-46°=16°。故选D。
11.7.7×10-6 解析:0.000 007 7=7.7×10-6。
12.3 解析:因为一个袋子中有若干个白球和绿球,随机从中摸一个球,恰好摸到绿球的概率是,所以袋子中至少有3个绿球。
13. 解析:当CM⊥AB时,CM最短。因为∠ACB=90°,AC=4,BC=3,AB=5,所以4×3=5CM,所以CM==。
14.30° 解析:如图,连接BE并延长交CF于点H。
因为△ABC是等腰直角三角形,AD⊥BC,所以AD是BC的垂直平分线,所以EB=EC,所以∠EBC=∠ECB。因为△CEF是等边三角形,所以∠FEC=60°,EF=EC,所以EF=EB,所以∠FBE=∠EFB。因为∠FEH=180°-∠BEF=∠FBE+∠EFB,∠CEH=180°-∠BEC=∠EBC+∠ECB,所以∠FEC=∠FEH+∠CEH=∠FBE+
∠EFB+∠EBC+∠ECB=2∠FBE+2∠EBC=2∠CBF,所以∠CBF=∠FEC=30°。
15.或 解析:驾车去姑妈家的速度是(50-20)÷(3-2.5)=60(km/h),2.5+(30-20)÷60=(h),7+(50-30)÷50=(h),所以当小明和家人离开家或 h时,他们离家的距离为30 km。
16.解:(1)原式=-4-3-1=-8。
(2)原式=3x2y÷-xy2÷+xy÷=-6x+2y-1。
17.解:如图所示。①先画射线BM,②以∠α的顶点B′为圆心,任意长为半径画弧,分别交∠α的两边于点A′,C′,③以B为圆心,相同长度为半径画弧,交BC于点F,④以F为圆心,C′A′长为半径画弧,交前弧于点E,画射线BN;⑤在射线BM上取点C,使CB=a,以B为圆心,c为半径画弧交射线BN于点A,连接AC。结论:△ABC即为所求三角形。
18.解:因为AD∥BE,
所以∠ADC=∠EBC=80°。
因为∠CAD=25°,所以∠ACB=180°-∠CAD-∠ADC=75°,
所以∠ACB的度数为75°。
19.解:(1)因为9+10+11=30,所以从中随机抽出一张牌,共有30种等可能结果,其中出现红桃的有9种结果,
所以从中随机抽出一张是红桃的概率是=。
(2)因为9+10+11-6-m=24-m,
所以抽掉6张红桃和m张黑桃后,桌面上共有(24-m)张牌,其中黑桃有(10-m)张,
所以从中再随机抽出一张牌,共有(24-m)种等可能结果,其中出现黑桃的有(10-m)种结果,
又因为抽取黑桃牌的概率为。
所以(24-m)=10-m,
解得m=3,
所以m的值为3。
20.解:(1)因为D,E分别是AB,AC的中点,
所以AD=AB,AE=AC。
因为AB=AC,所以AD=AE。
在△ABE和△ACD中,
所以△ABE≌△ACD(SAS),所以BE=CD。
(2)因为CD=BE=7.5 cm,所以CF=CD-DF=7.5-2.4=5.1(cm)。
21.解:(1)零售商自带的零钱是50元。
(2)(330-50)÷80=280÷80=3.5(元)。
答:降价前每千克西瓜的价格是3.5元。
(3)(450-330)÷(3.5-0.5)=120÷3=40(kg),
80+40=120(kg)。
答:他一共批发了120 kg西瓜。
(4)450-120×1.8-50=184(元)。
答:这个水果零售商一共赚了184元。
22.解:(1)mn+mb+na+ab
(2)①a2+b2+c2+2(ab+bc+ac)
②因为a+b+c=15,a2+b2+c2=77,
所以152=77+2(ab+bc+ac),
所以ab+bc+ac=74。
(3)如题图4,是用2个小正方体和6个小长方体拼成 的一个棱长为a+b的大正方体,
整体上大正方体的体积为(a+b)3。
组成大正方体的2个小正方体和6个小长方体的体积的和为a3+3a2b+3ab2+b3,
所以得到的等式为(a+b)3=a3+3a2b+3ab2+b3。
因为a+b=5.9,ab=4.5,
所以a3+b3
=(a+b)3-3a2b-3ab2
=(a+b)3-3ab(a+b)
=5.93-3×4.5×5.9
=205.379-79.65
=125.729。
23.解:(1)因为点C与点D关于直线AP对称,
所以∠CAE=∠DAE,AC=AD。
因为AB=AC,∠BAC=α=40°,
所以∠ABC=∠ACB=70°,
AB=AC=AD。
设∠CAE=∠DAE=β,则∠BAD=40°+2β,
所以∠ADB=∠ABD==70°-β,∠ADC=∠ACD==90°-β,
所以∠BDC=∠ADC-∠ADB=90°-β-(70°-β)=20°。
(2)①∠BDC的度数为30°。
②如图1,将AF绕点A逆时针旋转60°得到AG,连接CG,
因为∠FAG=60°,AF=AG,所以△AFG是等边三角形,所以AF=FG=AG。
因为∠BAC=60°,
所以∠BAF=∠CAG=60°-∠CAF。
因为AB=AC,AF=AG,
所以△ABF≌△ACG(SAS),
所以BF=CG,∠ABF=∠ACG。
由①知∠BDC=30°,因为AF是点C与点D的对称轴,所以∠DEF=∠CEF=90°,∠BDC=∠ECF=30°,
所以∠DFE=60°=∠CFE,
所以∠BFC=120°。
因为∠BAC=60°,
所以∠ABF+∠ACF=180°,
所以∠ACF+∠ACG=180°,即F,C,G三点在同一条直线上,
所以FG=CF+CG=CF+BF,
所以AF=BF+CF。
(3)∠CAD的度数为120°或60°或30°或150°。
解析:①因为α=60°,AB=AC,
所以△ABC是等边三角形,
所以AB=AC=BC。
如图2,当AP与AB重合时,BD=BC,此时∠CAD=2∠BAC=120°;
②如图3,△ACD是等边三角形时,AC=AD=CB,此时∠CAD=∠CAB=60°;
③如图4,当点D落在BC的垂直平分线上,且在BC下方时,DB=DC,
因为△ABC是等边三角形,
所以∠CAD=∠CAB=30°;
④如图5,当点D落在BC的垂直平分线上,且在BC上方时,DB=DC,
此时∠CAD=180°-30°=150°。
综上所述,∠CAD的度数为120°或60°或30°或150°。
同课章节目录
