期中评估测试卷(含答案) 2024-2025学年数学北师版七年级下册
文档属性
| 名称 | 期中评估测试卷(含答案) 2024-2025学年数学北师版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 626.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 00:00:00 | ||
图片预览




文档简介
期中评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,下列说法正确的是( )
A.∠2与∠3是同旁内角
B.∠1与∠2是同位角
C.∠1与∠3是同位角
D.∠1与∠2是内错角
2.(2024烟台中考)下列计算结果为a6的是( )
A.a2·a3 B.a12÷a2
C.a3+a3 D.(a2)3
3.在科幻小说《三体》中,制造太空电梯的材料是由科学家汪淼发明的一种具有超高强度纳米丝的“飞刃”。若“飞刃”的直径为0.000 92 dm,则“飞刃”的直径(dm)可用科学记数法表示为( )
A.9.2×10-4 B.92×10-3
C.0.92×10-3 D.-9.2×104
4.(2024宿迁中考)如图,直线AB∥CD,直线MN分别与直线AB,CD交于点E,F,且∠1=40°,则∠2等于( )
A.120° B.130° C.140° D.150°
5.如图,点E在CD延长线上,下列条件中能判定AB∥CE的是( )
A.∠5=∠C
B.∠1=∠2
C.∠B=∠C
D.∠C+∠CAB=180°
6.箱内有50颗白球和10颗红球,小慧打算从箱内抽球31次,每次从箱内抽出一球,如果抽出白球则将白球放回箱内,如果抽出红球则不将红球放回箱内。已知小慧在前30次抽球中共抽出红球4次,若她第31次抽球时箱内的每颗球被抽出的可能性相等,则这次她抽出红球的概率为( )
A. B. C. D.
7.如果(2x+m)(x-3)展开后的结果不含x的一次项,则m的值是( )
A.6 B.±6 C.0 D.3
8.如图,点C在∠AOB的OB边上,用尺规作CN∥OA,在作图痕迹中弧FG是( )
A.以点C为圆心,以OD长为半径的弧
B.以点C为圆心,以DM长为半径的弧
C.以点E为圆心,以OD长为半径的弧
D.以点E为圆心,以DM长为半径的弧
9.(2024雅安中考)如图,直线AB,CD交于点O,OE⊥AB于点O,若∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.30°
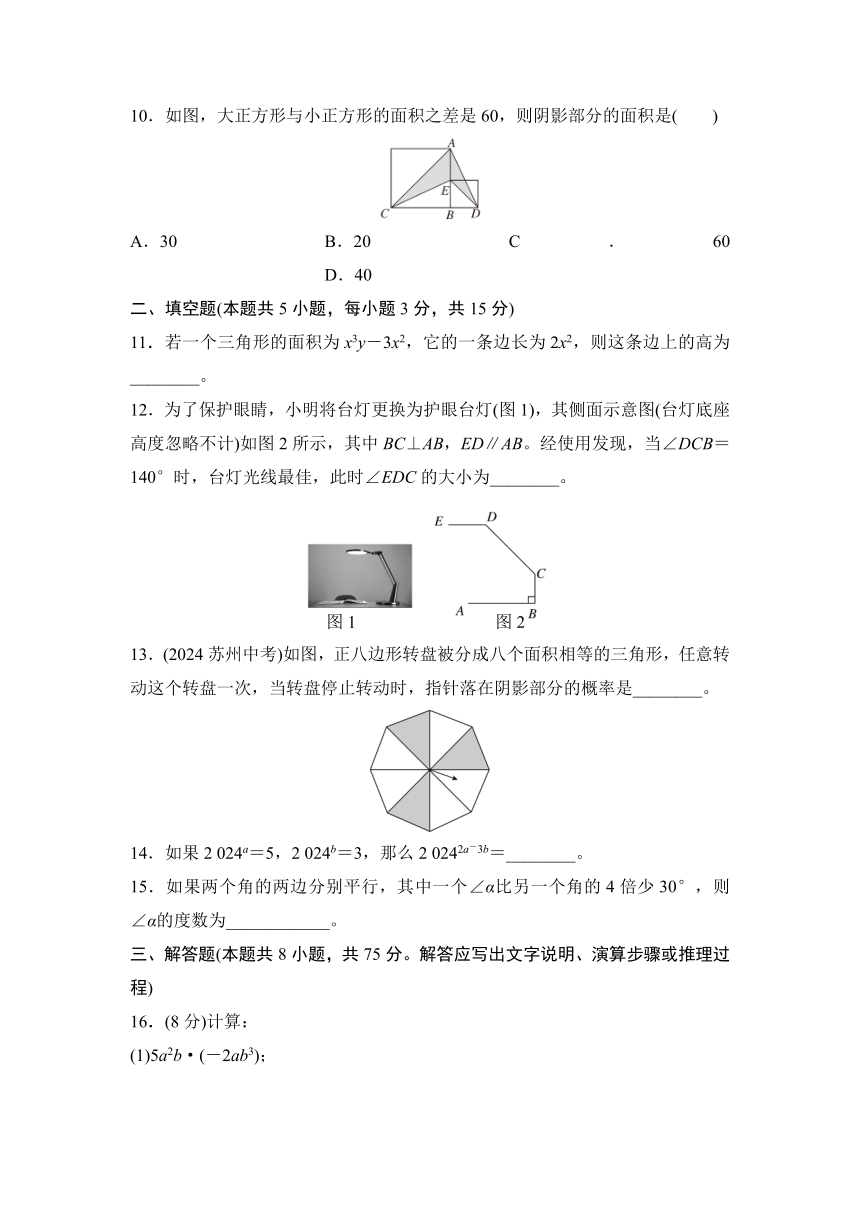
10.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是( )
A.30 B.20 C.60 D.40
二、填空题(本题共5小题,每小题3分,共15分)
11.若一个三角形的面积为x3y-3x2,它的一条边长为2x2,则这条边上的高为________。
12.为了保护眼睛,小明将台灯更换为护眼台灯(图1),其侧面示意图(台灯底座高度忽略不计)如图2所示,其中BC⊥AB,ED∥AB。经使用发现,当∠DCB=140°时,台灯光线最佳,此时∠EDC的大小为________。
13.(2024苏州中考)如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是________。
14.如果2 024a=5,2 024b=3,那么2 0242a-3b=________。
15.如果两个角的两边分别平行,其中一个∠α比另一个角的4倍少30°,则∠α的度数为____________。
三、解答题(本题共8小题,共75分。解答应写出文字说明、演算步骤或推理过程)
16.(8分)计算:
(1)5a2b·(-2ab3);
(2)(2x-3y)2-(y+3x)(3x-y);
(3)x(x2+x-1)-(2x2-1)(x-4);
(4)3b(b-2a3)-(9ab3+12a4b2)÷3ab。
17.(8分)填空:(将下面的过程及依据补充完整)
如图,已知CD平分∠ACB,AC∥DE,CD∥EF。试说明:EF平分∠DEB。
解:因为CD平分∠ACB(已知),
所以∠DCA=∠DCE
(________________)。
因为AC∥DE(已知),
所以∠DCA=______
(__________________________),
所以∠DCE=∠CDE(等量代换)。
因为CD∥EF(已知),
所以________=∠CDE(__________________________),
∠DCE=∠BEF(____________________),
所以________=________(等量代换),
所以EF平分∠DEB(角平分线的判定)。
18.(8分)抛掷一枚质地均匀的骰子(各面上的点数分别为1~6点)1次,落地后:
(1)朝上的点数有哪些结果?他们发生的可能性一样吗?
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件发生的可能性大小相等吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件发生的可能性大小相等吗?如果不相等,那么哪一个发生的可能性大一些?
19.(9分)如图所示,直线AB,CD相交于点O,OM⊥AB。
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD的度数。
20.(9分)先化简,再求值:[(2x+y)2-2x(x-3y)-y2]÷x,其中x=-1,y=-。
21.(10分)如图,这是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠EOF=90°,∠ODC=32°。
(1)求扶手AB与支架OE的夹角∠AOE的度数;
(2)若扶手AB与靠背DM的夹角∠BNM=58°,请对OE∥DM说明理由。
22.(11分)如图,AE平分∠BAC,∠CAE=∠CEA。
(1)如图1,试说明:AB∥CD;
(2)如图2,F为线段AC上一点,连接EF,试说明:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数。(注:三角形三个内角的和等于180°)
23.(12分)将完全平方公式(a+b)2=a2+2ab+b2进行适当的变形,可以解决很多数学问题。例如:若a+b=5,ab=2,求a2+b2的值。解:因为a+b=5,ab=2,所以(a+b)2=25,2ab=4,所以a2+b2+2ab=25,2ab=4,所以a2+b2=21。
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=9,x2+y2=41。
①求xy的值;
②求(x-y)2的值。
(2)若(7-m)(3+m)=12,则(7-m)2+(3+m)2=________。
(3)如图,点C是线段AB上的一点,分别以AC,BC为边作正方形ACDE,BCFG,设正方形ACDE的面积为S1,正方形BCFG的面积为S2,若S1+S2=24,AB=8,求图中阴影部分的面积。
【详解答案】
1.A 解析:A.∠2和∠3是同旁内角,故本选项正确;B.∠1和∠2不是同位角,故本选项错误;C.∠1和∠3是内错角,不是同位角,故本选项错误;D.∠1和∠2不是内错角,故本选项错误。故选A。
2.D 解析:A.a2·a3=a2+3=a5,故本选项不符合题意;B.a12÷a2=a12-2=a10,故本选项不符合题意;C.a3+a3=2a3,故本选项不符合题意;D.(a2)3=a2×3=a6,故本选项符合题意。故选D。
3.A 解析:0.000 92=9.2×10-4。故选A。
4.C 解析:因为AB∥CD,所以∠1=∠DFN=40°,所以∠2=180°-∠DFN=140°。故选C。
5.D 解析:A.当∠5=∠C时,可得AC∥BD,不符合题意;B.当∠1=∠2时,可得AC∥BD,不符合题意;C.由∠B=∠C,不能判定AB∥CE,不符合题意;D.当∠C+∠CAB=180°时,可得AB∥CE,符合题意。故选D。
6.D 解析:因为第31次抽球时箱内共有56个球,其中红球有6个,所以这次她抽出红球的概率为=。故选D。
7.A 解析:(2x+m)(x-3)=2x2+mx-6x-3m=2x2+(m-6)x-3m。因为结果中不含x的一次项,所以m-6=0,解得m=6。故选A。
8.D 解析:由作图可知,弧FG是以点E为圆心,以DM长为半径的弧。故选D。
9.A 解析:因为OE⊥AB,∠1=35°,所以∠AOC=55°,所以∠2=∠AOC=55°。故选A。
10.A 解析:设大正方形的边长为x,小正方形的边长为y,则x2-y2=60。因为三角形AEC和三角形AED有相同的边AE,所以S阴影=(x-y)·(x+y)=(x2-y2)=×60=30。故选A。
11.xy-3 解析:这条边上的高为2(x3y-3x2)÷2x2=(x3y-3x2)÷x2=xy-3。
12.130° 解析:因为BC⊥AB,所以∠B=90°。过点C作CF∥AB,如图。
因为DE∥AB,所以CF∥DE∥AB,
所以∠EDC=180°-∠DCF,
∠BCF=180°-∠B=180°-90°=90°。
因为∠DCF=∠DCB-∠BCF=140°-90°=50°,所以∠EDC=180°-50°=130°。
13. 解析:根据题意可知,正八边形转盘被分成八个面积相等的三角形,其中阴影部分的面积为三个面积相等的三角形的面积之和,所以指针落在阴影部分的概率等于阴影部分的面积除以正八边形的面积,即。
14. 解析:因为2 024a=5,2 024b=3,所以2 0242a-3b=2 0242a÷2 0243b=(2 024a)2÷(2 024b)3=52÷33=。
15.10°或138° 解析:分两种情况:
如图1:
因为AB∥DE,所以∠B=∠1。
因为BC∥EF,所以∠1=∠E,所以∠B=∠E。
如图2:
因为AB∥DE,所以∠B=∠1。
因为BC∥EF,所以∠1+∠E=180°,
所以∠B+∠E=180°。
综上所述,如果两个角的两边分别平行,那么这两个角相等或互补。
设另一个角为x°,
因为∠α比另一个角的4倍少30°,
所以∠α=(4x-30)°,
所以x=4x-30或x+4x-30=180,
解得x=10或x=42。
当x=10时,∠α=(4x-30)°=10°;
当x=42时,∠α=(4x-30)°=138°。
综上所述,∠α的度数为10°或138°。
16.解:(1)原式=-10a2+1b1+3=-10a3b4。
(2)原式=(4x2-12xy+9y2)-(9x2-y2)=-5x2-12xy+10y2。
(3)原式=x3+x2-x-(2x3-8x2-x+4)=x3+x2-x-2x3+8x2+x-4=-x3+9x2-4。
(4)原式=3b2-6a3b-(9ab3÷3ab+12a4b2÷3ab)=3b2-6a3b-3b2-4a3b=-10a3b。
17.解:角平分线的定义 ∠CDE 两直线平行,内错角相等 ∠DEF 两直线平行,内错角相等 两直线平行,同位角相等 ∠DEF ∠BEF
18.解:(1)朝上的点数可能是1,2,3,4,5,6,由于骰子质地均匀,所以它们发生的可能性一样。
(2)因为朝上的点数是奇数有1,3,5共三种情况,朝上的点数是偶数有2,4,6共三种情况,所以这两个事件发生的可能性大小相等。
(3)因为朝上的点数大于4的数有5,6,朝上的点数不大于4的数有1,2,3,4,所以朝上的点数大于4与朝上的点数不大于4发生的可能性大小不相等,朝上的点数不大于4发生的可能性大。
19.解:(1)因为OM⊥AB,∠1=∠2,
所以∠1+∠AOC=∠2+∠AOC=90°,即∠CON=90°。
又因为∠CON+∠NOD=180°,
所以∠NOD=90°。
(2)因为OM⊥AB,∠1=∠BOC,
所以∠BOC=120°,∠1=30°。
又因为∠AOC+∠BOC=180°,
所以∠AOC=60°。
而∠AOC=∠BOD,
所以∠MOD=∠MOB+∠AOC=150°。
20.解:[(2x+y)2-2x(x-3y)-y2]÷x
=[(4x2+4xy+y2-2x2+6xy)-y2]÷x
=(4x2+4xy+y2-2x2+6xy-y2)÷x
=(2x2+10xy)÷x
=2x+10y。
当x=-1,y=-时,
原式=-2-2=-4。
21.解:(1)因为扶手AB与底座CD都平行于地面,
所以AB∥CD,
所以∠NOD=∠ODC=32°,
所以∠AOE=180°-∠EOF-∠NOD=180°-90°-32°=58°。
(2)因为∠BNM=58°,∠AOE=58°,
所以∠AND=∠BNM=58°,
所以∠AOE=∠AND,
所以OE∥DM。
22.解:(1)因为AE平分∠BAC,
所以∠BAE=∠CAE。
因为∠CAE=∠CEA,
所以∠BAE=∠CEA,所以AB∥CD。
(2)如图,过点F作FM∥AB。
因为AB∥CD,所以AB∥FM∥CD。
所以∠BAF+∠AFM=180°,
∠EFM+∠DEF=180°,
所以∠BAF+∠AFM+∠EFM+∠DEF=360°,
即∠BAF+∠AFE+∠DEF=360°。
(3)设∠GEF=∠C=x°。
因为∠GED=2∠GEF,所以∠GED=2x°。
因为AB∥CD,
所以∠C+∠BAC=180°,∠AGE=∠GED=2x°。
所以∠BAC=180°-x°。
因为AE平分∠BAC,
所以∠BAE=∠BAC=(180°-x°)=90°-x°。
又因为AB∥CD,
所以∠BAE+∠AED=180°。
因为∠AEF=35°,
所以∠AEG=∠GEF-∠AEF=x°-35°,
因为∠BAE+∠AEG+∠AGE=180°,
所以90-x+x-35+2x=180,
解得x=50,即∠C=50°。
23.解:(1)①因为(x+y)2-2xy=x2+y2,x+y=9,x2+y2=41,所以92-2xy=41,所以xy=20。
②(x-y)2=(x+y)2-4xy=92-4×20=1。
(2)76 解析:因为(7-m)+(3+m)=10,(7-m)(3+m)=12,所以(7-m)2+(3+m)2=[(7-m)+(3+m)]2-2(7-m)·(3+m)=100-2×12=76。
(3)设AC=m,CF=n,因为AB=8,所以m+n=8。又因为S1+S2=24,所以m2+n2=24。由完全平方公式可得(m+n)2=m2+2mn+n2,所以82=24+2mn,所以mn=20,所以S阴影部分=mn=10。
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,下列说法正确的是( )
A.∠2与∠3是同旁内角
B.∠1与∠2是同位角
C.∠1与∠3是同位角
D.∠1与∠2是内错角
2.(2024烟台中考)下列计算结果为a6的是( )
A.a2·a3 B.a12÷a2
C.a3+a3 D.(a2)3
3.在科幻小说《三体》中,制造太空电梯的材料是由科学家汪淼发明的一种具有超高强度纳米丝的“飞刃”。若“飞刃”的直径为0.000 92 dm,则“飞刃”的直径(dm)可用科学记数法表示为( )
A.9.2×10-4 B.92×10-3
C.0.92×10-3 D.-9.2×104
4.(2024宿迁中考)如图,直线AB∥CD,直线MN分别与直线AB,CD交于点E,F,且∠1=40°,则∠2等于( )
A.120° B.130° C.140° D.150°
5.如图,点E在CD延长线上,下列条件中能判定AB∥CE的是( )
A.∠5=∠C
B.∠1=∠2
C.∠B=∠C
D.∠C+∠CAB=180°
6.箱内有50颗白球和10颗红球,小慧打算从箱内抽球31次,每次从箱内抽出一球,如果抽出白球则将白球放回箱内,如果抽出红球则不将红球放回箱内。已知小慧在前30次抽球中共抽出红球4次,若她第31次抽球时箱内的每颗球被抽出的可能性相等,则这次她抽出红球的概率为( )
A. B. C. D.
7.如果(2x+m)(x-3)展开后的结果不含x的一次项,则m的值是( )
A.6 B.±6 C.0 D.3
8.如图,点C在∠AOB的OB边上,用尺规作CN∥OA,在作图痕迹中弧FG是( )
A.以点C为圆心,以OD长为半径的弧
B.以点C为圆心,以DM长为半径的弧
C.以点E为圆心,以OD长为半径的弧
D.以点E为圆心,以DM长为半径的弧
9.(2024雅安中考)如图,直线AB,CD交于点O,OE⊥AB于点O,若∠1=35°,则∠2的度数是( )
A.55° B.45° C.35° D.30°
10.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是( )
A.30 B.20 C.60 D.40
二、填空题(本题共5小题,每小题3分,共15分)
11.若一个三角形的面积为x3y-3x2,它的一条边长为2x2,则这条边上的高为________。
12.为了保护眼睛,小明将台灯更换为护眼台灯(图1),其侧面示意图(台灯底座高度忽略不计)如图2所示,其中BC⊥AB,ED∥AB。经使用发现,当∠DCB=140°时,台灯光线最佳,此时∠EDC的大小为________。
13.(2024苏州中考)如图,正八边形转盘被分成八个面积相等的三角形,任意转动这个转盘一次,当转盘停止转动时,指针落在阴影部分的概率是________。
14.如果2 024a=5,2 024b=3,那么2 0242a-3b=________。
15.如果两个角的两边分别平行,其中一个∠α比另一个角的4倍少30°,则∠α的度数为____________。
三、解答题(本题共8小题,共75分。解答应写出文字说明、演算步骤或推理过程)
16.(8分)计算:
(1)5a2b·(-2ab3);
(2)(2x-3y)2-(y+3x)(3x-y);
(3)x(x2+x-1)-(2x2-1)(x-4);
(4)3b(b-2a3)-(9ab3+12a4b2)÷3ab。
17.(8分)填空:(将下面的过程及依据补充完整)
如图,已知CD平分∠ACB,AC∥DE,CD∥EF。试说明:EF平分∠DEB。
解:因为CD平分∠ACB(已知),
所以∠DCA=∠DCE
(________________)。
因为AC∥DE(已知),
所以∠DCA=______
(__________________________),
所以∠DCE=∠CDE(等量代换)。
因为CD∥EF(已知),
所以________=∠CDE(__________________________),
∠DCE=∠BEF(____________________),
所以________=________(等量代换),
所以EF平分∠DEB(角平分线的判定)。
18.(8分)抛掷一枚质地均匀的骰子(各面上的点数分别为1~6点)1次,落地后:
(1)朝上的点数有哪些结果?他们发生的可能性一样吗?
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件发生的可能性大小相等吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件发生的可能性大小相等吗?如果不相等,那么哪一个发生的可能性大一些?
19.(9分)如图所示,直线AB,CD相交于点O,OM⊥AB。
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD的度数。
20.(9分)先化简,再求值:[(2x+y)2-2x(x-3y)-y2]÷x,其中x=-1,y=-。
21.(10分)如图,这是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠EOF=90°,∠ODC=32°。
(1)求扶手AB与支架OE的夹角∠AOE的度数;
(2)若扶手AB与靠背DM的夹角∠BNM=58°,请对OE∥DM说明理由。
22.(11分)如图,AE平分∠BAC,∠CAE=∠CEA。
(1)如图1,试说明:AB∥CD;
(2)如图2,F为线段AC上一点,连接EF,试说明:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数。(注:三角形三个内角的和等于180°)
23.(12分)将完全平方公式(a+b)2=a2+2ab+b2进行适当的变形,可以解决很多数学问题。例如:若a+b=5,ab=2,求a2+b2的值。解:因为a+b=5,ab=2,所以(a+b)2=25,2ab=4,所以a2+b2+2ab=25,2ab=4,所以a2+b2=21。
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=9,x2+y2=41。
①求xy的值;
②求(x-y)2的值。
(2)若(7-m)(3+m)=12,则(7-m)2+(3+m)2=________。
(3)如图,点C是线段AB上的一点,分别以AC,BC为边作正方形ACDE,BCFG,设正方形ACDE的面积为S1,正方形BCFG的面积为S2,若S1+S2=24,AB=8,求图中阴影部分的面积。
【详解答案】
1.A 解析:A.∠2和∠3是同旁内角,故本选项正确;B.∠1和∠2不是同位角,故本选项错误;C.∠1和∠3是内错角,不是同位角,故本选项错误;D.∠1和∠2不是内错角,故本选项错误。故选A。
2.D 解析:A.a2·a3=a2+3=a5,故本选项不符合题意;B.a12÷a2=a12-2=a10,故本选项不符合题意;C.a3+a3=2a3,故本选项不符合题意;D.(a2)3=a2×3=a6,故本选项符合题意。故选D。
3.A 解析:0.000 92=9.2×10-4。故选A。
4.C 解析:因为AB∥CD,所以∠1=∠DFN=40°,所以∠2=180°-∠DFN=140°。故选C。
5.D 解析:A.当∠5=∠C时,可得AC∥BD,不符合题意;B.当∠1=∠2时,可得AC∥BD,不符合题意;C.由∠B=∠C,不能判定AB∥CE,不符合题意;D.当∠C+∠CAB=180°时,可得AB∥CE,符合题意。故选D。
6.D 解析:因为第31次抽球时箱内共有56个球,其中红球有6个,所以这次她抽出红球的概率为=。故选D。
7.A 解析:(2x+m)(x-3)=2x2+mx-6x-3m=2x2+(m-6)x-3m。因为结果中不含x的一次项,所以m-6=0,解得m=6。故选A。
8.D 解析:由作图可知,弧FG是以点E为圆心,以DM长为半径的弧。故选D。
9.A 解析:因为OE⊥AB,∠1=35°,所以∠AOC=55°,所以∠2=∠AOC=55°。故选A。
10.A 解析:设大正方形的边长为x,小正方形的边长为y,则x2-y2=60。因为三角形AEC和三角形AED有相同的边AE,所以S阴影=(x-y)·(x+y)=(x2-y2)=×60=30。故选A。
11.xy-3 解析:这条边上的高为2(x3y-3x2)÷2x2=(x3y-3x2)÷x2=xy-3。
12.130° 解析:因为BC⊥AB,所以∠B=90°。过点C作CF∥AB,如图。
因为DE∥AB,所以CF∥DE∥AB,
所以∠EDC=180°-∠DCF,
∠BCF=180°-∠B=180°-90°=90°。
因为∠DCF=∠DCB-∠BCF=140°-90°=50°,所以∠EDC=180°-50°=130°。
13. 解析:根据题意可知,正八边形转盘被分成八个面积相等的三角形,其中阴影部分的面积为三个面积相等的三角形的面积之和,所以指针落在阴影部分的概率等于阴影部分的面积除以正八边形的面积,即。
14. 解析:因为2 024a=5,2 024b=3,所以2 0242a-3b=2 0242a÷2 0243b=(2 024a)2÷(2 024b)3=52÷33=。
15.10°或138° 解析:分两种情况:
如图1:
因为AB∥DE,所以∠B=∠1。
因为BC∥EF,所以∠1=∠E,所以∠B=∠E。
如图2:
因为AB∥DE,所以∠B=∠1。
因为BC∥EF,所以∠1+∠E=180°,
所以∠B+∠E=180°。
综上所述,如果两个角的两边分别平行,那么这两个角相等或互补。
设另一个角为x°,
因为∠α比另一个角的4倍少30°,
所以∠α=(4x-30)°,
所以x=4x-30或x+4x-30=180,
解得x=10或x=42。
当x=10时,∠α=(4x-30)°=10°;
当x=42时,∠α=(4x-30)°=138°。
综上所述,∠α的度数为10°或138°。
16.解:(1)原式=-10a2+1b1+3=-10a3b4。
(2)原式=(4x2-12xy+9y2)-(9x2-y2)=-5x2-12xy+10y2。
(3)原式=x3+x2-x-(2x3-8x2-x+4)=x3+x2-x-2x3+8x2+x-4=-x3+9x2-4。
(4)原式=3b2-6a3b-(9ab3÷3ab+12a4b2÷3ab)=3b2-6a3b-3b2-4a3b=-10a3b。
17.解:角平分线的定义 ∠CDE 两直线平行,内错角相等 ∠DEF 两直线平行,内错角相等 两直线平行,同位角相等 ∠DEF ∠BEF
18.解:(1)朝上的点数可能是1,2,3,4,5,6,由于骰子质地均匀,所以它们发生的可能性一样。
(2)因为朝上的点数是奇数有1,3,5共三种情况,朝上的点数是偶数有2,4,6共三种情况,所以这两个事件发生的可能性大小相等。
(3)因为朝上的点数大于4的数有5,6,朝上的点数不大于4的数有1,2,3,4,所以朝上的点数大于4与朝上的点数不大于4发生的可能性大小不相等,朝上的点数不大于4发生的可能性大。
19.解:(1)因为OM⊥AB,∠1=∠2,
所以∠1+∠AOC=∠2+∠AOC=90°,即∠CON=90°。
又因为∠CON+∠NOD=180°,
所以∠NOD=90°。
(2)因为OM⊥AB,∠1=∠BOC,
所以∠BOC=120°,∠1=30°。
又因为∠AOC+∠BOC=180°,
所以∠AOC=60°。
而∠AOC=∠BOD,
所以∠MOD=∠MOB+∠AOC=150°。
20.解:[(2x+y)2-2x(x-3y)-y2]÷x
=[(4x2+4xy+y2-2x2+6xy)-y2]÷x
=(4x2+4xy+y2-2x2+6xy-y2)÷x
=(2x2+10xy)÷x
=2x+10y。
当x=-1,y=-时,
原式=-2-2=-4。
21.解:(1)因为扶手AB与底座CD都平行于地面,
所以AB∥CD,
所以∠NOD=∠ODC=32°,
所以∠AOE=180°-∠EOF-∠NOD=180°-90°-32°=58°。
(2)因为∠BNM=58°,∠AOE=58°,
所以∠AND=∠BNM=58°,
所以∠AOE=∠AND,
所以OE∥DM。
22.解:(1)因为AE平分∠BAC,
所以∠BAE=∠CAE。
因为∠CAE=∠CEA,
所以∠BAE=∠CEA,所以AB∥CD。
(2)如图,过点F作FM∥AB。
因为AB∥CD,所以AB∥FM∥CD。
所以∠BAF+∠AFM=180°,
∠EFM+∠DEF=180°,
所以∠BAF+∠AFM+∠EFM+∠DEF=360°,
即∠BAF+∠AFE+∠DEF=360°。
(3)设∠GEF=∠C=x°。
因为∠GED=2∠GEF,所以∠GED=2x°。
因为AB∥CD,
所以∠C+∠BAC=180°,∠AGE=∠GED=2x°。
所以∠BAC=180°-x°。
因为AE平分∠BAC,
所以∠BAE=∠BAC=(180°-x°)=90°-x°。
又因为AB∥CD,
所以∠BAE+∠AED=180°。
因为∠AEF=35°,
所以∠AEG=∠GEF-∠AEF=x°-35°,
因为∠BAE+∠AEG+∠AGE=180°,
所以90-x+x-35+2x=180,
解得x=50,即∠C=50°。
23.解:(1)①因为(x+y)2-2xy=x2+y2,x+y=9,x2+y2=41,所以92-2xy=41,所以xy=20。
②(x-y)2=(x+y)2-4xy=92-4×20=1。
(2)76 解析:因为(7-m)+(3+m)=10,(7-m)(3+m)=12,所以(7-m)2+(3+m)2=[(7-m)+(3+m)]2-2(7-m)·(3+m)=100-2×12=76。
(3)设AC=m,CF=n,因为AB=8,所以m+n=8。又因为S1+S2=24,所以m2+n2=24。由完全平方公式可得(m+n)2=m2+2mn+n2,所以82=24+2mn,所以mn=20,所以S阴影部分=mn=10。
同课章节目录
