北师大版数学九年级下册第三章圆单元测试卷
文档属性
| 名称 | 北师大版数学九年级下册第三章圆单元测试卷 |  | |
| 格式 | doc | ||
| 文件大小 | 563.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-04 13:15:01 | ||
图片预览




文档简介
本资料来自于资源21世纪教育网www.21cnjy.com
北师大版数学九年级下册第三章圆单元测试卷原版卷
一.选择题(共12小题)
1.(2015秋 文昌校级期末)下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
A.1个 B.2个 C.3个 D.4个
2.(2015秋 德州校级期中)下列说法正确的个数是( )
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
3.(2016 鄂城区一模)如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,),则四边形ABCD面积最大值为( )
( http: / / www.21cnjy.com )
A.2 B.5 C.4 D.6
4.(2016 大邑县模拟)如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
( http: / / www.21cnjy.com )
A.15° B.30° C.45° D.60°
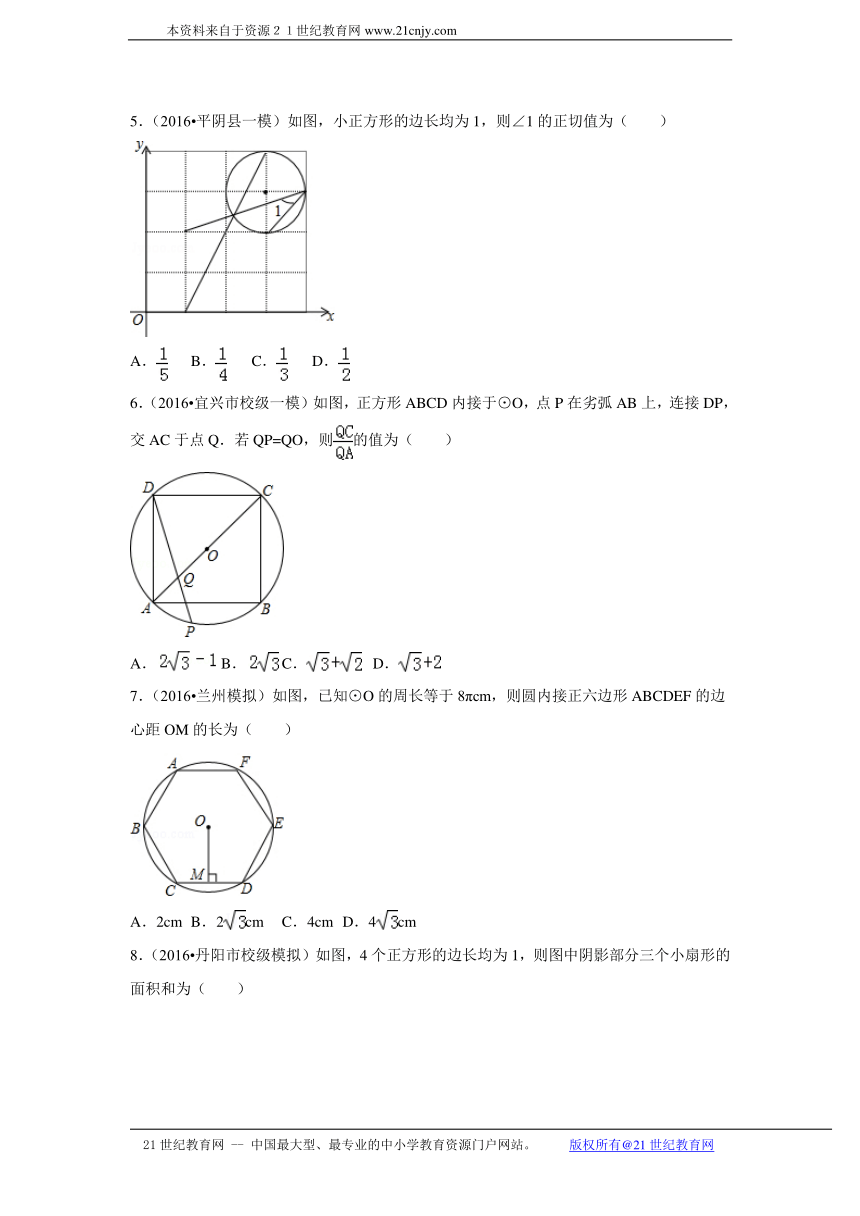
5.(2016 平阴县一模)如图,小正方形的边长均为1,则∠1的正切值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
6.(2016 宜兴市校级一模)如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
7.(2016 兰州模拟)如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
( http: / / www.21cnjy.com )
A.2cm B.2cm C.4cm D.4cm
8.(2016 丹阳市校级模拟)如图,4个正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
( http: / / www.21cnjy.com )
A. B. C. D.
9.(2016 孝义市一模)如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
10.(2016春 盐城校级月考)如图, ( http: / / www.21cnjy.com )在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
( http: / / www.21cnjy.com )
A. B. C. D.
11.(2015 雅安)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:
①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.
其中正确结论的个数是( )
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.5
12.(2015 贺州)如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=BC;④BD=CD,
其中正确的个数为( )
( http: / / www.21cnjy.com )
A.4个 B.3个 C.2个 D.1个
二.填空题(共4小题)
13.(2016 重庆模拟)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= .21·世纪*教育网
( http: / / www.21cnjy.com )
14.(2016 丹东模拟)如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=,则AB= .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
15.(2016 兰州模拟)如图,在直角坐 ( http: / / www.21cnjy.com )标系中,直线AB交x轴、y轴于点A(3,0)与B(0,﹣4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是 .
( http: / / www.21cnjy.com )
16.(2016 苏州模拟)如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016= .
( http: / / www.21cnjy.com )
三.解答题(共5小题)
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
( http: / / www.21cnjy.com )
18.(2016 云南模拟)如图,⊙O的直 ( http: / / www.21cnjy.com )径AB垂直弦CD于E,过点C的切线CF交AB延长线于F,连接CO并延长交AD于G,且CG⊥AD.求证:△CEF≌△DEA.
( http: / / www.21cnjy.com )
19.(2016 天桥区一模)完成下列各题:
(1)如图,在矩形ABCD中,AF=BE,求证:DE=CF;
(2)如图,AB是⊙O的直 ( http: / / www.21cnjy.com )径,CA与⊙O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE,BD,∠ABD=25°,求∠C的度数.
( http: / / www.21cnjy.com )
20.(2016 商水县一模)如图,A ( http: / / www.21cnjy.com )B为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t= 时,四边形AMQN为菱形;当t= 时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
( http: / / www.21cnjy.com )
21.(2016 贵港一模)如图, ( http: / / www.21cnjy.com )在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=,求BE的长.
( http: / / www.21cnjy.com )
北师大版数学九年级下册第三章圆单元测试卷解析卷
一.选择题(共12小题)
1.(2015秋 文昌校级期末)下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①因为直径的两个端点在圆上,直径是连接圆上这两个端点的线段.所以直径是弦是正确的.
②弦是连接圆上两点的线段,如果过圆心就是直径,不过圆心就不是直径.所以弦是直径不正确.
③过圆内一点是有无数多条弦,但这些弦不一定相等,其中过圆心的弦是最长的.所以③不正确.
④直径是过圆心的弦,当然是圆中最长的弦.所以④正确.
故选B.
【分析】弦是连接圆上两点间的线段,直径是弦,是过圆心的弦,是圆中最长的弦.由弦和直径的定义对这四个命题作出判断. www.21-cn-jy.com
2.(2015秋 德州校级期中)下列说法正确的个数是( )
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
【解答】解:直径是圆中最长的弦,所以①正确;
弧不一定是半圆,所以②错误;
过圆心的弦是直径,所以③错误;
半圆是弧,所以④错误;
在同圆或等圆中,长度相等的弧是等弧,所以⑤错误.
故选A.
【分析】根据直径的定义对①③进行判断;根据弧和半圆的定义对②④进行判断;根据等弧的定义对⑤进行判断. 2-1-c-n-j-y
3.(2016 鄂城区一模)如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,),则四边形ABCD面积最大值为( )
( http: / / www.21cnjy.com )
A.2 B.5 C.4 D.6
【解答】解:当AC、BD相等,且OM平分两弦的相交的角时,这时O到弦的距离为:OM×sin45=,21*cnjy*com
由勾股定理及垂径定理知弦长为:,
S=××=5;
故选B.
【分析】解答本题要注意当AC、BD ( http: / / www.21cnjy.com )相等,且OM平分两弦的相交的角时,此时四边形ABCD的面积最大,求出对角线AC、BD的长度可以求得四边形ABCD的最大面积.
4.(2016 大邑县模拟)如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )21教育网
( http: / / www.21cnjy.com )
A.15° B.30° C.45° D.60°
【解答】解:∵OA=AB,OA=OB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠ACB=30°,
故选:B.
【分析】根据题意得到△AOB是等边三角形,求出∠AOB的度数,根据圆周角定理计算即可.
5.(2016 平阴县一模)如图,小正方形的边长均为1,则∠1的正切值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:如图,∵∠1=∠2,
∴tan∠1=tan∠2=.
故选D.
( http: / / www.21cnjy.com )
【分析】首先由圆周角证得∠1=∠2,然后由三角函数的定义,求得答案.
6.(2016 宜兴市校级一模)如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA QC=QP QD.
即(r﹣m)(r+m)=m QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选D.
( http: / / www.21cnjy.com )
【分析】设⊙O的半径为r,QO=m,则QP= ( http: / / www.21cnjy.com )m,QC=r+m,QA=r﹣m.利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值. 【来源:21·世纪·教育·网】
7.(2016 兰州模拟)如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
( http: / / www.21cnjy.com )
A.2cm B.2cm C.4cm D.4cm
【解答】解:连接OC,OD,
∵正六边形ABCDEF是圆的内接多边形,
∴∠COD=60°,
∵OC=OD,OM⊥CD,
∴∠COM=30°,
∵⊙O的周长等于8πcm,
∴OC=4cm,
∴OM=4cos30°=2cm,
故选B.
( http: / / www.21cnjy.com )
【分析】连接OC,OD,由 ( http: / / www.21cnjy.com )正六边形ABCDEF可求出∠COD=60°,进而可求出∠COM=30°,根据30°角的锐角三角函数值即可求出边心距OM的长.
8.(2016 丹阳市校级模拟)如图,4个正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:由观察知三个 ( http: / / www.21cnjy.com )扇形的半径相等均为1,且左边上下两个扇形的圆心角正好是直角三角形的两个锐角,所以它们的和为90°,右上面扇形圆心角的度数为45°,
∴阴影部分的面积应为:S==π.
故选A.
【分析】根据正方形的性质可得出每个扇形的圆心角的度数,从而阴影部分可看成是圆心角为135°,半径为1是扇形,求解即可.
9.(2016 孝义市一模)如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:如图,过点点G作GM⊥AD,垂足为M,
( http: / / www.21cnjy.com )
则四边形GCMD是矩形,
∴GM=CD=1,
又∵AG=AD=2,
∴在RT△AGM中,∠GAM=30°,
则图中阴影部分的面积为:=,
故选:A.
【分析】过点点G作GM⊥AD,垂足为M,在RT△AGM中可知∠GAM=30°,根据扇形面积公式计算即可.
10.(2016春 盐城校级月考)如图 ( http: / / www.21cnjy.com ),在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:连OD,OE,如图,
∴OD⊥AB,OE⊥AC,
∵∠A=90°,OE=OD,
∴四边形OEAD为正方形,
∵AB=AC=2,O为BC的中点,
∴OD=OE=AC=1,
∴S阴影部分=S正方形OEAD﹣S扇形OED=1﹣.
故选A.
( http: / / www.21cnjy.com )
【分析】连OD,OE,根据切线的性质得 ( http: / / www.21cnjy.com )到OD⊥AB,OE⊥AC,则四边形OEAD为正方形,而AB=AC=2,O为BC的中点,则OD=OE=1,再根据正方形的面积公式和扇形的面积公式,利用S阴影部分=S正方形OEAD﹣S扇形OED,进行计算即可.
11.(2015 雅安)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:
①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.
其中正确结论的个数是( )
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.5
【解答】解:∵MN是⊙O的直径,AB⊥MN,
∴AD=BD,=,∠MAN=90°(①②③正确)
∵=,
∴==,
∴∠ACM+∠ANM=∠MOB(④正确)
∵∠MAE=∠AME,
∴AE=ME,∠EAF=∠AFM,
∴AE=EF,
∴AE=MF(⑤正确).
正确的结论共5个.
故选:D.
【分析】根据AB⊥MN,垂径定理得出①③正确,利用MN是直径得出②正确,==,得出④正确,结合②④得出⑤正确即可.
12.(2015 贺州)如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=BC;④BD=CD,
其中正确的个数为( )
( http: / / www.21cnjy.com )
A.4个 B.3个 C.2个 D.1个
【解答】解:连接DO,
∵BC是⊙O的直径,AD是⊙O的切线,切点为D,
∴∠BDC=∠ADO=90°,
∵DO=CO,
∴∠C=∠CDO=30°,
∴∠A=30°,∠DBC=60°,
∠ADB=30°,
∴AD=DC,故①正确;
∵∠A=30°,∠DBC=60°,
∴∠ADB=30°,
∴AB=BD,故②正确;
∵∠C=30°,∠BDC=90°,
∴BD=BC,
∵AB=BD,
∴AB=BC,故③正确;
无法得到BD=CD,故④错误.
故选:B.
( http: / / www.21cnjy.com )
【分析】利用圆周角定理结合切线的性质得出∠BDC=∠ADO=90°,进而得出∠A,∠ADB的度数即可得出答案,再利用直角三角形中30°所对的边等于斜边的一半进而得出AB=BC,判断即可.
二.填空题(共4小题)
13.(2016 重庆模拟)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= 40° .
( http: / / www.21cnjy.com )
【解答】解:连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠D=∠ABC=50°,
∴∠CAD=90°﹣∠D=40°.
故答案为:40°.
( http: / / www.21cnjy.com )
【分析】首先连接CD,由AD是⊙O ( http: / / www.21cnjy.com )的直径,根据直径所对的圆周角是直角,可求得∠ACD=90°,又由圆周角定理,可得∠D=∠ABC=50°,继而求得答案.
14.(2016 丹东模拟)如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=,则AB= . 21*cnjy*com
( http: / / www.21cnjy.com )
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠BDC,
∴tan∠BDC=tanA=,
∵BC=2,
∴AC=2.5,
∴AB==,
故答案为:.
【分析】由圆周角定理可得△ACB是直角三 ( http: / / www.21cnjy.com )角形,∠A=∠BDC,已知tan∠BDC的值,进而可得到tanA的值,则Rt△ACB可解,进而可求出AB的长. 21cnjy.com
15.(2016 兰州模拟)如图,在直角坐标系中,直线AB交x轴、y轴于点A(3,0)与B(0,﹣4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是 <t< .
( http: / / www.21cnjy.com )
【解答】解:如图所示:
∵A(3,0)、B(0,﹣4),
∴OA=3,OB=4,
∴AB==5,
过P点作AB的垂线,垂足为Q,则PQ=1;
①当⊙P在直线AB的左边与直线AB相切时,AP=3﹣t,
则△APQ∽△ABO,
∴,即,
解得:t=;
②当⊙P在直线AB的右边与直线AB相切时,AP=t﹣3;
则△APQ∽△ABO,
∴,即,
解得:t=;
综上所述:动圆与直线AB相切时t的取值是或,
∴动圆与直线AB相交时t的取值范围是<t<.
故答案为:<t<.
( http: / / www.21cnjy.com )
【分析】在Rt△OAB中,OA=3, ( http: / / www.21cnjy.com )OB=4,由勾股定理得AB=5,过P点作AB的垂线,垂足为Q,PQ=1;当⊙O在直线AB的左边与直线AB相切时,AP=3﹣t,根据△APQ∽△ABO中的成比例线段求解;当⊙P在直线AB的右边与直线AB相切时,AP=t﹣3,根据△APQ∽△ABO中的成比例线段求解;得出动圆与直线AB相切时t的取值,即可得出动圆与直线AB相交时t的取值范围. 2·1·c·n·j·y
16.(2016 苏州模拟)如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016= 32015 .21教育名师原创作品
( http: / / www.21cnjy.com )
【解答】解:设A、B、C是切点,由题意直线y=x与x轴的夹角为30°,
在RT△OO1A中,∵AO1=1,∠AOO1=30°,
∴OO1=2AO1=2,
同理:OO2=2BO2,OO3=2CO3,
∴3+r2=2r2,
∴r2=3,
9+r3=2r3,
r3=9,
∴r1=1,r2=3,r3=9…rn=3n﹣1,
∴r2016=32015.
故答案为32015.
( http: / / www.21cnjy.com )
【分析】先求出r1=1,r2=3,r3=9…rn=3n﹣1,根据规律即可解决.
三.解答题(共5小题)
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.【来源:21cnj*y.co*m】
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
( http: / / www.21cnjy.com )
【解答】解:(1)∵AB为直径,点B为的中点,CD=2,
∴AB⊥CD,
∴DE=CD=.
在Rt△ODE中,
∵OD=r,OE=5﹣r,DE=,
∴r2=(5﹣r)2+()2,解得r=3;
(2)∵由(1)知,OE=AE﹣AO=5﹣3=2,
∴tan∠FCE=tan∠DOB==.
在Rt△FCE中,
∵==,
∴EF=,
∴当点F在线段CD的上方时,AF=AE﹣EF=5﹣=;
当点F在线段CD的下方时,AF=AE+EF=5+=>AB,不合题意.
综上所述,AF=.
( http: / / www.21cnjy.com )
【分析】(1)先根据垂径定理得出E为CD的中点,再由勾股定理即可得出结论;
(2)先由锐角三角函数的定义求出EF的长,再分点F在线段CD的上方与下方两种情况进行讨论即可.
18.(2016 云南模拟)如图,⊙O ( http: / / www.21cnjy.com )的直径AB垂直弦CD于E,过点C的切线CF交AB延长线于F,连接CO并延长交AD于G,且CG⊥AD.求证:△CEF≌△DEA.
( http: / / www.21cnjy.com )
【解答】证明:∵CF是⊙O的切线
∴∠OCF=90°,
∴CG⊥CF,
又∵CG⊥AD,
∴CF∥AD,
∴∠ECF=∠EDA,∠F=∠A,
∵直径AB垂直弦CD,
∴CE=DE,
在△CEF和△DEA中,
,
∴△CEF≌△DEA(ASA).
【分析】由CF是⊙O的切线,易 ( http: / / www.21cnjy.com )得CG⊥CF,证得CF∥AD,得出∠ECF=∠EDA,∠F=∠A,根据垂径定理得出CE=DE,然后根据AAS即可证得△CEF≌△DEA.
19.(2016 天桥区一模)完成下列各题:
(1)如图,在矩形ABCD中,AF=BE,求证:DE=CF;
(2)如图,AB是⊙O的直径,CA与⊙ ( http: / / www.21cnjy.com )O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE,BD,∠ABD=25°,求∠C的度数.21世纪教育网版权所有
( http: / / www.21cnjy.com )
【解答】证明:(1)∵矩形ABCD,
∴∠A=∠B、AD=BC,
∵AF=BE,
∴AE=BF,
在△ADE与△BCF中,
,
∴△ADE≌△BCF(SAS).
∴DE=CF;
(2)∵AC是⊙O的切线,
∴∠CAO=90°.
又∠AOC=2∠ABD=50°,
∴∠C=180°﹣∠AOC﹣∠CAO=180°﹣50°﹣90°=40°.
【分析】(1)要证明DE=CF,只要证明△ADE≌△BCF即可.根据全等三角形的判定定理,可以得出结论.21·cn·jy·com
(2)先求出∠EBO,再利用同弧所对的圆心角等于圆周角的2倍,可求出∠AOC,从而求出∠C的度数. 【出处:21教育名师】
20.(2016 商水县一模)如图,AB为 ( http: / / www.21cnjy.com )⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t= 时,四边形AMQN为菱形;当t= 时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
( http: / / www.21cnjy.com )
【解答】解:(1)AP=t,CQ=t,则PQ=5﹣2t,
∵NM⊥AB,
∴PM=PN,
∴当PA=PQ时,四边形AMQN为菱形,即t=5﹣2t,解得t=;
当∠ONQ=90°时,NQ与⊙O相切,如图,
( http: / / www.21cnjy.com )
OP=t﹣1,OQ=AC﹣OA﹣QC=5﹣1﹣t=4﹣t,
∵∠NOP=∠QON,
∴Rt△ONP∽Rt△OQN,
∴=,即=,
整理得t2﹣5t+5=0,解得t1=,t2=(1≤t≤2.5,故舍去),
即当t=时,NQ与⊙O相切;
故答案为,;
(2)当AC的长为3时,存在t=1,使四边形AMQN为正方形.理由如下:
∵四边形AMQN为正方形.
∴∠MAN=90°,
∴MN为⊙O的直径,
而∠MQN=90°,
∴点Q在⊙O上,
∴AQ为直径,
∴点P在圆心,
∴MN=AQ=2,AP=1,
∴t=AP=1,CQ=t=1,
∴AC=AQ+CQ=2+1=3.
【分析】(1)AP=t,CQ ( http: / / www.21cnjy.com )=t,则PQ=5﹣2t,由于NM⊥AB,根据垂径定理得PM=PN,根据菱形的判定方法,当PA=PQ时,四边形AMQN为菱形,即t=5﹣2t,然后解一元一次方程可求t的值;根据切线的判定定理,当∠ONQ=90°时,NQ与⊙O相切,如图,此时OP=t﹣1,OQ=AC﹣OA﹣QC=4﹣t,再证明Rt△ONP∽Rt△OQN,利用相似比可得t2﹣5t+5=0,然后解一元二次方程可得到t的值;
(2)当四边形AMQN为正方形.则∠M ( http: / / www.21cnjy.com )AN=90°,根据圆周角定理得到MN为⊙O的直径,而∠MQN=90°,又可判断AQ为直径,于是得到点P在圆心,所以t=AP=1,CQ=t=1,则可得到此时AC=AQ+CQ=3.
21.(2016 贵港一模)如图,在R ( http: / / www.21cnjy.com )t△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=,求BE的长.
( http: / / www.21cnjy.com )
【解答】(1)证明:连接DO,如图1所示
∵BD是∠ABC的平分线,
∴∠1=∠2,
∵OB=OD,
∴∠2=∠3,
∴∠1=∠3,
∴DO∥BC,
∵∠C=90°,
∴∠ADO=90°,
即AC⊥OD,
∴AC是⊙O的切线.
(2)解:设⊙O的半径为R,
在Rt△ABC中,∠ACB=90°,sin∠BAC==,
∴BC=×6=4,
由(1)知,OD∥BC,
∴△AOD∽△ABC,
∴,
∴,
解得:R=2.4,过O作OF⊥BC于F,如图所示:
则BE=2BF,OF∥AC,
∴∠BOF=∠BAC,
∴=sin∠BOF=,
∴BF=×2.4=1.6,
∴BE=2BF=3.2.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【分析】(1)连接DO,由等腰三角形的性 ( http: / / www.21cnjy.com )质和角平分线的定义得出∠1=∠3,证出DO∥BC,由平行线的性质得出∠ADO=90°,即可得出结论;
(2)设⊙O的半径为R,由三角函数求出BC, ( http: / / www.21cnjy.com )由平行线得出△AOD∽△ABC,得出对应边成比例,求出半径OD,过O作OF⊥BC于F,则BE=2BF,如图所示:则OF∥AC,由平行线的性质得出∠BOF=∠BAC,由三角函数求出BF,即可得出结果.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
北师大版数学九年级下册第三章圆单元测试卷原版卷
一.选择题(共12小题)
1.(2015秋 文昌校级期末)下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
A.1个 B.2个 C.3个 D.4个
2.(2015秋 德州校级期中)下列说法正确的个数是( )
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
3.(2016 鄂城区一模)如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,),则四边形ABCD面积最大值为( )
( http: / / www.21cnjy.com )
A.2 B.5 C.4 D.6
4.(2016 大邑县模拟)如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
( http: / / www.21cnjy.com )
A.15° B.30° C.45° D.60°
5.(2016 平阴县一模)如图,小正方形的边长均为1,则∠1的正切值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
6.(2016 宜兴市校级一模)如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
7.(2016 兰州模拟)如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
( http: / / www.21cnjy.com )
A.2cm B.2cm C.4cm D.4cm
8.(2016 丹阳市校级模拟)如图,4个正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
( http: / / www.21cnjy.com )
A. B. C. D.
9.(2016 孝义市一模)如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
10.(2016春 盐城校级月考)如图, ( http: / / www.21cnjy.com )在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
( http: / / www.21cnjy.com )
A. B. C. D.
11.(2015 雅安)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:
①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.
其中正确结论的个数是( )
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.5
12.(2015 贺州)如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=BC;④BD=CD,
其中正确的个数为( )
( http: / / www.21cnjy.com )
A.4个 B.3个 C.2个 D.1个
二.填空题(共4小题)
13.(2016 重庆模拟)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= .21·世纪*教育网
( http: / / www.21cnjy.com )
14.(2016 丹东模拟)如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=,则AB= .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
15.(2016 兰州模拟)如图,在直角坐 ( http: / / www.21cnjy.com )标系中,直线AB交x轴、y轴于点A(3,0)与B(0,﹣4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是 .
( http: / / www.21cnjy.com )
16.(2016 苏州模拟)如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016= .
( http: / / www.21cnjy.com )
三.解答题(共5小题)
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
( http: / / www.21cnjy.com )
18.(2016 云南模拟)如图,⊙O的直 ( http: / / www.21cnjy.com )径AB垂直弦CD于E,过点C的切线CF交AB延长线于F,连接CO并延长交AD于G,且CG⊥AD.求证:△CEF≌△DEA.
( http: / / www.21cnjy.com )
19.(2016 天桥区一模)完成下列各题:
(1)如图,在矩形ABCD中,AF=BE,求证:DE=CF;
(2)如图,AB是⊙O的直 ( http: / / www.21cnjy.com )径,CA与⊙O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE,BD,∠ABD=25°,求∠C的度数.
( http: / / www.21cnjy.com )
20.(2016 商水县一模)如图,A ( http: / / www.21cnjy.com )B为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t= 时,四边形AMQN为菱形;当t= 时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
( http: / / www.21cnjy.com )
21.(2016 贵港一模)如图, ( http: / / www.21cnjy.com )在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=,求BE的长.
( http: / / www.21cnjy.com )
北师大版数学九年级下册第三章圆单元测试卷解析卷
一.选择题(共12小题)
1.(2015秋 文昌校级期末)下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①因为直径的两个端点在圆上,直径是连接圆上这两个端点的线段.所以直径是弦是正确的.
②弦是连接圆上两点的线段,如果过圆心就是直径,不过圆心就不是直径.所以弦是直径不正确.
③过圆内一点是有无数多条弦,但这些弦不一定相等,其中过圆心的弦是最长的.所以③不正确.
④直径是过圆心的弦,当然是圆中最长的弦.所以④正确.
故选B.
【分析】弦是连接圆上两点间的线段,直径是弦,是过圆心的弦,是圆中最长的弦.由弦和直径的定义对这四个命题作出判断. www.21-cn-jy.com
2.(2015秋 德州校级期中)下列说法正确的个数是( )
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
【解答】解:直径是圆中最长的弦,所以①正确;
弧不一定是半圆,所以②错误;
过圆心的弦是直径,所以③错误;
半圆是弧,所以④错误;
在同圆或等圆中,长度相等的弧是等弧,所以⑤错误.
故选A.
【分析】根据直径的定义对①③进行判断;根据弧和半圆的定义对②④进行判断;根据等弧的定义对⑤进行判断. 2-1-c-n-j-y
3.(2016 鄂城区一模)如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,),则四边形ABCD面积最大值为( )
( http: / / www.21cnjy.com )
A.2 B.5 C.4 D.6
【解答】解:当AC、BD相等,且OM平分两弦的相交的角时,这时O到弦的距离为:OM×sin45=,21*cnjy*com
由勾股定理及垂径定理知弦长为:,
S=××=5;
故选B.
【分析】解答本题要注意当AC、BD ( http: / / www.21cnjy.com )相等,且OM平分两弦的相交的角时,此时四边形ABCD的面积最大,求出对角线AC、BD的长度可以求得四边形ABCD的最大面积.
4.(2016 大邑县模拟)如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )21教育网
( http: / / www.21cnjy.com )
A.15° B.30° C.45° D.60°
【解答】解:∵OA=AB,OA=OB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠ACB=30°,
故选:B.
【分析】根据题意得到△AOB是等边三角形,求出∠AOB的度数,根据圆周角定理计算即可.
5.(2016 平阴县一模)如图,小正方形的边长均为1,则∠1的正切值为( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:如图,∵∠1=∠2,
∴tan∠1=tan∠2=.
故选D.
( http: / / www.21cnjy.com )
【分析】首先由圆周角证得∠1=∠2,然后由三角函数的定义,求得答案.
6.(2016 宜兴市校级一模)如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )【版权所有:21教育】
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA QC=QP QD.
即(r﹣m)(r+m)=m QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选D.
( http: / / www.21cnjy.com )
【分析】设⊙O的半径为r,QO=m,则QP= ( http: / / www.21cnjy.com )m,QC=r+m,QA=r﹣m.利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值. 【来源:21·世纪·教育·网】
7.(2016 兰州模拟)如图,已知⊙O的周长等于8πcm,则圆内接正六边形ABCDEF的边心距OM的长为( )
( http: / / www.21cnjy.com )
A.2cm B.2cm C.4cm D.4cm
【解答】解:连接OC,OD,
∵正六边形ABCDEF是圆的内接多边形,
∴∠COD=60°,
∵OC=OD,OM⊥CD,
∴∠COM=30°,
∵⊙O的周长等于8πcm,
∴OC=4cm,
∴OM=4cos30°=2cm,
故选B.
( http: / / www.21cnjy.com )
【分析】连接OC,OD,由 ( http: / / www.21cnjy.com )正六边形ABCDEF可求出∠COD=60°,进而可求出∠COM=30°,根据30°角的锐角三角函数值即可求出边心距OM的长.
8.(2016 丹阳市校级模拟)如图,4个正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:由观察知三个 ( http: / / www.21cnjy.com )扇形的半径相等均为1,且左边上下两个扇形的圆心角正好是直角三角形的两个锐角,所以它们的和为90°,右上面扇形圆心角的度数为45°,
∴阴影部分的面积应为:S==π.
故选A.
【分析】根据正方形的性质可得出每个扇形的圆心角的度数,从而阴影部分可看成是圆心角为135°,半径为1是扇形,求解即可.
9.(2016 孝义市一模)如图,两个小正方形的边长都是1,以A为圆心,AD为半径作弧交BC于点G,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:如图,过点点G作GM⊥AD,垂足为M,
( http: / / www.21cnjy.com )
则四边形GCMD是矩形,
∴GM=CD=1,
又∵AG=AD=2,
∴在RT△AGM中,∠GAM=30°,
则图中阴影部分的面积为:=,
故选:A.
【分析】过点点G作GM⊥AD,垂足为M,在RT△AGM中可知∠GAM=30°,根据扇形面积公式计算即可.
10.(2016春 盐城校级月考)如图 ( http: / / www.21cnjy.com ),在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
( http: / / www.21cnjy.com )
A. B. C. D.
【解答】解:连OD,OE,如图,
∴OD⊥AB,OE⊥AC,
∵∠A=90°,OE=OD,
∴四边形OEAD为正方形,
∵AB=AC=2,O为BC的中点,
∴OD=OE=AC=1,
∴S阴影部分=S正方形OEAD﹣S扇形OED=1﹣.
故选A.
( http: / / www.21cnjy.com )
【分析】连OD,OE,根据切线的性质得 ( http: / / www.21cnjy.com )到OD⊥AB,OE⊥AC,则四边形OEAD为正方形,而AB=AC=2,O为BC的中点,则OD=OE=1,再根据正方形的面积公式和扇形的面积公式,利用S阴影部分=S正方形OEAD﹣S扇形OED,进行计算即可.
11.(2015 雅安)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为上一点,且=,连接CM,交AB于点E,交AN于点F,现给出以下结论:
①AD=BD;②∠MAN=90°;③=;④∠ACM+∠ANM=∠MOB;⑤AE=MF.
其中正确结论的个数是( )
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.5
【解答】解:∵MN是⊙O的直径,AB⊥MN,
∴AD=BD,=,∠MAN=90°(①②③正确)
∵=,
∴==,
∴∠ACM+∠ANM=∠MOB(④正确)
∵∠MAE=∠AME,
∴AE=ME,∠EAF=∠AFM,
∴AE=EF,
∴AE=MF(⑤正确).
正确的结论共5个.
故选:D.
【分析】根据AB⊥MN,垂径定理得出①③正确,利用MN是直径得出②正确,==,得出④正确,结合②④得出⑤正确即可.
12.(2015 贺州)如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB=BC;④BD=CD,
其中正确的个数为( )
( http: / / www.21cnjy.com )
A.4个 B.3个 C.2个 D.1个
【解答】解:连接DO,
∵BC是⊙O的直径,AD是⊙O的切线,切点为D,
∴∠BDC=∠ADO=90°,
∵DO=CO,
∴∠C=∠CDO=30°,
∴∠A=30°,∠DBC=60°,
∠ADB=30°,
∴AD=DC,故①正确;
∵∠A=30°,∠DBC=60°,
∴∠ADB=30°,
∴AB=BD,故②正确;
∵∠C=30°,∠BDC=90°,
∴BD=BC,
∵AB=BD,
∴AB=BC,故③正确;
无法得到BD=CD,故④错误.
故选:B.
( http: / / www.21cnjy.com )
【分析】利用圆周角定理结合切线的性质得出∠BDC=∠ADO=90°,进而得出∠A,∠ADB的度数即可得出答案,再利用直角三角形中30°所对的边等于斜边的一半进而得出AB=BC,判断即可.
二.填空题(共4小题)
13.(2016 重庆模拟)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= 40° .
( http: / / www.21cnjy.com )
【解答】解:连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠D=∠ABC=50°,
∴∠CAD=90°﹣∠D=40°.
故答案为:40°.
( http: / / www.21cnjy.com )
【分析】首先连接CD,由AD是⊙O ( http: / / www.21cnjy.com )的直径,根据直径所对的圆周角是直角,可求得∠ACD=90°,又由圆周角定理,可得∠D=∠ABC=50°,继而求得答案.
14.(2016 丹东模拟)如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=,则AB= . 21*cnjy*com
( http: / / www.21cnjy.com )
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠BDC,
∴tan∠BDC=tanA=,
∵BC=2,
∴AC=2.5,
∴AB==,
故答案为:.
【分析】由圆周角定理可得△ACB是直角三 ( http: / / www.21cnjy.com )角形,∠A=∠BDC,已知tan∠BDC的值,进而可得到tanA的值,则Rt△ACB可解,进而可求出AB的长. 21cnjy.com
15.(2016 兰州模拟)如图,在直角坐标系中,直线AB交x轴、y轴于点A(3,0)与B(0,﹣4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是 <t< .
( http: / / www.21cnjy.com )
【解答】解:如图所示:
∵A(3,0)、B(0,﹣4),
∴OA=3,OB=4,
∴AB==5,
过P点作AB的垂线,垂足为Q,则PQ=1;
①当⊙P在直线AB的左边与直线AB相切时,AP=3﹣t,
则△APQ∽△ABO,
∴,即,
解得:t=;
②当⊙P在直线AB的右边与直线AB相切时,AP=t﹣3;
则△APQ∽△ABO,
∴,即,
解得:t=;
综上所述:动圆与直线AB相切时t的取值是或,
∴动圆与直线AB相交时t的取值范围是<t<.
故答案为:<t<.
( http: / / www.21cnjy.com )
【分析】在Rt△OAB中,OA=3, ( http: / / www.21cnjy.com )OB=4,由勾股定理得AB=5,过P点作AB的垂线,垂足为Q,PQ=1;当⊙O在直线AB的左边与直线AB相切时,AP=3﹣t,根据△APQ∽△ABO中的成比例线段求解;当⊙P在直线AB的右边与直线AB相切时,AP=t﹣3,根据△APQ∽△ABO中的成比例线段求解;得出动圆与直线AB相切时t的取值,即可得出动圆与直线AB相交时t的取值范围. 2·1·c·n·j·y
16.(2016 苏州模拟)如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016= 32015 .21教育名师原创作品
( http: / / www.21cnjy.com )
【解答】解:设A、B、C是切点,由题意直线y=x与x轴的夹角为30°,
在RT△OO1A中,∵AO1=1,∠AOO1=30°,
∴OO1=2AO1=2,
同理:OO2=2BO2,OO3=2CO3,
∴3+r2=2r2,
∴r2=3,
9+r3=2r3,
r3=9,
∴r1=1,r2=3,r3=9…rn=3n﹣1,
∴r2016=32015.
故答案为32015.
( http: / / www.21cnjy.com )
【分析】先求出r1=1,r2=3,r3=9…rn=3n﹣1,根据规律即可解决.
三.解答题(共5小题)
17.(2016 奉贤区一模)如图,在⊙O中,AB为直径,点B为的中点,直径AB交弦CD于E,CD=2,AE=5.【来源:21cnj*y.co*m】
(1)求⊙O半径r的值;
(2)点F在直径AB上,连接CF,当∠FCD=∠DOB时,求AF的长.
( http: / / www.21cnjy.com )
【解答】解:(1)∵AB为直径,点B为的中点,CD=2,
∴AB⊥CD,
∴DE=CD=.
在Rt△ODE中,
∵OD=r,OE=5﹣r,DE=,
∴r2=(5﹣r)2+()2,解得r=3;
(2)∵由(1)知,OE=AE﹣AO=5﹣3=2,
∴tan∠FCE=tan∠DOB==.
在Rt△FCE中,
∵==,
∴EF=,
∴当点F在线段CD的上方时,AF=AE﹣EF=5﹣=;
当点F在线段CD的下方时,AF=AE+EF=5+=>AB,不合题意.
综上所述,AF=.
( http: / / www.21cnjy.com )
【分析】(1)先根据垂径定理得出E为CD的中点,再由勾股定理即可得出结论;
(2)先由锐角三角函数的定义求出EF的长,再分点F在线段CD的上方与下方两种情况进行讨论即可.
18.(2016 云南模拟)如图,⊙O ( http: / / www.21cnjy.com )的直径AB垂直弦CD于E,过点C的切线CF交AB延长线于F,连接CO并延长交AD于G,且CG⊥AD.求证:△CEF≌△DEA.
( http: / / www.21cnjy.com )
【解答】证明:∵CF是⊙O的切线
∴∠OCF=90°,
∴CG⊥CF,
又∵CG⊥AD,
∴CF∥AD,
∴∠ECF=∠EDA,∠F=∠A,
∵直径AB垂直弦CD,
∴CE=DE,
在△CEF和△DEA中,
,
∴△CEF≌△DEA(ASA).
【分析】由CF是⊙O的切线,易 ( http: / / www.21cnjy.com )得CG⊥CF,证得CF∥AD,得出∠ECF=∠EDA,∠F=∠A,根据垂径定理得出CE=DE,然后根据AAS即可证得△CEF≌△DEA.
19.(2016 天桥区一模)完成下列各题:
(1)如图,在矩形ABCD中,AF=BE,求证:DE=CF;
(2)如图,AB是⊙O的直径,CA与⊙ ( http: / / www.21cnjy.com )O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE,BD,∠ABD=25°,求∠C的度数.21世纪教育网版权所有
( http: / / www.21cnjy.com )
【解答】证明:(1)∵矩形ABCD,
∴∠A=∠B、AD=BC,
∵AF=BE,
∴AE=BF,
在△ADE与△BCF中,
,
∴△ADE≌△BCF(SAS).
∴DE=CF;
(2)∵AC是⊙O的切线,
∴∠CAO=90°.
又∠AOC=2∠ABD=50°,
∴∠C=180°﹣∠AOC﹣∠CAO=180°﹣50°﹣90°=40°.
【分析】(1)要证明DE=CF,只要证明△ADE≌△BCF即可.根据全等三角形的判定定理,可以得出结论.21·cn·jy·com
(2)先求出∠EBO,再利用同弧所对的圆心角等于圆周角的2倍,可求出∠AOC,从而求出∠C的度数. 【出处:21教育名师】
20.(2016 商水县一模)如图,AB为 ( http: / / www.21cnjy.com )⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t= 时,四边形AMQN为菱形;当t= 时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
( http: / / www.21cnjy.com )
【解答】解:(1)AP=t,CQ=t,则PQ=5﹣2t,
∵NM⊥AB,
∴PM=PN,
∴当PA=PQ时,四边形AMQN为菱形,即t=5﹣2t,解得t=;
当∠ONQ=90°时,NQ与⊙O相切,如图,
( http: / / www.21cnjy.com )
OP=t﹣1,OQ=AC﹣OA﹣QC=5﹣1﹣t=4﹣t,
∵∠NOP=∠QON,
∴Rt△ONP∽Rt△OQN,
∴=,即=,
整理得t2﹣5t+5=0,解得t1=,t2=(1≤t≤2.5,故舍去),
即当t=时,NQ与⊙O相切;
故答案为,;
(2)当AC的长为3时,存在t=1,使四边形AMQN为正方形.理由如下:
∵四边形AMQN为正方形.
∴∠MAN=90°,
∴MN为⊙O的直径,
而∠MQN=90°,
∴点Q在⊙O上,
∴AQ为直径,
∴点P在圆心,
∴MN=AQ=2,AP=1,
∴t=AP=1,CQ=t=1,
∴AC=AQ+CQ=2+1=3.
【分析】(1)AP=t,CQ ( http: / / www.21cnjy.com )=t,则PQ=5﹣2t,由于NM⊥AB,根据垂径定理得PM=PN,根据菱形的判定方法,当PA=PQ时,四边形AMQN为菱形,即t=5﹣2t,然后解一元一次方程可求t的值;根据切线的判定定理,当∠ONQ=90°时,NQ与⊙O相切,如图,此时OP=t﹣1,OQ=AC﹣OA﹣QC=4﹣t,再证明Rt△ONP∽Rt△OQN,利用相似比可得t2﹣5t+5=0,然后解一元二次方程可得到t的值;
(2)当四边形AMQN为正方形.则∠M ( http: / / www.21cnjy.com )AN=90°,根据圆周角定理得到MN为⊙O的直径,而∠MQN=90°,又可判断AQ为直径,于是得到点P在圆心,所以t=AP=1,CQ=t=1,则可得到此时AC=AQ+CQ=3.
21.(2016 贵港一模)如图,在R ( http: / / www.21cnjy.com )t△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AC上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=,求BE的长.
( http: / / www.21cnjy.com )
【解答】(1)证明:连接DO,如图1所示
∵BD是∠ABC的平分线,
∴∠1=∠2,
∵OB=OD,
∴∠2=∠3,
∴∠1=∠3,
∴DO∥BC,
∵∠C=90°,
∴∠ADO=90°,
即AC⊥OD,
∴AC是⊙O的切线.
(2)解:设⊙O的半径为R,
在Rt△ABC中,∠ACB=90°,sin∠BAC==,
∴BC=×6=4,
由(1)知,OD∥BC,
∴△AOD∽△ABC,
∴,
∴,
解得:R=2.4,过O作OF⊥BC于F,如图所示:
则BE=2BF,OF∥AC,
∴∠BOF=∠BAC,
∴=sin∠BOF=,
∴BF=×2.4=1.6,
∴BE=2BF=3.2.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【分析】(1)连接DO,由等腰三角形的性 ( http: / / www.21cnjy.com )质和角平分线的定义得出∠1=∠3,证出DO∥BC,由平行线的性质得出∠ADO=90°,即可得出结论;
(2)设⊙O的半径为R,由三角函数求出BC, ( http: / / www.21cnjy.com )由平行线得出△AOD∽△ABC,得出对应边成比例,求出半径OD,过O作OF⊥BC于F,则BE=2BF,如图所示:则OF∥AC,由平行线的性质得出∠BOF=∠BAC,由三角函数求出BF,即可得出结果.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
