北师大版六年级下册数学图形与几何(课件)(共52张PPT)
文档属性
| 名称 | 北师大版六年级下册数学图形与几何(课件)(共52张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-20 21:05:20 | ||
图片预览











文档简介
(共52张PPT)
图
形
与
几
何
多边形的面积
长方体和正方体
圆
圆柱圆锥
总复习
1
2
3
4
总复习——图形与几何
第 1 课时
多边形的面积
平行四边形
平行四边形的面积=底×高
字母表示:S=ah
平行四边形的底=平行四边形的面积÷平行四边形的高
字母表示:a=S÷h
1
平行四边形的高=平行四边形的面积÷平行四边形的底
字母表示:h=S÷a
知识点
三角形
三角形的面积=底×高÷2
字母表示:S=ah÷2
三角形的底=三角形的面积×2÷三角形的高
字母表示:a =2S÷h
2
三角形的高=三角形的面积×2÷三角形的底
字母表示:h =2S÷a
知识点
梯形
梯形的面积=(上底+下底)×高÷2
字母表示:S=(a+b)×h÷2
梯形的上底=梯形的面积×2÷梯形的高-下底
字母表示:a=2S÷h-b
3
梯形的下底=梯形的面积×2÷梯形的高-上底
字母表示:b=2S÷h-a
知识点
梯形的高=梯形的面积×2÷梯形的上底+下底之和
字母表示:h =2S÷(a+b)
1.一块平行四边形钢板的面积是1391平方米,底是21.4米,它的高是多少米
1391÷21.4=65(米)
答:它的高是65米。
常考题
2.一块平行四边形街头广告牌,底是8.5m,高是5.4m。要粉刷这块广告牌,每平方米要用油漆0.5kg,至少需要准备多少千克油漆?
8.5×5.4×0.5=22.95(kg)
答:至少需要准备22.95千克油漆。
常考题
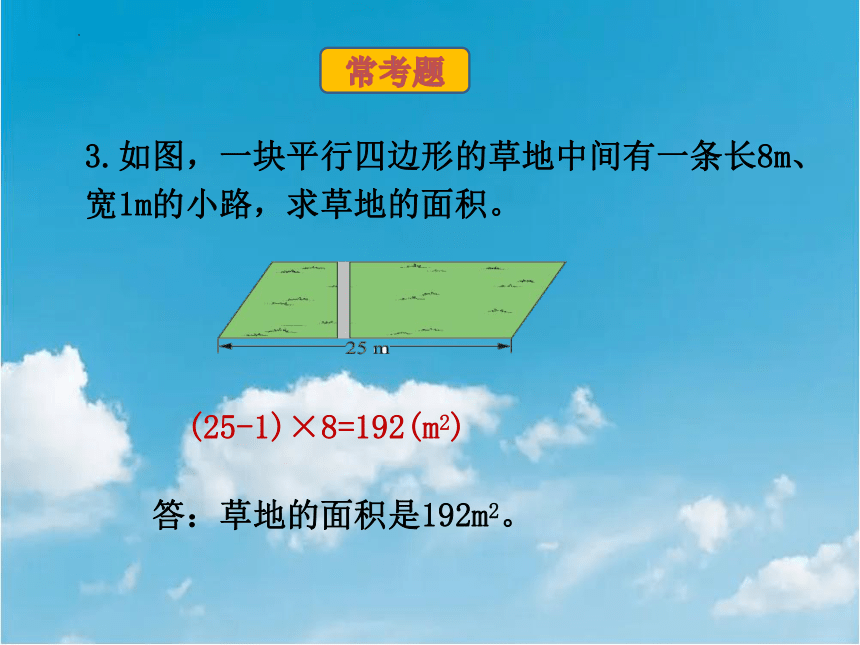
3.如图,一块平行四边形的草地中间有一条长8m、宽1m的小路,求草地的面积。
(25-1)×8=192(m2)
答:草地的面积是192m2。
常考题
4.填空。
(1)一个平行四边形的面积是48平方米,与它等底等高的三角形的面积是( )平方米。
(2)一个三角形和一个平行四边形等底等高,平行四边形的面积与三角形的面积和是27平方厘米,这个三角形的面积是( )平方厘米。
常考题
24
9
5.一个三角形的面积是12.6平方米,底是3米, 这个三角形的高是多少米
12.6×2÷3=8.4(米)
答:这个三角形的高是8.4米。
常考题
6.已知一个三角形的鱼池底是50米,高是40米,它的面积是多少平方米 如果每平方米可养鱼20条,那么这个鱼池总共可养鱼多少条?
50×40÷2×20=20000(条)
答:这个鱼池共可以养20000条鱼。
常考题
7.判断。(对的打“√”,错的打“ ”)
(1)梯形的面积等于平行四边形面积的一半。
( )
常考题
(2)两个完全一样的直角梯形,可以拼成一个 长方形。 ( )
(3)一个上底是5厘米、下底是8厘米、高是3厘米的梯形,它的面积是12平方厘米。( )
√
8.一块梯形花园,上底是35米,下底是25米,面积是1140平方米,高是多少米
1140×2÷(35+25)=38(米)
答:高是38米。
常考题
总复习——图形与几何
第 2 课时
长方体和正方体
长方体和正方体的特点
顶点 个数
面 个数
形状
大小关系
棱 条数
长度关系
8个
8个
6个
6个
正方形
长方形或正方形
大小相同
相对的两个面大小相同
12条
12条
长度相等
相对的棱长度相等
知识点
1
长方体和正方体的棱长总和
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
2
3
长方体的表面积=(长×宽+长×高+宽×高)×2
长方体和正方体的表面积
正方体的表面积=棱长×棱长×6
4
长方体和正方体的体积
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
5
体积与容积的区别
体积是指物体所占空间的大小。
容积是指容器所容纳物体的体积。
6
体积单位:立方米(m3)、立方分米(dm3)、
立方厘米(cm3)
常用的体积单位与容积单位
容积单位:升(L)、毫升(mL)
单位转化方法:大换小用乘法,小换大用除法
7
不规则物体的体积
不规则物体的体积=底面积×水面上升的高度
1.右图是一个长方体盒子相交于同一个顶点的三条棱,它的棱长总和是( )厘米,表面积是( )平方厘米,体积( )立方厘米。
60
148
120
4cm
6cm
5cm
常考题
2.把一根96厘米长的铁丝做成一个长方体框架,长10厘米,宽8厘米,高是( )厘米。
6
3.做两个无盖的长方体水箱,水箱的底面是边长为
3.5dm的正方形,高为4dm,做这两个水箱至少要
用多少平方分米的铁皮?
(3.5×4×4+3.5×3.5)×2
=68.25×2
答:做这对水箱至少要用136.5平方分米的铁皮。
=136.5(平方分米)
常考题
3
正方体棱长扩大几倍,棱长总和就扩大几倍,表面积扩大平方倍,体积扩大立方倍。
4.一个长方体的长、宽、高各扩大到原来3倍,它的棱长总和扩大到原来的( )倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
9
27
长方体长、宽、高扩大几倍,棱长总和就扩大几倍,表面积扩大平方倍,体积扩大立方倍。
常考题
A
5.把一个长方体分成几个小长方体后,小长方体
的体积和原长方体的体积相比较,( )。
A.不变 B.比原来小了
C.比原来大了 D.无法确定
常考题
6.把三个长宽高分别是2厘米,宽是3厘米,高是4厘米的小长方体,拼成一个大长方体,这个大长方体的表面积最少是( ),体积是( )。
108cm2
将面积最大的面拼在一起,表面积最少。
72cm3
拼:表面积减小,体积不变
常考题
7.一个正方体木块,把它割成2个长方体后,表面积增加了18平方分米,这个木块原来的表面积是( ),体积是( )。
54cm2
拆:表面积增加,体积不变
27cm3
常考题
8.一个长方体,如果高增加3厘米,就成为一个正方体。这时表面积比原来增加了96平方厘米。原来的长方体的体积是多少立方厘米
96÷4=24(平方厘米)
24÷3=8(厘米)
8×8×(8-3)=320(立方厘米)
答:原来的长方体的体积是320立方厘米。
常考题
9.把一个棱长为6分米的正方体钢锭熔铸成一个长方体钢锭,这个长方体长9分米,宽4分米,求这个长方体钢锭高多少分米。
6×6×6=216(立方分米)
216÷(9×4)=6(分米)
答:这个长方体钢锭高是6分米。
熔铸、锻造:体积不变
常考题
10.如图所示的是5个棱长为20厘米的正方体,露在外面的面的面积是多少
露在外面的面面积:20×20×12=4800(cm2)
答:露在外面的面的面积是4800cm2。
露在外面的面个数:5+4+1+2=12(个)
常考题
4dm2=( )cm2 0.7m3=( )dm3
4035mL=( )L
7.5升=( )dm3=( )cm3
700
4.035
400
11.(1)一块橡皮的体积约是3( )。
(2)一节火车厢的体积约是50( )。
(3)洗衣机的体积约是80( )。
7.5
7500
(4)用钢笔吸墨水,一次大约能吸2( )。
(5)冰箱的容积是180( )。
mL
L
cm3
m3
dm3
转化方法:大换小用乘法,小换大用除法
常考题
12.一个鱼缸从里面量长60厘米、 宽40厘米、高50厘米,将8只螃蟹放入鱼缸内,螃蟹全部潜入水底后水面上升了0.1分米,平均每只螃蟹的体积是多少
0.1分米=1厘米
60×40×1=2400(厘米3)
2400÷8=300(厘米3)
答:平均每只螃蟹的体积是300立方厘米 。
常考题
总复习——图形与几何
第 3 课时
圆
圆的定义
圆是由一条封闭曲线围成的平面图形
1
2
圆的特征
(1)圆有无数条对称轴
(3)同圆或等圆中,直径总是半径的2倍
(4)圆心决定圆的位置,圆的半径(直径)决定圆的大小
知识点
(2)圆有无数条半径和直径
3
圆的周长
圆的周长=圆周率×直径=圆周率×半径×2
用字母表示:C=πd或C=2πr
4
圆的周长与直径的比值叫作圆周率,圆周率是一个无限不循环小数。计算时,π一般取3.14。
圆周率
5
圆的面积
圆的面积=π×半径的平方
用字母表示:S=πr2
圆周长的一半
C半=πd÷2或C半=2πr÷2=πr
6
8
半圆的面积
半圆的面积=π×半径的平方÷2
用字母表示:S半圆=πr2÷2
7
半圆的周长
C半圆=πd÷2+d
或C半圆=2πr÷2+2r=πr+2r=(π+2)r
1.圆内最长的线段是( ),圆规两脚之间的距离是( )。
直径
半径
常考题
2.( )确定圆的位置,( )确定圆的大小。
圆心
半径
3.在同一个圆中,半径的长度是直径( ),直径的长度是半径的( )。
4.圆是( )图形,有( )条对称轴。半圆有( )条对称轴。
2倍
轴对称
无数条
1
5.在边长为6cm的正方形中画一个最大的圆,这个圆的半径是( )。
直径:4×2=8(cm )
一排:32÷8=4(个)
答:这样的圆最多画8个。
几排:16÷8=2(排)
常考题
3cm
6.在一张长32厘米、宽16厘米的长方形纸内画半径4厘米的圆,这样的圆最多能画多少个?(圆不能重叠)
2×4=8(个)
62.8cm
8.汽车车轮的半径是0.3米,它滚动1圈前进多少米?滚动1000圈前进多少米?
7.一种钟表时针长5厘米,走一昼夜走了( )。
周长:3.14×0.3×2=1.884(米)
1.884×1000=1884(米)
常考题
答:它滚动1圈前进1.884米,滚动1000圈前进1884米。
78.5
9.一个钟表的分针长5cm,从1时到2时,分针针尖扫过的面积是( )cm2。
常考题
10.在边长8厘米的正方形纸板上剪下一个最大的圆,这个圆的半径是( )厘米,周长是( )厘米,面积是( )平方厘米。
4
25.12
50.24
11.周长相等的正方形,长方形和圆,( )的面积最大。
圆
12.求下列阴影部分的面积。(单位:厘米)
常考题
4
4×4=16(厘米2)
4÷2=2(厘米)
3.14×22=12.56(厘米2)
16-12.56=3.44(厘米2)
9×2×9=162(厘米2)
3.14×92÷2=127.17(厘米2)
162-127.17=34.83(厘米2)
13.张大叔靠墙用篱笆围了一块半圆形菜地,这个半圆的直径为6米。
(1)篱笆长多少米?
18.84÷2=9.42(米)
3.14×6=18.84(米)
常考题
(2)菜地的面积是多少?
答:篱笆长9.42米。
28.26÷2=14.13(平方米)
答:菜地的面积是14.13平方米。
3.14×(6÷2)2=28.26(平方米)
14.一个直径为8米的圆形花坛,要在花坛外围修一条1米宽的石头小路。
(1)石头小路的面积是多少?
R:8÷2+1=5(米) r:8÷2=4(米)
3.14×(52-42)=28.26(平方米)
常考题
(2)如果每平方米需要花费100元,修这条石头小路总共要花费多少钱?
答:石头小路的面积是28.26平方米。
28.26×100=2826(元)
答:修这条石头小路总共要花费2826元。
总复习——图形与几何
第 4 课时
圆柱圆锥
圆柱的表面积计算公式
知识点
1
圆柱表面积的特殊情况
2
圆柱的体积计算公式
3
圆锥的体积计算公式
4
常考题
1.填一填。
(1)一个底面是正方形的长方体,底面周长是20 cm,高是12 cm,它的表面积是( )cm2,体积是( )cm3。
290
300
(2)(易错题)把两个完全一样的正方体拼成一个长方体后,表面积比原来减少了( )%。(百分号前保留一位小数)
16.7
常考题
2.搬新家啦!梦梦也有了自己的小卧室,她的卧室长4 m、宽2.5 m、高3 m。爸爸准备给她的房间四壁和房顶粉刷天蓝色的环保漆,除去门窗还有9 m2,每平方米环保漆12元,买环保漆一共需要多少元?
4×3×2+2.5×3×2+4×2.5-9=40(m2)
40×12=480(元)
答:买环保漆一共需要480元。
常考题
3.填一填。
(1)一个圆柱的底面半径是2 dm,侧面积是
226.08 dm2,这个圆柱的表面积是( ) dm2,与它等底等高的圆锥的体积是( ) dm3。
(2)一个圆柱和一个圆锥的体积比是4∶3,底面积的比是3∶2,高的比是( )。
251.2
75.36
8∶27
常考题
4.如果把一段圆柱形的木头截成两截,它的表面积会有什么变化呢?变化多少呢?(木头的底面半径是0.3 m,长是2 m)
表面积增加了,
增加的是截面处两个圆面的面积。
答:表面积会增加,增加 0.5652 。
常考题
5.张大伯家有一堆小麦,堆成了圆锥形,张大伯量
得它的底面周长是9.42m,高是2m,这堆小麦的
体积是多少立方米?如果每立方米小麦的质量为
700kg,这堆小麦约重多少千克?
底面积:3.14×(9.42÷3.14÷2)2=7.065(m2)
体积:
质量:
4.71×700=3297(kg)
答:这堆小麦的体积是4.71立方米,约重3297千克。
常考题
6.下图中的蒙古包是由一个圆柱和一个圆锥组成的(单位:m)。这个蒙古包占地多少?内部的空间约是多少(得数保留整数)
常考题
7.一个底面半径是6 cm的圆柱形玻璃容器里装有一部分水,水中浸没着一个高9 cm的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.5 cm。这个圆锥形铅锤的底面积是多少平方厘米?
3×3.14×62×0.5÷9=18.84(cm2)
答:这个圆锥形铅锤的底面积是18.84 cm2。
常考题
8.在一个棱长为4 cm的正方体的顶部挖去一个底面半径为1 cm、高为2 cm的圆柱,求剩下图形的表面积和体积。
表面积:4×4×6+3.14×1×2×2=108.56(cm2)
体积:4×4×4-3.14×12×2=57.72(cm3)
图
形
与
几
何
多边形的面积
长方体和正方体
圆
圆柱圆锥
总复习
1
2
3
4
总复习——图形与几何
第 1 课时
多边形的面积
平行四边形
平行四边形的面积=底×高
字母表示:S=ah
平行四边形的底=平行四边形的面积÷平行四边形的高
字母表示:a=S÷h
1
平行四边形的高=平行四边形的面积÷平行四边形的底
字母表示:h=S÷a
知识点
三角形
三角形的面积=底×高÷2
字母表示:S=ah÷2
三角形的底=三角形的面积×2÷三角形的高
字母表示:a =2S÷h
2
三角形的高=三角形的面积×2÷三角形的底
字母表示:h =2S÷a
知识点
梯形
梯形的面积=(上底+下底)×高÷2
字母表示:S=(a+b)×h÷2
梯形的上底=梯形的面积×2÷梯形的高-下底
字母表示:a=2S÷h-b
3
梯形的下底=梯形的面积×2÷梯形的高-上底
字母表示:b=2S÷h-a
知识点
梯形的高=梯形的面积×2÷梯形的上底+下底之和
字母表示:h =2S÷(a+b)
1.一块平行四边形钢板的面积是1391平方米,底是21.4米,它的高是多少米
1391÷21.4=65(米)
答:它的高是65米。
常考题
2.一块平行四边形街头广告牌,底是8.5m,高是5.4m。要粉刷这块广告牌,每平方米要用油漆0.5kg,至少需要准备多少千克油漆?
8.5×5.4×0.5=22.95(kg)
答:至少需要准备22.95千克油漆。
常考题
3.如图,一块平行四边形的草地中间有一条长8m、宽1m的小路,求草地的面积。
(25-1)×8=192(m2)
答:草地的面积是192m2。
常考题
4.填空。
(1)一个平行四边形的面积是48平方米,与它等底等高的三角形的面积是( )平方米。
(2)一个三角形和一个平行四边形等底等高,平行四边形的面积与三角形的面积和是27平方厘米,这个三角形的面积是( )平方厘米。
常考题
24
9
5.一个三角形的面积是12.6平方米,底是3米, 这个三角形的高是多少米
12.6×2÷3=8.4(米)
答:这个三角形的高是8.4米。
常考题
6.已知一个三角形的鱼池底是50米,高是40米,它的面积是多少平方米 如果每平方米可养鱼20条,那么这个鱼池总共可养鱼多少条?
50×40÷2×20=20000(条)
答:这个鱼池共可以养20000条鱼。
常考题
7.判断。(对的打“√”,错的打“ ”)
(1)梯形的面积等于平行四边形面积的一半。
( )
常考题
(2)两个完全一样的直角梯形,可以拼成一个 长方形。 ( )
(3)一个上底是5厘米、下底是8厘米、高是3厘米的梯形,它的面积是12平方厘米。( )
√
8.一块梯形花园,上底是35米,下底是25米,面积是1140平方米,高是多少米
1140×2÷(35+25)=38(米)
答:高是38米。
常考题
总复习——图形与几何
第 2 课时
长方体和正方体
长方体和正方体的特点
顶点 个数
面 个数
形状
大小关系
棱 条数
长度关系
8个
8个
6个
6个
正方形
长方形或正方形
大小相同
相对的两个面大小相同
12条
12条
长度相等
相对的棱长度相等
知识点
1
长方体和正方体的棱长总和
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
2
3
长方体的表面积=(长×宽+长×高+宽×高)×2
长方体和正方体的表面积
正方体的表面积=棱长×棱长×6
4
长方体和正方体的体积
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
5
体积与容积的区别
体积是指物体所占空间的大小。
容积是指容器所容纳物体的体积。
6
体积单位:立方米(m3)、立方分米(dm3)、
立方厘米(cm3)
常用的体积单位与容积单位
容积单位:升(L)、毫升(mL)
单位转化方法:大换小用乘法,小换大用除法
7
不规则物体的体积
不规则物体的体积=底面积×水面上升的高度
1.右图是一个长方体盒子相交于同一个顶点的三条棱,它的棱长总和是( )厘米,表面积是( )平方厘米,体积( )立方厘米。
60
148
120
4cm
6cm
5cm
常考题
2.把一根96厘米长的铁丝做成一个长方体框架,长10厘米,宽8厘米,高是( )厘米。
6
3.做两个无盖的长方体水箱,水箱的底面是边长为
3.5dm的正方形,高为4dm,做这两个水箱至少要
用多少平方分米的铁皮?
(3.5×4×4+3.5×3.5)×2
=68.25×2
答:做这对水箱至少要用136.5平方分米的铁皮。
=136.5(平方分米)
常考题
3
正方体棱长扩大几倍,棱长总和就扩大几倍,表面积扩大平方倍,体积扩大立方倍。
4.一个长方体的长、宽、高各扩大到原来3倍,它的棱长总和扩大到原来的( )倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
9
27
长方体长、宽、高扩大几倍,棱长总和就扩大几倍,表面积扩大平方倍,体积扩大立方倍。
常考题
A
5.把一个长方体分成几个小长方体后,小长方体
的体积和原长方体的体积相比较,( )。
A.不变 B.比原来小了
C.比原来大了 D.无法确定
常考题
6.把三个长宽高分别是2厘米,宽是3厘米,高是4厘米的小长方体,拼成一个大长方体,这个大长方体的表面积最少是( ),体积是( )。
108cm2
将面积最大的面拼在一起,表面积最少。
72cm3
拼:表面积减小,体积不变
常考题
7.一个正方体木块,把它割成2个长方体后,表面积增加了18平方分米,这个木块原来的表面积是( ),体积是( )。
54cm2
拆:表面积增加,体积不变
27cm3
常考题
8.一个长方体,如果高增加3厘米,就成为一个正方体。这时表面积比原来增加了96平方厘米。原来的长方体的体积是多少立方厘米
96÷4=24(平方厘米)
24÷3=8(厘米)
8×8×(8-3)=320(立方厘米)
答:原来的长方体的体积是320立方厘米。
常考题
9.把一个棱长为6分米的正方体钢锭熔铸成一个长方体钢锭,这个长方体长9分米,宽4分米,求这个长方体钢锭高多少分米。
6×6×6=216(立方分米)
216÷(9×4)=6(分米)
答:这个长方体钢锭高是6分米。
熔铸、锻造:体积不变
常考题
10.如图所示的是5个棱长为20厘米的正方体,露在外面的面的面积是多少
露在外面的面面积:20×20×12=4800(cm2)
答:露在外面的面的面积是4800cm2。
露在外面的面个数:5+4+1+2=12(个)
常考题
4dm2=( )cm2 0.7m3=( )dm3
4035mL=( )L
7.5升=( )dm3=( )cm3
700
4.035
400
11.(1)一块橡皮的体积约是3( )。
(2)一节火车厢的体积约是50( )。
(3)洗衣机的体积约是80( )。
7.5
7500
(4)用钢笔吸墨水,一次大约能吸2( )。
(5)冰箱的容积是180( )。
mL
L
cm3
m3
dm3
转化方法:大换小用乘法,小换大用除法
常考题
12.一个鱼缸从里面量长60厘米、 宽40厘米、高50厘米,将8只螃蟹放入鱼缸内,螃蟹全部潜入水底后水面上升了0.1分米,平均每只螃蟹的体积是多少
0.1分米=1厘米
60×40×1=2400(厘米3)
2400÷8=300(厘米3)
答:平均每只螃蟹的体积是300立方厘米 。
常考题
总复习——图形与几何
第 3 课时
圆
圆的定义
圆是由一条封闭曲线围成的平面图形
1
2
圆的特征
(1)圆有无数条对称轴
(3)同圆或等圆中,直径总是半径的2倍
(4)圆心决定圆的位置,圆的半径(直径)决定圆的大小
知识点
(2)圆有无数条半径和直径
3
圆的周长
圆的周长=圆周率×直径=圆周率×半径×2
用字母表示:C=πd或C=2πr
4
圆的周长与直径的比值叫作圆周率,圆周率是一个无限不循环小数。计算时,π一般取3.14。
圆周率
5
圆的面积
圆的面积=π×半径的平方
用字母表示:S=πr2
圆周长的一半
C半=πd÷2或C半=2πr÷2=πr
6
8
半圆的面积
半圆的面积=π×半径的平方÷2
用字母表示:S半圆=πr2÷2
7
半圆的周长
C半圆=πd÷2+d
或C半圆=2πr÷2+2r=πr+2r=(π+2)r
1.圆内最长的线段是( ),圆规两脚之间的距离是( )。
直径
半径
常考题
2.( )确定圆的位置,( )确定圆的大小。
圆心
半径
3.在同一个圆中,半径的长度是直径( ),直径的长度是半径的( )。
4.圆是( )图形,有( )条对称轴。半圆有( )条对称轴。
2倍
轴对称
无数条
1
5.在边长为6cm的正方形中画一个最大的圆,这个圆的半径是( )。
直径:4×2=8(cm )
一排:32÷8=4(个)
答:这样的圆最多画8个。
几排:16÷8=2(排)
常考题
3cm
6.在一张长32厘米、宽16厘米的长方形纸内画半径4厘米的圆,这样的圆最多能画多少个?(圆不能重叠)
2×4=8(个)
62.8cm
8.汽车车轮的半径是0.3米,它滚动1圈前进多少米?滚动1000圈前进多少米?
7.一种钟表时针长5厘米,走一昼夜走了( )。
周长:3.14×0.3×2=1.884(米)
1.884×1000=1884(米)
常考题
答:它滚动1圈前进1.884米,滚动1000圈前进1884米。
78.5
9.一个钟表的分针长5cm,从1时到2时,分针针尖扫过的面积是( )cm2。
常考题
10.在边长8厘米的正方形纸板上剪下一个最大的圆,这个圆的半径是( )厘米,周长是( )厘米,面积是( )平方厘米。
4
25.12
50.24
11.周长相等的正方形,长方形和圆,( )的面积最大。
圆
12.求下列阴影部分的面积。(单位:厘米)
常考题
4
4×4=16(厘米2)
4÷2=2(厘米)
3.14×22=12.56(厘米2)
16-12.56=3.44(厘米2)
9×2×9=162(厘米2)
3.14×92÷2=127.17(厘米2)
162-127.17=34.83(厘米2)
13.张大叔靠墙用篱笆围了一块半圆形菜地,这个半圆的直径为6米。
(1)篱笆长多少米?
18.84÷2=9.42(米)
3.14×6=18.84(米)
常考题
(2)菜地的面积是多少?
答:篱笆长9.42米。
28.26÷2=14.13(平方米)
答:菜地的面积是14.13平方米。
3.14×(6÷2)2=28.26(平方米)
14.一个直径为8米的圆形花坛,要在花坛外围修一条1米宽的石头小路。
(1)石头小路的面积是多少?
R:8÷2+1=5(米) r:8÷2=4(米)
3.14×(52-42)=28.26(平方米)
常考题
(2)如果每平方米需要花费100元,修这条石头小路总共要花费多少钱?
答:石头小路的面积是28.26平方米。
28.26×100=2826(元)
答:修这条石头小路总共要花费2826元。
总复习——图形与几何
第 4 课时
圆柱圆锥
圆柱的表面积计算公式
知识点
1
圆柱表面积的特殊情况
2
圆柱的体积计算公式
3
圆锥的体积计算公式
4
常考题
1.填一填。
(1)一个底面是正方形的长方体,底面周长是20 cm,高是12 cm,它的表面积是( )cm2,体积是( )cm3。
290
300
(2)(易错题)把两个完全一样的正方体拼成一个长方体后,表面积比原来减少了( )%。(百分号前保留一位小数)
16.7
常考题
2.搬新家啦!梦梦也有了自己的小卧室,她的卧室长4 m、宽2.5 m、高3 m。爸爸准备给她的房间四壁和房顶粉刷天蓝色的环保漆,除去门窗还有9 m2,每平方米环保漆12元,买环保漆一共需要多少元?
4×3×2+2.5×3×2+4×2.5-9=40(m2)
40×12=480(元)
答:买环保漆一共需要480元。
常考题
3.填一填。
(1)一个圆柱的底面半径是2 dm,侧面积是
226.08 dm2,这个圆柱的表面积是( ) dm2,与它等底等高的圆锥的体积是( ) dm3。
(2)一个圆柱和一个圆锥的体积比是4∶3,底面积的比是3∶2,高的比是( )。
251.2
75.36
8∶27
常考题
4.如果把一段圆柱形的木头截成两截,它的表面积会有什么变化呢?变化多少呢?(木头的底面半径是0.3 m,长是2 m)
表面积增加了,
增加的是截面处两个圆面的面积。
答:表面积会增加,增加 0.5652 。
常考题
5.张大伯家有一堆小麦,堆成了圆锥形,张大伯量
得它的底面周长是9.42m,高是2m,这堆小麦的
体积是多少立方米?如果每立方米小麦的质量为
700kg,这堆小麦约重多少千克?
底面积:3.14×(9.42÷3.14÷2)2=7.065(m2)
体积:
质量:
4.71×700=3297(kg)
答:这堆小麦的体积是4.71立方米,约重3297千克。
常考题
6.下图中的蒙古包是由一个圆柱和一个圆锥组成的(单位:m)。这个蒙古包占地多少?内部的空间约是多少(得数保留整数)
常考题
7.一个底面半径是6 cm的圆柱形玻璃容器里装有一部分水,水中浸没着一个高9 cm的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.5 cm。这个圆锥形铅锤的底面积是多少平方厘米?
3×3.14×62×0.5÷9=18.84(cm2)
答:这个圆锥形铅锤的底面积是18.84 cm2。
常考题
8.在一个棱长为4 cm的正方体的顶部挖去一个底面半径为1 cm、高为2 cm的圆柱,求剩下图形的表面积和体积。
表面积:4×4×6+3.14×1×2×2=108.56(cm2)
体积:4×4×4-3.14×12×2=57.72(cm3)
