沪教版九年级数学上册 25.2求锐角的三角比的值(含解析)
文档属性
| 名称 | 沪教版九年级数学上册 25.2求锐角的三角比的值(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 11:03:39 | ||
图片预览



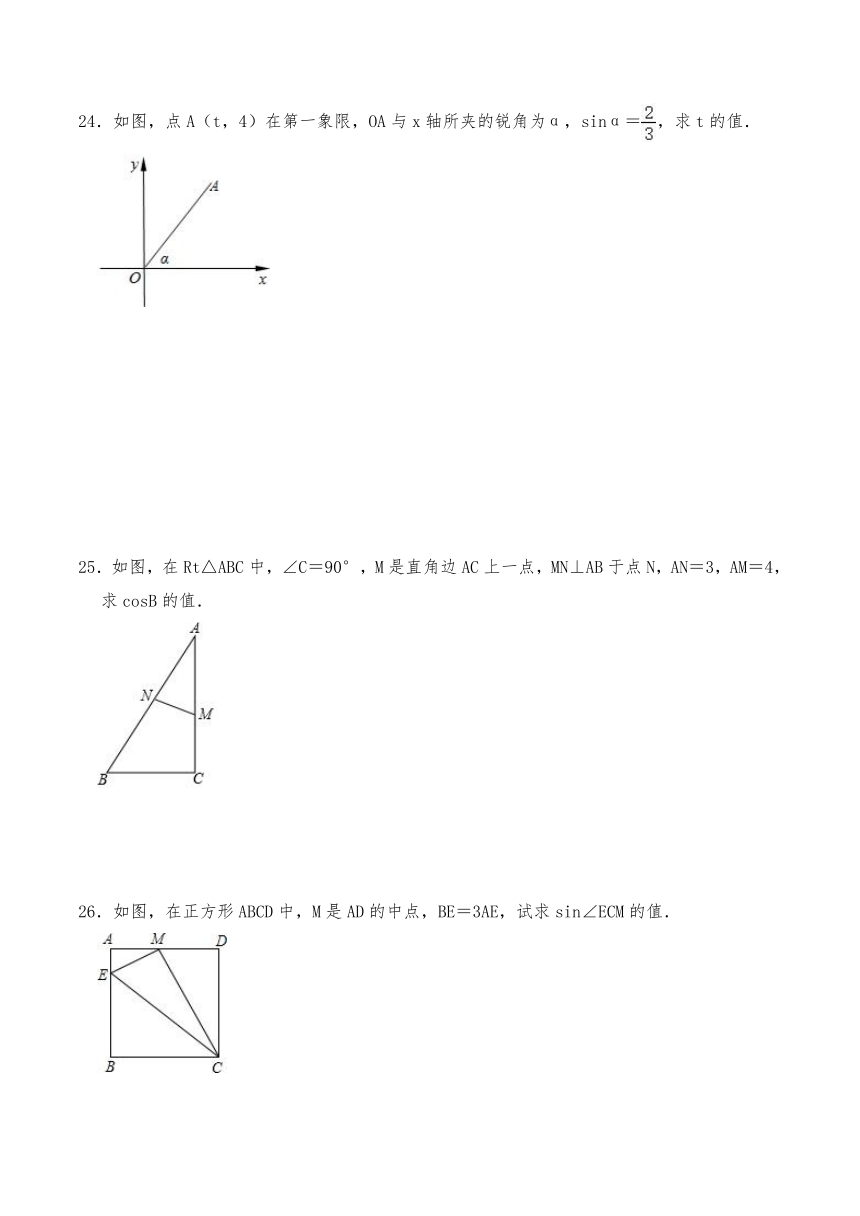

文档简介
25.2求锐角的三角比的值
一.选择题
1.Rt△ABC的边长都扩大2倍,则cosA的值( )
A.不变 B.变大 C.变小 D.无法判断
2.在Rt△ABC中,∠C=90°,AB=4,AC=3,那么cosA的值是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,AC=1,BC=3,那么∠A的正弦值是( )
A. B. C.3 D.
4.计算的值是( )
A. B.1 C. D.3
5.在△ABC中,∠C=90°,AB=5,BC=4,则sinA的值是( )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,,则cosA的值为( )
A. B. C. D.
7.△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形
B.钝角三角形
C.锐角三角形
D.锐角三角形或钝角三角形
8.已知α为锐角,,则α等于( )
A.30° B.50° C.60° D.80°
9.若sinα>cosα,则锐角α的取值范围是( )
A.0°<α<45° B.30°<α<45° C.45°<α<60° D.45°<α<90°
10.下列选项正确的是( )
A.sin31°+cos31°<1 B.sin31°+cos31°>2
C.sin31°+cos31°=1 D.sin31°+cos31°>1
二.填空题
11.已知在△ABC中,∠C=90°,AB=8,AC=6,那么cosA的值是 .
12.若2cos∠A=1,则锐角∠A= °
13.已知sinα sin45°=,则锐角α为 .
14.在△ABC中,若,则∠C= .
15.比较大小:sin80° sin50°(填“>”或“<”).
16.如果在平面直角坐标系xOy中,点P的坐标为(3,4),射线OP与x轴的正半轴所夹的角为α,那么α的余弦值等于 .
17.在Rt△ABC中,∠C=90°,AC=1,BC=2,则cos(∠A﹣∠B)= .
18.因为,,所以cos240°=cos(180°+60°)=﹣cos60°,由此猜想:当α为锐角时,有cos(180°+α)=﹣cosα,由此可知:cos210°= .
三.解答题
19.计算:2sin30°+cos60°﹣cos245°
20.根据图示填空:
(1)sinB==
(2)cos∠ACD=.
21.在△ABC中,∠C=90°,AC=4,BC=2,求∠B的余弦值.
22.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,求sinA cosA的值.
23.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.若a=2,sin,求b和c.
24.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=,求t的值.
25.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
26.如图,在正方形ABCD中,M是AD的中点,BE=3AE,试求sin∠ECM的值.
答案
一.选择题
1.
【分析】根据题意可得所得的三角形与原三角形相似,从而可得∠A的大小没有发生变化,即可解答.
【解析】解:∵Rt△ABC的边长都扩大2倍,
∴所得的三角形与原三角形相似,
∴∠A的大小没有发生变化,
∴cosA的值不变,
故选:A.
2.
【分析】利用锐角三角函数的定义,进行计算即可解答.
【解析】解:在Rt△ABC中,∠C=90°,AB=4,AC=3,
∴cosA==,
故选:C.
3.
【分析】先在Rt△ABC中,利用勾股定理求出AB的长,然后再利用锐角三角函数的定义进行计算即可解答.
【解析】解:在Rt△ABC中,∠C=90°,AC=1,BC=3,
∴AB===,
∴sinA===,
故选:A.
4.
【分析】先计算,再计算二次根式乘法即可.
【解析】解;,
故选:C.
5.
【分析】根据锐角三角函数的正弦值的定义解答即可.
【解析】解:在△ABC中,∠C=90°,AB=5,BC=4,
则sinA==,
故选:A.
6.
【分析】令BC=x,则AB=3x,由勾股定理求出AC==2x,由锐角的余弦定义即可求出cosA==.
【解析】解:Rt△ABC中,∠C=90°,sinA==,
∴令BC=x,则AB=3x,
∴AC==2x,
∴cosA==.
故选:B.
7.
【分析】直接利用特殊角的三角函数值得出∠A,∠B的度数,进而得出答案.
【解析】解:∵sinA=,cosB=,
∴∠A=45°,∠B=60°,
∴∠C=75°,
∴△ABC的形状是锐角三角形.
故选:C.
8.
【分析】直接利用特殊角的三角函数值求得α﹣20°的值,然后求得α的度数即可.
【解析】解:∵已知α为锐角,cos(α﹣20°)=,
∴α﹣20°=30°,
∴α=50°.
故选:B.
9.
【分析】利用cosα=sin(90°﹣α),载根据锐角三角函数的增减性,即可求出α的取值范围.
【解析】解:∵cosα=sin(90°﹣α),sinα>cosα,
∴sinα>sin(90°﹣α),
∴α>90°﹣α,
∴α>45°,
又∵α为锐角,
∴45°<x<90°,
故选:D.
10.
【分析】根据锐角三角函数的定义进行计算即可判断.
【解析】解:如图:
在Rt△ABC中,∠C=90°,∠A=31°,
∴sin31°=,cos31°=,
∴sin31°+cos31°=+=,
∵BC+AC>AB,
∴+>1,
∴sin31°+cos31°>1,
故选:D.
二.填空题
11.
【分析】根据余弦的定义即可求解.
【解析】解:在△ABC中,∠C=90°,AB=8,AC=6,
∴cosA===.
故答案为:.
12.
【分析】先计算出cos∠A=,然后根据60°的余弦值为求解.
【解析】解:∵2cos∠A=1,
∴cos∠A=,
∴锐角∠A=60°.
故答案为:60.
13.
【分析】直接利用特殊角的三角函数值代入得出sinα=,即可得出答案.
【解析】解:∵sinα sin45°=,
∴sinα =,
故sinα=,
则锐角α为45°.
故答案为:45°.
14.
【分析】利用非负数和为零得出2sinA﹣1=0,,求出∠A、∠B度数,再由三角形内角和定理求解即可.
【解析】解:∵,
∴2sinA﹣1=0,,
∴,,
∴∠A=30°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=105°.
故答案为:105°.
15.
【分析】根据一个锐角的正弦值随着角度的增大而增大进行判断即可.
【解析】解:由于“一个锐角的正弦值随着角度的增大而增大”可知,
∵80°>50°,
∴sin80°>sin50°,
故答案为:>.
16.
【分析】画出图形,根据勾股定理求出OP,根据锐角三角函数的定义求出即可.
【解析】
解:过P作PA⊥x轴于A,
∵P(3,4),
∴PA=4,OA=3,
由勾股定理得:OP=5,
∴α的余弦值是=,
过答案为:.
17.
【分析】设CD=x,根据勾股定理列方程,求出x的值,再得出AD=BD=2﹣x,再根据锐角三角函数的定义求出cos(∠A﹣∠B)即可.
【解析】解:过A作∠BAD=∠B,交BC于点D,
设CD=x,
∵BC=2,
∴BD=AD=2﹣x,
根据勾股定理,AC2+CD2=AD2,即12+x2=(2﹣x)2,
解得x=,
∴AD=2﹣=,
cos(∠A﹣∠B)=cos∠CAD===,
故答案为:.
18.
【分析】当α为锐角时有cos(180°+α)=﹣cosα.把210°代入计算即可.
【解析】解:∵cos(180°+α)=﹣cosα,
∴.
故答案为:.
三.解答题
19.解:2sin30°+cos60°﹣cos245°===1
20.解:(1)sinB==.
故答案为:BC,AC;
(2)cos∠ACD=.
故答案为:AC.
21.解:如图,
在Rt△ABC中,∵BC=2、AC=4,
∴AB===2,
则cosB===.
22.解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得,BC===4,
所以sinA==,cosA==,
所以sinA cosA=×=.
答:sinA cosA的值为.
23.解:如图,
∵a=2,sin,
∴c===6,
则b===4.
24.解:过A作AB⊥x轴于B.
∴,
∵,
∴,
∵A(t,4),
∴AB=4,
∴OA=6,
∴.
25.解:∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==x,
在Rt△ABC中,cosB===.
26.解:设AE=x,则BE=3x,BC=4x,AM=2x,CD=4x,
∴EC==5x,
EM==x,
CM==2x,
∴EM2+CM2=CE2,
∴△CEM是直角三角形,
∴sin∠ECM==.
一.选择题
1.Rt△ABC的边长都扩大2倍,则cosA的值( )
A.不变 B.变大 C.变小 D.无法判断
2.在Rt△ABC中,∠C=90°,AB=4,AC=3,那么cosA的值是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,AC=1,BC=3,那么∠A的正弦值是( )
A. B. C.3 D.
4.计算的值是( )
A. B.1 C. D.3
5.在△ABC中,∠C=90°,AB=5,BC=4,则sinA的值是( )
A. B. C. D.
6.在Rt△ABC中,∠C=90°,,则cosA的值为( )
A. B. C. D.
7.△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC的形状是( )
A.直角三角形
B.钝角三角形
C.锐角三角形
D.锐角三角形或钝角三角形
8.已知α为锐角,,则α等于( )
A.30° B.50° C.60° D.80°
9.若sinα>cosα,则锐角α的取值范围是( )
A.0°<α<45° B.30°<α<45° C.45°<α<60° D.45°<α<90°
10.下列选项正确的是( )
A.sin31°+cos31°<1 B.sin31°+cos31°>2
C.sin31°+cos31°=1 D.sin31°+cos31°>1
二.填空题
11.已知在△ABC中,∠C=90°,AB=8,AC=6,那么cosA的值是 .
12.若2cos∠A=1,则锐角∠A= °
13.已知sinα sin45°=,则锐角α为 .
14.在△ABC中,若,则∠C= .
15.比较大小:sin80° sin50°(填“>”或“<”).
16.如果在平面直角坐标系xOy中,点P的坐标为(3,4),射线OP与x轴的正半轴所夹的角为α,那么α的余弦值等于 .
17.在Rt△ABC中,∠C=90°,AC=1,BC=2,则cos(∠A﹣∠B)= .
18.因为,,所以cos240°=cos(180°+60°)=﹣cos60°,由此猜想:当α为锐角时,有cos(180°+α)=﹣cosα,由此可知:cos210°= .
三.解答题
19.计算:2sin30°+cos60°﹣cos245°
20.根据图示填空:
(1)sinB==
(2)cos∠ACD=.
21.在△ABC中,∠C=90°,AC=4,BC=2,求∠B的余弦值.
22.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,求sinA cosA的值.
23.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.若a=2,sin,求b和c.
24.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=,求t的值.
25.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
26.如图,在正方形ABCD中,M是AD的中点,BE=3AE,试求sin∠ECM的值.
答案
一.选择题
1.
【分析】根据题意可得所得的三角形与原三角形相似,从而可得∠A的大小没有发生变化,即可解答.
【解析】解:∵Rt△ABC的边长都扩大2倍,
∴所得的三角形与原三角形相似,
∴∠A的大小没有发生变化,
∴cosA的值不变,
故选:A.
2.
【分析】利用锐角三角函数的定义,进行计算即可解答.
【解析】解:在Rt△ABC中,∠C=90°,AB=4,AC=3,
∴cosA==,
故选:C.
3.
【分析】先在Rt△ABC中,利用勾股定理求出AB的长,然后再利用锐角三角函数的定义进行计算即可解答.
【解析】解:在Rt△ABC中,∠C=90°,AC=1,BC=3,
∴AB===,
∴sinA===,
故选:A.
4.
【分析】先计算,再计算二次根式乘法即可.
【解析】解;,
故选:C.
5.
【分析】根据锐角三角函数的正弦值的定义解答即可.
【解析】解:在△ABC中,∠C=90°,AB=5,BC=4,
则sinA==,
故选:A.
6.
【分析】令BC=x,则AB=3x,由勾股定理求出AC==2x,由锐角的余弦定义即可求出cosA==.
【解析】解:Rt△ABC中,∠C=90°,sinA==,
∴令BC=x,则AB=3x,
∴AC==2x,
∴cosA==.
故选:B.
7.
【分析】直接利用特殊角的三角函数值得出∠A,∠B的度数,进而得出答案.
【解析】解:∵sinA=,cosB=,
∴∠A=45°,∠B=60°,
∴∠C=75°,
∴△ABC的形状是锐角三角形.
故选:C.
8.
【分析】直接利用特殊角的三角函数值求得α﹣20°的值,然后求得α的度数即可.
【解析】解:∵已知α为锐角,cos(α﹣20°)=,
∴α﹣20°=30°,
∴α=50°.
故选:B.
9.
【分析】利用cosα=sin(90°﹣α),载根据锐角三角函数的增减性,即可求出α的取值范围.
【解析】解:∵cosα=sin(90°﹣α),sinα>cosα,
∴sinα>sin(90°﹣α),
∴α>90°﹣α,
∴α>45°,
又∵α为锐角,
∴45°<x<90°,
故选:D.
10.
【分析】根据锐角三角函数的定义进行计算即可判断.
【解析】解:如图:
在Rt△ABC中,∠C=90°,∠A=31°,
∴sin31°=,cos31°=,
∴sin31°+cos31°=+=,
∵BC+AC>AB,
∴+>1,
∴sin31°+cos31°>1,
故选:D.
二.填空题
11.
【分析】根据余弦的定义即可求解.
【解析】解:在△ABC中,∠C=90°,AB=8,AC=6,
∴cosA===.
故答案为:.
12.
【分析】先计算出cos∠A=,然后根据60°的余弦值为求解.
【解析】解:∵2cos∠A=1,
∴cos∠A=,
∴锐角∠A=60°.
故答案为:60.
13.
【分析】直接利用特殊角的三角函数值代入得出sinα=,即可得出答案.
【解析】解:∵sinα sin45°=,
∴sinα =,
故sinα=,
则锐角α为45°.
故答案为:45°.
14.
【分析】利用非负数和为零得出2sinA﹣1=0,,求出∠A、∠B度数,再由三角形内角和定理求解即可.
【解析】解:∵,
∴2sinA﹣1=0,,
∴,,
∴∠A=30°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=105°.
故答案为:105°.
15.
【分析】根据一个锐角的正弦值随着角度的增大而增大进行判断即可.
【解析】解:由于“一个锐角的正弦值随着角度的增大而增大”可知,
∵80°>50°,
∴sin80°>sin50°,
故答案为:>.
16.
【分析】画出图形,根据勾股定理求出OP,根据锐角三角函数的定义求出即可.
【解析】
解:过P作PA⊥x轴于A,
∵P(3,4),
∴PA=4,OA=3,
由勾股定理得:OP=5,
∴α的余弦值是=,
过答案为:.
17.
【分析】设CD=x,根据勾股定理列方程,求出x的值,再得出AD=BD=2﹣x,再根据锐角三角函数的定义求出cos(∠A﹣∠B)即可.
【解析】解:过A作∠BAD=∠B,交BC于点D,
设CD=x,
∵BC=2,
∴BD=AD=2﹣x,
根据勾股定理,AC2+CD2=AD2,即12+x2=(2﹣x)2,
解得x=,
∴AD=2﹣=,
cos(∠A﹣∠B)=cos∠CAD===,
故答案为:.
18.
【分析】当α为锐角时有cos(180°+α)=﹣cosα.把210°代入计算即可.
【解析】解:∵cos(180°+α)=﹣cosα,
∴.
故答案为:.
三.解答题
19.解:2sin30°+cos60°﹣cos245°===1
20.解:(1)sinB==.
故答案为:BC,AC;
(2)cos∠ACD=.
故答案为:AC.
21.解:如图,
在Rt△ABC中,∵BC=2、AC=4,
∴AB===2,
则cosB===.
22.解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得,BC===4,
所以sinA==,cosA==,
所以sinA cosA=×=.
答:sinA cosA的值为.
23.解:如图,
∵a=2,sin,
∴c===6,
则b===4.
24.解:过A作AB⊥x轴于B.
∴,
∵,
∴,
∵A(t,4),
∴AB=4,
∴OA=6,
∴.
25.解:∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==x,
在Rt△ABC中,cosB===.
26.解:设AE=x,则BE=3x,BC=4x,AM=2x,CD=4x,
∴EC==5x,
EM==x,
CM==2x,
∴EM2+CM2=CE2,
∴△CEM是直角三角形,
∴sin∠ECM==.
