沪教版九年级数学上册 25.4 解直角三角形的应用(含解析)
文档属性
| 名称 | 沪教版九年级数学上册 25.4 解直角三角形的应用(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 11:06:35 | ||
图片预览


文档简介
25.4 解直角三角形的应用
一、单选题
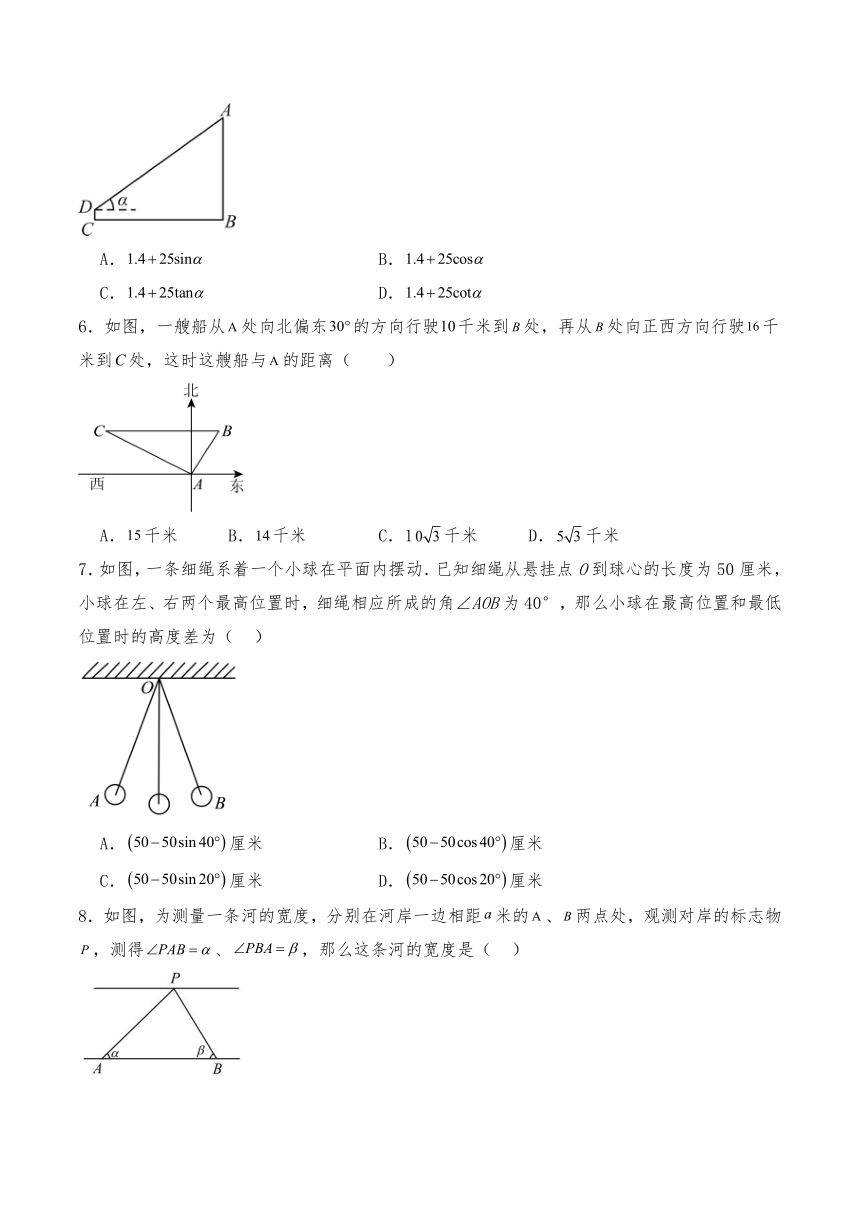
1.如果斜坡的坡度为,那么这条斜坡的坡角为( )
A.75度 B.60度 C.45度 D.30度
2.进博会期间,从一架离地米的无人机上,测得地面监测点的俯角是,那么此时无人机与地面监测点的距离是( )
A.米 B.米 C.米 D.米
3.许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图,的长为50米,与的夹角为,则高是()
A.米 B.米 C.米 D.米
4.如图,已知直线为水平线,,从甲楼的楼顶处观测乙楼的楼顶处的俯角是( )
A. B. C. D.
5.如图,为了测量学校教学楼的高度,在操场的处架起测角仪,测角仪的高米,从点测得教学大楼顶端的仰角为,测角仪底部到大楼底部的距离是米,那么教学大楼的高是( )
A. B.
C. D.
6.如图,一艘船从处向北偏东的方向行驶千米到处,再从处向正西方向行驶千米到处,这时这艘船与的距离( )
A.千米 B.千米 C.1千米 D.千米
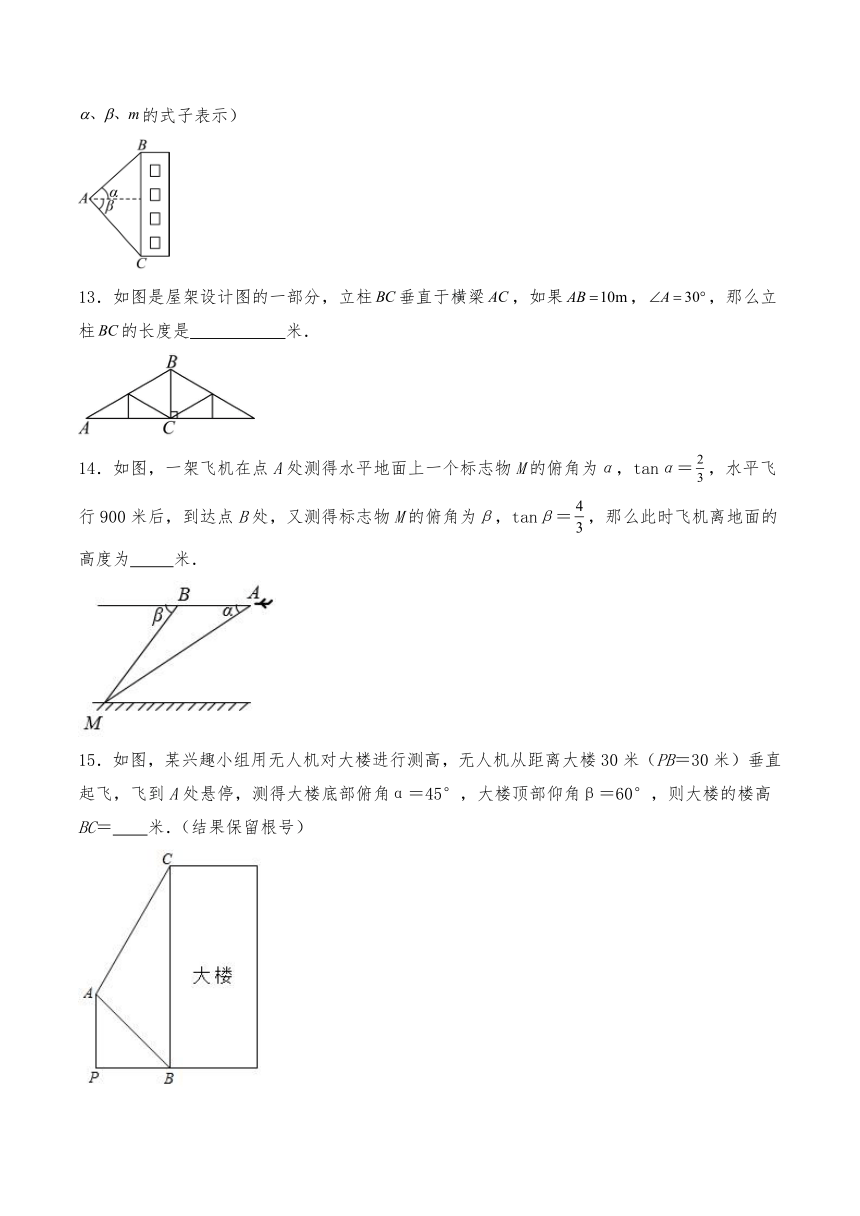
7.如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在左、右两个最高位置时,细绳相应所成的角∠AOB为40°,那么小球在最高位置和最低位置时的高度差为( )
A.厘米 B.厘米
C.厘米 D.厘米
8.如图,为测量一条河的宽度,分别在河岸一边相距米的、两点处,观测对岸的标志物,测得、,那么这条河的宽度是( )
A.米 B.米
C.米 D.米
9.共享单车为市民出行提供了便利.图1为单车实物图,图2为单车示意图,与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线方向调节.已知,,,车轮半径为,,小明体验后觉得当坐垫C离地面高度为时骑着比较舒适,此时的长约为( )(结果精确到,参考数据:,,)
A. B. C. D.
10.某同学利用数学知识测量建筑物的高度,他从点出发沿着坡度为的斜坡步行米到达点处,用测角仪测得建筑物顶端的仰角为,建筑物底端的俯角为.若为水平的地面,点在同一平面内,建筑物和测角仪与水平方向垂直,若米,则此建筑物的高度约为( )(精确到米,参考数据:,,)
A.米 B.米 C.米 D.米
二、填空题
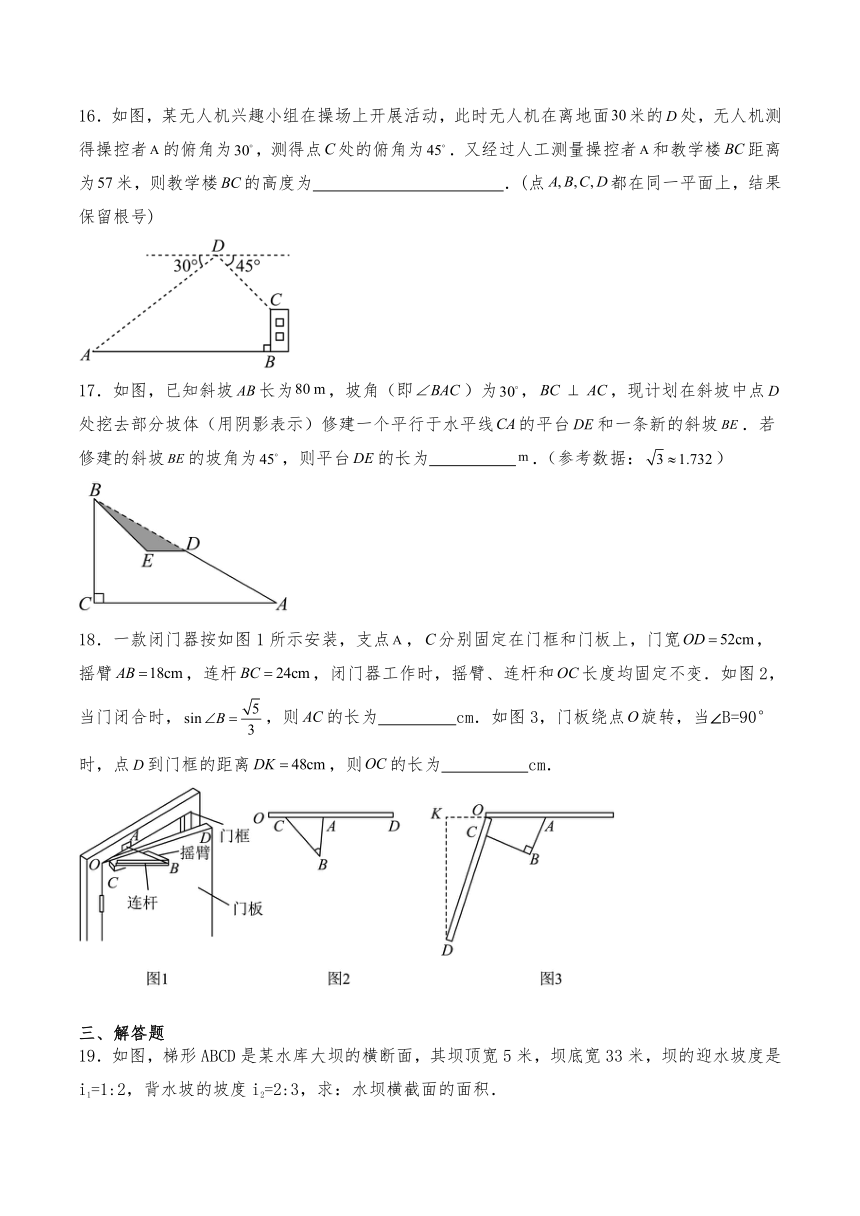
11.已知斜坡坡度为,如果斜坡长为米,那么斜坡的高为 米.
12.如图,热气球的探测器显示,从热气球A处看一栋楼顶部B的仰角为,看这栋楼底部C的俯角为,热气球A处与楼的水平距离为m米,那么这栋楼的高度为 米.(用含的式子表示)
13.如图是屋架设计图的一部分,立柱垂直于横梁,如果,,那么立柱的长度是 米.
14.如图,一架飞机在点A处测得水平地面上一个标志物M的俯角为α,tanα=,水平飞行900米后,到达点B处,又测得标志物M的俯角为β,tanβ=,那么此时飞机离地面的高度为 米.
15.如图,某兴趣小组用无人机对大楼进行测高,无人机从距离大楼30米(PB=30米)垂直起飞,飞到A处悬停,测得大楼底部俯角α=45°,大楼顶部仰角β=60°,则大楼的楼高BC= 米.(结果保留根号)
16.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的处,无人机测得操控者的俯角为,测得点处的俯角为.又经过人工测量操控者和教学楼距离为米,则教学楼的高度为 .(点都在同一平面上,结果保留根号)
17.如图,已知斜坡长为,坡角(即)为,,现计划在斜坡中点处挖去部分坡体(用阴影表示)修建一个平行于水平线的平台和一条新的斜坡.若修建的斜坡的坡角为,则平台的长为 .(参考数据:)
18.一款闭门器按如图1所示安装,支点,分别固定在门框和门板上,门宽,摇臂,连杆,闭门器工作时,摇臂、连杆和长度均固定不变.如图2,当门闭合时,,则的长为 cm.如图3,门板绕点旋转,当∠B=90°时,点到门框的距离,则的长为 cm.
三、解答题
19.如图,梯形ABCD是某水库大坝的横断面,其坝顶宽5米,坝底宽33米,坝的迎水坡度是i1=1:2,背水坡的坡度i2=2:3,求:水坝横截面的面积.
20.如图,小明一家从家所在地自驾前往古镇游玩,古镇在小明家的正北方向千米处,由于道路清障,小明一家先从沿西北方向行驶至地,再从地沿北偏东方向行驶至古镇,求小明一家从地到地实际行驶的路程是多少千米?(结果精确到千米)
(参考数据:,,,)
21.如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东方向上.(参考数据:,,,.)
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
22.如图,在数学综合实践活动课上,两名同学要测量小河对岸大树的高度,甲同学在点测得大树顶端的仰角为,乙同学从点出发沿斜坡走米到达斜坡上点处,在此处测得大树顶端的仰角为,且斜坡的坡度为,于点,点、、在一条直线上.
(1)求乙同学从点到点的过程中,上升的竖直高度;
(2)依据他们测量的数据求出大树的高度.(参考数据:)
23.如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为,细绳在右侧达到最高点时与一个水平放置的挡板所成的角度为.(参考数据:)
(1)求小球达到最高点位置与最低点位置时的高度差.
(2)求这段细绳的长度.
24.如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC、CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
25.图1是某区规划建设的过街天桥的侧面示意图,等腰梯形ABCD的上底BC表示主跨桥,两腰AB,CD表示桥两侧的斜梯,A,D两点在地面上,已知AD=40m,设计桥高为4m,设计斜梯的坡度为1:2.4.点A左侧25m点P处有一棵古树,有关部门划定了以P为圆心,半径为3m的圆形保护区.
(1)求主跨桥与桥两侧斜梯的长度之和;
(2)为了保证桥下大货车的安全通行,桥高要增加到5m,同时为了方便自行车及电动车上桥,新斜梯的坡度要减小到1:4,新方案主跨桥的水平位置和长度保持不变.另外,新方案要修建一个缓坡MN作为轮椅坡道,坡道终点N在左侧的新斜梯上,并在点N处安装无障碍电梯,坡道起点M在AP上,且不能影响到古树的圆形保护区.已知点N距离地面的高度为0.9m,请利用表中的数据,通过计算判断轮椅坡道的设计是否可行.
表:轮椅坡道的最大高度和水平长度
坡度 1:20 1:16 1:12 1:10 1:8
最大高度(m) 1.20 0.90 0.75 0.60 0.30
水平长度(m) 24.00 14.40 9.00 6.00 2.40
26.钓鱼伞设计:户外钓鱼是一项独特的休闲娱乐活动,已经吸引了越来越多的人.
图解:图1是某钓鱼俱乐部设计了一款新型钓伞,伞面可近似看成弧线.图2是其侧面示意图.已知遮阳伞由伞面弧、支架和支架组成,D为两个支架的连接点,其中支架垂直于且可在D处任意旋转,C为中点,支架垂直于地面且可以适当调整长度.传统的钓伞在连接点D处需要手动旋转支架,使弦与光线垂直以达到最大遮阳目的.新型遮阳伞在D处设置了光线传感器,自动旋转支架以保持始终与光线垂直.图3-5为在不同太阳高度下的情况,其中为光线方向,为在地面形成的影子.仅考虑光线由右上到左下的情况.
定义变量:设米,米,米,太阳高度角定义为光线与地面夹角(为锐角).
问题一:如图4,若,当伞面端点的影子刚好与点重合时,求影子的长度.
问题二:根据图3-图5,为了最大程度利用遮阳伞,假设钓鱼人坐在点,面朝阳光方向,设的距离为米,请利用相关变量表示.
问题三:在图5中,该俱乐部的某场钓鱼比赛定在上午九点,此时太阳光线与地面夹角为,俱乐部选择,型号的钓伞.假设点刚好在岸边,座椅在处,为了满足最大舒适性,选手距离岸边距离(在点左侧)不超过米,且为了满足视野不影响比赛,要求点离地面的垂直距离不小于米,根据此要求,该俱乐部应如何设置的高度以满足比赛,求的取值范围.(精确到0.1米,参考数据:)
答案
一、单选题
1.D
【分析】本题考查了解直角三角形的应用坡度坡角问题.根据坡角的正切坡度,列式可得结果.
【解析】解:设这个斜坡的坡角为,
由题意得:,
.
故选:D.
2.B
【分析】本题考查了解直角三角形,仰角俯角,熟练掌握锐角三角函数的定义是解答本题的关键.
根据题意,得到,利用已知角的正弦,求出答案.
【解析】解:如图,在中,
米,,
,
(米),
故选:.
3.A
【分析】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
根据图形和锐角三角函数,可以表示出的值.
【解析】解:∵,
米,
故选:A.
4.B
【分析】本题考查了俯角的定义,根据俯角是往下看,观测者的视线与水平线的夹角即为俯角,结合图形,即可求解.
【解析】解:∵直线为水平线,,
∴从甲楼的楼顶处观测乙楼的楼顶处的俯角是,
故选:B.
5.C
【分析】此题考查了仰角问题,过作于点,则四边形是矩形,根据性质和三角函数即可求解,解题的关键是添加辅助线构造直角三角形,熟练掌握三角函数的应用.
【解析】如图,过作于点,
则有四边形是矩形,
∴米,米,,
在中,,
∴,
∴,
故选:.
6.B
【分析】根据直角三角形的三角函数得出,进而得出,利用勾股定理得出即可.
【解析】解:如图:
,
,
千米,
千米,千米,
千米,
千米,
故选B.
7.D
【分析】此题考查了解直角三角形的应用,三角函数的基本概念,
当小球在最高位置时,过小球作小球位置最低时细绳的垂线,在构建的直角三角形中,可根据偏转角的度数和细绳的长度,求出小球最低位置时的铅直高度,进而可求出小球在最高位置与最低位置时的高度差.
【解析】解:如图:过作于,
中,厘米,,
.
(厘米).
故选:D.
8.A
【分析】过点P作于点C,则这条河的宽度是的长,根据锐角三角函数可得,从而得到,即可求解.
【解析】解:如图,过点P作于点C,则这条河的宽度是的长,
∵,
∴,
∵米,
∴,
即,
∴,
即米,
即这条河的宽度是米,
故选:A.
9.B
【分析】过点C作CN⊥AB,交AB于M,通过构建直角三角形解答即可.
【解析】解:过点C作CN⊥AB,交AB于M,交地面于N
由题意可知MN=30cm,当CN=90cm时,CM=60cm,
∵Rt△BCM中,∠ABE=70°,sin∠ABE=sin70°=≈0.9,
∴BC≈67cm,
∴CEBC BE=67 40=27cm.
故选B.
10.B
【分析】此题考查了解直角三角形的应用仰角俯角问题、坡度坡角问题,由坡度的定义和勾股定理得出的长,再由等腰直角三角形的性质得出的长,然后由锐角三角函数定义求出的长,即可得出答案,正确作出辅助线构造直角三角形是解题的关键.
【解析】解:如图,过点作于,过作于,
则,
∵,
∴设米,则米,
∴米,
∵米,
∴,
解得,
∴,
∴米,
∵,
∴是等腰直角三角形,
∴米,
在中,,
∴米,
∴米,
故选:.
二、填空题
11.60
【分析】设斜坡的高3x米,水平宽度为4x米,根据勾股定理计算即可.
【解析】解: ∵斜坡坡度为3:4,
∴设斜坡的高3x米,水平宽度为4x米,
由勾股定理得,(3x)2+(4x)2=1002,
解得,x=20,
即斜坡的高为3×20=60(米),
故答案为:60.
12.
【分析】本题考查了解直角三角形的仰角俯角问题,首先过点A作于点D,根据题意得,,米,然后利用三角函数求解即可求得答案.
【解析】解:首先过点A作于点D,如下图所示,
则,,米,
在中,米,
在中,米,
∴米.
故答案为:
13.5
【分析】本题考查含的直角三角形知识,掌握所对的直角边是斜边的一半是解题的关键.含角的直角三角形,利用直角三角形中角所对的直角边是斜边的一半即可求解.
【解析】解: 垂直于横梁,,.
.
故答案为:5.
14.1200
【分析】根据题意,作出合适的辅助线,然后根据锐角三角函数即可表示出此时飞机离地面的高度.
【解析】解:作交于点,如图所示,
,,
,
,
,
故答案为:1200.
15.
【分析】过A点作AD⊥BC交BC于D点,根据题意得到四边形APBD是正方形,求出DB的长度,然后根据仰角β=60°的三角函数值和AD=30求出DC的长度,即可求出大楼的楼高BC的长度.
【解析】解:如图所示,过A点作AD⊥BC交BC于D点,
∵,,,
∴四边形APBD是矩形,
又∵,
∴,
∴,
∴四边形APBD是正方形,
∴,
∵,
∴,
∴.
故答案为:.
16.米
【分析】作于点E,作于点F,由得米,由AB=57知米,由四边形BCEF是矩形知米,由知米,从而得到 米.
【解析】过点D作于点E,作于点F,
由题可得:
AB=57,DE=30,,,
在Rt△ADE中,,
∴,
∴,
∵AB=50,
∴,
∵四边形BCEF是矩形,
∴,
在Rt△DCF中,,
∴,
∴,
∴米.
故答案为米.
17.
【分析】本题考查了解直角三角形的应用坡度坡角问题,解直角三角形,求出,再解直角三角形,求出,最后根据线段的和差关系即可求解,正确作出辅助线是解题的关键.
【解析】解:延长交于点,
∵,
∴,
∵ ,
∴,,
∵,点是的中点,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
∴平台的长约为,
故答案为:.
18.
【分析】过作,为垂足,利用三角函数和勾股定理求出、即可求解;连接,作,为垂足,为的对应点,设,分别表示出、、、,用勾股定理即可求解.
【解析】
解:过作,为垂足,
,
,
,
,
,
,
.
故答案:.
解:如图,连接,作,为垂足,为的对应点,
,
,
,
,
设,则,
,
由题空1得:,,
,
又
,
,
即:,
整理得:,
解得:,(舍去),
.
故答案:.
三、解答题
19.∵i1=1:2,背水坡的坡度i2=2:3
设AE=DF=2x米,则BE=4x米,CF=3x米
∵AD=5米
∴EF=5米
∵BC=33米
∴AE=8米
∴水坝横截面的面积为平方米.
20.解:如图所示,过点作于点,
∵点在点的西北方向,
∴,
∴,,
∵点在点的北偏东方向,
∴,
∵,
设,则,,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∴(千米)
答:从地到地实际行驶的路程是千米.
21.(1)解:过点M作,交AC的延长线于D,设.
∵在中,,
又∵在中,,
∴,
∵,
∴.
∴(米).
即轮船M到海岸线l的距离约为167.79米.
(2)解:作,交l于点F.
在中,有:(米),
∴.
∴该轮船能行至码头靠岸.
22.(1)解:根据题意,在中,
∵,
∴,
∵,
∴,
∴米.
∴乙同学从点到点的过程中,上升的竖直高度为米.
(2)解:如图,过点作于点,设米,
在中,,
∴米,
由(1)得米,
在矩形中,米,
米,
在中,米,
∵,且,
∴,解方程得,米,
∴大树的高度为米.
23.(1)解:连接交于点, 可知,
由题意可得则
故之间的高度差为;
(2)由 知, 的高度差也是,
故,
解得:
则
答: 这段细绳的长度为.
24.解:(1)如图2中,作BO⊥DE于O.
∵∠OEA=∠BOE=∠BAE=90°,
∴四边形ABOE是矩形,
∴∠OBA=90°,
∴∠DBO=150°﹣90°=60°,
∴OD=BD sin60°=20(cm),
∴DE=OD+OE=OD+AB=(20+5)cm;
(2)过C作CG⊥BH,CK⊥DE,
由题意得,BC=CD=20m,CG=KH,
∴在Rt△CGB中,sin∠CBH=,
∴CG=10cm,
∴KH=10cm,
∵∠BCG=90°﹣60°=30°,
∴∠DCK=150°﹣90°﹣30°=30°,
在Rt△DCK中,sin∠DCK===,
∴DK=10cm,
∴此时连杆端点D离桌面l的高度为10+10+5=(15+10)cm
∴比原来降低了(20+5)﹣(15+10)=10﹣10,
答:比原来降低了(10﹣10)厘米.
25.(1)解:如图,作直线AD,则AD过点 和点,过点B、C分别作BE⊥AD,CF⊥AD,垂足为E、F,延长EB,延长FC,则射线EB过点,射线FC过点,由题意得,BE=CF=4m,AP=25m,E=5m,
∵斜坡AB的坡度为1:2.4,即=1:2.4,
∴AE=4×2.4=9.6(m),
又∵四边形ABCD是等腰梯形,
∴AE=DF=9.6m,
∴BC=AD﹣AE﹣DF=5.8(m),
AB===10.4(m)=CD,
∴主跨桥与桥两侧斜梯的长度之和为AB+BC+CD=10.4+5.8+10.4=26.6(m),
答:主跨桥与桥两侧斜梯的长度之和为26.6m.
(2)解:∵斜坡的坡度为1:4,即=1:4,
∴E=5×4=20(m),
∴A=20﹣9.6=11.4(m),
G=4NG=4×0.9=3.6(m),
∴AG=11.4﹣3.6=7.8(m),
点M到点G的最多距离MG=25﹣7.8﹣3=14.2(m),
∵14.2<14.4,
∴轮椅坡道的设计不可行.
26.问题一
解:当点E和点N重合时,过点D作,交于点F,过点N作,交于点H,
,
,
四边形为矩形,米,
,
,
由题可知,米,米,
在中,由勾股定理得米,
则,
在中,,
解得米,即影长为米,
问题二
解:
延长交于点,
,
,即,
中,,则,
,
在中,,
,则,
当点N在点E右侧时,,
则,
当点N在点E左侧时,,
则,
当点N与点E重合时,,即,
综上所述,;
问题三
解:过点F作,交于P,过点B作交延长线于Q,交延长线于R,
当时,都为等腰直角三角形,
,
,
,
,
,
,
由题可知:,
,
当时,解得:
,
即.
一、单选题
1.如果斜坡的坡度为,那么这条斜坡的坡角为( )
A.75度 B.60度 C.45度 D.30度
2.进博会期间,从一架离地米的无人机上,测得地面监测点的俯角是,那么此时无人机与地面监测点的距离是( )
A.米 B.米 C.米 D.米
3.许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图,的长为50米,与的夹角为,则高是()
A.米 B.米 C.米 D.米
4.如图,已知直线为水平线,,从甲楼的楼顶处观测乙楼的楼顶处的俯角是( )
A. B. C. D.
5.如图,为了测量学校教学楼的高度,在操场的处架起测角仪,测角仪的高米,从点测得教学大楼顶端的仰角为,测角仪底部到大楼底部的距离是米,那么教学大楼的高是( )
A. B.
C. D.
6.如图,一艘船从处向北偏东的方向行驶千米到处,再从处向正西方向行驶千米到处,这时这艘船与的距离( )
A.千米 B.千米 C.1千米 D.千米
7.如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在左、右两个最高位置时,细绳相应所成的角∠AOB为40°,那么小球在最高位置和最低位置时的高度差为( )
A.厘米 B.厘米
C.厘米 D.厘米
8.如图,为测量一条河的宽度,分别在河岸一边相距米的、两点处,观测对岸的标志物,测得、,那么这条河的宽度是( )
A.米 B.米
C.米 D.米
9.共享单车为市民出行提供了便利.图1为单车实物图,图2为单车示意图,与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线方向调节.已知,,,车轮半径为,,小明体验后觉得当坐垫C离地面高度为时骑着比较舒适,此时的长约为( )(结果精确到,参考数据:,,)
A. B. C. D.
10.某同学利用数学知识测量建筑物的高度,他从点出发沿着坡度为的斜坡步行米到达点处,用测角仪测得建筑物顶端的仰角为,建筑物底端的俯角为.若为水平的地面,点在同一平面内,建筑物和测角仪与水平方向垂直,若米,则此建筑物的高度约为( )(精确到米,参考数据:,,)
A.米 B.米 C.米 D.米
二、填空题
11.已知斜坡坡度为,如果斜坡长为米,那么斜坡的高为 米.
12.如图,热气球的探测器显示,从热气球A处看一栋楼顶部B的仰角为,看这栋楼底部C的俯角为,热气球A处与楼的水平距离为m米,那么这栋楼的高度为 米.(用含的式子表示)
13.如图是屋架设计图的一部分,立柱垂直于横梁,如果,,那么立柱的长度是 米.
14.如图,一架飞机在点A处测得水平地面上一个标志物M的俯角为α,tanα=,水平飞行900米后,到达点B处,又测得标志物M的俯角为β,tanβ=,那么此时飞机离地面的高度为 米.
15.如图,某兴趣小组用无人机对大楼进行测高,无人机从距离大楼30米(PB=30米)垂直起飞,飞到A处悬停,测得大楼底部俯角α=45°,大楼顶部仰角β=60°,则大楼的楼高BC= 米.(结果保留根号)
16.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的处,无人机测得操控者的俯角为,测得点处的俯角为.又经过人工测量操控者和教学楼距离为米,则教学楼的高度为 .(点都在同一平面上,结果保留根号)
17.如图,已知斜坡长为,坡角(即)为,,现计划在斜坡中点处挖去部分坡体(用阴影表示)修建一个平行于水平线的平台和一条新的斜坡.若修建的斜坡的坡角为,则平台的长为 .(参考数据:)
18.一款闭门器按如图1所示安装,支点,分别固定在门框和门板上,门宽,摇臂,连杆,闭门器工作时,摇臂、连杆和长度均固定不变.如图2,当门闭合时,,则的长为 cm.如图3,门板绕点旋转,当∠B=90°时,点到门框的距离,则的长为 cm.
三、解答题
19.如图,梯形ABCD是某水库大坝的横断面,其坝顶宽5米,坝底宽33米,坝的迎水坡度是i1=1:2,背水坡的坡度i2=2:3,求:水坝横截面的面积.
20.如图,小明一家从家所在地自驾前往古镇游玩,古镇在小明家的正北方向千米处,由于道路清障,小明一家先从沿西北方向行驶至地,再从地沿北偏东方向行驶至古镇,求小明一家从地到地实际行驶的路程是多少千米?(结果精确到千米)
(参考数据:,,,)
21.如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东方向上.(参考数据:,,,.)
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
22.如图,在数学综合实践活动课上,两名同学要测量小河对岸大树的高度,甲同学在点测得大树顶端的仰角为,乙同学从点出发沿斜坡走米到达斜坡上点处,在此处测得大树顶端的仰角为,且斜坡的坡度为,于点,点、、在一条直线上.
(1)求乙同学从点到点的过程中,上升的竖直高度;
(2)依据他们测量的数据求出大树的高度.(参考数据:)
23.如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在A、B两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为,细绳在右侧达到最高点时与一个水平放置的挡板所成的角度为.(参考数据:)
(1)求小球达到最高点位置与最低点位置时的高度差.
(2)求这段细绳的长度.
24.如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC、CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
25.图1是某区规划建设的过街天桥的侧面示意图,等腰梯形ABCD的上底BC表示主跨桥,两腰AB,CD表示桥两侧的斜梯,A,D两点在地面上,已知AD=40m,设计桥高为4m,设计斜梯的坡度为1:2.4.点A左侧25m点P处有一棵古树,有关部门划定了以P为圆心,半径为3m的圆形保护区.
(1)求主跨桥与桥两侧斜梯的长度之和;
(2)为了保证桥下大货车的安全通行,桥高要增加到5m,同时为了方便自行车及电动车上桥,新斜梯的坡度要减小到1:4,新方案主跨桥的水平位置和长度保持不变.另外,新方案要修建一个缓坡MN作为轮椅坡道,坡道终点N在左侧的新斜梯上,并在点N处安装无障碍电梯,坡道起点M在AP上,且不能影响到古树的圆形保护区.已知点N距离地面的高度为0.9m,请利用表中的数据,通过计算判断轮椅坡道的设计是否可行.
表:轮椅坡道的最大高度和水平长度
坡度 1:20 1:16 1:12 1:10 1:8
最大高度(m) 1.20 0.90 0.75 0.60 0.30
水平长度(m) 24.00 14.40 9.00 6.00 2.40
26.钓鱼伞设计:户外钓鱼是一项独特的休闲娱乐活动,已经吸引了越来越多的人.
图解:图1是某钓鱼俱乐部设计了一款新型钓伞,伞面可近似看成弧线.图2是其侧面示意图.已知遮阳伞由伞面弧、支架和支架组成,D为两个支架的连接点,其中支架垂直于且可在D处任意旋转,C为中点,支架垂直于地面且可以适当调整长度.传统的钓伞在连接点D处需要手动旋转支架,使弦与光线垂直以达到最大遮阳目的.新型遮阳伞在D处设置了光线传感器,自动旋转支架以保持始终与光线垂直.图3-5为在不同太阳高度下的情况,其中为光线方向,为在地面形成的影子.仅考虑光线由右上到左下的情况.
定义变量:设米,米,米,太阳高度角定义为光线与地面夹角(为锐角).
问题一:如图4,若,当伞面端点的影子刚好与点重合时,求影子的长度.
问题二:根据图3-图5,为了最大程度利用遮阳伞,假设钓鱼人坐在点,面朝阳光方向,设的距离为米,请利用相关变量表示.
问题三:在图5中,该俱乐部的某场钓鱼比赛定在上午九点,此时太阳光线与地面夹角为,俱乐部选择,型号的钓伞.假设点刚好在岸边,座椅在处,为了满足最大舒适性,选手距离岸边距离(在点左侧)不超过米,且为了满足视野不影响比赛,要求点离地面的垂直距离不小于米,根据此要求,该俱乐部应如何设置的高度以满足比赛,求的取值范围.(精确到0.1米,参考数据:)
答案
一、单选题
1.D
【分析】本题考查了解直角三角形的应用坡度坡角问题.根据坡角的正切坡度,列式可得结果.
【解析】解:设这个斜坡的坡角为,
由题意得:,
.
故选:D.
2.B
【分析】本题考查了解直角三角形,仰角俯角,熟练掌握锐角三角函数的定义是解答本题的关键.
根据题意,得到,利用已知角的正弦,求出答案.
【解析】解:如图,在中,
米,,
,
(米),
故选:.
3.A
【分析】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
根据图形和锐角三角函数,可以表示出的值.
【解析】解:∵,
米,
故选:A.
4.B
【分析】本题考查了俯角的定义,根据俯角是往下看,观测者的视线与水平线的夹角即为俯角,结合图形,即可求解.
【解析】解:∵直线为水平线,,
∴从甲楼的楼顶处观测乙楼的楼顶处的俯角是,
故选:B.
5.C
【分析】此题考查了仰角问题,过作于点,则四边形是矩形,根据性质和三角函数即可求解,解题的关键是添加辅助线构造直角三角形,熟练掌握三角函数的应用.
【解析】如图,过作于点,
则有四边形是矩形,
∴米,米,,
在中,,
∴,
∴,
故选:.
6.B
【分析】根据直角三角形的三角函数得出,进而得出,利用勾股定理得出即可.
【解析】解:如图:
,
,
千米,
千米,千米,
千米,
千米,
故选B.
7.D
【分析】此题考查了解直角三角形的应用,三角函数的基本概念,
当小球在最高位置时,过小球作小球位置最低时细绳的垂线,在构建的直角三角形中,可根据偏转角的度数和细绳的长度,求出小球最低位置时的铅直高度,进而可求出小球在最高位置与最低位置时的高度差.
【解析】解:如图:过作于,
中,厘米,,
.
(厘米).
故选:D.
8.A
【分析】过点P作于点C,则这条河的宽度是的长,根据锐角三角函数可得,从而得到,即可求解.
【解析】解:如图,过点P作于点C,则这条河的宽度是的长,
∵,
∴,
∵米,
∴,
即,
∴,
即米,
即这条河的宽度是米,
故选:A.
9.B
【分析】过点C作CN⊥AB,交AB于M,通过构建直角三角形解答即可.
【解析】解:过点C作CN⊥AB,交AB于M,交地面于N
由题意可知MN=30cm,当CN=90cm时,CM=60cm,
∵Rt△BCM中,∠ABE=70°,sin∠ABE=sin70°=≈0.9,
∴BC≈67cm,
∴CEBC BE=67 40=27cm.
故选B.
10.B
【分析】此题考查了解直角三角形的应用仰角俯角问题、坡度坡角问题,由坡度的定义和勾股定理得出的长,再由等腰直角三角形的性质得出的长,然后由锐角三角函数定义求出的长,即可得出答案,正确作出辅助线构造直角三角形是解题的关键.
【解析】解:如图,过点作于,过作于,
则,
∵,
∴设米,则米,
∴米,
∵米,
∴,
解得,
∴,
∴米,
∵,
∴是等腰直角三角形,
∴米,
在中,,
∴米,
∴米,
故选:.
二、填空题
11.60
【分析】设斜坡的高3x米,水平宽度为4x米,根据勾股定理计算即可.
【解析】解: ∵斜坡坡度为3:4,
∴设斜坡的高3x米,水平宽度为4x米,
由勾股定理得,(3x)2+(4x)2=1002,
解得,x=20,
即斜坡的高为3×20=60(米),
故答案为:60.
12.
【分析】本题考查了解直角三角形的仰角俯角问题,首先过点A作于点D,根据题意得,,米,然后利用三角函数求解即可求得答案.
【解析】解:首先过点A作于点D,如下图所示,
则,,米,
在中,米,
在中,米,
∴米.
故答案为:
13.5
【分析】本题考查含的直角三角形知识,掌握所对的直角边是斜边的一半是解题的关键.含角的直角三角形,利用直角三角形中角所对的直角边是斜边的一半即可求解.
【解析】解: 垂直于横梁,,.
.
故答案为:5.
14.1200
【分析】根据题意,作出合适的辅助线,然后根据锐角三角函数即可表示出此时飞机离地面的高度.
【解析】解:作交于点,如图所示,
,,
,
,
,
故答案为:1200.
15.
【分析】过A点作AD⊥BC交BC于D点,根据题意得到四边形APBD是正方形,求出DB的长度,然后根据仰角β=60°的三角函数值和AD=30求出DC的长度,即可求出大楼的楼高BC的长度.
【解析】解:如图所示,过A点作AD⊥BC交BC于D点,
∵,,,
∴四边形APBD是矩形,
又∵,
∴,
∴,
∴四边形APBD是正方形,
∴,
∵,
∴,
∴.
故答案为:.
16.米
【分析】作于点E,作于点F,由得米,由AB=57知米,由四边形BCEF是矩形知米,由知米,从而得到 米.
【解析】过点D作于点E,作于点F,
由题可得:
AB=57,DE=30,,,
在Rt△ADE中,,
∴,
∴,
∵AB=50,
∴,
∵四边形BCEF是矩形,
∴,
在Rt△DCF中,,
∴,
∴,
∴米.
故答案为米.
17.
【分析】本题考查了解直角三角形的应用坡度坡角问题,解直角三角形,求出,再解直角三角形,求出,最后根据线段的和差关系即可求解,正确作出辅助线是解题的关键.
【解析】解:延长交于点,
∵,
∴,
∵ ,
∴,,
∵,点是的中点,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
∴平台的长约为,
故答案为:.
18.
【分析】过作,为垂足,利用三角函数和勾股定理求出、即可求解;连接,作,为垂足,为的对应点,设,分别表示出、、、,用勾股定理即可求解.
【解析】
解:过作,为垂足,
,
,
,
,
,
,
.
故答案:.
解:如图,连接,作,为垂足,为的对应点,
,
,
,
,
设,则,
,
由题空1得:,,
,
又
,
,
即:,
整理得:,
解得:,(舍去),
.
故答案:.
三、解答题
19.∵i1=1:2,背水坡的坡度i2=2:3
设AE=DF=2x米,则BE=4x米,CF=3x米
∵AD=5米
∴EF=5米
∵BC=33米
∴AE=8米
∴水坝横截面的面积为平方米.
20.解:如图所示,过点作于点,
∵点在点的西北方向,
∴,
∴,,
∵点在点的北偏东方向,
∴,
∵,
设,则,,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∴(千米)
答:从地到地实际行驶的路程是千米.
21.(1)解:过点M作,交AC的延长线于D,设.
∵在中,,
又∵在中,,
∴,
∵,
∴.
∴(米).
即轮船M到海岸线l的距离约为167.79米.
(2)解:作,交l于点F.
在中,有:(米),
∴.
∴该轮船能行至码头靠岸.
22.(1)解:根据题意,在中,
∵,
∴,
∵,
∴,
∴米.
∴乙同学从点到点的过程中,上升的竖直高度为米.
(2)解:如图,过点作于点,设米,
在中,,
∴米,
由(1)得米,
在矩形中,米,
米,
在中,米,
∵,且,
∴,解方程得,米,
∴大树的高度为米.
23.(1)解:连接交于点, 可知,
由题意可得则
故之间的高度差为;
(2)由 知, 的高度差也是,
故,
解得:
则
答: 这段细绳的长度为.
24.解:(1)如图2中,作BO⊥DE于O.
∵∠OEA=∠BOE=∠BAE=90°,
∴四边形ABOE是矩形,
∴∠OBA=90°,
∴∠DBO=150°﹣90°=60°,
∴OD=BD sin60°=20(cm),
∴DE=OD+OE=OD+AB=(20+5)cm;
(2)过C作CG⊥BH,CK⊥DE,
由题意得,BC=CD=20m,CG=KH,
∴在Rt△CGB中,sin∠CBH=,
∴CG=10cm,
∴KH=10cm,
∵∠BCG=90°﹣60°=30°,
∴∠DCK=150°﹣90°﹣30°=30°,
在Rt△DCK中,sin∠DCK===,
∴DK=10cm,
∴此时连杆端点D离桌面l的高度为10+10+5=(15+10)cm
∴比原来降低了(20+5)﹣(15+10)=10﹣10,
答:比原来降低了(10﹣10)厘米.
25.(1)解:如图,作直线AD,则AD过点 和点,过点B、C分别作BE⊥AD,CF⊥AD,垂足为E、F,延长EB,延长FC,则射线EB过点,射线FC过点,由题意得,BE=CF=4m,AP=25m,E=5m,
∵斜坡AB的坡度为1:2.4,即=1:2.4,
∴AE=4×2.4=9.6(m),
又∵四边形ABCD是等腰梯形,
∴AE=DF=9.6m,
∴BC=AD﹣AE﹣DF=5.8(m),
AB===10.4(m)=CD,
∴主跨桥与桥两侧斜梯的长度之和为AB+BC+CD=10.4+5.8+10.4=26.6(m),
答:主跨桥与桥两侧斜梯的长度之和为26.6m.
(2)解:∵斜坡的坡度为1:4,即=1:4,
∴E=5×4=20(m),
∴A=20﹣9.6=11.4(m),
G=4NG=4×0.9=3.6(m),
∴AG=11.4﹣3.6=7.8(m),
点M到点G的最多距离MG=25﹣7.8﹣3=14.2(m),
∵14.2<14.4,
∴轮椅坡道的设计不可行.
26.问题一
解:当点E和点N重合时,过点D作,交于点F,过点N作,交于点H,
,
,
四边形为矩形,米,
,
,
由题可知,米,米,
在中,由勾股定理得米,
则,
在中,,
解得米,即影长为米,
问题二
解:
延长交于点,
,
,即,
中,,则,
,
在中,,
,则,
当点N在点E右侧时,,
则,
当点N在点E左侧时,,
则,
当点N与点E重合时,,即,
综上所述,;
问题三
解:过点F作,交于P,过点B作交延长线于Q,交延长线于R,
当时,都为等腰直角三角形,
,
,
,
,
,
,
由题可知:,
,
当时,解得:
,
即.
