沪教版九年级数学上册 第二十五章《锐角的三角比》单元复习检测卷(含解析)
文档属性
| 名称 | 沪教版九年级数学上册 第二十五章《锐角的三角比》单元复习检测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 11:07:00 | ||
图片预览

文档简介
第二十五章《锐角的三角比》单元复习检测卷
一、单选题
1.如果,那么与的差( ).
A.大于 B.小于 C.等于 D.不能确定
2.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
3.如图,在矩形中,为边上一点,将沿直线翻折,使得点的对应点落在边上.若,则的长度是( )
A. B. C. D.1
4.如图,某大楼DE楼顶挂着“众志成城,抗击疫情”的大型宣传牌,为了测量宣传牌的高度CD,小江从楼底点E向前行走30米到达点A,在A处测得宣传牌下端D的仰角为60°.小江再沿斜坡AB行走26米到达点B,在点B测得宣传牌的上端C的仰角为43°,已知斜坡AB的坡度i=1:2.4,点A、B、C、D、E在同一平面内,CD⊥AE,宣传牌CD的高度约为( )(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,≈1.73)
A.8.3米 B.8.5米 C.8.7米 D.8.9米
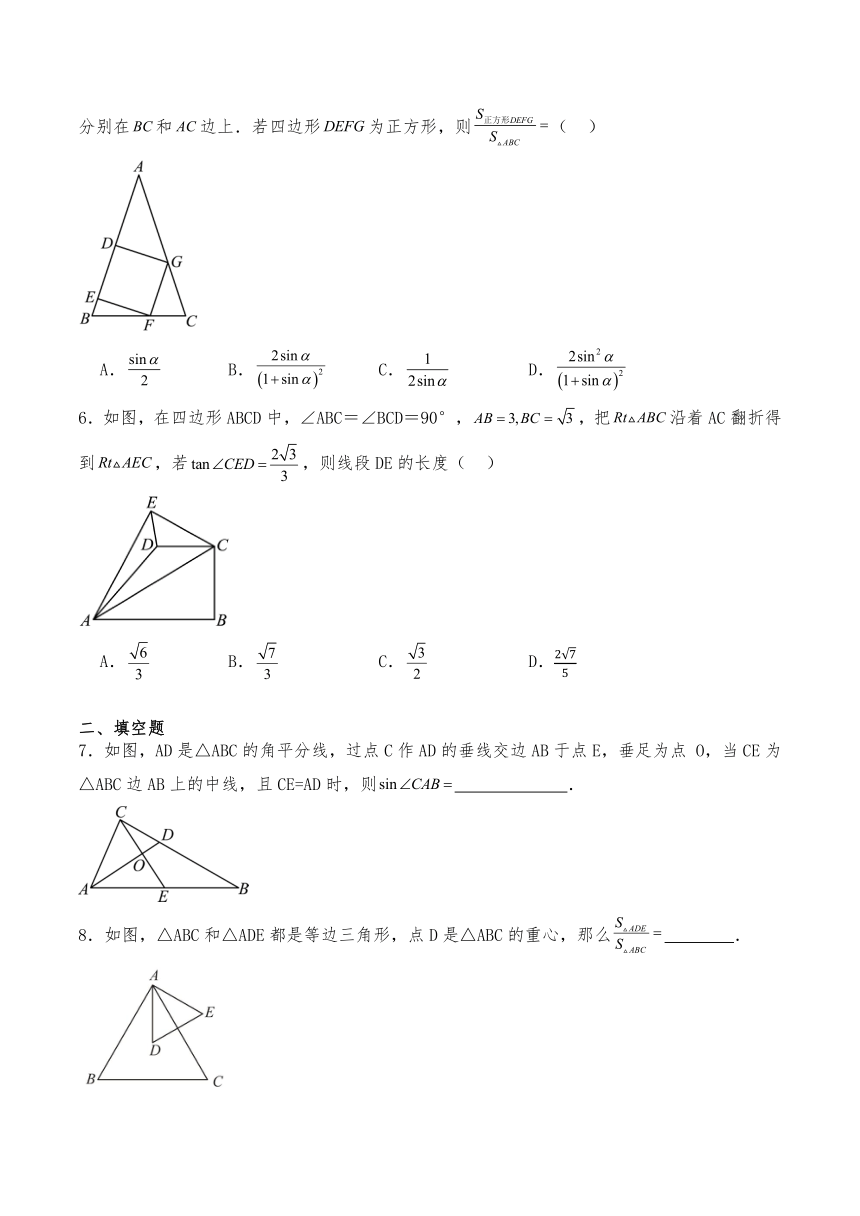
5.如图,在等腰三角形中.,.点D,E在边上,点F,G分别在和边上.若四边形为正方形,则( )
A. B. C. D.
6.如图,在四边形ABCD中,∠ABC=∠BCD=90°,,把沿着AC翻折得到,若,则线段DE的长度( )
A. B. C. D.
二、填空题
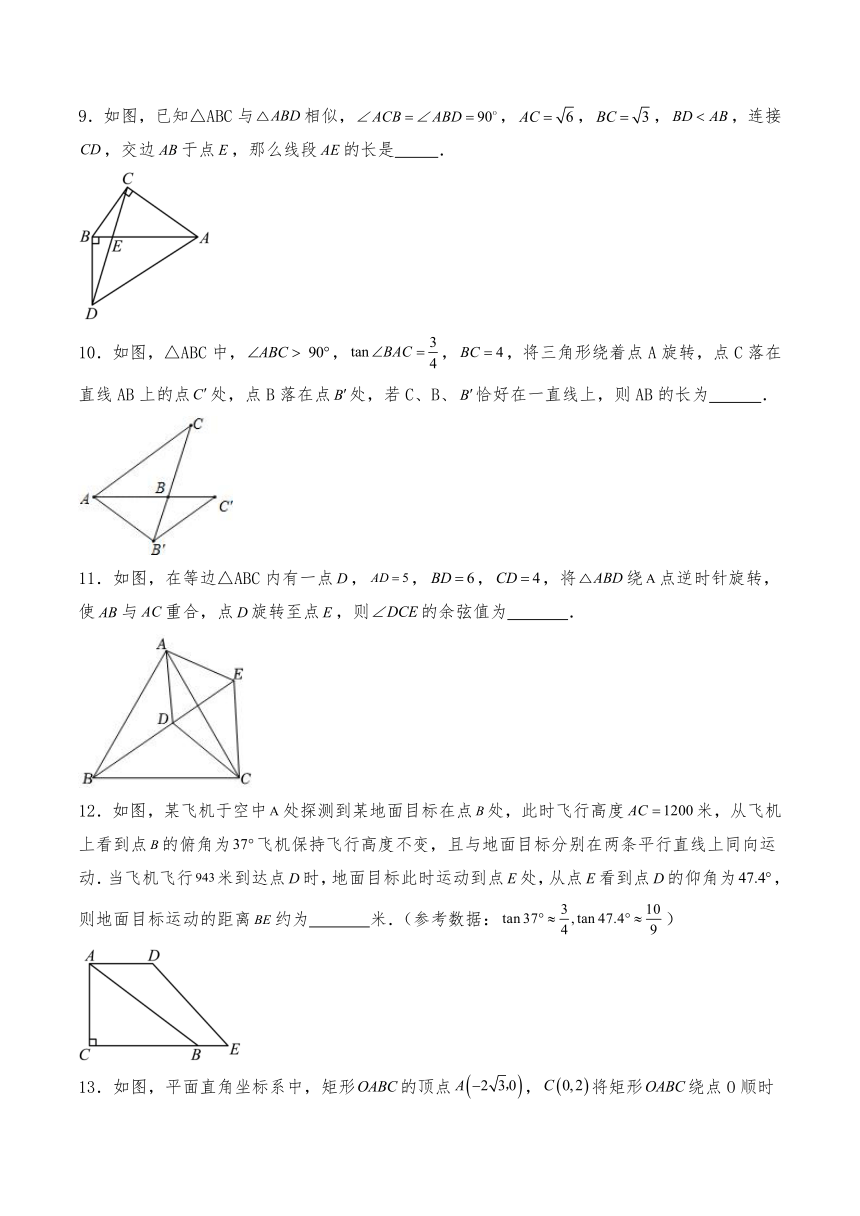
7.如图,AD是△ABC的角平分线,过点C作AD的垂线交边AB于点E,垂足为点 O,当CE为△ABC边AB上的中线,且CE=AD时,则 .
8.如图,△ABC和△ADE都是等边三角形,点D是△ABC的重心,那么 .
9.如图,已知△ABC与相似,,,,,连接,交边于点,那么线段的长是 .
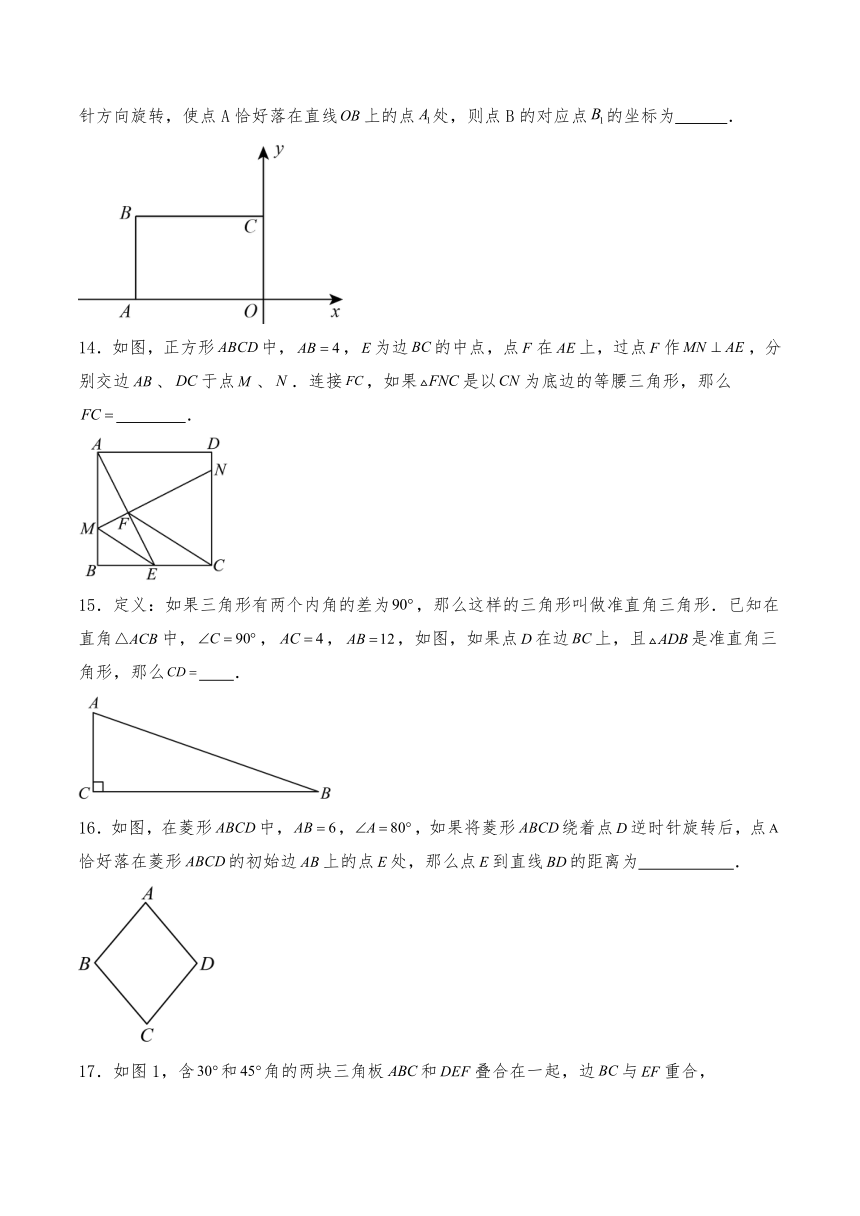
10.如图,△ABC中,,,,将三角形绕着点A旋转,点C落在直线AB上的点处,点B落在点处,若C、B、恰好在一直线上,则AB的长为 .
11.如图,在等边△ABC内有一点,,,,将绕点逆时针旋转,使与重合,点旋转至点,则的余弦值为 .
12.如图,某飞机于空中处探测到某地面目标在点处,此时飞行高度米,从飞机上看到点的俯角为飞机保持飞行高度不变,且与地面目标分别在两条平行直线上同向运动.当飞机飞行米到达点时,地面目标此时运动到点处,从点看到点的仰角为,则地面目标运动的距离约为 米.(参考数据:)
13.如图,平面直角坐标系中,矩形的顶点,将矩形绕点O顺时针方向旋转,使点A恰好落在直线上的点处,则点B的对应点的坐标为 .
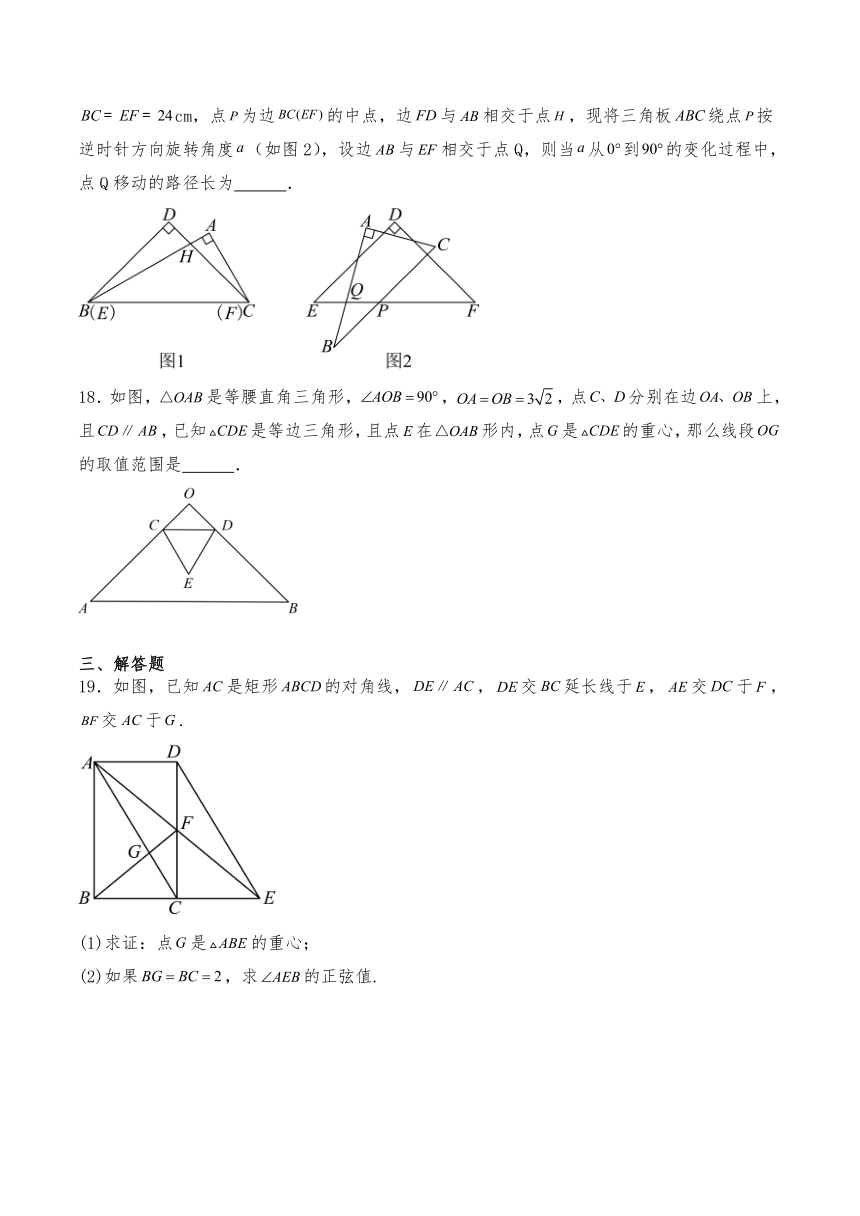
14.如图,正方形中,,为边的中点,点在上,过点作,分别交边、于点、.连接,如果是以为底边的等腰三角形,那么 .
15.定义:如果三角形有两个内角的差为,那么这样的三角形叫做准直角三角形.已知在直角中,,,,如图,如果点在边上,且是准直角三角形,那么 .
16.如图,在菱形中,,,如果将菱形绕着点逆时针旋转后,点恰好落在菱形的初始边上的点处,那么点到直线的距离为 .
17.如图1,含和角的两块三角板和叠合在一起,边与重合,cm,点为边的中点,边与相交于点,现将三角板绕点按逆时针方向旋转角度(如图2),设边与相交于点Q,则当从到的变化过程中,点Q移动的路径长为 .
18.如图,是等腰直角三角形,,,点分别在边上,且,已知是等边三角形,且点在形内,点是的重心,那么线段的取值范围是 .
三、解答题
19.如图,已知是矩形的对角线,,交延长线于,交于,交于.
(1)求证:点是的重心;
(2)如果,求的正弦值.
20.如图,在中,,,垂足为点D,,垂足为点,和相交于点.过点A作,交边延长线于点,点是边上一点,.
(1)求证:;
(2)求证:.
21.小明为测量河对岸大楼的高度,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
测量方法:如图2,人眼在点观察所测物体最高点,量角器零刻度线上两点均在视线上,将铅锤悬挂在量角器的中心点.当铅锤静止时,测得视线与铅垂线所夹的角为,且此时的仰角为.
实践操作:如图3,小明利用上述工具测量河对岸垂直于水平地面的大楼的高度.他先站在水平地面的点处,视线为,此时测角仪上视线与铅垂线的夹角为;然后他向前走10米靠近大楼站在水平地面的点处,视线为,此时测角仪上视线与铅垂线的夹角为.
问题解决:
(1)请用含的代数式表示仰角;
(2)如果在同一平面内,小明的眼睛到水平地面的距离为1.6米,求大楼的高度.(结果保留根号)
22.在菱形中,,点在射线上,连接、.
(1)如图,当点是边的中点,求的正切值;
(2)如图,当点在线段的延长线上,连接与边交于点,如果,的面积等于,求的长;
(3)当点在边上,与交于点,连接并延长与的延长线交于点,如果,△BCH与以点、、所组成的三角形相似,求的长.
23.在直角梯形中,,的平分线交边于点E,点F在线段上,射线与梯形的边相交于点G.
(1)如图1,如果点G与A重合,当时,求的长;
(2)如图2,如果点G在边上,联结,当,且△CGB∽△BAG时,求的值;
(3)当F是中点,且时,求的长.
24.如图1,梯形中,,,.一个动点从点出发,以每秒个单位长度的速度沿线段方向运动,过点作,交折线段于点,以为边向右作正方形,点在射线上,当点到达点时,运动结束.设点的运动时间为秒().
(1)在整个运动过程中,设正方形与△的重合部分面积为,请直接写出与之间的函数关系式和相应的自变量的取值范围;
(2)如图2,当点在线段上运动时,线段与对角线交于点,将△沿翻折,得到△,连接.是否存在这样的,使△是等腰三角形?若存在,求出对应的的值;若不存在,请说明理由.
答案
一、单选题
1.D
【分析】利用锐角三角函数的增减性分类讨论,即可得到答案.
【解析】解:当时,,
,
,
;
当时,,
,
,
;
当,,
,
,
,
综上所述,与的差不能确定,
故选:D.
2.B
【分析】此题根据题意作图根据锐角三角函数表示出AC,再表示出CD即可求出结果.
【解析】解:根据题意作图如下:
由题意知:AB=m,∠A=,
∴,
∴,
即,
故选:B.
3.B
【分析】根据折叠性质得到AF=AD=4,∠DAE=∠FAE=15°,∠D=∠AFE=90°,进而得到∠AFB=30°,解Rt△ABF,求出,进而求出CF=,求出∠EFC=60°,解Rt△CEF,即可求解.
【解析】解:∵四边形ABCD是矩形,
∴∠DAB=∠B=∠C=∠D=90°,AD=BC=4,
由折叠可知,AF=AD=4,∠DAE=∠FAE=15°,∠D=∠AFE=90°,
∴∠BAF=∠BAD-∠DAE∠FAE=60°,
∵∠B=90°,
∴∠AFB=30°,
∴,
∴CF=BC-BF=,
∵∠AFB=30°,∠AFE=90°,
∴∠EFC=60°,
∴在Rt△CEF中,.
故选:B
4.A
【分析】过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,再求出EF即BG的长;在Rt△CBG中求出CG的长,根据CD=CG+GE-DE即可求出宣传牌的高度.
【解析】解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF==,AB=26米,
∴BF=10(米),AF=24(米),
∴BG=AF+AE=54(米),
Rt△BGC中,∠CBG=43°,
∴CG=BG tan43°≈54×0.93=50.22(米),
Rt△ADE中,∠DAE=60°,AE=30米,
∴DE=AE=30(米),
∴CD=CG+GE-DE=50.22+10-30≈8.3(米).
故选:A.
5.B
【分析】本题考查相似三角形的判定与性质、正方形的性质,解题关键是明确题意,找出所求问题需要的条件.
作于,设正方形的边长为,证明,根据相似三角形的性质得,根据锐角三角函数的定义得,求出,表示出正方形和△ABC的面积,即可求解.
【解析】解:作于,设正方形的边长为,
四边形是正方形,
,
,,
,
,
,
,
,
,
,
设,
在中,,
,
∵
,
,
,
,
.
故选:B.
6.B
【分析】作DM⊥CE,根据折叠的性质得∠ACE=∠ACB,BC=EC,然后结合已知条件求出DM和EM的长度,最后在Rt△EDM中运用勾股定理求解即可.
【解析】如图所示,作DM⊥CE于M点,
∵∠ABC=90°,,
∴,则∠CAB=30°,
∵∠ABC=∠BCD=90°,
∴CD∥AB,
∴∠ACD=∠CAB=30°,
根据折叠的性质得:∠ACE=∠ACB=60°,,
∴∠ECD=30°,
设DM=x,则CD=2x,MC=x,
∴EM=EC-MC=-x,
∵,
∴,
解得:,
经检验,是上述分式方程的解,
∴,,
∴在Rt△EDM中,,
故选:B.
二、填空题
7.
【分析】过E点作EF∥AD,对应边成比例,令AD=CE=8k,则OD=2k,OA=6k,作CH⊥AE于点H,由勾股定理求出AC,在△ACE中用等面积法求出CH,从而得出答案.
【解析】如图,作EF∥AD交BC于点F,
∵AD⊥AE,AD平分∠CAB,
∴O是CD中点, ,
∵CE是△ABC的中线,
∴E为AB中点,,
∵AD=CE,
令AD=CE=8k,则OE=OC=4k=EF,OD=2k,OA=6k,
在Rt△ACO中,AC=,
∵AO垂直平分CE,
∴AC=AE=;
过C点作AH⊥AE交AE于点H,
在△ACE中,通过等面积法可得:,
∴CH=,
在Rt△ACH中, ;
故答案为:.
8.
【分析】如图,延长交于F,由题意得,,则,由,可得,计算求解即可.
【解析】解:如图,延长交于F,
∵点D是△ABC的重心,
∴,
∵△ABC是等边三角形,
∴,
∴,
∵△ADE和△ABC都是等边三角形,
∴,
∴,
故答案为:.
9.
【分析】此题考查了相似三角形的性质与判定,三角函数和勾股定理,过作于点,构造相似三角形,再通过性质即可求解,解题的关键是熟练掌握以上知识点的应用.
【解析】如图,过作于点,
在中,由勾股定理得:
∵△ABC与相似,,,
∴,即,
∴,
在中,,
∴,,
在中,由勾股定理得:,
∵,
∴,
∴,
∴,
∴.
10.
【分析】作于点,作于点.则,设,,则,,即可利用表示出的长,在直角中利用勾股定理求得的值,进而求得,得到的长.
【解析】解:作于点,作于点.则.
,
.
设,,则,,
在直角△中,,
则,
,
,
,
,
.
则,
解得:.
又中,
即,
解得:,
则,.
故答案是:.
11.
【分析】由旋转的性质证明是等边三角形和得:AD=DE=AE=5,CE=BD=6,过点E作EH⊥CD,垂足为H.设DH=x,则CH=4-x.由勾股定理得出 62-(4-x)2=52-x2,求出DH,CH的长,由锐角三角函数的定义可得出答案.
【解析】解:∵△ABC是等边三角形
∴AB=AC,
∵绕点逆时针旋转,且与重合,
∴ ,AD=AE
∴是等边三角形,
∴,
∵
∴
又AB=AC,AD=AE
∴
∴
过点作,垂足为.
设,则.
由勾股定理得:,
即,
解得:,
,
故答案为:
12.
【分析】根据题意可得,AC=1200m,,,,,,如图所述,过点作于点,在中,根据正切的计算方法可求出的值,在中根据角的正切值可求出的值,由此即可求解.
【解析】解:根据题意可得,AC=1200m,,,,,,
∴如图所述,过点作于点,
∵,即,且,,
∴,
∴四边形是矩形,即,,
在,AC=1200m,,
∴,则,
∴,
在中,,,
∴,则,
∴,
故答案为:.
13.或
【分析】分两种情况:①当点A在上时:连接作于H,证明得到即可得到答案;②当点A在延长线上时:过点作轴,连接,根据对顶角相等和旋转的性质得出,再根据勾股定理求出,根据30度所对的直角边等于斜边的一半得出,然后利用勾股定理求得即可得出答案.
【解析】解:①当点A在上时:
连接作于H,如图所示,
由题意知:
则
由旋转的性质可知,
在△AOB和中
∴点的坐标为
②当点A在延长线上时:
过点作轴,连接,如图
由①知,
由旋转可知,
,
,
故答案为:或.
14.
【分析】本题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识点,利用已知条件通过添加辅助线构造全等三角形是解题的关键.延长交于点A′,过点F作于H,易证,得出;利用勾股定理求出的长,进而得出.利用互余角的三角函数的关系,得出,在和中利用的值列出方程,即可求得结论.
【解析】解:延长交于点A′,过点F作于H,
∵是正方形,
∴,
∴.
在和中,
.
∴.
∴.
∵E为边的中点,
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵,
∴.
设,则.
∴.
在中,,
∴.
在中, ,
∴.
∴.
∴.
故答案为:.
15.或.
【分析】本题考查了相似三角形的判定和性质,锐角三角函数,勾股定理,利用分类讨论思想解决问题是本题的关键.分两种情况讨论,由相似三角形的性质和锐角三角函数可求解
【解析】当时,如图,过点D作于H,
在中,,,,
∴,
∵,,
∴,
又∵,
∴,
∵,
∴,
∴,
当时,
∵,,
∴,
又∵,
∴,
∴,
∴,
∴,
综上所述:或;
16.3
【分析】由旋转、菱形的性质可知,,则,,,,根据E到直线的距离为,计算求解即可.
【解析】解:如图,菱形绕着点D逆时针旋转后为菱形,
由旋转、菱形的性质可知,,
∴,,
∴,
∴∠BDE=∠ADB-∠ADE=30°,
∴到直线的距离为.
故答案为:3.
17.
【分析】本题主要考查了旋转变化,解直角三角形,求点的运动轨迹,熟练掌握性质定理是解题的关键.根据旋转角度画出图形,在变化的过程中,Q点从点运动到与垂直时,与的交点处,进行计算即可得到答案.
【解析】解:当从到的变化过程中,如图所示,
,
,
当时,点从点开始向方向运动,
当时,的移动到最大距离,
此时,
在中,,
,
,
当时,点开始离开点向点方向运动,
当时,点停止运动,
在中,,
,
点返回运动的路径长为,
点Q移动的路径长为,
故答案为:.
18.
【分析】本题考查了等腰直角三角形的性质,等边三角形的性质,三角形重心的性质,解直角三角形,勾股定理,直角三角形的性质,相似三角形的判定和性质,连接并延长交于,连接,连接并延长交于,由点是的重心,可得分别为的中点,进而由是等边三角形可得,,,设,则,解得,又证明得是等腰直角三角形,得到,点四点共线,即得平分,平分,延长交于,则垂直平分,由勾股定理可得,由直角三角形斜边上的中线等于斜边的一半可得,,得到,根据点在形内,,可得,得到,又根据可得,由,,即可求出线段的取值范围,正确作出辅助线是解题的关键.
【解析】解:如图,连接并延长交于,连接,连接并延长交于,
∵点是的重心,
∴分别为的中点,
∵是等边三角形,
∴,,,
设,则,
在中,,
∴,
∵,
∴,
∵是等腰直角三角形,
∴是等腰直角三角形,
∴,
∴点四点共线,
∴平分,平分,
延长交于,则垂直平分,
∵,,
∴,
∴,
同理可得,
∴,
在中,,
∴,
∵点在形内,
∴,
∴,
∴,
又∵,
∴,
∵,,
∴,
∴,
故答案为:.
三、解答题
19.(1)证明:矩形,
,
,
四边形是平行四边形,
,
是的中线,
,
,
是的中线,
点是的重心;
(2)解:点是的重心,
,
,,
,
,
∵∠ABE=90°,,
,
,
在中,,
.
20.(1)证明:∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(2)过点M作于点H,如图所示:
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
即.
21.(1)解:如图:延长交于L,
由题意得:
∴,
∵,
∴
∴;
(2)解:延长交于点M,
由题意得:,
设米,
在中,,
∴(米),
在中,,
∴(米),
∵,
∴
解得:
∴米,
∴米,
∴大楼EF的高度为米.
22.(1)解:连接,
∵四边形是菱形,
∴,,
∵,
∴是等边三角形,
∵点是边的中点,
∴,,
∴,
又,
∴,
设,
∴,,
在中,,
∴的正切值是.
(2)解:取的中点M,连接,
由(1)可知:,,
∵,
∴,
∴
由勾股定理得:,
∵,
∴,
∵的面积等于
∴
∵与是同高的,设这个高为
,
∴,
∵,
∴,
∴,
∴
在中,,
∴ ,
∴.
(3)过作点,垂足为
由(1)得:是等边三角形,
∴,
∵,
∴,,
∴
∵,
∴,
∵△BCH与以点、G、组成的三角形相似
∴点只能与点G对应,
∴,
∴,
∴,
设,则,
在中,,
∴,
∵,
∴
∵,
∴,
∴,
解得:,(舍去,
∴.
23.(1)解:过点作于点,如图,
∵,
∴,
∵,
∴四边形为矩形,
,
,
,
,
,
∵AD∥BC
∵∠ADE=∠CDE,
,
;
(2)过点作于点,如图,
由(1)知:,
,
,
∵△CGB∽△BAG,
为等腰直角三角形,
(3)①当点在上时,如图,
由(1)知:,
∵是中点,
在和中,
,
,
∵AG=1,ADF=6,
∴,
∴;
②当点在上时,连接,延长,交于点,如图,
由(1)知:,
∵是中点,
∴,
∴为的垂直平分线,
∴,
∴,
∴,
∴,
∴,
∵,
∴△ANG∽△BCG,
∴,
∴,
在和中,
∴,
∴,
设,
则,,
∴,
∴,
∴,
综上,的长为5或.
24.(1)解:如图所示,作于点,于点,设与,交于点,
∴四边形是矩形,
∴,,
∵梯形中,,,
∴,
∴,
∴,
在中,,
∴,,
在中,,
在中,,
∴当时,点和点重合,
第一种情况,当时,,
在中,
∵,
∴,
在中,
∵,
∴,则,
∴,
∵,
∴,
∴,
∴,即,
∴,
∴
;
当正方形的边恰好经过点时,点于点重合,则此时,如图所示,
∴,,
∴,即秒时点与点重合,
第二种情况,当时,,如图所示,
∴由上述证明可得,,
∴,
∴,
∴
;
当点与点重合时,如图所示,
∵,
∴,
第三种情况,当时,如图所示,,
∴,,,
∴,,
∴,
∴,
∵,
∴,
∴
;
当点与点重合时,如图所示,
∴,
第四种情况,当时,如图所示,,
∴,,,
∴
;
综上所述,与之间的函数关系式和相应的自变量的取值范围为
;
(2)解:∵,
∴,
∴由(1)可知,,且,
∴,
第一种情况,当时,如图所示,
∴,
解得,;
第二种情况,当时,如图所示,作于点,
∴,
∵,
∴,
∴,
解得,;
第三种情况,当时,如图所示,作于点,
∴,
∵,
∴,
∴,
解得,;
综上所述,当或或时,△PEF是等腰三角形.
一、单选题
1.如果,那么与的差( ).
A.大于 B.小于 C.等于 D.不能确定
2.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
3.如图,在矩形中,为边上一点,将沿直线翻折,使得点的对应点落在边上.若,则的长度是( )
A. B. C. D.1
4.如图,某大楼DE楼顶挂着“众志成城,抗击疫情”的大型宣传牌,为了测量宣传牌的高度CD,小江从楼底点E向前行走30米到达点A,在A处测得宣传牌下端D的仰角为60°.小江再沿斜坡AB行走26米到达点B,在点B测得宣传牌的上端C的仰角为43°,已知斜坡AB的坡度i=1:2.4,点A、B、C、D、E在同一平面内,CD⊥AE,宣传牌CD的高度约为( )(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,≈1.73)
A.8.3米 B.8.5米 C.8.7米 D.8.9米
5.如图,在等腰三角形中.,.点D,E在边上,点F,G分别在和边上.若四边形为正方形,则( )
A. B. C. D.
6.如图,在四边形ABCD中,∠ABC=∠BCD=90°,,把沿着AC翻折得到,若,则线段DE的长度( )
A. B. C. D.
二、填空题
7.如图,AD是△ABC的角平分线,过点C作AD的垂线交边AB于点E,垂足为点 O,当CE为△ABC边AB上的中线,且CE=AD时,则 .
8.如图,△ABC和△ADE都是等边三角形,点D是△ABC的重心,那么 .
9.如图,已知△ABC与相似,,,,,连接,交边于点,那么线段的长是 .
10.如图,△ABC中,,,,将三角形绕着点A旋转,点C落在直线AB上的点处,点B落在点处,若C、B、恰好在一直线上,则AB的长为 .
11.如图,在等边△ABC内有一点,,,,将绕点逆时针旋转,使与重合,点旋转至点,则的余弦值为 .
12.如图,某飞机于空中处探测到某地面目标在点处,此时飞行高度米,从飞机上看到点的俯角为飞机保持飞行高度不变,且与地面目标分别在两条平行直线上同向运动.当飞机飞行米到达点时,地面目标此时运动到点处,从点看到点的仰角为,则地面目标运动的距离约为 米.(参考数据:)
13.如图,平面直角坐标系中,矩形的顶点,将矩形绕点O顺时针方向旋转,使点A恰好落在直线上的点处,则点B的对应点的坐标为 .
14.如图,正方形中,,为边的中点,点在上,过点作,分别交边、于点、.连接,如果是以为底边的等腰三角形,那么 .
15.定义:如果三角形有两个内角的差为,那么这样的三角形叫做准直角三角形.已知在直角中,,,,如图,如果点在边上,且是准直角三角形,那么 .
16.如图,在菱形中,,,如果将菱形绕着点逆时针旋转后,点恰好落在菱形的初始边上的点处,那么点到直线的距离为 .
17.如图1,含和角的两块三角板和叠合在一起,边与重合,cm,点为边的中点,边与相交于点,现将三角板绕点按逆时针方向旋转角度(如图2),设边与相交于点Q,则当从到的变化过程中,点Q移动的路径长为 .
18.如图,是等腰直角三角形,,,点分别在边上,且,已知是等边三角形,且点在形内,点是的重心,那么线段的取值范围是 .
三、解答题
19.如图,已知是矩形的对角线,,交延长线于,交于,交于.
(1)求证:点是的重心;
(2)如果,求的正弦值.
20.如图,在中,,,垂足为点D,,垂足为点,和相交于点.过点A作,交边延长线于点,点是边上一点,.
(1)求证:;
(2)求证:.
21.小明为测量河对岸大楼的高度,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
测量方法:如图2,人眼在点观察所测物体最高点,量角器零刻度线上两点均在视线上,将铅锤悬挂在量角器的中心点.当铅锤静止时,测得视线与铅垂线所夹的角为,且此时的仰角为.
实践操作:如图3,小明利用上述工具测量河对岸垂直于水平地面的大楼的高度.他先站在水平地面的点处,视线为,此时测角仪上视线与铅垂线的夹角为;然后他向前走10米靠近大楼站在水平地面的点处,视线为,此时测角仪上视线与铅垂线的夹角为.
问题解决:
(1)请用含的代数式表示仰角;
(2)如果在同一平面内,小明的眼睛到水平地面的距离为1.6米,求大楼的高度.(结果保留根号)
22.在菱形中,,点在射线上,连接、.
(1)如图,当点是边的中点,求的正切值;
(2)如图,当点在线段的延长线上,连接与边交于点,如果,的面积等于,求的长;
(3)当点在边上,与交于点,连接并延长与的延长线交于点,如果,△BCH与以点、、所组成的三角形相似,求的长.
23.在直角梯形中,,的平分线交边于点E,点F在线段上,射线与梯形的边相交于点G.
(1)如图1,如果点G与A重合,当时,求的长;
(2)如图2,如果点G在边上,联结,当,且△CGB∽△BAG时,求的值;
(3)当F是中点,且时,求的长.
24.如图1,梯形中,,,.一个动点从点出发,以每秒个单位长度的速度沿线段方向运动,过点作,交折线段于点,以为边向右作正方形,点在射线上,当点到达点时,运动结束.设点的运动时间为秒().
(1)在整个运动过程中,设正方形与△的重合部分面积为,请直接写出与之间的函数关系式和相应的自变量的取值范围;
(2)如图2,当点在线段上运动时,线段与对角线交于点,将△沿翻折,得到△,连接.是否存在这样的,使△是等腰三角形?若存在,求出对应的的值;若不存在,请说明理由.
答案
一、单选题
1.D
【分析】利用锐角三角函数的增减性分类讨论,即可得到答案.
【解析】解:当时,,
,
,
;
当时,,
,
,
;
当,,
,
,
,
综上所述,与的差不能确定,
故选:D.
2.B
【分析】此题根据题意作图根据锐角三角函数表示出AC,再表示出CD即可求出结果.
【解析】解:根据题意作图如下:
由题意知:AB=m,∠A=,
∴,
∴,
即,
故选:B.
3.B
【分析】根据折叠性质得到AF=AD=4,∠DAE=∠FAE=15°,∠D=∠AFE=90°,进而得到∠AFB=30°,解Rt△ABF,求出,进而求出CF=,求出∠EFC=60°,解Rt△CEF,即可求解.
【解析】解:∵四边形ABCD是矩形,
∴∠DAB=∠B=∠C=∠D=90°,AD=BC=4,
由折叠可知,AF=AD=4,∠DAE=∠FAE=15°,∠D=∠AFE=90°,
∴∠BAF=∠BAD-∠DAE∠FAE=60°,
∵∠B=90°,
∴∠AFB=30°,
∴,
∴CF=BC-BF=,
∵∠AFB=30°,∠AFE=90°,
∴∠EFC=60°,
∴在Rt△CEF中,.
故选:B
4.A
【分析】过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,再求出EF即BG的长;在Rt△CBG中求出CG的长,根据CD=CG+GE-DE即可求出宣传牌的高度.
【解析】解:过B作BF⊥AE,交EA的延长线于F,作BG⊥DE于G.
Rt△ABF中,i=tan∠BAF==,AB=26米,
∴BF=10(米),AF=24(米),
∴BG=AF+AE=54(米),
Rt△BGC中,∠CBG=43°,
∴CG=BG tan43°≈54×0.93=50.22(米),
Rt△ADE中,∠DAE=60°,AE=30米,
∴DE=AE=30(米),
∴CD=CG+GE-DE=50.22+10-30≈8.3(米).
故选:A.
5.B
【分析】本题考查相似三角形的判定与性质、正方形的性质,解题关键是明确题意,找出所求问题需要的条件.
作于,设正方形的边长为,证明,根据相似三角形的性质得,根据锐角三角函数的定义得,求出,表示出正方形和△ABC的面积,即可求解.
【解析】解:作于,设正方形的边长为,
四边形是正方形,
,
,,
,
,
,
,
,
,
,
设,
在中,,
,
∵
,
,
,
,
.
故选:B.
6.B
【分析】作DM⊥CE,根据折叠的性质得∠ACE=∠ACB,BC=EC,然后结合已知条件求出DM和EM的长度,最后在Rt△EDM中运用勾股定理求解即可.
【解析】如图所示,作DM⊥CE于M点,
∵∠ABC=90°,,
∴,则∠CAB=30°,
∵∠ABC=∠BCD=90°,
∴CD∥AB,
∴∠ACD=∠CAB=30°,
根据折叠的性质得:∠ACE=∠ACB=60°,,
∴∠ECD=30°,
设DM=x,则CD=2x,MC=x,
∴EM=EC-MC=-x,
∵,
∴,
解得:,
经检验,是上述分式方程的解,
∴,,
∴在Rt△EDM中,,
故选:B.
二、填空题
7.
【分析】过E点作EF∥AD,对应边成比例,令AD=CE=8k,则OD=2k,OA=6k,作CH⊥AE于点H,由勾股定理求出AC,在△ACE中用等面积法求出CH,从而得出答案.
【解析】如图,作EF∥AD交BC于点F,
∵AD⊥AE,AD平分∠CAB,
∴O是CD中点, ,
∵CE是△ABC的中线,
∴E为AB中点,,
∵AD=CE,
令AD=CE=8k,则OE=OC=4k=EF,OD=2k,OA=6k,
在Rt△ACO中,AC=,
∵AO垂直平分CE,
∴AC=AE=;
过C点作AH⊥AE交AE于点H,
在△ACE中,通过等面积法可得:,
∴CH=,
在Rt△ACH中, ;
故答案为:.
8.
【分析】如图,延长交于F,由题意得,,则,由,可得,计算求解即可.
【解析】解:如图,延长交于F,
∵点D是△ABC的重心,
∴,
∵△ABC是等边三角形,
∴,
∴,
∵△ADE和△ABC都是等边三角形,
∴,
∴,
故答案为:.
9.
【分析】此题考查了相似三角形的性质与判定,三角函数和勾股定理,过作于点,构造相似三角形,再通过性质即可求解,解题的关键是熟练掌握以上知识点的应用.
【解析】如图,过作于点,
在中,由勾股定理得:
∵△ABC与相似,,,
∴,即,
∴,
在中,,
∴,,
在中,由勾股定理得:,
∵,
∴,
∴,
∴,
∴.
10.
【分析】作于点,作于点.则,设,,则,,即可利用表示出的长,在直角中利用勾股定理求得的值,进而求得,得到的长.
【解析】解:作于点,作于点.则.
,
.
设,,则,,
在直角△中,,
则,
,
,
,
,
.
则,
解得:.
又中,
即,
解得:,
则,.
故答案是:.
11.
【分析】由旋转的性质证明是等边三角形和得:AD=DE=AE=5,CE=BD=6,过点E作EH⊥CD,垂足为H.设DH=x,则CH=4-x.由勾股定理得出 62-(4-x)2=52-x2,求出DH,CH的长,由锐角三角函数的定义可得出答案.
【解析】解:∵△ABC是等边三角形
∴AB=AC,
∵绕点逆时针旋转,且与重合,
∴ ,AD=AE
∴是等边三角形,
∴,
∵
∴
又AB=AC,AD=AE
∴
∴
过点作,垂足为.
设,则.
由勾股定理得:,
即,
解得:,
,
故答案为:
12.
【分析】根据题意可得,AC=1200m,,,,,,如图所述,过点作于点,在中,根据正切的计算方法可求出的值,在中根据角的正切值可求出的值,由此即可求解.
【解析】解:根据题意可得,AC=1200m,,,,,,
∴如图所述,过点作于点,
∵,即,且,,
∴,
∴四边形是矩形,即,,
在,AC=1200m,,
∴,则,
∴,
在中,,,
∴,则,
∴,
故答案为:.
13.或
【分析】分两种情况:①当点A在上时:连接作于H,证明得到即可得到答案;②当点A在延长线上时:过点作轴,连接,根据对顶角相等和旋转的性质得出,再根据勾股定理求出,根据30度所对的直角边等于斜边的一半得出,然后利用勾股定理求得即可得出答案.
【解析】解:①当点A在上时:
连接作于H,如图所示,
由题意知:
则
由旋转的性质可知,
在△AOB和中
∴点的坐标为
②当点A在延长线上时:
过点作轴,连接,如图
由①知,
由旋转可知,
,
,
故答案为:或.
14.
【分析】本题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识点,利用已知条件通过添加辅助线构造全等三角形是解题的关键.延长交于点A′,过点F作于H,易证,得出;利用勾股定理求出的长,进而得出.利用互余角的三角函数的关系,得出,在和中利用的值列出方程,即可求得结论.
【解析】解:延长交于点A′,过点F作于H,
∵是正方形,
∴,
∴.
在和中,
.
∴.
∴.
∵E为边的中点,
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∵,
∴.
设,则.
∴.
在中,,
∴.
在中, ,
∴.
∴.
∴.
故答案为:.
15.或.
【分析】本题考查了相似三角形的判定和性质,锐角三角函数,勾股定理,利用分类讨论思想解决问题是本题的关键.分两种情况讨论,由相似三角形的性质和锐角三角函数可求解
【解析】当时,如图,过点D作于H,
在中,,,,
∴,
∵,,
∴,
又∵,
∴,
∵,
∴,
∴,
当时,
∵,,
∴,
又∵,
∴,
∴,
∴,
∴,
综上所述:或;
16.3
【分析】由旋转、菱形的性质可知,,则,,,,根据E到直线的距离为,计算求解即可.
【解析】解:如图,菱形绕着点D逆时针旋转后为菱形,
由旋转、菱形的性质可知,,
∴,,
∴,
∴∠BDE=∠ADB-∠ADE=30°,
∴到直线的距离为.
故答案为:3.
17.
【分析】本题主要考查了旋转变化,解直角三角形,求点的运动轨迹,熟练掌握性质定理是解题的关键.根据旋转角度画出图形,在变化的过程中,Q点从点运动到与垂直时,与的交点处,进行计算即可得到答案.
【解析】解:当从到的变化过程中,如图所示,
,
,
当时,点从点开始向方向运动,
当时,的移动到最大距离,
此时,
在中,,
,
,
当时,点开始离开点向点方向运动,
当时,点停止运动,
在中,,
,
点返回运动的路径长为,
点Q移动的路径长为,
故答案为:.
18.
【分析】本题考查了等腰直角三角形的性质,等边三角形的性质,三角形重心的性质,解直角三角形,勾股定理,直角三角形的性质,相似三角形的判定和性质,连接并延长交于,连接,连接并延长交于,由点是的重心,可得分别为的中点,进而由是等边三角形可得,,,设,则,解得,又证明得是等腰直角三角形,得到,点四点共线,即得平分,平分,延长交于,则垂直平分,由勾股定理可得,由直角三角形斜边上的中线等于斜边的一半可得,,得到,根据点在形内,,可得,得到,又根据可得,由,,即可求出线段的取值范围,正确作出辅助线是解题的关键.
【解析】解:如图,连接并延长交于,连接,连接并延长交于,
∵点是的重心,
∴分别为的中点,
∵是等边三角形,
∴,,,
设,则,
在中,,
∴,
∵,
∴,
∵是等腰直角三角形,
∴是等腰直角三角形,
∴,
∴点四点共线,
∴平分,平分,
延长交于,则垂直平分,
∵,,
∴,
∴,
同理可得,
∴,
在中,,
∴,
∵点在形内,
∴,
∴,
∴,
又∵,
∴,
∵,,
∴,
∴,
故答案为:.
三、解答题
19.(1)证明:矩形,
,
,
四边形是平行四边形,
,
是的中线,
,
,
是的中线,
点是的重心;
(2)解:点是的重心,
,
,,
,
,
∵∠ABE=90°,,
,
,
在中,,
.
20.(1)证明:∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(2)过点M作于点H,如图所示:
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
即.
21.(1)解:如图:延长交于L,
由题意得:
∴,
∵,
∴
∴;
(2)解:延长交于点M,
由题意得:,
设米,
在中,,
∴(米),
在中,,
∴(米),
∵,
∴
解得:
∴米,
∴米,
∴大楼EF的高度为米.
22.(1)解:连接,
∵四边形是菱形,
∴,,
∵,
∴是等边三角形,
∵点是边的中点,
∴,,
∴,
又,
∴,
设,
∴,,
在中,,
∴的正切值是.
(2)解:取的中点M,连接,
由(1)可知:,,
∵,
∴,
∴
由勾股定理得:,
∵,
∴,
∵的面积等于
∴
∵与是同高的,设这个高为
,
∴,
∵,
∴,
∴,
∴
在中,,
∴ ,
∴.
(3)过作点,垂足为
由(1)得:是等边三角形,
∴,
∵,
∴,,
∴
∵,
∴,
∵△BCH与以点、G、组成的三角形相似
∴点只能与点G对应,
∴,
∴,
∴,
设,则,
在中,,
∴,
∵,
∴
∵,
∴,
∴,
解得:,(舍去,
∴.
23.(1)解:过点作于点,如图,
∵,
∴,
∵,
∴四边形为矩形,
,
,
,
,
,
∵AD∥BC
∵∠ADE=∠CDE,
,
;
(2)过点作于点,如图,
由(1)知:,
,
,
∵△CGB∽△BAG,
为等腰直角三角形,
(3)①当点在上时,如图,
由(1)知:,
∵是中点,
在和中,
,
,
∵AG=1,ADF=6,
∴,
∴;
②当点在上时,连接,延长,交于点,如图,
由(1)知:,
∵是中点,
∴,
∴为的垂直平分线,
∴,
∴,
∴,
∴,
∴,
∵,
∴△ANG∽△BCG,
∴,
∴,
在和中,
∴,
∴,
设,
则,,
∴,
∴,
∴,
综上,的长为5或.
24.(1)解:如图所示,作于点,于点,设与,交于点,
∴四边形是矩形,
∴,,
∵梯形中,,,
∴,
∴,
∴,
在中,,
∴,,
在中,,
在中,,
∴当时,点和点重合,
第一种情况,当时,,
在中,
∵,
∴,
在中,
∵,
∴,则,
∴,
∵,
∴,
∴,
∴,即,
∴,
∴
;
当正方形的边恰好经过点时,点于点重合,则此时,如图所示,
∴,,
∴,即秒时点与点重合,
第二种情况,当时,,如图所示,
∴由上述证明可得,,
∴,
∴,
∴
;
当点与点重合时,如图所示,
∵,
∴,
第三种情况,当时,如图所示,,
∴,,,
∴,,
∴,
∴,
∵,
∴,
∴
;
当点与点重合时,如图所示,
∴,
第四种情况,当时,如图所示,,
∴,,,
∴
;
综上所述,与之间的函数关系式和相应的自变量的取值范围为
;
(2)解:∵,
∴,
∴由(1)可知,,且,
∴,
第一种情况,当时,如图所示,
∴,
解得,;
第二种情况,当时,如图所示,作于点,
∴,
∵,
∴,
∴,
解得,;
第三种情况,当时,如图所示,作于点,
∴,
∵,
∴,
∴,
解得,;
综上所述,当或或时,△PEF是等腰三角形.
