沪教版九年级数学上册 第二十五章《锐角的三角比》单元复习卷(含解析)
文档属性
| 名称 | 沪教版九年级数学上册 第二十五章《锐角的三角比》单元复习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 11:07:27 | ||
图片预览


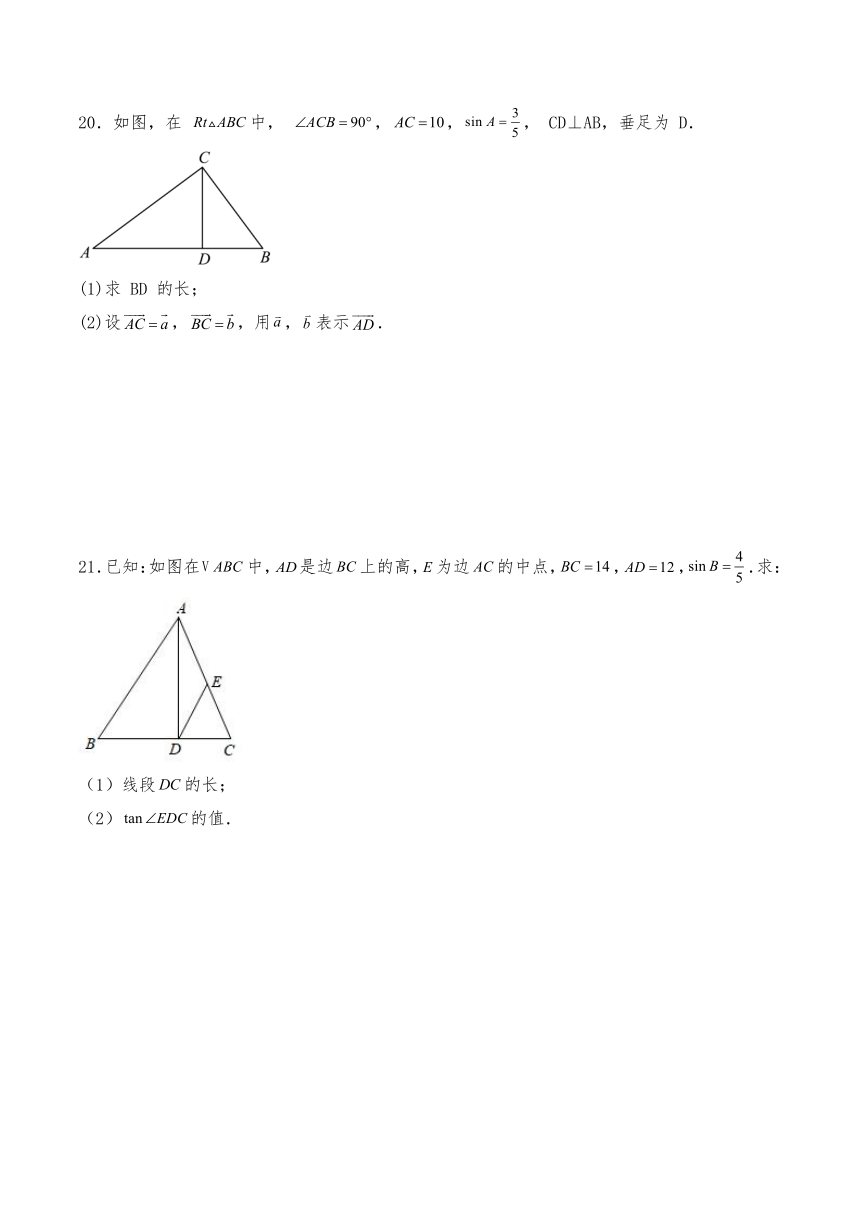

文档简介
第二十五章《锐角的三角比》单元复习卷
一、单选题
1.如果的各边长都缩小为原来的倍,那么锐角A的正弦、余弦值是( )
A.都扩大为原来的2倍 B.都缩小为原来的
C.没有变化 D.不能确定
2.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
3.如果锐角的正切值为,那么下列结论中正确的是( )
A. B. C. D.
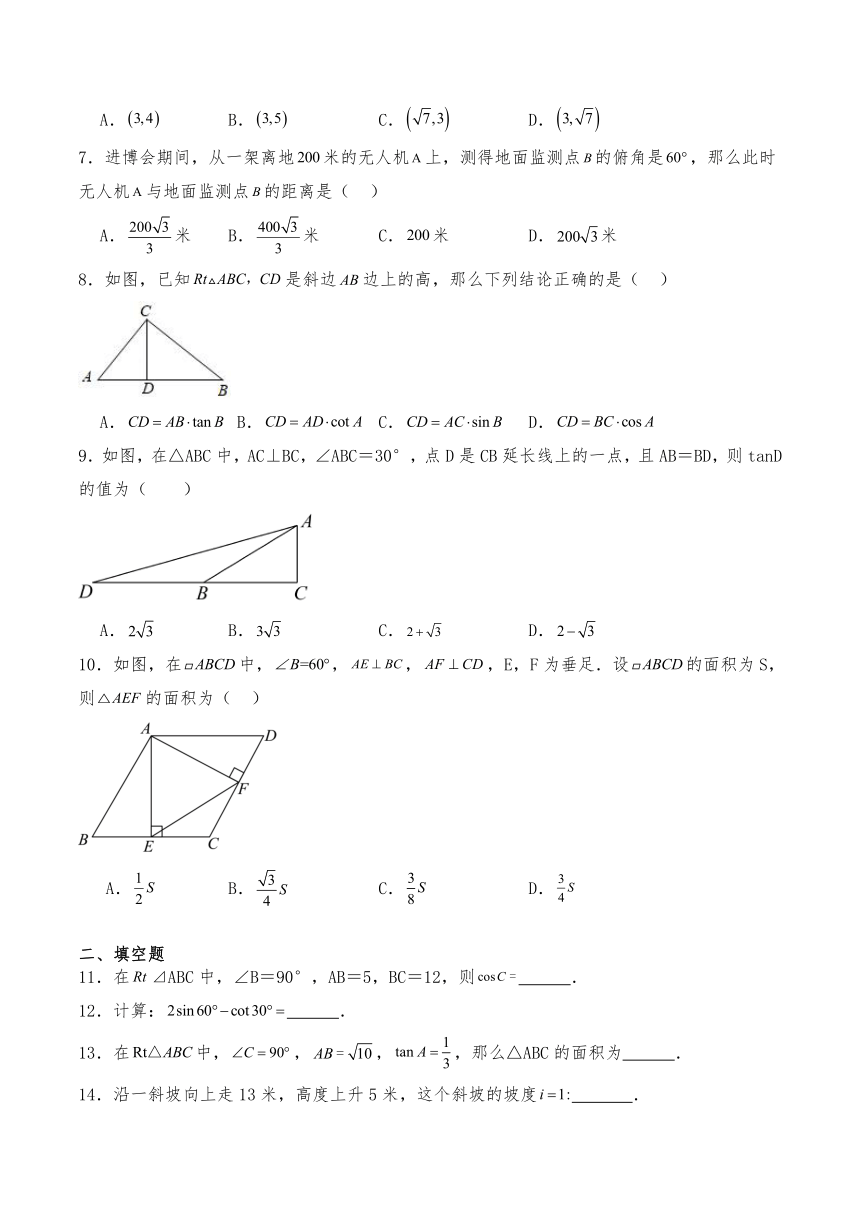
4.在Rt△ABC中,已知,,,那么的长等于 ( )
A.1 B.9 C. D.
5.如图,△ABC的顶点均在正方形网格的格点上,则的值为( )
A. B.2 C. D.
6.如图,在直角坐标平面内,点P与原点O的距离,线段OP与x轴正半轴的夹角为,且,则点P的坐标是( )
A. B. C. D.
7.进博会期间,从一架离地米的无人机上,测得地面监测点的俯角是,那么此时无人机与地面监测点的距离是( )
A.米 B.米 C.米 D.米
8.如图,已知是斜边边上的高,那么下列结论正确的是( )
A. B. C. D.
9.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tanD的值为( )
A. B. C. D.
10.如图,在中,,,,E,F为垂足.设的面积为S,则的面积为( )
A. B. C. D.
二、填空题
11.在⊿ABC中,∠B=90°,AB=5,BC=12,则 .
12.计算: .
13.在中,,,,那么△ABC的面积为 .
14.沿一斜坡向上走13米,高度上升5米,这个斜坡的坡度 .
15.如图,在△ABC中,,,的垂直平分线交于点,那么:的值是 .
16.如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若,则tan∠DEC的值是 .
17.若定义等腰三角形顶角的值为等腰三角形底边和底边上高的比值,即顶角,若等腰△ABC,,且,则 .
18.如图,已知在中,,,,是边 上一点,将沿直线翻折,点落在点处,如果,那么点与点的距离等于 .
三、解答题
19.计算:(1)sin260°-tan30° cos30°+tan45°;
(2).
20.如图,在 中, ,,, CD⊥AB,垂足为 D.
(1)求 BD 的长;
(2)设,,用,表示.
21.已知:如图在中,是边上的高,为边的中点,,,.求:
(1)线段的长;
(2)的值.
22.如图,四边形中,.
(1)如果,求的值;
(2)如果,求四边形的面积.
23.每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处?请说明理由.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
24.已知:如图,第一象限内的点在反比例函数的图像上,点在轴上,轴,点的坐标为,且.求:
(1)反比例函数的解析式;
(2)点的坐标;
(3)的余弦值.
25.如图,已知直线与x轴、y轴交于点A、C,点A与点B关于直线轴对称,点D在直线上,且D在第三象限,.
(1)求证:求点D及直线解析式;
(2)求的正弦值;
(3)如果P是射线上一点,且以点P,A,B为顶点的三角形与相似,求点P的坐标.
26.已知在△ABC中,,(点是边上一点,不与重合,过点作,垂足为点,点是边上一点,连接,以为邻边作平行四边形.
(1)如图1,如果,点恰好在边上,求的余切值;
(2)如图2,如果,点在△ABC内,设,求与的函数关系式,并写出定义域:
(3)在第(2)小题的条件下,如果平行四边形是矩形,求的值.
答案
一、单选题
1.C
【分析】根据相似三角形的判定定理、正弦、余弦的概念解答.
【解析】三角形各边长度都缩小为原来的倍,
∴得到的三角形与原三角形相似,
∴锐角A的大小不变,
∴锐角A的正弦、余弦值不变,
故选:C.
2.A
【分析】根据锐角A的邻边a与对边b的比叫做∠A的余切,记作cotA.
【解析】解:∵∠C=90°,
∴=,
故选:A.
3.C
【分析】利用30度角和45度角的正切值与角的正切值比较,即可得到答案.
【解析】∵,,
而,
∴,
故选:C.
4.A
【分析】本题考查解直角三角形,根据题意,表示出的正切即可解决问题.
【解析】解:在中,
,
又因为,,
所以,
解得.
故选:A.
5.A
【分析】连接小正方形的对角线,证明是直角三角形,再利用正切的定义求解即可.
【解析】如图,连接小正方形的对角线,
设每个小正方形的边长为1,
则由勾股定理得,,
∵,
即,
∴是直角三角形,
∴.
故选:A.
6.D
【分析】根据题意作x轴的垂线,根据,且,从而求出横坐标,再求点P的坐标就容易了.
【解析】过P作x轴的垂线,交x轴于点A,
∵,,
∴,
∴,
∴.
∴点P的坐标是.
故选:D.
7.B
【分析】本题考查了解直角三角形,仰角俯角,熟练掌握锐角三角函数的定义是解答本题的关键.
根据题意,得到,利用已知角的正弦,求出答案.
【解析】解:如图,在中,
米,,
,
(米),
故选:.
8.D
【分析】利用直角三角形的边角间关系,计算得结论.
【解析】解:∵是斜边边上的高,
∴都是直角三角形.
在中,
∵,故选项B不正确;
在中,
∵,故选项A、C不正确.
在中,
∵,
∴.
∴,故选项D正确.
故选:D.
9.D
【分析】设AC=m,解直角三角形求出AB,BC,BD即可解决问题.
【解析】设AC=m,
在Rt△ABC中,∵∠C=90°,∠ABC=30°,
∴AB=2AC=2m,BC=AC=m,
∴BD=AB=2m,DC=2m+m,
∴tan∠ADC===2﹣.
故选:D.
10.C
【分析】过点F作FH⊥AE于H,根据平行四边形的性质可得AD=BC,∠D=∠B=60°,∠BAD=180°-∠B=120°,从而求出∠HAF=60°,然后根据平行四边形的面积公式可得BC·AE=S,利用锐角三角函数求出AF=,FH=,最后根据三角形的面积公式即可求解.
【解析】解:过点F作FH⊥AE于H
∵四边形ABCD为平行四边形,
∴AD=BC,∠D=∠B=60°,∠BAD=180°-∠B=120°
∵,
∴∠BAE=90°-∠B=30°,∠DAF=90°-∠D=30°
∴∠HAF=∠BAD-∠BAE-∠DAF=60°
∵的面积为S,
∴BC·AE=S
在Rt△ADF中,AF=AD·sinD=
在Rt△AHF中,FH=AF·sin∠HAF==
∴S△AEF=AE·FH
=AE·
=·AE
=
故选C.
二、填空题
11.
【分析】根据余弦的定义进行解答
【解析】在Rt△ABC中,AC=,
,故填.
12.
【分析】本题考查了特殊角的三角函数值;根据特殊角的三角函数值进行计算即可求解.
【解析】解:,
故答案为:.
13.
【分析】本题主要考查了解直角三角形,勾股定理,先根据正切的定义得到,再由勾股定理得到,解得,则,再根据三角形面积计算公式求解即可.
【解析】解:如图所示,在中,,,
∴,
由勾股定理得,
∴,
∴(负值舍去),
∴,
∴,
故答案为:.
14.2.4
【分析】根据勾股定理求出此人行走的水平距离,根据坡度的概念计算即可.
【解析】解:由勾股定理得,此人行走的水平距离为:=12,
则此斜坡的坡度i=5:12=1:2.4,
故答案为:2.4.
15.7
【分析】过点A作于,作的垂直平分线交于点、交于,根据余弦的定义求出,根据勾股定理求出,根据平行线分线段成比例定理列出比例式,计算即可.
【解析】解:过点A作于,作的垂直平分线交于点、交于,
在中,,,
则,
解得:,
由勾股定理得:,
在中,,
则,
∴,
是的垂直平分线,
∴,
∴,
∵,,
∴,
∴,
故答案为:.
16.
【分析】过点作于点,易证,从而可求出,,设AB=a,则AD=2a,根据三角形的面积可求出AE,然后根据锐角三角函数的定义即可求出答案.
【解析】解:如图,过点作于点,设,
在与中,
,
,
,,
,tan∠ADB==,
设AB=a,则AD=2a,
∴BD=a,
∵S△ABD=BD AE=AB AD,
∴AE=CF=a,
∴BE=FD=a,
∴EF=BD﹣2BE=a﹣a=a,
∴tan∠DEC==,
故答案为:.
17.
【分析】本题主要考查了等腰三角形的性质,勾股定理以及锐角三角函数的定义,熟练掌握等腰三角形的性质是解题的关键.过点A作于,设,,根据等腰三角形的性质及勾股定理得,即可求得答案.
【解析】解:如图,过点A作于,过点作于,
,
设,则,
,,
,
根据勾股定理得,,
.
故答案为:.
18.
【分析】由题意可得如图所示,过点A作AG⊥BC于点G,过点E作EF⊥AB于点F,则有,然后可得,进而可得,则有,,最后问题可求解.
【解析】解:过点A作AG⊥BC于点G,过点E作EF⊥AB于点F,如图,
∵,,
∴,
∴,
∴,
由折叠的性质可得,
∵,
∴,
∵,
∴(AAS),
∴,,
∴,
∴;
故答案为.
三、解答题
19.解:(1)原式=
=
=.
(2)原式=
=
=-
=-
20.(1)解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△ACD中,,
∴.
∴,
∴.
∵∠ACB=90°,
∴∠DCB+∠B =∠A+∠B=90°,
∴∠DCB=∠A.
∴;
(2)解:∵,
∴,
又∵,
∴.
21.解:(1) 是边上的高,,,
,
∵AB=15,BD= =9,
∴BD=14,
∴CD=BC-BD=14-9=5.
(2) 为边的中点,
∴ED=EA=EC
∴tan∠EDC=tan∠ECD= =
22.(1)解:如图,过点A作于点E,
∵,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∴;
(2)解:如图,过点A作于点E,
∵,
∴,
∴四边形是矩形,
∴,
设,则,
在中,,
∴,
解得:,
即,
四边形的面积.
23.(1)解:在Rt△ABD中,∠ABD=53°,BD=9m,
∴AB==15(m),
∴此时云梯AB的长为15m;
(2)解:在该消防车不移动位置的前提下,云梯能伸到险情处,
理由:由题意得:
DE=BC=2m,
∵AE=19m,
∴AD=AE-DE=19-2=17(m),
在Rt△ABD中,BD=9m,
∴AB= (m),
∵m<20m,
∴在该消防车不移动位置的前提下,云梯能伸到险情处.
24.(1)解:设反比例函数的解析式为,
∵第一象限内的点在反比例函数的图像上,点的坐标为,
∴,
∴反比例函数的解析式为;
(2)解:过A作于D,则,
设,
∵轴,
∴,,
∴,
解得,经检验,符合所列方程,
故点C坐标为;
(3)解:∵轴,
∴点B的纵坐标为1,
将代入中,得,则,
∴,
又,,
∴,
∴.
25.(1)解:直线与轴、轴交于点、,
,,
点与点关于直线轴对称,
,
点在直线上,
设,
,
,
∴或,经检验符合题意;
∵D在第三象限,
.
设直线解析式为y=kx+b(k≠0),
,
,
直线解析式为.
(2)解:过作,连接,
同理可得:直线的解析式为,
当时,则,
∴直线与轴的交点,
,
,
,
∵,,
∴,
中,.
(3)解:如图,
由,可得,
直线的表达式为,
,
即,,
当,则,
∴,
∴,
∴四边形为平行四边形时,
∴;
当,则,
∴,
∵,
∴,
解得,
∴,即,
∴,
.
综上,或.
26.(1)解:在中,,
又,
,
,
,
在中,
,
又,,
,
四边形是平行四边形,
,
点在上,
,
,
,
,
在中,;
(2)解:四边形是平行四边形,
,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
过点E作于H,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
即;
当点恰好在上时,
,
,
∵,则,
,
在中,,
又,则,
,
,
,
,
当点在△ABC内时,;
(3)解:设,则,
,
设矩形的对角线与相交于点,连接,
平行四边形是矩形,
,
,,
,
,
过点作于点,
又,
,
,
,
,
,,
,
.
一、单选题
1.如果的各边长都缩小为原来的倍,那么锐角A的正弦、余弦值是( )
A.都扩大为原来的2倍 B.都缩小为原来的
C.没有变化 D.不能确定
2.在Rt△ABC中,∠C=90 ,那么等于( )
A. B. C. D.
3.如果锐角的正切值为,那么下列结论中正确的是( )
A. B. C. D.
4.在Rt△ABC中,已知,,,那么的长等于 ( )
A.1 B.9 C. D.
5.如图,△ABC的顶点均在正方形网格的格点上,则的值为( )
A. B.2 C. D.
6.如图,在直角坐标平面内,点P与原点O的距离,线段OP与x轴正半轴的夹角为,且,则点P的坐标是( )
A. B. C. D.
7.进博会期间,从一架离地米的无人机上,测得地面监测点的俯角是,那么此时无人机与地面监测点的距离是( )
A.米 B.米 C.米 D.米
8.如图,已知是斜边边上的高,那么下列结论正确的是( )
A. B. C. D.
9.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tanD的值为( )
A. B. C. D.
10.如图,在中,,,,E,F为垂足.设的面积为S,则的面积为( )
A. B. C. D.
二、填空题
11.在⊿ABC中,∠B=90°,AB=5,BC=12,则 .
12.计算: .
13.在中,,,,那么△ABC的面积为 .
14.沿一斜坡向上走13米,高度上升5米,这个斜坡的坡度 .
15.如图,在△ABC中,,,的垂直平分线交于点,那么:的值是 .
16.如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若,则tan∠DEC的值是 .
17.若定义等腰三角形顶角的值为等腰三角形底边和底边上高的比值,即顶角,若等腰△ABC,,且,则 .
18.如图,已知在中,,,,是边 上一点,将沿直线翻折,点落在点处,如果,那么点与点的距离等于 .
三、解答题
19.计算:(1)sin260°-tan30° cos30°+tan45°;
(2).
20.如图,在 中, ,,, CD⊥AB,垂足为 D.
(1)求 BD 的长;
(2)设,,用,表示.
21.已知:如图在中,是边上的高,为边的中点,,,.求:
(1)线段的长;
(2)的值.
22.如图,四边形中,.
(1)如果,求的值;
(2)如果,求四边形的面积.
23.每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处?请说明理由.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
24.已知:如图,第一象限内的点在反比例函数的图像上,点在轴上,轴,点的坐标为,且.求:
(1)反比例函数的解析式;
(2)点的坐标;
(3)的余弦值.
25.如图,已知直线与x轴、y轴交于点A、C,点A与点B关于直线轴对称,点D在直线上,且D在第三象限,.
(1)求证:求点D及直线解析式;
(2)求的正弦值;
(3)如果P是射线上一点,且以点P,A,B为顶点的三角形与相似,求点P的坐标.
26.已知在△ABC中,,(点是边上一点,不与重合,过点作,垂足为点,点是边上一点,连接,以为邻边作平行四边形.
(1)如图1,如果,点恰好在边上,求的余切值;
(2)如图2,如果,点在△ABC内,设,求与的函数关系式,并写出定义域:
(3)在第(2)小题的条件下,如果平行四边形是矩形,求的值.
答案
一、单选题
1.C
【分析】根据相似三角形的判定定理、正弦、余弦的概念解答.
【解析】三角形各边长度都缩小为原来的倍,
∴得到的三角形与原三角形相似,
∴锐角A的大小不变,
∴锐角A的正弦、余弦值不变,
故选:C.
2.A
【分析】根据锐角A的邻边a与对边b的比叫做∠A的余切,记作cotA.
【解析】解:∵∠C=90°,
∴=,
故选:A.
3.C
【分析】利用30度角和45度角的正切值与角的正切值比较,即可得到答案.
【解析】∵,,
而,
∴,
故选:C.
4.A
【分析】本题考查解直角三角形,根据题意,表示出的正切即可解决问题.
【解析】解:在中,
,
又因为,,
所以,
解得.
故选:A.
5.A
【分析】连接小正方形的对角线,证明是直角三角形,再利用正切的定义求解即可.
【解析】如图,连接小正方形的对角线,
设每个小正方形的边长为1,
则由勾股定理得,,
∵,
即,
∴是直角三角形,
∴.
故选:A.
6.D
【分析】根据题意作x轴的垂线,根据,且,从而求出横坐标,再求点P的坐标就容易了.
【解析】过P作x轴的垂线,交x轴于点A,
∵,,
∴,
∴,
∴.
∴点P的坐标是.
故选:D.
7.B
【分析】本题考查了解直角三角形,仰角俯角,熟练掌握锐角三角函数的定义是解答本题的关键.
根据题意,得到,利用已知角的正弦,求出答案.
【解析】解:如图,在中,
米,,
,
(米),
故选:.
8.D
【分析】利用直角三角形的边角间关系,计算得结论.
【解析】解:∵是斜边边上的高,
∴都是直角三角形.
在中,
∵,故选项B不正确;
在中,
∵,故选项A、C不正确.
在中,
∵,
∴.
∴,故选项D正确.
故选:D.
9.D
【分析】设AC=m,解直角三角形求出AB,BC,BD即可解决问题.
【解析】设AC=m,
在Rt△ABC中,∵∠C=90°,∠ABC=30°,
∴AB=2AC=2m,BC=AC=m,
∴BD=AB=2m,DC=2m+m,
∴tan∠ADC===2﹣.
故选:D.
10.C
【分析】过点F作FH⊥AE于H,根据平行四边形的性质可得AD=BC,∠D=∠B=60°,∠BAD=180°-∠B=120°,从而求出∠HAF=60°,然后根据平行四边形的面积公式可得BC·AE=S,利用锐角三角函数求出AF=,FH=,最后根据三角形的面积公式即可求解.
【解析】解:过点F作FH⊥AE于H
∵四边形ABCD为平行四边形,
∴AD=BC,∠D=∠B=60°,∠BAD=180°-∠B=120°
∵,
∴∠BAE=90°-∠B=30°,∠DAF=90°-∠D=30°
∴∠HAF=∠BAD-∠BAE-∠DAF=60°
∵的面积为S,
∴BC·AE=S
在Rt△ADF中,AF=AD·sinD=
在Rt△AHF中,FH=AF·sin∠HAF==
∴S△AEF=AE·FH
=AE·
=·AE
=
故选C.
二、填空题
11.
【分析】根据余弦的定义进行解答
【解析】在Rt△ABC中,AC=,
,故填.
12.
【分析】本题考查了特殊角的三角函数值;根据特殊角的三角函数值进行计算即可求解.
【解析】解:,
故答案为:.
13.
【分析】本题主要考查了解直角三角形,勾股定理,先根据正切的定义得到,再由勾股定理得到,解得,则,再根据三角形面积计算公式求解即可.
【解析】解:如图所示,在中,,,
∴,
由勾股定理得,
∴,
∴(负值舍去),
∴,
∴,
故答案为:.
14.2.4
【分析】根据勾股定理求出此人行走的水平距离,根据坡度的概念计算即可.
【解析】解:由勾股定理得,此人行走的水平距离为:=12,
则此斜坡的坡度i=5:12=1:2.4,
故答案为:2.4.
15.7
【分析】过点A作于,作的垂直平分线交于点、交于,根据余弦的定义求出,根据勾股定理求出,根据平行线分线段成比例定理列出比例式,计算即可.
【解析】解:过点A作于,作的垂直平分线交于点、交于,
在中,,,
则,
解得:,
由勾股定理得:,
在中,,
则,
∴,
是的垂直平分线,
∴,
∴,
∵,,
∴,
∴,
故答案为:.
16.
【分析】过点作于点,易证,从而可求出,,设AB=a,则AD=2a,根据三角形的面积可求出AE,然后根据锐角三角函数的定义即可求出答案.
【解析】解:如图,过点作于点,设,
在与中,
,
,
,,
,tan∠ADB==,
设AB=a,则AD=2a,
∴BD=a,
∵S△ABD=BD AE=AB AD,
∴AE=CF=a,
∴BE=FD=a,
∴EF=BD﹣2BE=a﹣a=a,
∴tan∠DEC==,
故答案为:.
17.
【分析】本题主要考查了等腰三角形的性质,勾股定理以及锐角三角函数的定义,熟练掌握等腰三角形的性质是解题的关键.过点A作于,设,,根据等腰三角形的性质及勾股定理得,即可求得答案.
【解析】解:如图,过点A作于,过点作于,
,
设,则,
,,
,
根据勾股定理得,,
.
故答案为:.
18.
【分析】由题意可得如图所示,过点A作AG⊥BC于点G,过点E作EF⊥AB于点F,则有,然后可得,进而可得,则有,,最后问题可求解.
【解析】解:过点A作AG⊥BC于点G,过点E作EF⊥AB于点F,如图,
∵,,
∴,
∴,
∴,
由折叠的性质可得,
∵,
∴,
∵,
∴(AAS),
∴,,
∴,
∴;
故答案为.
三、解答题
19.解:(1)原式=
=
=.
(2)原式=
=
=-
=-
20.(1)解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△ACD中,,
∴.
∴,
∴.
∵∠ACB=90°,
∴∠DCB+∠B =∠A+∠B=90°,
∴∠DCB=∠A.
∴;
(2)解:∵,
∴,
又∵,
∴.
21.解:(1) 是边上的高,,,
,
∵AB=15,BD= =9,
∴BD=14,
∴CD=BC-BD=14-9=5.
(2) 为边的中点,
∴ED=EA=EC
∴tan∠EDC=tan∠ECD= =
22.(1)解:如图,过点A作于点E,
∵,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∴;
(2)解:如图,过点A作于点E,
∵,
∴,
∴四边形是矩形,
∴,
设,则,
在中,,
∴,
解得:,
即,
四边形的面积.
23.(1)解:在Rt△ABD中,∠ABD=53°,BD=9m,
∴AB==15(m),
∴此时云梯AB的长为15m;
(2)解:在该消防车不移动位置的前提下,云梯能伸到险情处,
理由:由题意得:
DE=BC=2m,
∵AE=19m,
∴AD=AE-DE=19-2=17(m),
在Rt△ABD中,BD=9m,
∴AB= (m),
∵m<20m,
∴在该消防车不移动位置的前提下,云梯能伸到险情处.
24.(1)解:设反比例函数的解析式为,
∵第一象限内的点在反比例函数的图像上,点的坐标为,
∴,
∴反比例函数的解析式为;
(2)解:过A作于D,则,
设,
∵轴,
∴,,
∴,
解得,经检验,符合所列方程,
故点C坐标为;
(3)解:∵轴,
∴点B的纵坐标为1,
将代入中,得,则,
∴,
又,,
∴,
∴.
25.(1)解:直线与轴、轴交于点、,
,,
点与点关于直线轴对称,
,
点在直线上,
设,
,
,
∴或,经检验符合题意;
∵D在第三象限,
.
设直线解析式为y=kx+b(k≠0),
,
,
直线解析式为.
(2)解:过作,连接,
同理可得:直线的解析式为,
当时,则,
∴直线与轴的交点,
,
,
,
∵,,
∴,
中,.
(3)解:如图,
由,可得,
直线的表达式为,
,
即,,
当,则,
∴,
∴,
∴四边形为平行四边形时,
∴;
当,则,
∴,
∵,
∴,
解得,
∴,即,
∴,
.
综上,或.
26.(1)解:在中,,
又,
,
,
,
在中,
,
又,,
,
四边形是平行四边形,
,
点在上,
,
,
,
,
在中,;
(2)解:四边形是平行四边形,
,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
过点E作于H,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
即;
当点恰好在上时,
,
,
∵,则,
,
在中,,
又,则,
,
,
,
,
当点在△ABC内时,;
(3)解:设,则,
,
设矩形的对角线与相交于点,连接,
平行四边形是矩形,
,
,,
,
,
过点作于点,
又,
,
,
,
,
,,
,
.
